基于乘性一致性调整算法的二元语义决策模型①
钱佳燕, 乔青青, 金飞飞, 何莹莹, 杨 丽, 梁翠娴
(安徽大学商学院,安徽 合肥 230601)
0 引 言
在决策环境下,决策者通常要面对的问题是如何在众多的可行备选方案中挑选出一个最优方案,为此,学者们进行了不同方向的研究。近年来,学者们在二元语义方向的研究方法多,研究成果颇丰[1-3]。西班牙Herrera教授[4]2000年在《IEEE Transactions on Fuzzy Systems》上首次提出了采用二元语义描述语言评价信息的方法,这是一个重大突破。先将决策者的评价信息转化为二元语义符号,再进一步处理,可有效避免语言评价信息集结和运算中出现的信息损失和扭曲,也使语义信息计算结果更为精确[5, 6]。目前,在多属性、群决策等方面的研究是基于二元语义决策研究的热点问题。但是,很少有学者将二元语义与乘性一致性结合起来进行研究。针对上述问题,通过构造局部调整的一致性公式,结合迭代法,提出了基于乘性一致性的二元语义模型。需要指出的是,采用二元语义计算模型对语义评价信息进行处理和运算,具有计算方法简单和计算结果更加精确等特点,有广阔的应用前景。
1 预备知识
二元语义信息
定义1.1.1[7]设S={s0,s1,…,s2τ}是一个语义术语集,其中τ是一个正整数,那么集合S具有有序性:若si,sj∈S且i>j,则si>sj。
Herrera和Martinez[4,8]提出了二元语义变量,它是由si和αi组成,其中si∈S={si|i=0,1,…,2τ}为语义术语,αi∈(-0.5,0.5]为决策者给定的评估值与语言项si之间的偏差[4]。
定义1.1.2[4]设S={si|i=0,1,…,2τ}为语义术语集,β∈[0,2τ]为集成运算值,则可以用转换函数Δ将实数β转化为对等的二元语义变量。其中转换函数Δ为:
Δ(β)=(si,ai)
(1)
i=round(β),ai=β-i,
其中,“round”表示取整函数;αi∈(-0.5,0.5]。
反之,总存在一个转换函数的逆函数Δ-1,使得任意的(si,ai)转化为对等的实数β,即:
β=Δ-1(si,ai)=ai+i
(2)
定义1.1.3[9]设(s1,a1),(s2,a2),…,(sn,an)是一列二元语义变量,则二元语义算术平均算子定义如下:
(3)
2 乘性一致性改进算法
2.1 乘性一致语言偏好关系的构造
定理2.1.1假设(sij,aij)是由决策者给出的二元语义信息,如果它满足下列式子,则它同时具有乘性一致性,
Δ-1(sij,aij)=
(4)
对上式的证明:
因此,可得:
故,综上可得:
Δ-1(sij,aij)Δ-1(sjk,ajk)Δ-1(ski,aki)=
Δ-1(sik,aik)Δ-1(skj,akj)Δ-1(sji,aji),∀i,j,k∈N,
即可以得到Δ-1(sij,aij)具有乘性一致性。

(5)

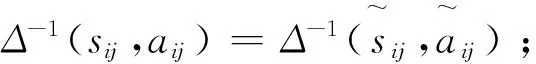
2.2 乘性一致性改进过程
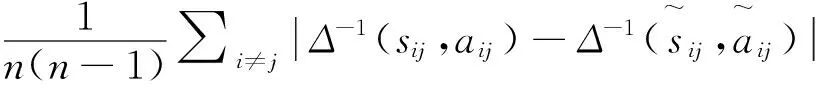

定义2.2.2设定一个阈值δ0,如果语义信息的一致性程度CI<δ0,则可得二元语义信息是具有可接受的乘性一致性的语义偏好关系;反之,则需要调整语义偏好关系,使得调整后的语义偏好关系满足可接受的乘性一致性的要求。
因此,为了尽可能的保留原始决策信息,提出如下的一致性调节的方法:
算法1
输入 二元语义偏好关系(2-TLPR)以及设定的一致性的阈值δ0、参数θ。
输出 一个满足阈值的二元语义偏好关系
步骤1原始二元语义偏好关系,同时,对其迭代次数进行初始化。令At=(Δ-1(sij,aij)t)n×n=A=(Δ-1(sij,aij))n×n且t=0。

步骤3运用定义2.2.1的一致性指数计算语义偏好信息的一致性程度。如果满足设定的阈值,则执行步骤五;如果不满足,则执行步骤四。
步骤4找出满足非一致性程度最大的元素Δ-1(si*j*,ai*j*)t,即满足

Δ-1(sij,aij)(t+1)=
(6)
令t=t+1,并回到步骤二继续计算。

步骤6结束。
下面对一致性指标进行收敛性的证明:
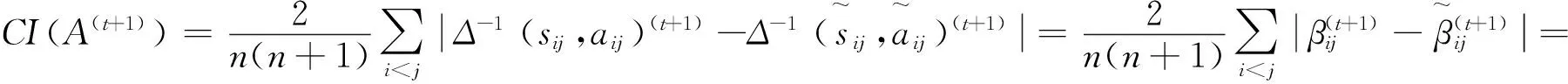
3 二元语义决策模型及其应用
3.1 二元语义决策模型的构建
假设有n个备选方案X={x1,x2,…,xn},专家通过两两比较,给出原始的模糊二元语义,由给出的模糊二元语义做出选择,可以利用如下的模型:
算法2
输入:初始的二元语义偏好关系
输出:各方案最终的排序
阶段A:利用算法1将初始的二元语义进行乘性一致性的改进,得到具有可接受的一致性的模糊二元语义。
阶段B:利用二元语义算术平均算子进行集结,得到每个方案的综合评价:

(7)
阶段C:根据每个方案的综合评价进行排序,选择最终的最佳方案。
3.2 案例分析
及时、有效的应对公共卫生突发事件是保障人民生命安全、维持社会稳定的关键因素。因此,如何做出效益最大化的决策是公共卫生决策的一个重要研究的课题。某社区为应对新冠肺炎,根据本社区的具体情况做出四个方案。为选出最优的应对方案,某社区邀请了专家对四个方案进行两两比较,利用二元语义来表达评价的信息,从而得到专家给定的初始二元语义信息如下所示的A=Δ-1(si,ai)4×4。取可接受一致性指数δ0=0.05,参数θ=0.15。接下来将运用构建的二元语义的模型对方案进行选择,最终选择出满足一致性要求的最优的方案。

(8)
则可得:
(9)
首先,令
A0=(Δ-1(sij,aij)0)4×4=A=(Δ-1(sij,aij))4×4
(10)
利用一致性指数计算式子可以得到A0的一致性指数CI=0.42>0.05;
然后,根据公式6对A0进行迭代,得到最终满足乘性一致性要求的:
(11)
其一致性指数为CI=0.049<0.05。
最后,通过公式7对满足乘性要求的语言信息进行集结得到:
(12)
因此可以得到:x1≻x2≻x3≻x4,故专家们最终采取方案1来应对公共卫生突发事件。
接下来,将利用文献[10]和文献[11]中的方法进行模型的计算,来验证该模型的可行性与有效性。利用文献[10]得到的最终方案的排序为x1≻x2≻x3≻x4,与最终结果是一致的,说明所采用的方法是具有一定合理性的。然而,在文献[11]中得到的最终结果为x1≻x4≻x2≻x3,与所得到的结果具有一定的差异,主要是因为他在计算的时候,首先运用语义平均算子对专家们的初始评价信息进行集结,所采用的方法是首先考虑专家评价信息的一致性,然后在对专家评价信息进行一致性调整以后,对其中满足可接受的乘性一致性语义信息进行集结,提高了专家评价语义的准确性与可靠性。
在与文献[10]进行比较时,都考虑了乘性一致性的改进,但是改进方法略有差异。文献[10]采用乘性一致性的一般式子的变换来构造满足可接受的乘性一致性矩阵;同时采用对数差来度量乘性一致性程度。而采用最简单的二元语义和的比值来构造全新的乘性一致性的矩阵,并运用二元语义信息的差来计算乘性一致性程度。故与文献[10]相比,构造的模型计算更为简便,减少了运算量,同时运行效率较高;并进行迭代,能够更大限度地保留原始决策信息,使最终的结果更具有科学性。
4 结 语
为了使二元语义的决策信息能够最大限度地减少误差,构建了一个基于乘性一致性的二元语义的决策模型。首先,构造了全新的乘性一致性的改进模型,并给出了所涉及参数的限定值;基于乘性指数的迭代算法,不断改进初始的二元语义信息的一致性。其次,通过二元语义的T-OWA算子对得到的满足可接受的乘性一致性的二元语义信息进行集结,并依据集结的结果对方案进行排序,进而选择最佳方案。最后,在公共卫生突发事件的决策问题的事例中,充分证实了提出的决策模型的可行性与有效性,丰富了二元语义决策的研究。
所采用的模型只从方案的单个属性出发,而考虑方案的多属性能使决策考虑的更全面,使决策更具有科学性,因而,可以把该模型应用到多属性决策中作为未来研究的方向。同时,文中的二元语义决策模型采用了二元语义基础的T-OWA集结算子,未来可以采用其他集结算子,以获得更为准确的二元语义信息。

