TA2 钛合金开口柱壳外爆碎片分布研究1)

吴文苍 董新龙 庞 振 周风华

*(宁波大学冲击与安全工程教育部重点实验室,浙江宁波 315211)

†(宁波大学机械工程与力学学院,浙江宁波 315211)

引言

金属材料在爆炸、冲击等高速变形中发生的碎裂现象,一直是冲击动力学与材料领域的研究热点[1-26].最早在二战时期,Gurney[1],Taylor[2],Mott[3-4]等针对炮弹、手榴弹等壳体装药武器在爆炸载荷下的碎裂问题开展分析研究.其中,Mott[3-4]在研究炸弹壳体的动态碎裂时,将二维柱壳碎裂简化为金属环的拉伸断裂问题,并假设断裂的发生具有随机性与瞬时性,提出断裂卸载稀疏波控制碎片特征尺寸的一维统计分析方法,Mott 卸载波思想为后来众多研究奠定了学术基础.随后,一些学者从不同理论出发对金属、岩石、玻璃等材料的碎裂现象进行解释,各自提出了碎片尺寸分布的计算公式,并且做了大量实验加以验证[5-7].尤其,Kipp 等[8-9]在Mott 卸载波的传播距离控制碎片尺度的思想基础上,引入内聚断裂模型,给出了Mott 模型中的特征时间,通过Mott 波传播距离来描述碎裂过程中产生碎片的平均尺寸,其公式形式简单,不需要做关于碎裂过程的随机假设,便于应用.陈磊等[10-11]的一维数值模拟工作表明:Kipp和Grady[8-9]的韧性碎片尺寸公式(G-K 公式)能较好地预测碎片平均尺寸的下限,其中碎片个数和应变率2/3 次幂关系的趋势与Grady[12]、Altynova 等[13],Zhang 等[14]学者的大量一维韧性碎裂实验结果基本一致.Mott 卸载波传播距离控制碎片尺度的思想在一维应力理论框架上很好地描述了固体在冲击拉伸作用下的碎裂过程.

事实上,从军事应用需求角度来说,二维碎裂问题比一维应力膨胀环碎裂问题更具有工程意义.但目前除数值模拟外,简单的包含裂纹传播过程的二维碎裂理论模型尚未出现.对于在二维尺度上均匀膨胀的固体,Grady[12]曾定性地将二维碎裂问题简单地分解为两个一维情况的正交,将二维应力状态下的卸载波简单处理为两个方向上相互独立的一维Mott 波,得到了二维均匀拉伸载荷下的平板碎片的面积尺度,但碎片尺度公式显著高估了双轴拉伸碎片面积.在实验分析方面,Grady 和Hightower[15]通过爆炸驱动4410 钢厚壁圆筒实验,发现对于柱壳爆炸膨胀碎裂,不是单纯的拉伸破坏,而出现了拉伸+剪切的断裂模式.Grady 等[16]建议可将断裂能定义为拉伸与剪切两部分的贡献,并假设金属柱壳的碎片尺度与一维拉伸尺寸相同,但未给出两者的比例及进一步的分析.Hoggart 和Recht[17]实验观察到低爆轰压力下,拉伸断裂为主要破坏模式;而在高爆轰压力下,碎片中更多的是剪切失效,他们认为爆轰压力控制了断裂模式的转变,剪切断裂占断口比例与爆炸压力有关.显然,对于柱壳的碎裂过程及碎片分布,其影响因素要比一维应力复杂,而且还需要考虑断裂模式的影响.

本文对爆炸作用下TA2 钛合金开口柱壳破坏模式及碎裂分布开展研究,探究不同爆炸压力(应变率)下,韧性金属的碎裂特征及其对碎片分布的影响,比较G-K 理论预测公式对于柱壳剪切断裂模式的适用性,探讨剪切断裂能的意义,以期为相关工程分析提供参考.

1 实验设计及碎片回收

1.1 试样材料及实验方法

实验柱壳采用工业纯钛TA2,其密度为4.51 g/cm3,成分组成比为Ti 占99.6%,C 占0.021%,Fe 占0.06%,N 占0.025%,H 占0.004%,O 占0.11%;退火处理后原始组织为α 等轴晶.设计加工成内径19 mm、壁厚3 mm、长度60 mm 的开口柱壳试样.

柱壳外爆实验原理如图1(a),柱壳试样内填充不同的炸药,一端设置传爆药及雷管,如图1(b) 所示.实验中,通过对柱壳内部填充不同密度、不同混合比炸药的方式,来改变实验爆炸压力,获得不同压力特征的载荷.

图1 柱壳外爆实验原理及设计Fig.1 Experimental assembly and site of cylindrical shell

爆炸实验在一个直径为800 mm 的容器中完成,实验中,将柱壳密封并置于充水的塑料袋中,对碎片进行软回收,减小碎片的二次损伤,如图1(c)所示.

1.2 炸药种类及爆轰特性

实验中,在柱壳内部实心填充不同密度、不同混合比炸药,以获得不同的爆炸压力.炸药分别为:密度为0.86 g/cm3的黑索金粉、密度为1.48 g/cm3的黑索金+添加剂的药柱以及密度为1.65 g/cm3的B 炸药药柱.采用探针法分别测试了三种炸药的爆速D,虽然炸药爆炸过程相当复杂[27],但此处可以忽略不同炸药的化学性质及爆炸产物的影响,采用简化公式[28]对炸药的爆炸C-J 压力PC-J进行估算,如表1所示.

表1 不同装药条件下的爆速及爆压Table 1 Detonation velocity and detonation pressure under different charge conditions

2 实验结果及分析

2.1 碎片特征

2.1.1 宏观断裂特征

图2 所示为不同爆压实验下回收得到的典型碎片,主要碎片呈长条状,长度与原始柱壳长度几乎相同,少量在轴向上发生断裂.随爆炸压力增大,回收到的碎片数量增加,宽度更趋于均匀.

图2 不同爆压下的回收碎片Fig.2 Recovered fragments under different detonation pressures

图2 不同爆压下的回收碎片(续)Fig.2 Recovered fragments under different detonation pressures(continued)

对实验回收的碎片宏观观察显示:柱壳均为剪切断裂破坏,碎片横截面存在五种典型的特征,如图3 所示,未见拉伸及拉剪混合断裂模式.绝大部分碎片呈图3 所示的a,b,c,d 及e 五种特征,其中,d,e 碎片都是轴向长度较短的碎片,基本是a,b,c 三种主要条状碎片交界处剥落产生的小碎片.值得注意的是:实验中对每块碎片逐一观测,没有发现碎片中有与a 形状相反的内壁短、外壁长的倒梯形状碎片,这可能与柱壳断裂起始及Mott 卸载波传播相关.

图3 典型碎片截面示意图Fig.3 Typical cross-section of fragments

进一步观察发现:(1)在较低爆压(7 GPa)下,回收碎片主要呈长条状,长度基本与原始柱壳的长度相同,碎片的断口方向与径向近似成45°或135°,碎片截面主要呈a,b,c 三种类型;个别宽度较大的碎片内、外表面存在较多未断开的轴向裂纹,这是由于裂纹沿轴向并未发展完全,最终没有形成独立存在的新碎片,如图4(a)所示.(2)当爆压为22 GPa 时,除长条状碎片,沿轴向断裂的小碎片数量增多.另外,碎片内表面存在沿环向分布台阶及沿轴向的微裂纹,如图4(b)所示.(3)当爆压为25 GPa 时,碎片尺寸较为均匀,整体形状更加规则,断口平滑光亮,呈发蓝、发紫颜色,但外表面存在一些沿轴向发展的变形集中带或微裂纹如图4(c)所示.特别值得注意的是,碎片截面的剪切断口方向均为同一旋向,即图3 中碎片b 形式.胡海波等[29]曾在多种金属爆炸碎片中观察到类似的单旋破坏现象,但到目前为止其机制并不清楚.

图4 不同爆压下的典型碎片Fig.4 Typical fragments under different detonation pressures

2.1.2 微观断裂机制

对三种爆压下典型碎片横截面进行微观金相分析,如图5 所示.微观金相显示:在较低爆压(7 GPa)下,碎片截面较为平整,虽然在内、外表面局部存在裂纹,前端可见绝热剪切局域化带特征,但碎裂断口不是由绝热剪切带破坏导致的,如图5(a) 所示.在22 GPa 爆压下,断口为与径向成45°的剪切断裂,但与7 GPa 爆炸压力作用下不同,在试样内表面分布着一组沿剪切方向(与径向45°与135°)交叉、平行的多重绝热剪切带,多重剪切带间相对滑移,一些裂纹已沿剪切带扩展,在碎片内表面形成裂纹或台阶,与宏观碎片内表面所见的沟槽及微裂纹相对应.断口是裂纹沿剪切带扩展至外表面形成的绝热剪切断裂模式,如图5(b).在25 GPa 爆压下,典型碎片截面成近似平行四边形,内表面存在一组与径向成45°、平行的多重绝热带及沿剪切带发展的裂纹,但趋于单旋的绝热剪切断裂模式,如图5(c)所示.

对不同爆炸压力下的柱壳碎片截面的宏观及微观分析可见:虽然TA2 钛合金柱壳宏观断口均呈现剪切型断裂,但微观机制不同.在较高爆压(22,25 GPa)下,为绝热剪切断裂机制控制;而在较低压力(7 GPa)下,为非绝热剪切断裂.另外,对于绝热剪切带控制的断裂,试样内表面呈现的台阶分布与多重绝热剪切带滑移位置相对应,剪切带之间的相对错动,在碎片内表面形成沿轴向分布的沟槽及微裂纹.

2.2 碎片统计方法及分布规律

2.2.1 统计方法

回收碎片特征显示:不同爆炸压力下的碎片主要呈长条状,与试样长度相近.小碎片主要是由于局部剥落,或不同截面剪切裂纹发展交错造成断裂.因此,柱壳爆炸膨胀断裂过程可近似假设为定常爆轰作用下的平面应变问题,采用统计碎片宽度方法来表征碎片的特征尺寸.由于剪切裂纹沿轴向呈台阶分布,不同截面尺寸存在较大差别,直接多点测量碎片平均宽度误差较大.另外,截面存在图3 所示的多种形状,难以统一定义宽度.沿碎片轴向多点厚度测量发现:同一试验回收的碎片沿轴向厚度较为均匀,为此,采用称重及测量碎片平均厚度、长度来统计碎片.进一步假设材料变形体积不变,计算碎片的名义宽度w

式中,wi为碎片宽度,mi为碎片质量,ρ 为材料密度,li为碎片长度,hi为平均厚度,下标i代表第i块碎片.

2.2.2 碎片质量分布规律

统计时,采用天平对每块碎片进行称重,并同时测量碎片的长度及上中下3 个位置厚度.表2 为不同压力下典型试样碎片平均厚度及碎片的回收率η.可见随爆炸压力增大,碎片厚度减小.

表2 不同爆炸压力下回收碎片统计Table 2 Statistics of the recovery fragments

图6 给出了不同爆炸压力下回收碎片数量分布,可以看到:在较低爆压下的碎片质量分布区间范围更大.

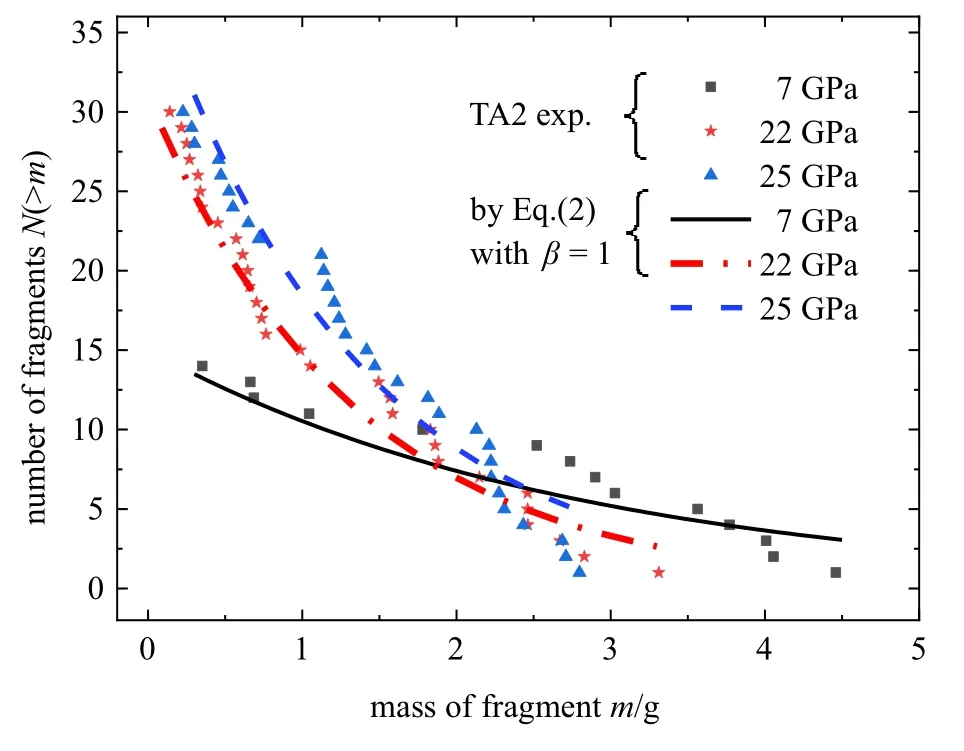
图6 碎片质量分布Fig.6 Mass distribution of fragmentation

由于柱壳断裂起始位置存在随机性,Mott 和Linfoot[30]在对炸弹碎片特性分析中,采用统计方法建立统一尺度比拟模型,以便评估参数变化对弹头碎片特性影响,并提出了碎片质量的泊松统计分布关系.Grady 和Kipp[31]考虑到炸药、装药特征和外壳金属广泛性,提出采用具有更广适应性的形式

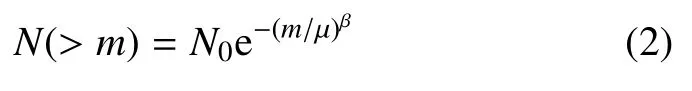
其中,N(＞m) 为质量大于m的碎片数,N0为碎片总数,m为碎片质量,μ 为碎片质量参数,β 为分布形状参数.这一关系事实上包含了Mott 模型的特例,β=1/2 即对应于Mott 和Linfoot[30]提出的泊松统计分布形式.图6 中同时给出了按式(2)中β=1 时拟合的曲线,可见取β=1 与实验碎片质量分布趋势符合较好,但对于大碎片的分布描述并不够准确.这主要有两个原因:一方面是由于较多的小质量碎片未完全被回收;另一方面,与一维应力拉伸断裂不同,二维柱壳断裂发展不充分,如图4 和图5 所示,大尺寸碎片表面存在系列轴向裂纹,如果充分碎裂,碎片宽度应更小.

在碎片质量分布实验研究方面,Mock 和Holt[32]曾对工业用纯铁和两种不同热处理的厚壁HF-1 钢管(径厚比为3～4) 爆炸碎裂碎片分布进行了统计,指出β=1/2 的指数模型可以很好描述碎片质量分布规律.另外,在一维应力碎裂中,很多学者也都采用β=1/2 的分布.而Grady 与Kipp[31]针对金属球壳动态破碎研究中,认为采用β=1 的模型能更好描述了碎片的分布,并且明确认为μ 为特征尺寸碎片的质量.Odintsov[33]对Mott 形式的碎片质量分布规律做过更详细的研究,也认识到不同大小碎片段分布的断裂机制可能不同,规律也可能不同.

事实上,碎片质量分布的规律性与Mott 卸载波控制相关.分析认为,对于一定的装药系统及爆炸碎裂过程,存在随机的不充分碎裂,导致实际碎片尺寸在统计上的不均匀性,使分布变宽.按式(2)统计拟合时,β 值趋于变大.如在相同柱壳壁厚下,内径越大,爆炸碎裂越充分,碎片越小并趋于均匀,β 的值应会变得较小.与柱壳碎片相比,一维应力动态膨胀环碎片分布更接近β=1/2.

虽然断裂存在随机性,但在给定的加载率下,碎片分布的规律性与Mott 卸载波相关,二维碎片分布应具有特征尺寸,下面进一步就柱壳碎裂碎片尺寸分布特性进行分析.

2.2.3 碎片宽度分布及特征尺寸

采用碎片的环向宽度来表征碎片的尺寸,图7 给出按式(1)计算的TA2 柱壳不同爆压下的碎片宽度分布,可见尺寸分布存在相似性,大多碎片尺寸集中带靠近较小尺寸区域,爆炸压力越低碎片尺寸分布宽度越大.采用Weibull 积累分布函数拟合

其中,N(＞s) 表示碎片尺寸大于s的碎片个数,N0为碎片总个数,smin为有效最小碎片尺寸,n为形状参数,s0为标度参数,s＞smin.周风华等[34]、郑宇轩等[35]对一维应力韧性金属圆环碎片长度尺寸研究认为:n=2 时的Weibull 函数,即Rayleigh 分布可以较好描述碎片宽度尺寸分布.对于平面应变柱壳碎片宽度分布拟合比较发现,Rayleigh 同样可以较好地来表征柱壳碎片的尺寸分布,如图7 所示,即满足

其中s＞smin,从图7 可见:虽然碎片数量较少,但不同爆炸压力下平面应变柱壳碎片宽度分布仍与Rayleigh 分布趋势吻合较好,并且随爆炸压力增大,碎片数量增加,分布曲线趋势符合更好.

图7 碎片宽度分布及概率拟合Fig.7 Fragment width distribution and probability fitting

不同爆压下碎片分布规律结果显示:(a)Rayleigh分布形式可以描述柱壳碎片尺寸分布规律,并随着加载率的提高,Rayleigh 概率密度分布趋向变窄;(b)随着爆压(加载率) 的增大,碎片特征尺寸呈减小的趋势.另外,爆压为25 GPa 时的回收得到的碎片数量虽然增加,但最小碎片尺寸、特征尺寸都较爆压为22 GPa 的略大.这与爆压为25 GPa 时裂纹大多为沿单旋绝热剪切带发展相关,由于断裂面单旋发展,这样交叉的裂纹少,使得剥落的小碎片数量减小.

按Rayleigh 分布可计算得到不同爆炸压力下的碎片特征尺寸

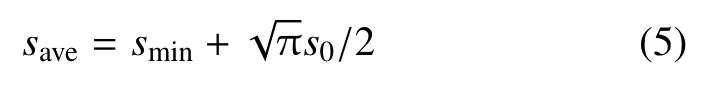
计算得到的爆压7 GPa,22 GPa,25 GPa 下碎片的特征尺寸分别为5.67 mm,3.87 mm,4.59 mm.可见:爆炸压力(应变率) 增大,碎片特征尺寸随应变率增大出现先减小,随后又增大的现象.按Mott 卸载波传播距离控制碎片特征尺寸思想,理论上,应该随应变率提高,碎片尺寸减小.但爆炸压力25 GPa 时碎片特征宽度反而比22 GPa 增大.这与25 GPa 时断裂扩展模式改变有关,在25 GPa 时,断裂裂纹呈单旋方向,碎片截面为平行四边形,使裂纹交叉产生的剥落小碎片少,实际碎片分布跨度相对要小.事实上,从控制TA2 钛合金在较高爆压下碎裂绝热剪切断裂机制看,较高爆压25 GPa 时的多重绝热剪切带间距还是比22 GPa 时减小(如图4 和图5 剪切带间距).

2.2.4 尺寸归一化

对不同爆压下碎片的特征尺寸对每块碎片宽度分布归一化处理,即

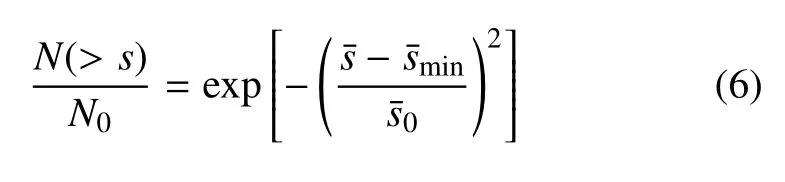
图8 不同爆压下归一化尺寸累积分布Fig.8 Cumulative distribution of normalized sizes under different detonation pressures

近似地,对图8 不同爆压下碎片归一化尺寸“台阶状”数据分布集中带取平均值计算其相邻台阶间距并取最小值i=1,2,···,n},计算得到7 GPa,22 GPa 和25 GPa 下“台阶状”碎片尺寸最小间距分别为1.71 mm,0.33 mm 和0.42 mm.对于碎片的自组织“特征尺寸”,Mott 提出是由拉伸断裂过程产生的卸载波(Mott 波)传播距离控制,Grady-Kipp基于材料拉伸断裂软化演化特征时间的一维应力韧性碎裂模型抓住了韧性碎裂过程中的主要矛盾,周风华等[10-11]的数值模拟工作表明Grady-Kipp 模型所预测的韧性碎片特征尺寸公式较好地预测碎片的平均尺寸的下限,与Grady[12],Altynova 等[13],Zhang等[14]学者的一维韧性碎裂实验结果也一致,下文对剪切特征尺寸预测及影响因素进行讨论.

3 关于二维碎裂特征尺寸

3.1 剪切碎裂G-K 公式

对于柱壳拉伸碎裂破坏,Mott[4]提出了卸载波控制碎片特征尺寸的分析思想,给出了一维应力膨胀环碎片的特征尺寸分析方法.Grady 等[36]、Kipp等[8]进一步扩展了Mott 思想,采用内聚断裂模型描述断裂能量耗散和应力释放率,给出了Mott 模型中的特征时间,无需引入碎裂起始随机假设,直接得到了Mott 波传播距离,确定碎片的特征尺寸

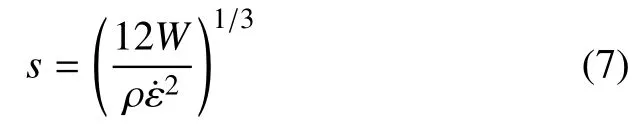
Grady 等[16,37]进一步又对拉伸碎裂模型进行修改,来解决二维剪切局域化自组织问题,认为在绝热剪切情况下,式(7)仍适用,只要将W变为绝热剪切带断裂时单位面积耗散的塑性功,则绝热剪切带的自组织间距为

进一步,如假定剪切断裂时的应力释放由热软化引起,假设有以下形式

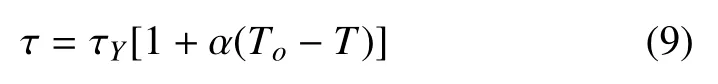
式中,τY为流动应力,α 为热软化系数,T-T0为绝热温升.简单取α=1/ΔT,即线性热软化,考虑剪切带内绝热温升,得到剪切带形成的最小局域化时间,导出多重剪切带间距s0为

其中,c为材料比热,χ 为热扩散系数.由式(8)、式(10)得到了在绝热剪切局域化过程中的能量耗散

对于金属圆筒的碎片的特征尺寸,Grady 认为同样可由界面断裂能W表征,形式与一维应力碎裂情况下推导所得式(7)相同.只是当断裂面的形成由拉伸断裂和剪切断裂两种失效模式共同主导时,断裂能需要考虑拉伸和剪切两种破坏在断裂面中所占比例,以适当的方法加权计算.拉伸失效断裂能可采用金属断裂韧性Kc估算

而剪切失效断裂能可采用式(11)的能量耗散计算.

3.2 特征尺寸及断裂能

3.2.1 碎片特征尺寸

实验显示:TA2 钛合金柱壳外爆碎裂均为剪切断裂,未见拉伸及拉伸+剪切混合断裂模式.因此,采用材料剪切失效断裂能W,按G-K 剪切式(8)分析碎片特征尺寸.设柱壳爆炸膨胀变形过程近似为平面应变状态,其应变近似取为

式中,R(t)为t时刻的柱壳半径,R0为初始柱壳半径.开口柱壳断裂近似作为平面应变膨胀破坏,则剪切应变γ 为

其中,V0为柱壳断裂时刻碎片速度.

Gurney[1]基于炸药能量平衡,提出了一个估算壳体破片最终速度公式.Lloyd[38]考虑柱壳为有限长度的影响,两端稀疏作用降低了壳体内炸药爆轰产物膨胀做功能力,会使壳体破片最终速度V0降低,对Gurney 速度公式进行修正

式中,M/C是柱壳与炸药质量之比,E为格尼能通过炸药密度及爆速估算[39-40],R0/L是柱壳的内径与长度比.Goto 等[41]和Lambert 等[42]应用该公式预测柱壳断裂时速度与测试结果均符合较好.

假设柱壳膨胀断裂后,碎片的厚度不再变化,则可采用回收碎片的平均厚度来估算柱壳断裂半径

式中,L0为柱壳高度,h为壁厚,li,wi,hi为同一碎片的长度、宽度、厚度,η 为碎片质量回收率.

采用上述方法对柱壳断裂时速度及半径估算虽然与实际存在偏差,但在同一条件下的实验中应具有一定的可比性.表3 分别给出了不同炸药作用下按式(16)、式(17)、式(15)计算柱壳的膨胀速度V0、断裂半径R*及其应变率的结果,则按式(14)计算的断裂应变分别为0.37,0.43,0.45,即随着爆炸压力的提高、应变率增大,断裂应变增大.

表3 不同炸药作用下柱壳断裂参数估算Table 3 Estimation of parameters of cylindrical shell under different explosives

对TA2 纯钛的动态剪切性能及变形过程的绝热温升进行分析,近似取流动应力τY为其屈服强度Y=500 MPa,材料比热c=500 J/(kg·K),材料热软化系数α=1/ΔT=2.5×10-3K-1[43].不考虑压力对热传导系数的影响,则χ=κ/(ρc),TA2 钛等压热传导系数κ=17 W/(m·K).图9 给出了实验回收碎片统计分布分析得到的碎片特征尺寸及采用G-K 剪切式(8)预测的碎片特征尺寸随应变率变化的比较,其中,剪切断裂能按式(11)计算.可见:G-K 式(8)预测的碎片特征尺寸与实际碎片相差很大.G-K 公式预测的碎片特征尺寸(0.95 mm,0.75 mm 和0.72 mm)远小于回收碎片特征尺寸(5.67 mm,3.87 mm 和4.59 mm),而更接近上节7 GPa,22 GPa 和25 GPa 下归一化分析时近似得到的“量子化特征间距”1.710 mm,0.332 mm 和0.417 mm.

图9 碎片尺寸随应变率Fig.9 Variation of fragment size with strain rate

实际上,G-K 式(8)建议采用的剪切断裂能是基于绝热剪切带形成分析得到的最小能量释放率,而实验回收碎片微观分析显示,不同爆压下柱壳的碎片断裂模式并不相同,在7 GPa 压力下碎片断口虽为剪切断裂,但并不是绝热剪切带破坏.图9 中同时还给出22 GPa 和25 GPa 爆压下典型碎片微观分析测量得到的多重绝热剪切带的平均间距,可见:G-K 剪切式预测的碎片特征尺寸与多重绝热剪切带间距随应变率变化更为接近.

对于实验碎片特征尺寸与G-K 预测值的差别,主要包括以下几个方面原因:(1) G-K 剪切断裂公式(8)建议的剪切断裂能是绝热剪切破坏的耗能,即使对高爆压下柱壳绝热剪切碎裂,其断裂并也不充分,碎片中还包含多条平行、交叉绝热剪切带,实际中并不是每条剪切带最终都形成裂纹或断口,高压下量子化的“特征尺寸”反映的是多重绝热剪切带的间距,碎片尺寸应为多重绝热剪切带特征间距的倍数;(2)许多裂纹沿柱壳轴向没有得到充分发展断开,尤其对于二维问题,不同截面断裂起始的随机性,导致实际和预测模型差别较膨胀环碎裂相差更大;(3)对于低爆压,由于不是绝热剪切断裂破坏,采用绝热剪切断裂能分析预测,造成两者的差别.

可见:Grady-Kipp 剪切式(8)、式(11) 是对多重剪切带间距的分析,其结果与实际碎片尺寸相差两个数量级,Grady-Kipp 给出的剪切断裂公式与实验多重绝热剪切带间距符合较好.

3.2.2 绝热剪切断裂能

Grady-Kipp 的碎片特征尺寸分析公式依赖于断裂能释放率,因此,实际分析中明确断裂模式及其断裂能极为关键.对于绝热剪切演化,周刚毅等[44]曾采用平板帽型剪切试样对相同TA2 钛的绝热剪切破坏演化特性开展实验研究,测试了从剪切变形到绝热剪切破坏过程的等效应力-应变全曲线及相应剪切区的绝热温升,如图10 所示,阴影面积W实际上即为应变率为3100 s-1时的绝热剪切破坏的耗能,近似为6 kN/m.

图10 TA2 绝热剪切破坏演化的热-力学响应[44]Fig.10 Thermal-mechanical response of A TA2 adiabatic shear failure[44]

同时,可以利用实验回收碎片的特征尺寸按GK 式(8)反演剪切断裂能,按回收碎片中多重绝热剪切带平均间距按式(11) 反演绝热剪切破坏断裂能.图11 分别给出了按柱壳碎片尺寸、多重绝热剪切带平均间距反演的断裂能与实验测试得到的绝热剪切带破坏过程的断裂能的比较.可见:绝热剪切断裂能明显低于剪切断裂能,而G-K 公式导出的绝热剪切带形成的最小耗能比帽型剪切实验得到的断裂能略小,两者比较相近.低爆压下的剪切断裂时,材料剪切断裂能可能远大于绝热剪切断裂能.

图11 TA2 剪切断裂能分析Fig.11 Estimation and comparison of TA2 shear fracture energy

可见:二维柱壳碎片的自相似特征尺寸不仅依赖于材料的应变率、断裂模式(断裂能不同),另外还与柱壳断裂的充分程度相关.

4 结论

对TA2 钛合金开口柱壳在不同装药条件下的碎裂特性开展实验研究,通过对回收碎片的统计及典型碎片的宏微观分析,探讨碎裂断裂模式及碎裂特性,结果显示:

(1)TA2 钛合金柱壳在实验爆压下宏观断口均为剪切断裂模式,但不同压力下,断裂机制不同.在较低压力下(7 GPa),为非绝热剪切带破坏,而随压力增大至22 GPa,25 GPa 柱壳发生多重绝热剪切断裂,并且在25 GPa 时,趋于单旋绝热剪切破坏现象.

(2)随爆压增大(加载率)增大,柱壳碎片质量、尺寸减小,但25 GPa 时的碎片特征宽度反而较22 GPa时略有增大,这是由于25 GPa 时,多重绝热剪切带及裂纹趋于单旋发展,碎裂时裂纹交叉少,崩落产生的小碎片数量较少造成的,而25 GPa 时碎片内表面处多重绝热剪切带间距,较22 GPa 还是减小的.

(3)柱壳爆炸膨胀碎裂的碎片质量分布符合β=1 的指数分布,分析认为对于一定的装药系统及爆炸碎裂过程,由于存在随机的不充分碎裂,使分布变宽,β 值趋于变大.如在相同柱壳壁厚下,内径越大,爆炸碎裂越充分,碎片越小并趋于均匀,β 值应会变得较小,更趋于Mott 和Linfoot[30]提出的泊松统计分布形式.

(4) Weibull 分布中的Rayleigh 形式可以较好描述柱壳碎片的宽度分布规律,并且随着加载率的提高,Rayleigh 概率密度分布逐渐变窄.不同应变率下的碎片尺寸累积分布归一化结果显示,碎片分布具有相似性,呈现“量子化”特性,即碎片尺寸为特征尺寸的倍数.

(5)TA2 柱壳碎片特征尺寸远大于G-K 剪切断裂公式预测的特征尺寸,G-K 剪切式与高爆炸压力下的多重绝热剪切带间距相近;G-K 剪切断裂公式采用的是绝热剪切带形成的最小耗能分析,不适用于低压下的非绝热剪切断裂情况.