中职数学教学中的逻辑推理培养——以《平面的基本性质》为例

邗江中等专业学校 王小敏

教育部《关于全面深化课程改革 落实立德树人根本任务的意见》中明确提出“核心素养”概念，将“核心素养”作为各学科课程目标。

《中等职业学校数学课程标准（2020）》中明确规定了数学六大核心素养：数学运算、直观想象、逻辑推理、数学抽象、数据分析、数学建模。同时提出使学生初步学会“用数学眼光观察现实，用数学思维分析现实，用数学语言表达现实”。

逻辑推理是数学思维的关键素养，培养学生从事实和命题出发，发现现实背后的规律，以规律为原则，从数学角度发现和提出问题，用数学知识和方法分析和解决问题。针对如何将逻辑推理核心素养融入中职数学课堂教学中，本文以“平面的基本性质”为例，从公理及推论的得出的角度进行阐述。

一、逻辑推理的基本内涵和学业质量水平

（一）逻辑推理的基本内涵

逻辑推理有三种方式：演绎、归纳和溯因。给定前提、结论和规则，而前提导致结论，例如：

前提：下雨了。

规则：下雨使草地变湿。

结论：草地是湿的。

演绎：用来决定结论。

归纳：用来决定规则。

溯因：用来决定前提。

（二）逻辑推理的学业质量水平

1.水平一

在熟悉的单一情境中，能辨识三种推理，能辨明数学命题中条件与结论的逻辑关系，会有条理地表述简单的数学命题，能够明确数学问题中的前提、结论和规则的关系，能够进行简单的逻辑推理，从而运用逻辑推理发现问题和解决问题。

2.水平二

在熟悉的关联情境中，在水平一的基础上略微提高，并善于运用逻辑推理分析问题、说明问题和论证问题。

二、以平面的基本性质为例

逻辑推理在中职数学教学中有多个章节涉及，本文仅以《平面的基本性质》为例进行阐述。

（一）平面的基本性质的三个公理

生活情境：一扇门可以自由转动，如果锁住了，门就固定住了，为什么？

教师启发引导：门转动是什么原理？

学生回答：铰链。

教师：如果锁住了，门就固定住了，为什么？

学生回答：一边用铰链，另一边有门锁。

教师：什么原理呢？学完本节内容，我们可以解决这个问题。

1.公理1

学生动手实践：将三角板的两个顶点放在桌面上。

教师启发引导：会发现这条边就在桌面上，为什么？

学生思考：因为三角板的两个顶点在桌面上，所以归纳出这条边上所有的点都在桌面上。

教师启发引导：两个顶点代表两个点，这条边所在直线与平面的关系呢？

学生可以归纳出：如果两点在一个平面内，那么两点所在的直线在这个平面内。

教师再启发：我们通过逻辑推理得出了结论，如何将语言表述得更严谨？

学生在教师的启发下小组交流合作，得出严谨的公理1。

练一练：画出公理1 的图形，再使用数学符号语言表示。

2.公理2

学生动手实践：三角板的一个顶点落在平整的桌面上。

教师启发引导：三角板与桌面有几个交点？

学生回答：一个交点。

教师再启发引导：三角板所在的平面与桌面有几个交点？

学生回答：有无数个交点。

教师再启发引导：这无数个交点有什么共同特征？

学生回答：可以连成一条线。

教师再启发引导：这条线与最初的交点有什么关系？

学生回答：这条线过交点。

教师再启发引导：将语言表述得更严谨些。

学生在教师的启发下小组交流合作，得出严谨的公理2。

练一练：画出公理2 的图形，再使用数学符号语言表示。

3.公理3

学生动手实践：三角板的三个顶点都落在平整的桌面上。

教师启发引导：三角板就紧贴在桌面上，为什么？学生思考回答：因为三角板的三个点都在桌面上。教师再启发引导：这三个点位置有什么关系？

学生回答：不在同一直线上。

教师再启发引导：如何将语言表述严谨？

学生思考，小组交流，得出由不共线三点的条件，可以确定一个平面的公理3。

练一练：画出公理3 的图形，再使用数学符号语言表示。

（二）平面的基本性质的三个推论

1.推论1

教师启发提问：由不在同一直线上的三点可以确定一个平面。是否还有其他确定平面的条件？动手画一画、连一连。

学生动手画图：过点A，B，C中的其中两点A和B作了一条直线。

教师启发引导：确定一个平面，有其他条件吗？

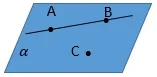
学生通过推理得出：过AB的直线和点C也可以确定一个平面。

教师再启发引导：换成一般的情况，不限于具体直线，也不限于哪个点，有什么结论？

学生思考，小组交流，得出由直线和直线外一点的条件，可以确定一个平面的推论1。

2.推论2

教师启发提问：推论1 是作了一条直线，那么还可以怎么作图呢？

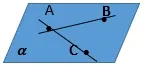
在推论1 的基础上，学生作出了两条相交直线，过AB和AC的直线相交于点A。

教师启发引导：此时我们能得出什么结论？如果不限于具体直线呢？

学生思考，小组交流，得出由两条相交直线的条件，可以确定一个平面的推论2。

3.推论3

教师启发提问：在推论2 的基础上，我们还可以如何作图，得出确定一个平面的条件？

学生动手实践：作出过AB的直线，并过点C作出AB所在直线的平行线。

教师启发引导：此时我们得出确定平面的什么条件？如果不限于具体的直线呢？

学生思考，小组交流，得出由两条平行线的条件，可以确定一个平面的推论3。

三、发现问题，解决问题

中等职业学校数学课程的任务，是培养学生的数学核心素养，使学生在以后的生活和学习中，逐步形成运用数学知识和经验发现问题的意识，逐步提高运用数学的方法和工具解决问题的能力，而逻辑推理是终身学习的最重要的核心素养。

【现实案例】

1.照相机的三脚架为什么能稳定地支撑在桌面上？

2.建筑工人用水泥浇注完地面后，要检查地面是否平整，用什么方法？

3.回到本节开头的生活情境：为什么门锁住了，就固定了？

学生思考回答，分别使用了本节课学习的公理与推论来解决现实生活案例。

【总结】

逻辑推理核心素养目标：使中职学生能够基本掌握逻辑推理的一般方法，能通过逻辑推理把握事物之间的基本联系，基本形成条理清楚的思维能力和表达能力，养成敢于质疑、善于思考、严谨求实的品格。

本节以平面的基本性质的三个公理及推论为例，通过动手实践、启发思考、练一练等流程，引导学生通过逻辑推理的方法，由特殊到一般和类比的方式，得出公理和推论。