守恒型Allen–Cahn 方程的显式高阶保极值格式

孙竟巍 张弘 钱旭 宋松和

(国防科技大学文理学院,长沙 410073)

1 引言

经典Allen–Cahn 方程是相场模型中关于自由能泛函:

的一个典型的梯度流问题.这里,u为一个实值未知函数,Ω 为具有Lipschitz 边界∂Ω 的有界区域.以(·,·)表示Ω 上的L2内积,对应的L2范数记为∥·∥2.

在两相流问题中,u通常表示相变量,ϵ>0 代表两相间的界面宽度,F(u)则表示某种非线性势函数.经典Allen–Cahn 方程可以视为在能量泛函(1.1)下的L2梯度流:

其中f(u)=−F′(u).方程(1.2)是由Samuel M.Allen 和John W.Cahn[1]于1979 年提出,用于描述结晶体中反相边界的运动模型,如今已被广泛用于模拟自然界中的界面运动和相变,如[2,3].Allen–Cahn 方程(1.2)具有能量耗散律:

此外,Allen–Cahn 方程还有一个重要的性质:极值原理(Maximum principle preserving,MPP).极值原理作为研究相场模型物理特性的一个重要的数学工具,在近些年受到越来越多学者的关注.极值原理是指如果方程的初值和边值以某个大于0 的特定常数逐点为界,那么计算所得到的解也始终以该常数为界.作为相场模型的一个重要的物理特征,极值原理对于具有物理意义的数值解而言是必不可少的.不保持极值原理的数值算法可能使得数值解出现病态情况并且数值模拟会发生“爆破”现象.所以人们在对Allen–Cahn 方程所描述的动力学进行数值模拟时,希望保持这个特性.

经典Allen–Cahn 方程虽然满足能量耗散和极值原理,但由于其并不遵循质量守恒定律,可研究的范围具有一定的局限性.为进一步改善Allen–Cahn 模型来扩展相关动力学研究范围,学者进行了广泛且深入的研究.目前主要有两类修正的守恒型Allen–Cahn 方程.一类是由Rubinstein 和Sternberg[4]将非局部具有空间依赖的拉格朗日算子引入到经典Allen–Cahn 方程中,使得修正的方程解具有能量守恒性质;该算子简记为RSLM,形式为:

另一类是由Brassel 和Bretin[5]将局部-非局部且时空依赖的拉格朗日乘子引入到经典Allen–Cahn方程使其解满足质量守恒;该算子简记为BBLM,形式为:

近几年内,学者对Allen–Cahn 型方程极值原理这个特性的关注密切,许多针对该方程构造的保极值格式应运而生.文献[7,8]针对经典Allen–Cahn 方程将有限差分法与稳定化半隐方法相结合构造了一阶和二阶的保极值格式.杜强等[9]针对非局部Allen–Cahn 方程构造了一阶和二阶的指数时间差分格式.侯天亮等[10] 对空间分数阶Allen–Cahn 方程提出了保极值的二阶Crank–Nicolson 有限差分方法.最近,廖洪林等[11]针对时间分数阶Allen–Cahn 方程提出了二阶的时间自适应保极值格式.然而很少有文献研究关于守恒型Allen–Cahn 方程的保极值格式.文献[12]针对守恒型Allen–Cahn 方程构造了无条件保极值格式,但该格式精度最高只能达到二阶.就我们所知,还没有任何文献针对守恒型Allen–Cahn 方程构造的保极值格式精度超过二阶.而高阶精度对于高维和强复杂度问题的研究十分重要,因此我们迫切需要一个高精度的保极值格式来求解守恒型Allen–Cahn 方程.

本文借助时间方向上的积分因子两步Runge–Kutta 方法来构造高精度保极值格式.积分因子Runge–Kutta 方法近些年来已被广泛应用到刚性常微分方程的计算中[13,14],积分因子Runge–Kutta 方法可以看作是传统Runge–Kutta 方法的一个延伸,尤其对于含有强刚性的线性项问题格外有效.其主要思想在于应用指数积分因子来消除线性项的强刚性并且用Runge–Kutta 方法进行时间积分.文献[15,16]使用积分因子Runge–Kutta 方法发展了经典Allen–Cahn 方程的最高四阶精度保极值格式.文献[17]针对经典Allen–Cahn 方程将积分因子Runge–Kutta 方法结合线性稳定化技术构造了最高三阶精度的无条件保极值格式.本文使用的两步Runge–Kutta 方法(Two-step Runge–Kutta method,TSRK)作为传统Runge–Kutta 方法的扩展,有接近30 年的研究历史.两个方法的区别在于两步Runge–Kutta 方法应用前一时间层和当前时间层的信息构造积分器,继而使得两步Runge–Kutta 法可以用较少的级数得到与单步Runge–Kutta 法相同的精度.

本文的其余部分安排如下.第二节介绍关于RSLM 形式的守恒型Allen–Cahn 方程和半离散系统的一些预备知识.第三节构造积分因子两步Runge–Kutta 格式并证明该格式可以保持极值原理和保持质量守恒,随后给出该格式的误差分析.在第四节,通过一系列的数值实验来验证数值格式的有效性和优势所在.在最后给出结论和展望.

2 预备知识

2.1 具有非局部拉格朗日乘子的守恒型Allen–Cahn 方程

在周期边界条件下,将RSLM 形式的拉格朗日乘子[4]引入经典Allen–Cahn 方程(1.2)中,得到RSLM 形式的守恒型Allen–Cahn 方程:

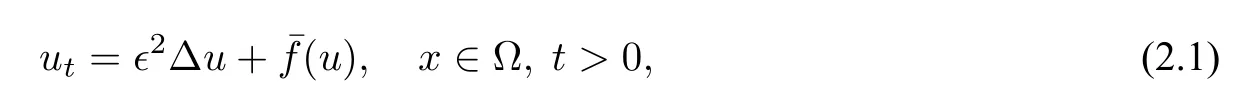
这里,修正的非线性项定义为

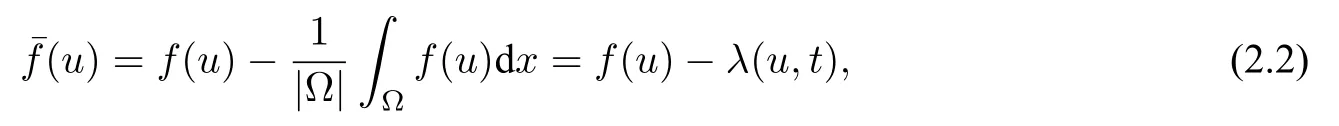
其中λ(u,t)=(|Ω|是Ω 的Lebesgue 测度)是拉格朗日乘子.对于RSLM 形式的守恒型Allen–Cahn 方程(2.1)而言,文献[4,12]推导出(2.1)具有极值原理时对非线性项的要求.

假设1([4,12]) 存在一个常数β >0 使得

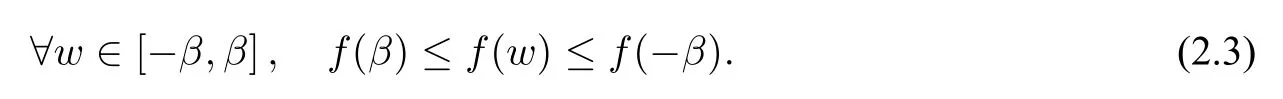
下面给出守恒型Allen–Cahn 方程(2.1)的极值原理.

定理1([4,12]) 给定一个常数T >0,假设u(t)∈C1(0,T;C2(Ω))是带有周期边界条件的守恒型Allen–Cahn 方程(2.1) 的经典解.如果假设1成立并且对于任意x ∈Ω ∪∂Ω,初值满足≤β,那么对于任意t>0,≤β成立.

对于广泛使用的多项式势函数F(u)=,非线性项为

文献[12]证明了对于任意β ≥,(2.4)中的f(u)都满足假设1.而当β=时,我们有|f′(ξ)| ≤3,∀|ξ| ≤β.因此由于非局部RSLM 算子λ(u,t)的引入不能保证解的局部性,从而改变了经典Allen–Cahn 方程原本的极值.然而,在周期边界条件下,这个非局部项抵消了质量的变化,即

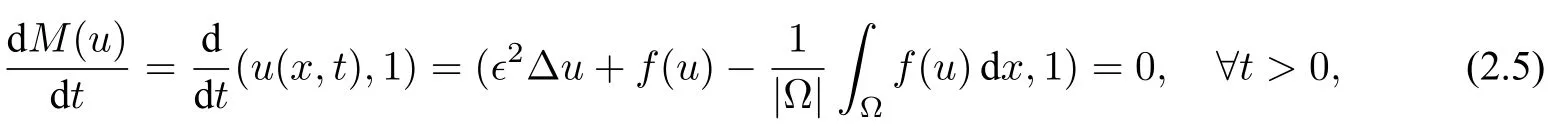
并且没有影响原始的能量耗散律:

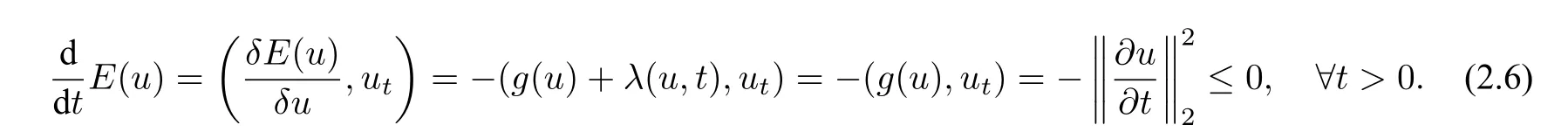
这里,能量泛函是(1.1),g(u)=

2.2 有限差分半离散系统

作为一个常用的空间离散方法[15,16,17],二阶有限差分法将拉普拉斯算子离散为M-矩阵,这样可以继承格式中一些诸如极值原理等的关键性质.下面给出一维空间中二阶有限差分离散的一些重要结果.

在周期边界条件下考虑计算区间[xL,xR],其中网格尺寸h=网格点为Ωh={xj|xj=xL+jh,j=0,1,···,N −1}.记VN={v|v=(vj),vj ∈Ωh} ⊂RN为定义在Ωh上的网格函数空间,其离散内积和范数定义如下:

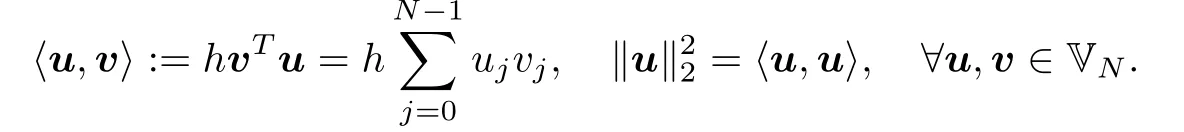
二阶拉普拉斯算子∂xx的中心差分矩阵记为

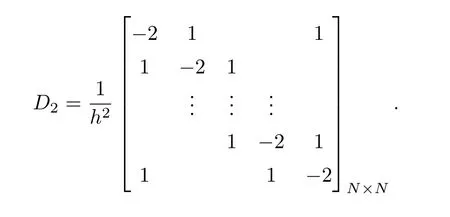
下面给出中心差分矩阵D2的一些基本结果.

引理1([18]) 关于矩阵D2,存在这样一种关系

令L=ϵ2D2.根据[19]的假设2,由离散矩阵L可以得到RN上的一个收缩半群,满足

其中∥·∥∞为矩阵的无穷范数.

注意到D2矩阵的所有行和都为0,我们有下面这条引理.

引理2([20]) 对于任意τ >0,总有=1.

引理3([20]) 对于矩阵L,有:

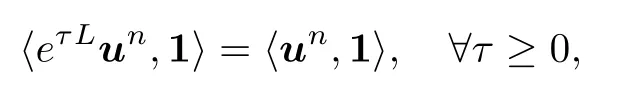
这里1=[1,1,···,1]T ∈RN.

一维空间下守恒型的Allen–Cahn 方程(2.1)可以写为如下形式:

运用文献[19]中的抽象框架,半离散系统(2.10)满足下面的极值原理:

定理2([19]) 考虑势函数为(2.4)的半离散系统(2.10).如果初值u0=u0(x)满足≤β,那么(2.10)的数值解u(t)满足离散极值原理

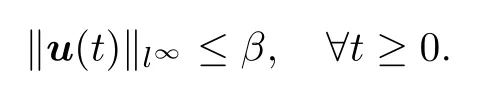
将离散质量和能量分别记为Mh(u)和Eh(u).分别对(2.10)的两边与1 和ut作l2内积并使用周期边界条件,可得到半离散系统(2.10)的质量守恒律:

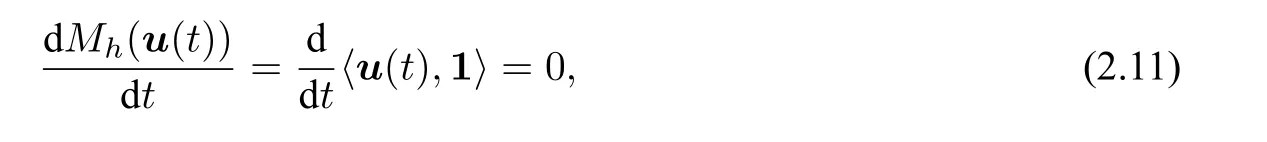
和能量耗散律:

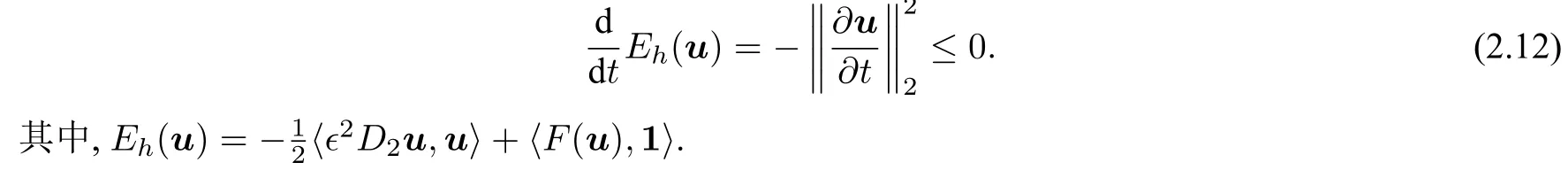
3 时间离散方法

本节结合时间方向上的积分因子两步Runge–Kutta 方法对半离散系统(2.10)构造全离散格式,并证明该格式可以保持质量守恒和极值原理.最后给出该格式的误差分析.

3.1 保极值的积分因子两步Runge–Kutta 格式

保持强稳定性(Strong stability-preserving,SSP) 的格式[21,22] 已经被广泛用来构造保极值的数值格式.本文将这种格式与积分因子两步Runge–Kutta 方法相结合,所得到的保持强稳定性积分因子两步Runge–Kutta(Strong stability-preserving integrating factor two-step Runge–Kutta,SSP-IFTSRK)格式可以在某种条件下保持(2.10)的极值原理和质量守恒.

Isherwood 等在[23]中开发并分析了一系列最高到八阶的带有优化SSP 系数的IFTSRK 格式.下面考虑一个带有SSP 系数C的s级p阶显式TSRK 格式,定义其Butcher 表如下:

其中ai,j=0(i ≤j),ci=,i=−1,0,···,s并且所有的系数都受精度和稳定性的限制.

在方程(2.10)的左右两边乘以e−Lt,可得到

因此,

应用变换w=e−Ltu到上面的方程,(2.10)化为:

将(3.4)与TSRK 结合,可得到如下的IFTSRK 格式:

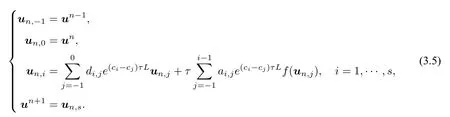
再将(3.5)重写为Shu–Osher 的形式[23]:

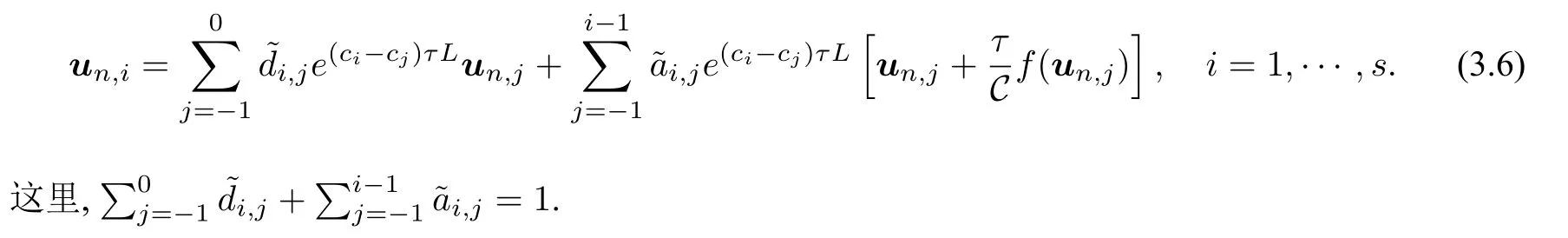
运用定理2,可以推导出下面的定理.

定理3假设使用到的TSRK 格式有非负的系数非减的节点ci和SSP 系数C.在条件τ ≤下,其中τF E表示满足

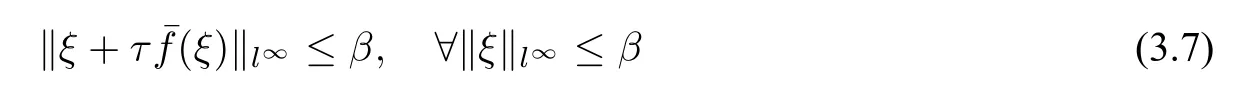
证明用数学归纳法来证明该定理.当n=0 时,结论是显然的.假设≤β,我们将验证对于un+1结果依然成立.

对于(3.6)的每一级,有

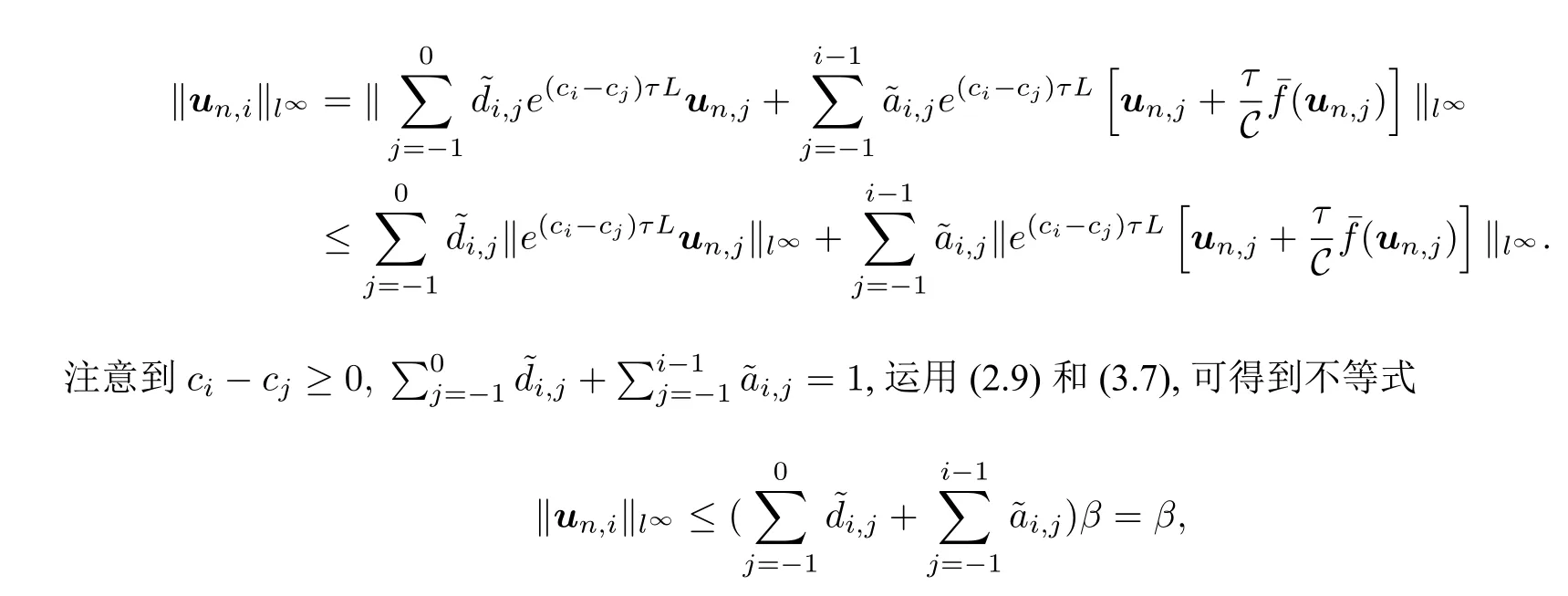
对于任何τ ≤都成立.定理得证.

下面给出SSP-IFTSRK 格式(3.5)保持半离散系统(2.10)质量守恒的定理及证明.

定理4假设TSRK 格式有非负的系数di,j和ai,j,非减的节点ci和SSP 系数C,那么在条件τ ≤CτF E下,SSP-IFTSRK 格式(3.5)可以保持守恒型Allen–Cahn 方程(2.1)的数值解的质量守恒律,即如果那么∀n>0.

证明同样用数学归纳法来证明定理的结论.对于守恒型Allen–Cahn 方程(2.1),有下式成立:

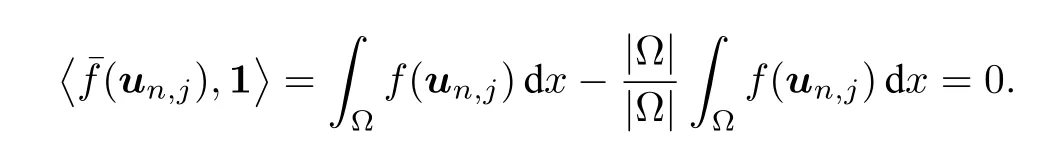
由〈un+1,1〉=〈un,s,1〉可知定理结论成立.

3.2 误差分析

本小节将建立关于守恒型Allen–Cahn 方程(2.1)的SSP-IFTSRK 格式在无穷范数意义下的数值解误差分析.为了简便起见,省略TSRK 方法的相关阶条件.通过使用定理3和s级p阶TSRK格式的定义,可以推导出如下的收敛结果.

定理5给定T >0,假设u(t)∈Cp[0,T]是半离散系统(2.10)的精确解,un是由SSP-IFTSRK方法(3.5)计算所得的数值解并且初值在[0,T]上充分光滑.在定理3的条件下,如果那么有误差估计

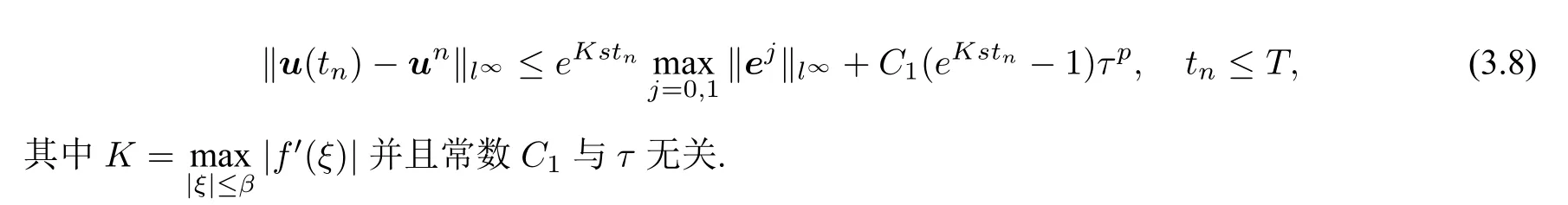
证明参考[15,24] 的证明方法,假设参考解为Un,i,−1≤i ≤s,其中,Un,−1=u(tn−1),Un,0=u(tn),Un,s=u(tn+1),且

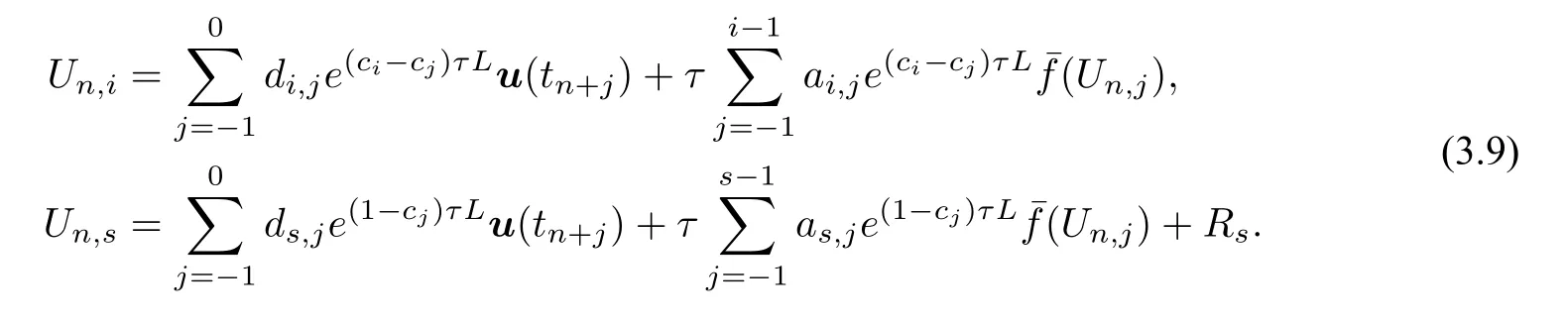
截断误差Rs满足

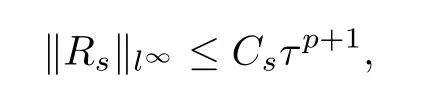
其中Cs与u的Cp+1[0,T]范数及f,s,p,T的Cp[−β,β]范数有关,但与τ无关.

令en+j=u(tn+j)−un,j,j=−1,0,en,i=Un,i −un,i,−1≤i ≤s,则en,j=en+j,j=−1,0和en,s=en+1.对于每个i=1,2,···,s −1,由(3.9)和(3.5)作差可得

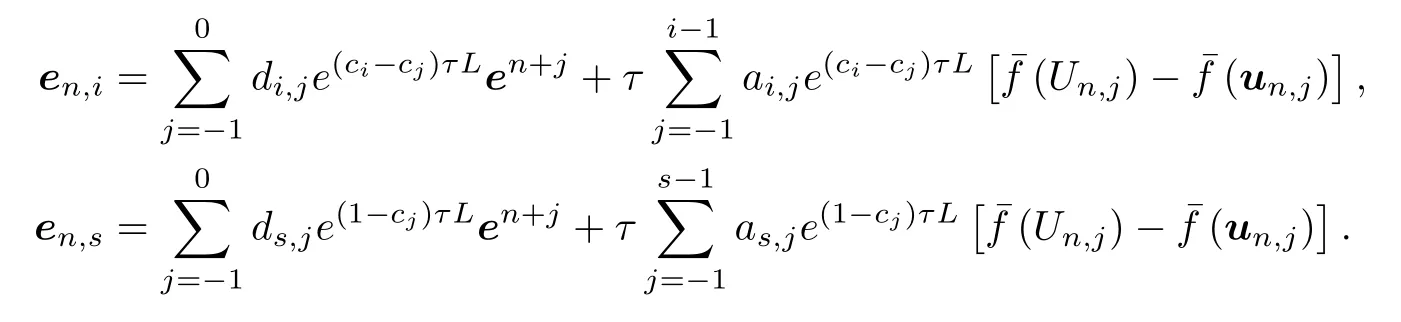
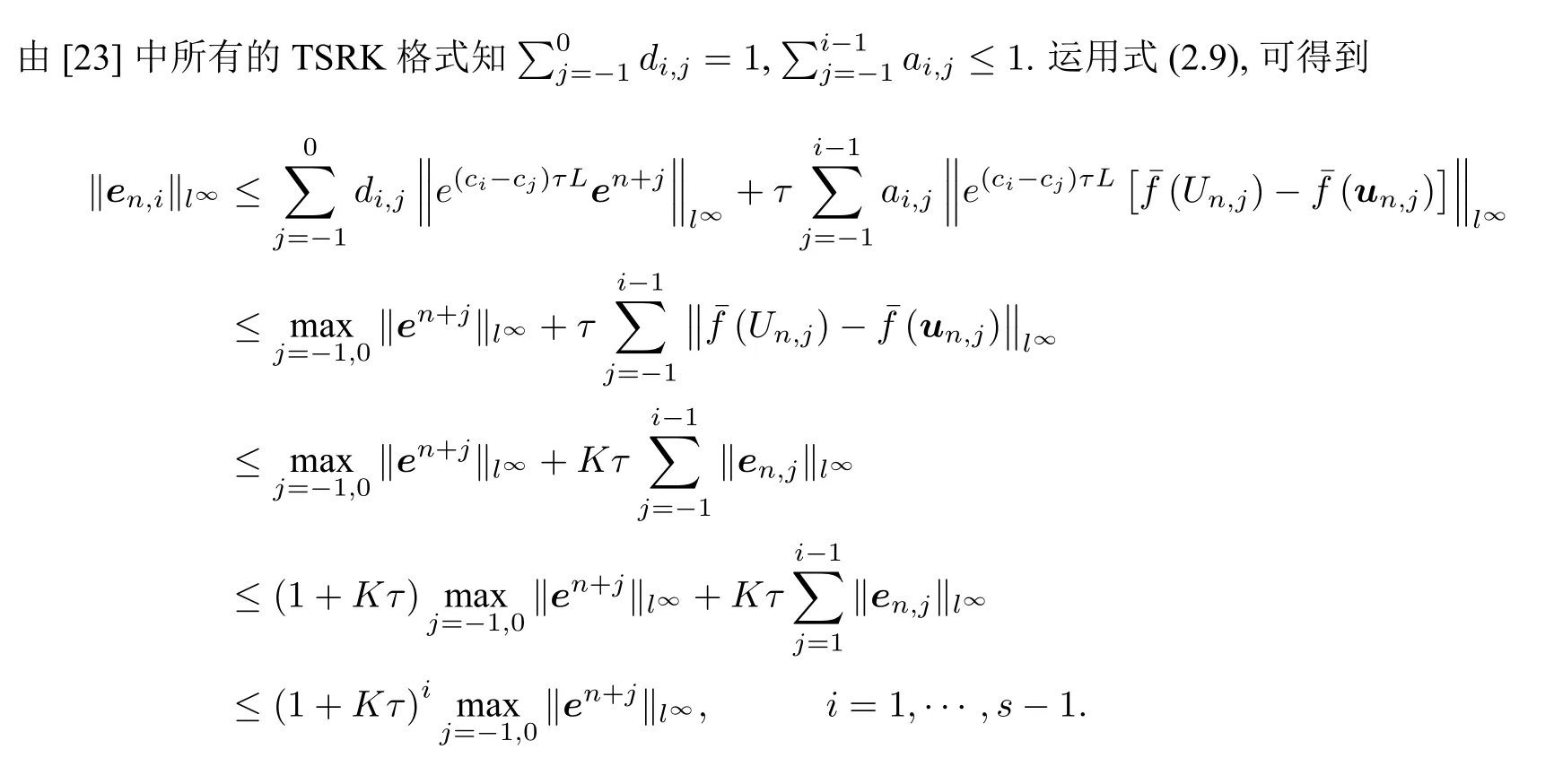
类似地,有

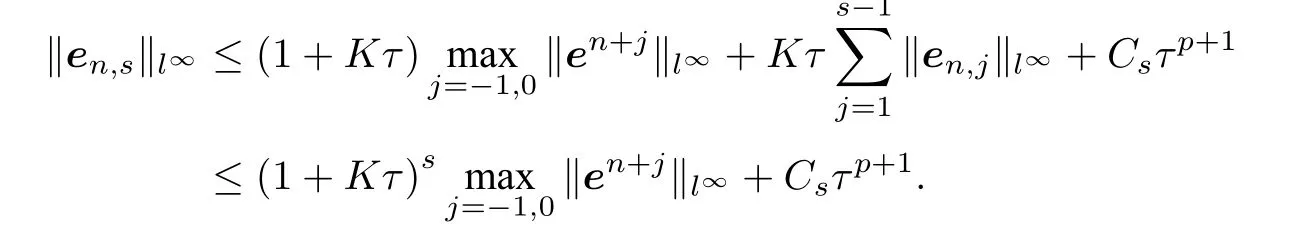
递归可得

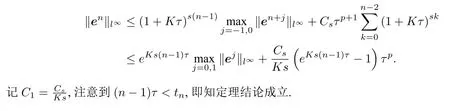
4 数值实验

本节首先介绍一些必要的准备工作,之后测试格式(3.5)的时间收敛阶,并且比较同一阶数下不同级数的情况.最后分别在二维和三维情形下模拟守恒型Allen–Cahn 方程的相变现象并且测试能量耗散性,保极值特性和质量守恒律.

4.1 准备工作

为便于之后的数值测试,将几种IFTSRK 方法和对应的SSP 系数列在表1 中.

表1 几个带有非负系数的优化SSP-IFTSRK(s,p)方法及其SSP 系数[23]

考虑带有周期边界条件的方程(2.1)时,d 维的DFT 技术可以应用到指数算子上.对任意的u ∈RN,算子可以重写为

其中F和F−1分别表示快速傅里叶变换(Fast Fourier transform,FFT)和它的逆变换,Λ由式(2.8)给出.

因为TSRK 方法不能自启动而且涉及到两个时间层上的变量,因此在用格式(3.5)进行数值测试前需要使用一个启动格式.该启动格式应满足两个条件:具有足够的精度和保极值特性.将第一个时间步一分为二后,使用SSPRK(5,4)格式或者SSPRK(10,4)格式作为第一个子时间步的计算,而第二个子时间步则用TSRK 格式进行计算.在之后的时间步里,只需用到时间层tn和tn+1对应的值un−1和un即可.

4.2 收敛阶测试

例1考虑以下一维初值条件[16]:

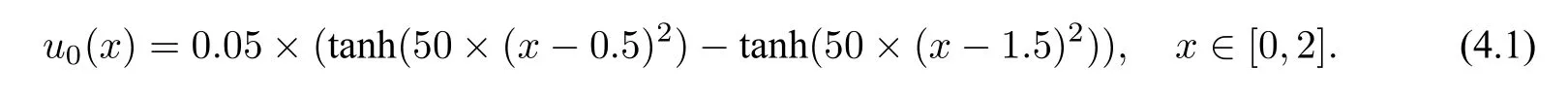
设参数ϵ=0.01,h=下面,计算时间步长为τ=2−k,k=0,1,···,8 的数值解.参考解则由时间步长取τref=2−12的SSP-IFTSRK(11,8)格式计算得出.图1的黑色虚线作为基准线用来表示理论阶的参考.

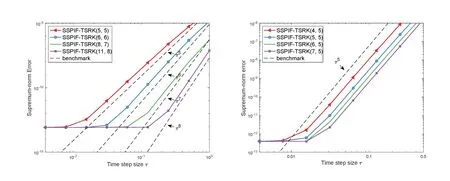
图1 T=2 时不同数值格式间的精度比较

图1 的左边展示出SSP-IFTSRK 格式从五阶到八阶的数值误差.四条线大致与基准线保持平行.图1 的右边则展示出同一阶数对应不同级数的收敛情况.实验与理论结果保持一致,即随着阶数增加,极值误差逐渐减少.

4.3 保结构测试

例2考虑常见的粘连气泡标准问题[25],其初值条件设置为

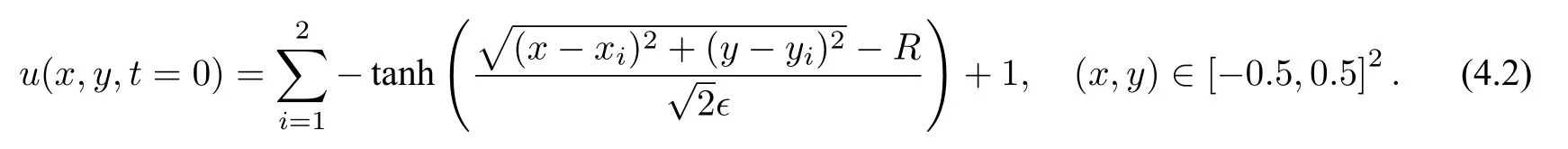
另外,半径R设置为0.19,(x1,y1),(x2,y2)分别设置为(0,0.2)和(0,−0.2),界面参数ϵ=0.01,时间步长τ=0.5,网格点数NX=NY=128.

使用经典AC 方程(1.2)和带有RSLM 形式的守恒型方程(2.1)分别计算该问题.选取级数较少的SSP-IFTSRK(4,5)格式进行测试.另外,选取6 个时间节点并在图2 展示出数值解的演化过程.图3 则展示对两个方程进行数值计算后得到的质量、极值和能量变化情况.在守恒型Allen–Cahn方程的极值图中我们添加一条黄色实线作为理论极值基准线,值为

从图2 可以看出,随着时间的推移,经典Allen–Cahn 方程对应的两个气泡从粘连到结合,变成椭圆后形状逐渐变小,最后在T=400 时彻底消失.而守恒型Allen–Cahn 方程对应的两个气泡在结合后并没有逐渐变小,形状却变得较为饱满,最后处于一个稳定的形态.这说明用SSP-IFTSRK格式可以很好地模拟出传质现象并且能直观地展示出两个不同方程间的差异.

从图3 可以看出,对于守恒型Allen–Cahn 方程,SSP-IFTSRK(4,5)格式能很好地保持质量守恒,同时极值也始终在理论值内,能量曲线单调下降.而对于经典Allen–Cahn 方程,可以看到质量曲线单调下降,极值与理论值1 保持一致,能量曲线单调下降且在最后时刻降为0.三个量的变化情况与图2 的演化过程是完全对应的,这也体现出所提出的数值格式的有效性和鲁棒性.

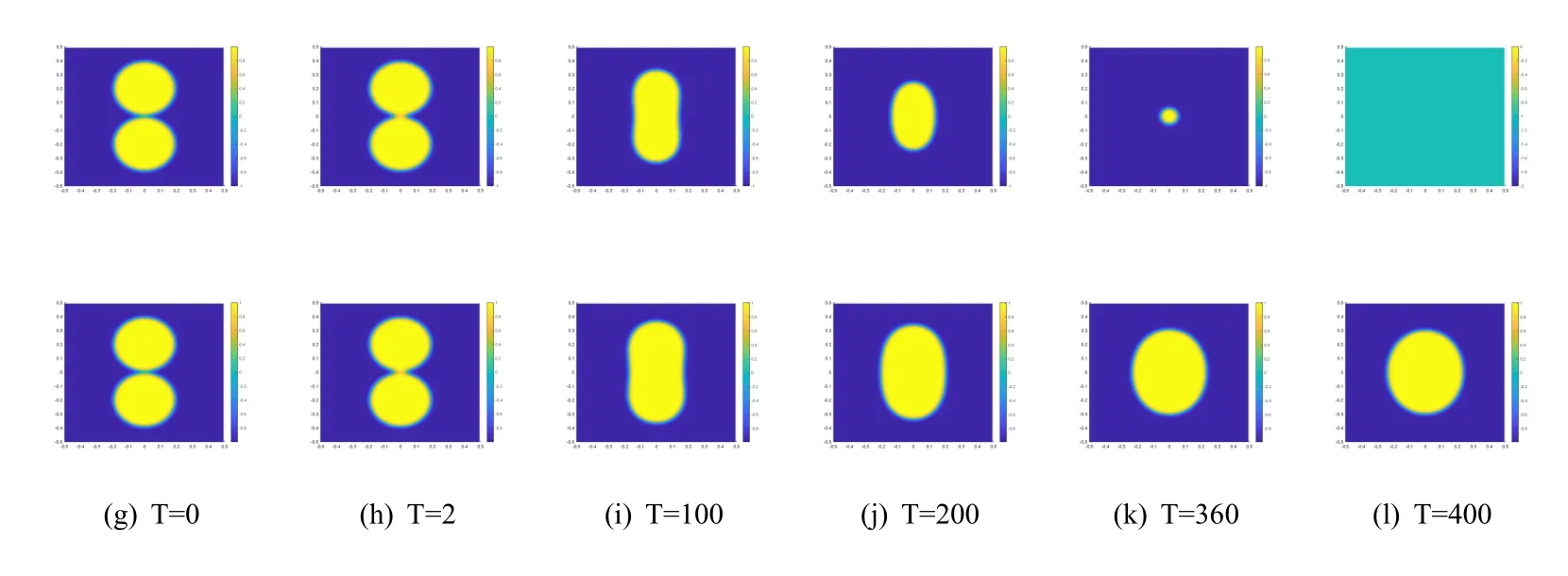
图2 使用SSP-IFTSRK(4,5)计算的粘连气泡数值解的演化过程.上半部分:经典Allen–Cahn 方程;下半部分:守恒型Allen–Cahn 方程

图3 使用SSP-IFTSRK(4,5)计算的粘连气泡的质量、极值和能量变化情况.上半部分:经典Allen–Cahn 方程;下半部分:守恒型Allen–Cahn 方程

例3考虑随机型三维初值问题:

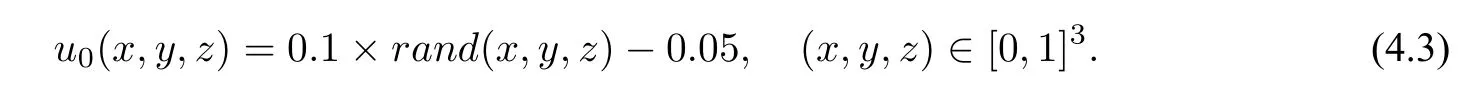
设置界面参数ϵ=0.01,网格点数NX=NY=NZ=128,时间步长τ=0.5.依然采用SSP-IFTSRK(4,5)格式对守恒型Allen-Cahn 方程(2.1)进行数值测试.选取6 个时刻来刻画两相分离的过程,分别为T=0,5,10,50,100,200.

数值解的演化过程在图4 中展示.可以看到,随着时间的推移,细小杂乱无章的相逐渐聚集并粗化,在T=200 时相的演化与初始时刻相比已经截然不同.

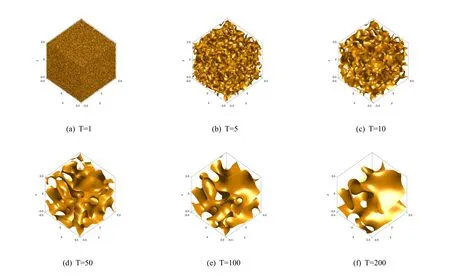
图4 使用SSP-IFTSRK(4,5)格式计算的三维随机型数值解的演化过程

整个过程的质量,极值和能量变化情况则在图5 中展示,其中黄色实线表示理论值可以看到质量是守恒的,能量曲线随着时间单调下降,而且极值原理也保持得非常理想.

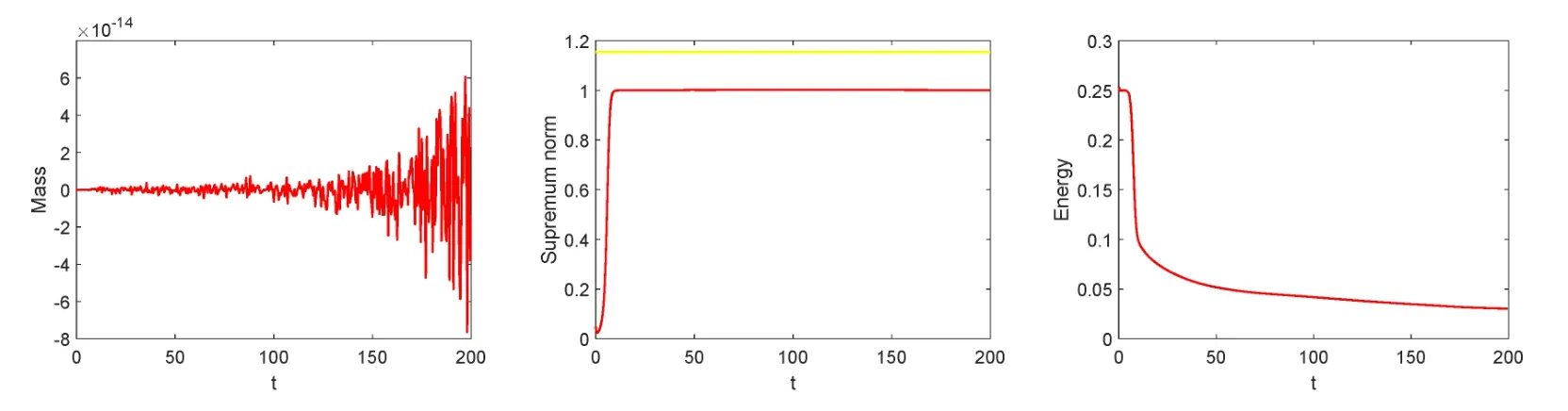
图5 使用SSP-IFTSRK(4,5)格式计算的三维随机型数值解的质量,极值和能量变化过程

5 结论

本文构造并分析了针对RSLM 形式的守恒型Allen–Cahn 方程的高阶保极值数值格式,并且分别从理论和实验两个方面证明了所提出的数值格式可以保持该方程的质量守恒,极值原理和能量耗散.数值结果也展现出所提出格式的一些优势,例如长时间稳定性、高效性和鲁棒性等.

注意到在使用SSP-IFTSRK 格式进行计算时,时间步长需满足不大于CτF E这一条件.因此如何消除这个条件使其能够无条件保极值原理,并且保持守恒型Allen–Cahn 方程的其他物理特性则是接下来要研究的目标.