Mean Field Equation on Spheres

Gui Changfeng Hu Yeyao Xie Weihong

(1.Department of Mathematics,The University of Texas at San Antonio,TX 78249,USA;2.School of Mathematics and Statistics,Central South University,Changsha 410075,China.)

Abstract In this expository note,we will introduce the recent progress and open problems concerning mean field type equations on spheres.In particular,some new inequalities of Aubin-Onofri type as well as their close connection to mean field type equations are presented.

Key words Mean field equation Paneitz operator Conformal metric Szegö limit theorem Moser-Trudinger inequality

1 Introduction

We consider the followingd-th order elliptic partial differential equation on Sd:

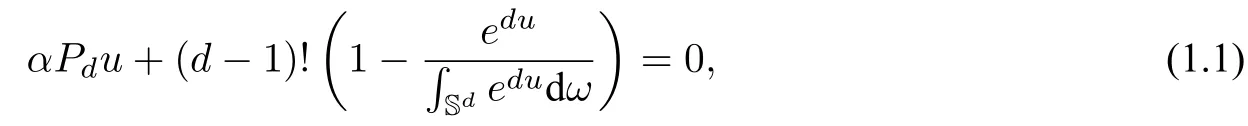
whereαis a positive constant,Pddenotes thed-th order Paneitz operator on Sdwith the standard metric and the volume form dωis so normalized that∫=1.Paneitz operators[87],or the so-called GJMS operators [40],could be understood as higher order generalizations of the conformal Laplacian in three or higher dimensional manifolds or Laplacian on two-dimensional surfaces,in the sense that all these operators exhibit conformal covariance property.In particular,Branson in[7]derived the explicit formula for the operatorPdon the standard unit spheres:

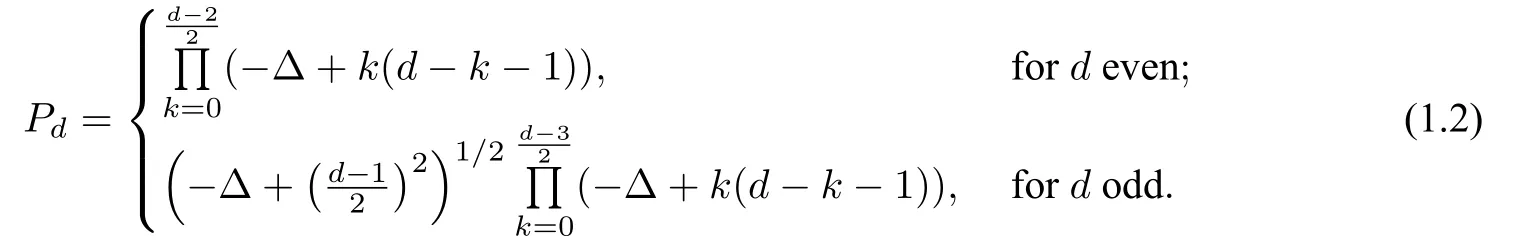
One might recall that the conformal Laplace operator gives rise to the prescribed scalar curvature problem,which is the problem of finding a metric that is conformal to the original metric such that the corresponding scalar curvature of the new metric agrees with a given function.In fact,if we denote the scalar curvature of a Riemannian manifold(M,g)with dimensiond ≥3 asRand consider a conformal deformationof metricgonM,the scalar curvatureunder the metriccan be expressed in terms of the conformal Laplacian

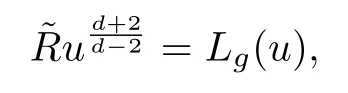
whereLg=is the conformal Laplacian on (M,g).The prescribed scalar curvature problem has been studied extensively since the pioneering work of Yamabe,and the problem of finding a conformal metric with a constant scalar curvature is also referred as the Yamabe problem.The interested readers are referred to[1,91,96,105]for literature on this topic.While for two dimensional surfaces,one should consider instead prescribing Gaussian curvature under the conformal change of metricand one can derive the following equation relating the Gaussian curvatureto the original curvatureK

Concerning(1.3),we provide here a list of references[11,12,18,21,22,27–29,31,35,53,65,66,69,71,75,83,84],which is far from complete.Note that the prescribing curvature problem posed on sphere is also known as the Nirenberg problem,see[63]and the references therein.

In [10],on a four dimensional manifold (M,g) Branson first defined the well known notion ofQcurvature

whereRicdenotes the Ricci tensor.Then,the celebrated four dimensional“analogue”of (1.3) is the following prescribedQcurvature equation:

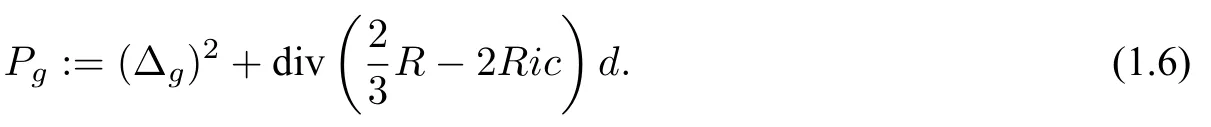
The Paneitz operator also appeared in the logarithmic determinant of conformal Laplacian in dimension four,see e.g.,[10,52,88,89].

Now we shift our focus back to the case on standard spheres,especially on S2.We taken=2 in both(1.1)and(1.2).Then,it is straightforward to verify thatP2=−∆and we get the two dimensional version of(1.1):

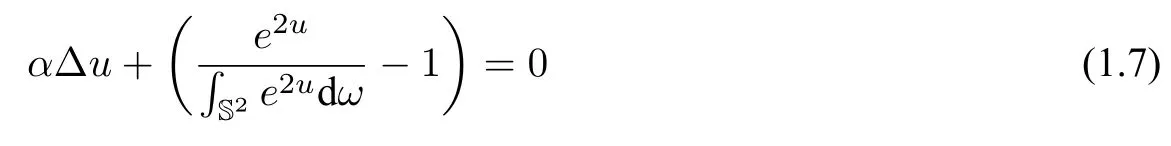
on S2.Equation(1.7)is termed“mean field equation”since the corresponding Dirichlet problem on planar domains arises as the mean field limit of vortex model of two dimensional turbulence,see e.g.[4,13–15,25,32,68].We will keep using the terminology“mean field equation”for(1.1)on spheres of all dimensions throughout the manuscript.

The survey is organized as follows.In section 2,we treat the“Paneitz operator”on S1.The classical Lebedev-Milin inequality[70]is revisited and the surprising connection between Szegö limit theorem[41]and one dimensional mean field equation is discussed.A PDE based proof of Widom’s observation is presented to better comprehend somewhat elusive connection between the two subjects.More precisely,A series of inequalities involving the exponentiation of functions on circle as well as their“momenta”with respect to higher order spherical harmonics is shown by classifying the solution of the mean filed equation on S1.In section 3,we focus on the two dimensional scenario.We state the Chang-Yang conjecture[21]and see its resolution in retrospect,especially the newest development made by the first author and Moradifam [44] via the sphere covering inequality approach.The dual form of the sphere covering inequality will also be presented.A recent novel inequality established by Chang and the first author in [17],which could be regarded as the first inequality in the theory of two dimensional Szegö limit theorem,is also presented.In section 4,some recent progress concerning (1.1) in four and higher dimensions is outlined.We will also mention some open problems and discuss possible ways to solve them along the lines.

2 Mean field equation and Szegö limit theorem on S1

In this section,we aim to give infinitely many inequalities which appear to be direct consequences of the Szegö limit theorem on S1and provide a proof of these inequalities using the one dimensional theory of mean field equation.

2.1 Lebedev-Milin inequality:a revisit

Milin in [70] discovered a classical inequality,which is now called the Lebedev-Milin inequality,concerning exponentiation of analytic functions while studying a folklore conjecture in geometric function theory,the Bieberbach conjecture.Let us recall the statement of Lebedev-Milin inequality.Assume that a complex functionusatisfyingu(0)=0 has the following power series expansion

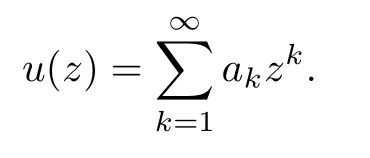
We also have a power series expansion foreu

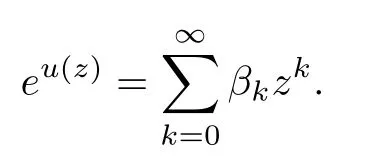
Then,we have

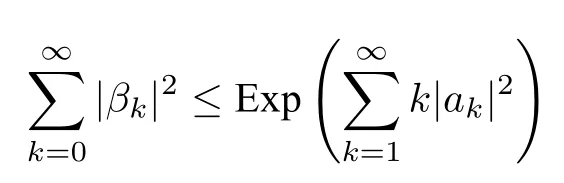
provided that ∑k|ak|2<∞and Exp(a) denotes the exponentiation ofa.The proof of this inequality employs the fact that(eu)′=euu′and the Cauchy-Schwarz inequality which we omit here.We now state the real form of the Lebedev-Milin inequality.

Theorem 2.1For anyu ∈consider the harmonic extensionofuinto the unit disk D1,thenand

wheredenotes the integral mean of functions on a measurable setA.

We will show that the above real form is equivalent to the original complex version of the Lebedev-Milin inequality.Without loss of generality,one may assume that=0.We expanduon S1:

One notes here thata0=0.Therefore,the harmonic extension ofucan be written as follows:

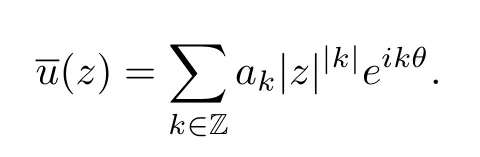
Sinceuis real,it is easy to check thata−k=Then,the harmonic conjugate functionvcan be expressed as

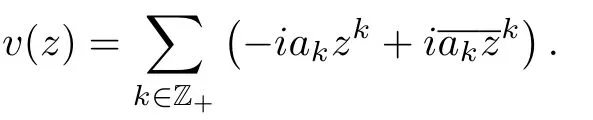
Letφ(z)=u+ivand we have

It is standard to check that

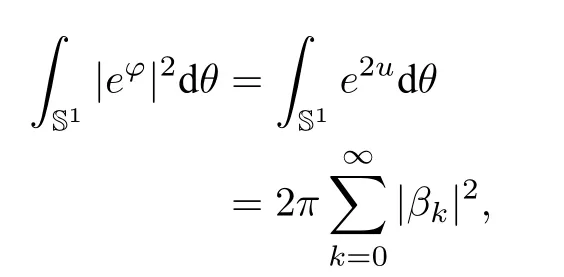
whereeφ=On the other hand,we also check that

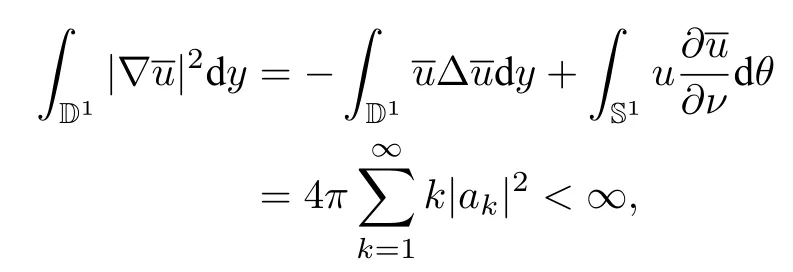
whereνdenotes the unit outward normal.The last inequality implies thatThus,by applying the complex Lebedev-Milin inequality toφand replacing 2uwithu,we arrive at the following inequality:

Recalling thatuis assumed to have zero mean,Theorem 2.1 immediately follows from the above inequality.

We can compare(2.8)with the(weak)Moser-Trudinger inequality on S2:Ifu ∈H1(S2),then

Therefore,the Lebedev-Milin inequality can be viewed as a Moser-Trudinger type inequality on S1.We will explain in details later in section 3 about Moser-Trudinger type inequalities.

2.2 Szegö limit theorem

The Szegö limit theorem was proved when Szegö studied the eigenvalue distribution ofn-th Toeplitz form.Toeplitz form is a special class of infinite-dimensional quadratic forms induced by matrices of infinite size.New orthogonal polynomials emerge in the theory of Toeplitz form.The study of Toeplitz form also leads to the concept of reproducing kernel,Bergman kernel,for example.Toeplitz form also has many applications in the field of probability and statistics.

We will introduce here a particular case of Szegö’s theorem which is adapted according to our setting.Before stating the theorem,we begin with the notions of Toeplitz matrix and Toeplitz determinant.Letf ∈L1(S1),then we can define the Fourier coefficients off

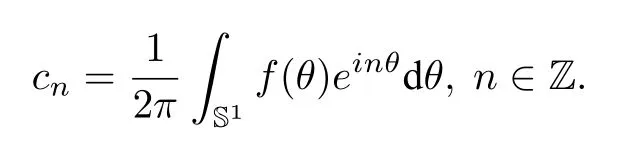
We define the infinite Toeplitz matrix as follows:

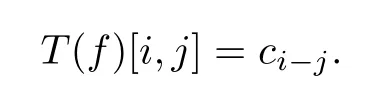
We also define then-th Toeplitz matrix as

The matrix representation ofTn(f)is:

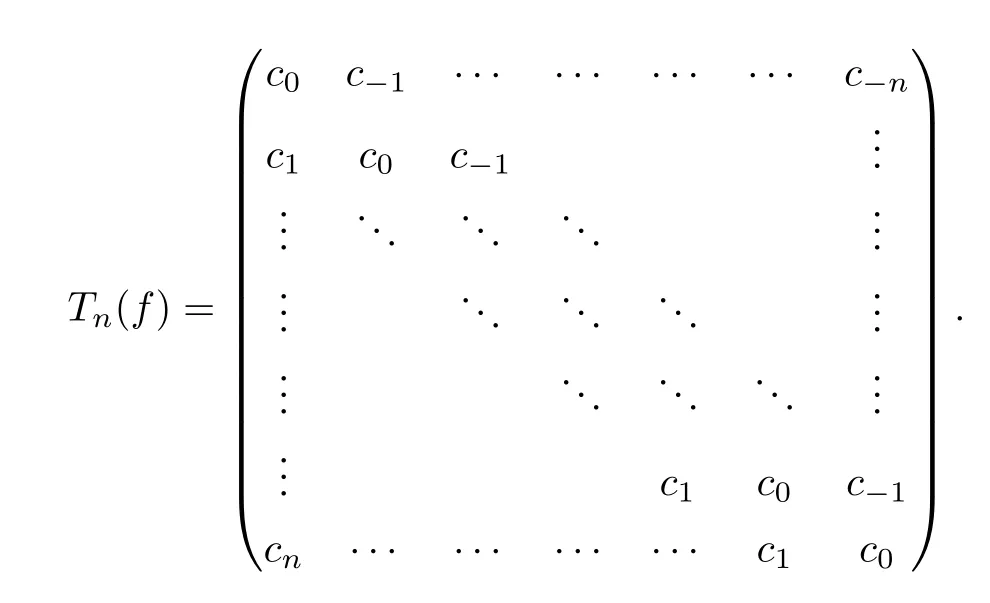
LetDn(f):=det(Tn(f))be then-th Toeplitz determinant.We are now ready to bring up the Szegö limit theorem which fits into our context.

Theorem 2.2([41]) Letu ∈Consider the Toeplitz determinantDn(eu),we have that the following sequence is non-decreasing with respect ton:

Furthermore,we also have the following limit:

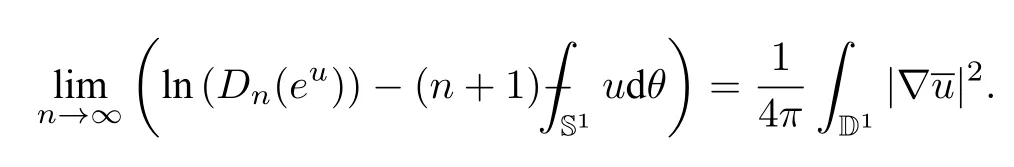
The idea of Szegö’s proof is to verify the Theorem for a special class of functions first,then a general function is approximated by these special functions and hence enjoys the same inequalities.Interested readers are referred to[41]for a complete proof.

It is fairly easy to compute that

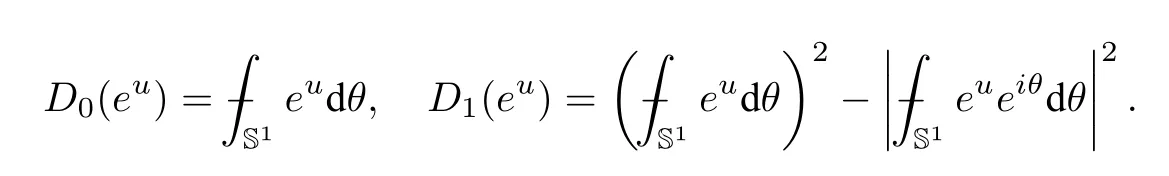
Therefore,Szegö limit theorem generates an infinite number of inequalities.Whenn=0,we have

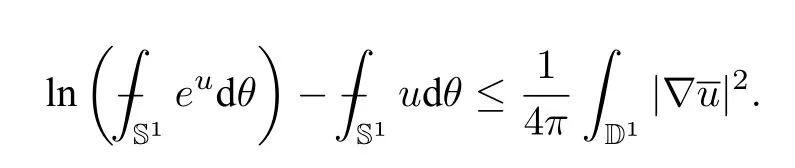
Whenn=1,we have

2.3 Widom’s observation:a PDE approach

We shall provide here a completely different proof of Widom’s observation using PDE techniques.In particular,we show that the one dimensional mean field equation on S1admits only constant solutions and then standard variational arguments lead naturally to(2.10).

In order to apply variational techniques,we need to rewrite the statements in section 2.2 by introducing the following functionals

where dωand dµare normalized measures of standard measures on D1and S1such thatω(D1)=1 andµ(S1)=1;and

Then,it is easy to see that the Lebedev-Milin inequality corresponds to the following property of theJα:

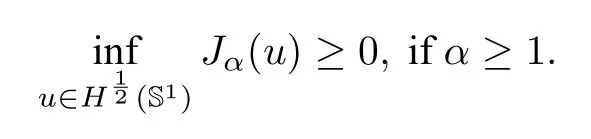
Similarly,the inequality(2.9)corresponds to

While Widom’s observation is equivalent to

where

In the two dimensional case,one can also consider the functionals of same nature which we also denote asJαandIα:

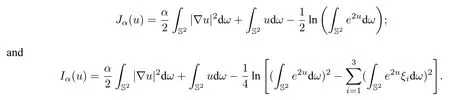
Here we abuse the notation a bit to denoteωas the normalized measure on S2so thatω(S2)=1.We will spend the whole Section 3 to address the two dimensional counterparts ofJαandIαwe just defined.Now let us first mention one remarkable progress recently made by Chang and Hang in[19].They showed that for a class of functions which have vanishing momenta up to ordern,there holds

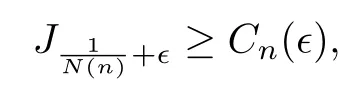
whereN(n)is a positive integer coming from the numerical quadrature formula on S2.They developed a concentration-compactness principle for mean field type equations and used it to prove their perturbative result.One notices that their methods could easily be adapted to one dimension and the integerN(n)=n+1 is exactly the smallest number of sampling points that is needed on S1to make the numerical quadrature formula work for polynomials of degree at mostn.Therefore,on S1there holds

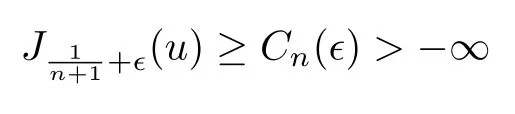
for anyu ∈Lnandϵ>0.So we can claim here that

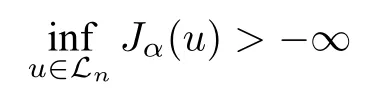
is attained and the minimizer exists for anyα>inLn.It is easy to verify that the minimizer satisfies the following Euler-Lagrange equation:

whereαkandβkare Lagrange multipliers with respect to the constraint that thek-th order momentum vanishes.By the celebrated Kazdan-Warner identity which will also be mentioned several times later,we can show thatαk=βk=0 for anyk=1,2,···,n.For a detailed proof of this fact in dimension one,the readers are referred to[19,Lemma 6.3].Then,the Euler-Lagrange equation becomes:

The above equation is considered as the mean field equation on S1.One notices thatcan be perceived as the Dirichlet-Neumann map of a functionu ∈and(2.13)can be rewritten as the following

Again recalling(1.1)and(1.2),one can easily check that whenn=1,P1=

Now we turn to classify the solutions of(2.13).

Theorem 2.3The mean field equation on S1(2.13) admits only the zero solution provided thatρ:=

The above theorem is first established by Osgood,Phillips and Sarnak in their famous paper [86].Here we present a proof by Wang[98].

ProofLetf=.Assume thatfcan be expanded as follows:

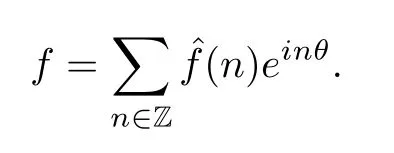
Thenucan be viewed as the harmonic extension offinto the unit disk D1:

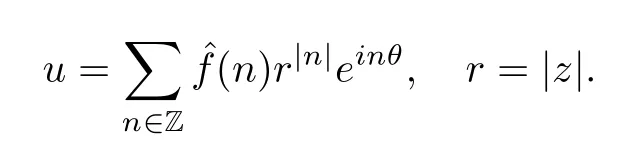
Therefore,

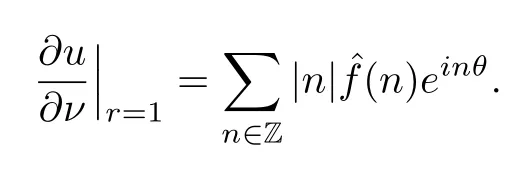
Now we recall the Hilbert transformH,for any

the Hilbert transform ofgis defined as follows:

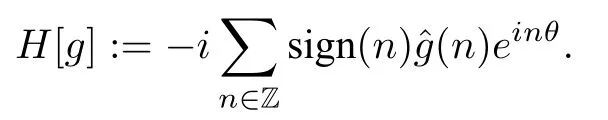
One can easily check that

Then we can representusing the notion of Hilbert transform:

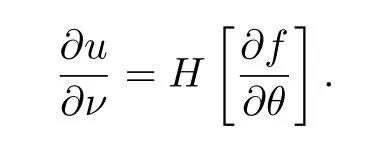
Therefore,(2.13)can be expressed in the following form:

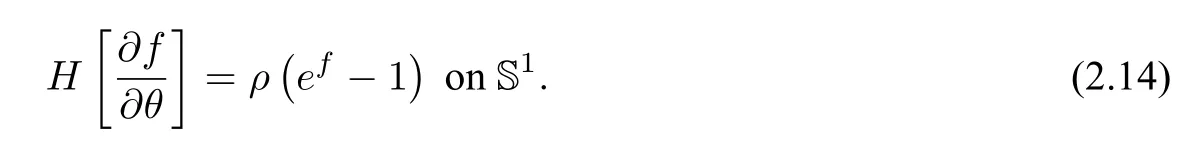
Equation(2.14)is nonlinear so one cannot use Fourier expansion to treat it.So we differentiate(2.14)byθboth sides.Noting that the Hilbert transform and differentiation commutes with each other,we get

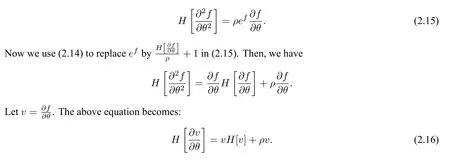
Now we can compare the Fourier coefficients of both sides of(2.16):

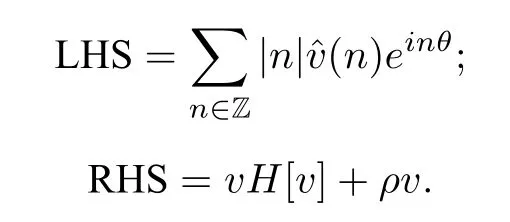
We can compute the first term on the right hand side of(2.16):

Therefore,combining the above equations,we have

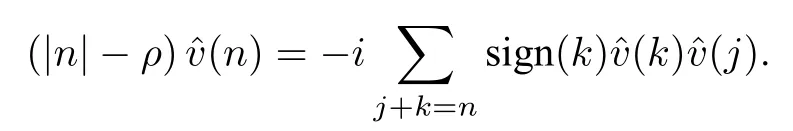
One can easily see that ifjandkhave opposite signs then by switching indicesj,k,then the sum among the ordered pairs(j,k)and(k,j)equals 0.Therefore,we have

Furthermore,it is easy to see that ˆv(0)=0 sincev=.Then,by induction,one can show that ˆv(n)=0 for alln ∈Z provided thatρ/∈Z+.Finally,we can conclude thatu=0.

For the critical caseρ ∈Z+,Wang proved in[98]that non-trivial solutions can be obtained explicitly.So far all the solutions of(2.13)have been classified and we have the following corollary.

Corollary 2.1(PDE proof of Widom’s observation)

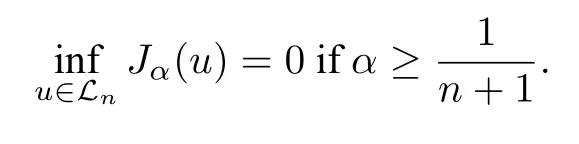
ProofFrom Theorem 2.3,it is easy to see that the only possible minimizers ofJαinLnshould be constant ifα>Then,we have

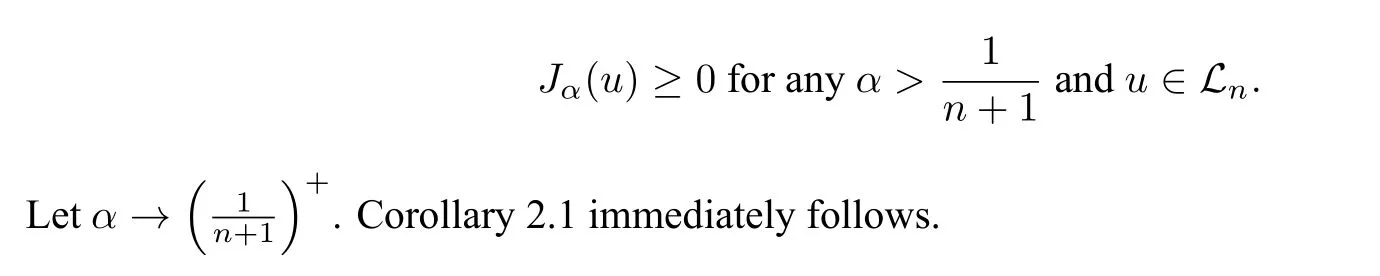
3 Mean field equation on S2

The main theme along the line in this section will be the resolution of Chang-Yang conjecture which was proposed in[21].The sphere covering inequality and its dual form are introduced together with some applications of the novel inequalities.Finally,a two dimensional“analogue”of the second inequality in the Szegö limit theorem is also stressed.

3.1 Moser-Trudinger-Aubin-Onofri type inequalities

We start with the eminent Moser-Trudinger inequality[82,95].Let(M,g)be a closed surface,then for anyu ∈H1(M)such that0,=0,we have

where dωdenotes the measure induced by the area element of(M,g)andc(M,g)denotes a constant which is only dependent on(M,g).This classical inequality has its weak form on the standard sphere S2which can be written in terms of the functionalJαdefined in Section 2:

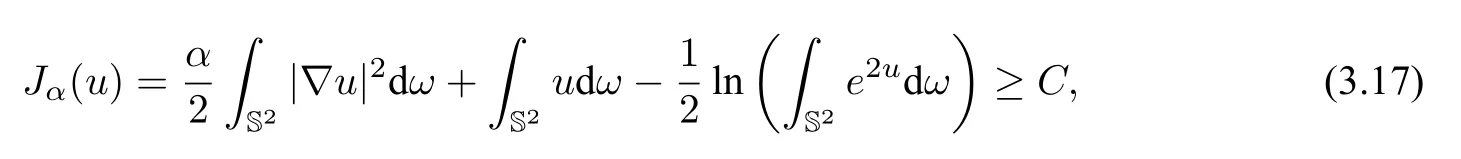
forα ≥1 andu ∈H1(S2).One notes thatα=1 is sharp in the sense that (3.17) fails ifα <1.One shall also notice that the 4πconstant in the Moser-Trudinger inequality corresponds to the critical parameterα=1.It is remarkable that 4πis optimal,i.e.,the Moser-Trudinger inequality does not hold if 4πis replaced by a constant greater than 4π.Moser-Trudinger type inequalities have a very wide range of applications in the study of partial differential equations with exponential non-linearity.Many mathematicians exploited Moser-Trudinger inequalities to make notable contributions to the blow-up analysis of Liouville type equations,among them are Brezis,Li and Merle[11,12,71].In[2],Aubin studiedJαunder the constraint that the mass center ofe2uis at the origin and found that(3.17)can be improved toα ≥under this constraint.Onofri in[85]showed that the lower bound ofJαonH1(S2)is 0 ifα ≥1 based on Aubin’s fundamental work and conformal covariant property of the functional.Chang and Yang in[21]pushed theαto some number slightly below 1.They proposed a conjecture in the same paper.

Conjecture 3.1(Chang-Yang conjecture) For anyα ≥andu ∈H1(S2)satisfying:

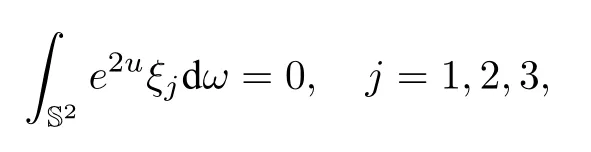
we have

whereξ=(ξ1,ξ2,ξ3)∈S2⊂R3.

Among the other things,Chang and Yang also proved that the minimizer exists forJαunder the mass center constraint.Moreover,the minimizer solves the following Euler-Lagrange equation:

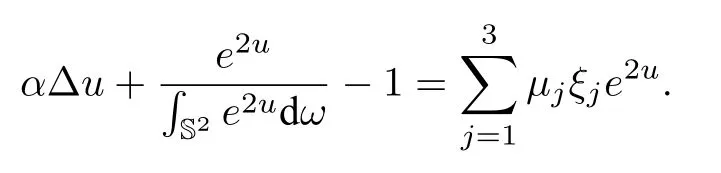
By the same Kazdan-Warner obstruction previously mentioned in Section 2,the Lagrange multipliersµjmust be zero to ensure that the above equation has solutions.Thus,we deduce the two dimensional mean field equation on S2(1.7).

Conjecture 3.1 drew a lot of attention of a vast number of PDE analysts ever since its publication.Feldman et.al.in [36] found that (1.7) admits only constant solutions whenα >−ϵ(ϵis some small positive constant) if axially symmetric functions are considered.Thus,they actually improved the Aubin-Onofri inequality to someαslightly belowfor axially symmetric functions.The sharp Aubin-Onofri inequality for axially symmetric functions is independently substantiated by two groups of mathematicians.The first author and Wei in[51],Lin in[74]proved that whenα ≥Jα(u)≥0 holds for allu ∈H1(S2)that satisfies the condition on the mass center.Later,Ghoussoub and Lin in[37]confirmed the conjecture whenα >−ϵfor general functions without assuming the axially symmetryness.More recently,the first author and Moradifam in[44]provided a complete resolution of Conjecture 3.1 which has remained open for more than thirty years.They invented a brand new tool,the sphere covering inequality,and utilized this new tool to show that(1.7)admits only constant solutions ifα ≥andα1.

3.2 The sphere covering inequality and beyond

As we can see from the previous section,the sphere covering inequality plays a rather vital role in confirming Chang and Yang’s long-standing conjecture.It provides another way of proving the symmetry of solutions to various Liouville type equations and certainly has many applications in classifying the solutions of mean field type equations.We plan to present both the original version of the inequality and its dual form.Some of the applications to other related problems will also be covered.

Theorem 3.1(The sphere covering inequality[44]) Let Ω be a simply connected region of R2and assume thatvi ∈i=1,2 are the solutions of the following equations:

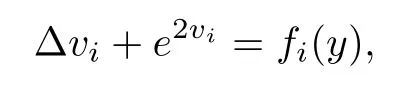
wheref2≥f1≥0 in Ω.Assume further thatv2≥v1,v12andv1=v2on∂Ω,then

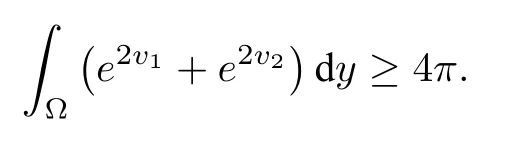
Moreover,the equality holds only whenf1≡ f2≡0 andare isometric to two complimentary spherical caps on the unit sphere.

Consider the limiting casev1≡v2and we drop the subscript ofvfor simplicity,one has the following inequality:

Theorem 3.2([3,37,76,78]) Let Ω be a simply connected region of R2andv ∈such that

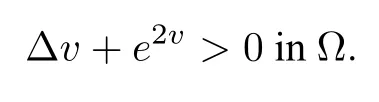
Assume that there exists someφ ∈such that

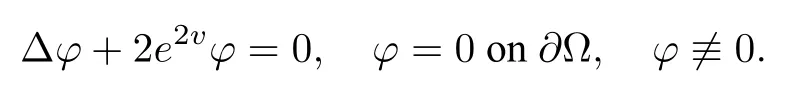
is a solution of the equation in Theorem 3.2.Hence,one can derive the conclusion of Theorem 3.2 by the sphere covering inequality and sendingk →∞.Interested reader is referred to[44]for rigorous proofs of the two theorems.One shall also note here that in [37] Ghoussoub and Lin used the stereographic projection to transform(1.7)to an equation on R2.They studied the nodal domains of a specific solution to the linearized equation and applied Theorem 3.2 to confirm the Chang-Yang conjecture forα ≥Nevertheless,the first author and Moradifam in [44] did the nodal line analysis on sphere and then apply Theorem 3.1 to finally resolve the conjecture.The study of mean field type equations has become a very active topic and progress has been made ever since Theorem 3.1 was purported.Among the fruitful achievements,we would like to mention that another long-standing conjecture by Lin [77] on the uniqueness of solutions to the mean field equation on flat torus was also solved in[42]via a successful application of Theorem 3.1.One is referred to [5,43,45,46,97] and the references therein for recent developments in this direction.

In [47],the first author,Hang and Moradifam discovered the dual form of the sphere covering inequality.They also gave a new way of understanding the sphere covering inequality in the prospect of comparison geometry.We first present here a generalization of the sphere covering inequality.

Theorem 3.3([47]) Let Ω⊂R2be a simply connected region.Assume thatu1∈such that

Let Ω′ ⊂Ω be a bounded region.Assume thatu2∈and 0<λ ≤1 such that

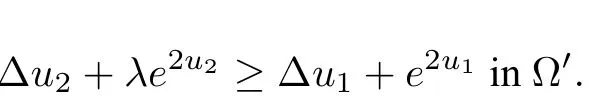
Assume further thatu2≥u1,u12andu1=u2on∂Ω′.Then

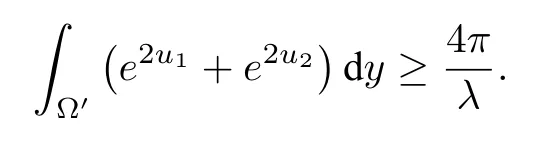
We also give the dual form of the sphere covering inequality.

Theorem 3.4([47]) Let Ω⊂R2be a simply connected region.Assume thatu1∈such that

Let Ω′ ⊂Ω be a bounded region.Assume thatu2∈such that

Assume further thatu2≤u1,u12andu1=u2on∂Ω′.Then

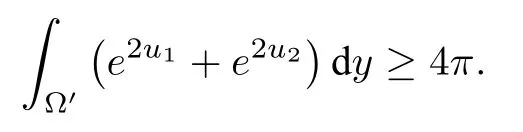
The proofs of Theorem 3.3 and Theorem 3.4 involve the general form of Alexandrov-Bol’s inequality and thus rely on the upper bound condition of the Gaussian curvature.However,the first author and Moradifam validated Theorem 3.1 by rearrangement argument and the radial version of Bol’s inequality.More general theorems concerning similar inequalities on two dimensional surfaces are included in their paper[47]as well as possible applications of those inequalities on mean field type equations on manifolds.

3.3 Two dimensional Szegö limit theorem

In section 2,we proved Widom’s observation (2.10) using PDE methods.A natural question then arises:is there any analogue of (2.10) on S2? In this direction,Chang and Hang in [19] obtained an“almost”optimal inequality on S2which we have already brought up in section 2.Here,we elaborate the result in more details:letPn:==0:pis a polynomial with degree at mostn,then for any functionu ∈H1(S2) that satisfies∫=0 and an arbitraryϵ >0,we have the following inequality

whereN(n)denotes the smallest number of sampling points that is needed on S2to make the numerical quadrature formula work for polynomials of degree at mostn.One shall note here that the corresponding constantN(n)=n+1 on S1as we stated in section 2 but the same problem remains open on S2except only a few cases whennis very small,see e.g.[19].One shall also see that the orthogonal conditions we introduce in this section are equivalent to the vanishing momentum conditions we defined in section 2.Their paper unearthed somewhat obscure connection between mean field equation and spherical design problems in combinatorics.

We can rewrite the inequality≥0 according to the one dimensional Szegö limit theorem as follows:

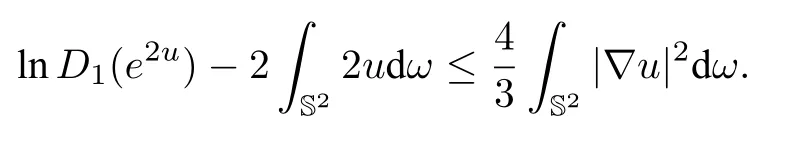
One shall note that the corresponding constant on the right hand side of the above inequality is 1 in the one dimensional scenario.One can see the essential difference between the one dimensional case and higher dimensional cases from this fact.We can now recognizeJ1(u)≥0 as the first inequality of the two dimensional Szegö limit theorem while≥0 can be regarded as the second inequality of the two dimensional Szegö limit theorem.

Although much has been fully understood,there are still unclear questions in dimension two.Here we list some problems which remain open so far.Concerning the classification of solutions to(1.7),a series of fundamental work settles the problem for the parameter rangeα ∈∪(1,∞),i.e.,it is proved that the only solutions of(1.7)are constants.For other ranges ofα,we propose the following conjectures.

Conjecture 3.2Forα ∈,all solutions to(1.7)are axially symmetric.

The range of parameter cannot be extended toαbelowsince non-axially symmetric blow up solutions can be constructed ifα →In fact,blow-up phenomena could occur whenα →for any positive integern ≥2,see e.g.,[48].

Conjecture 3.3Forα ∈,non-trivial axially symmetric solution to (1.7) is unique up to constant.

Concerning the two dimensional version of Widom’s observation,the first author and Moradifam in [44] verify the casen=1 which is exactly the Chang-Yang conjecture.Then,one might ask if the corresponding inequality whenn=2 is true on S2.One shall note thatN(2)=4 is known for S2,please see[19]for more details.Another natural question one could ask is if there is a version of the Szegö limit theorem on S2forn ≥2 for the Toeplitz determinantDn(e2u).We suggest that maybe one consider the axially symmetric case first for both two problems we just mentioned.

4 Higher dimensions

In this section,we consider the mean field equation in higher dimensions.We recall(1.1)and(1.2):

where

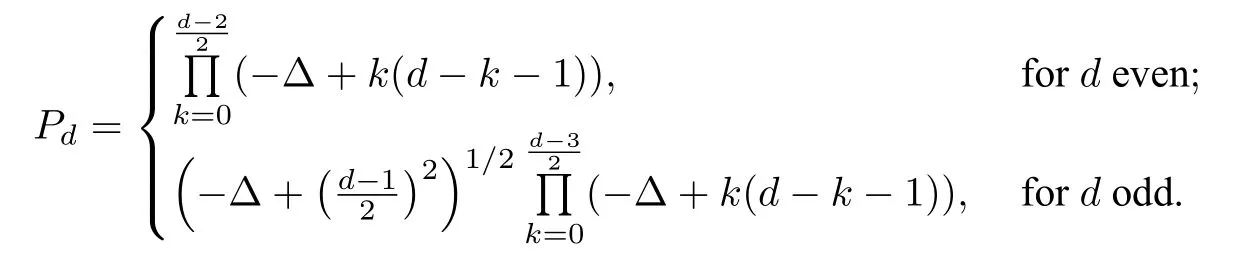
The caseα=1 is also called the constantQcurvature equation on Sd.The corresponding functional is defined inby

Beckner in[6]established the following Beckner’s inequality(a higher order Moser-Trudinger type inequality):

Furthermore,J1is invariant under the conformal transformation

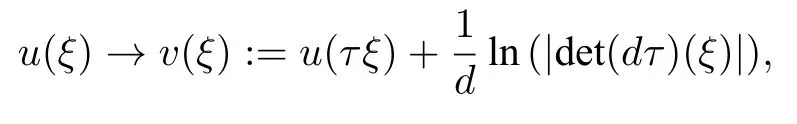
whereτis an element of the conformal group of Sdand|det(·)|is the modulus of the corresponding Jacobian determinant.Equality in(4.18)is only attained at functions of the form

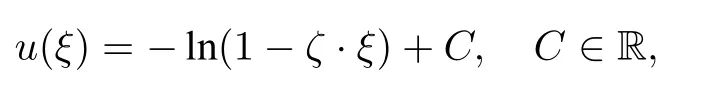
whereζ ∈Bd+1:={ξ ∈Rd+1,|ξ| <1},see also [23].In particular,(1.1) has a family of axially symmetric solutions

Since(1.1)is invariant under addition by a constant,we can normalizeuso that=1.Then,(1.1)can be written as

Let Π be the stereoprojection from Sdto Rd,[8,Theorem 3.3]indicated thatPdis the pull back under Π of.Thus,by settingα=1,we find the corresponding equation on Rd:

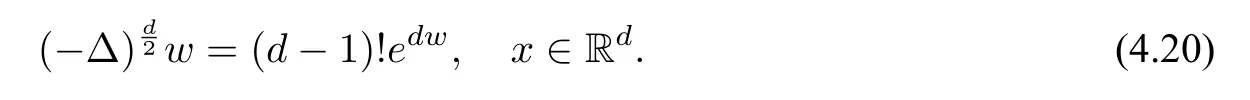
Chang and Yang[24]proved the following classification result:

Theorem 4.1([24,Theorem 1.2]) On Rd,suppose a smooth functionwsatisfies(4.20)and

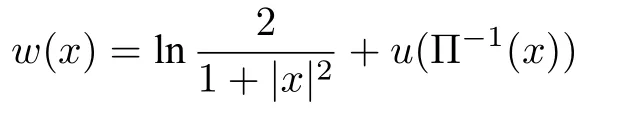
with some smooth functionsudefined on Sd,thenw(x)is symmetric with respect to some pointx0∈Rd,and there exists someλ>0 so that

Letγ=In the special case ofd=4,Lin in[73]also obtained solutions in the form of(4.21)under more general conditions:

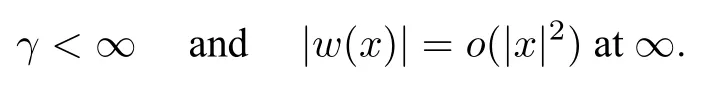
Such a result was independently established by Xu[103].Moreover,Lin proved the symmetry result as follows.

Theorem 4.2([73,Theorem 1.2]) Letγ <∞andwbe a solution of (4.20) on R4.Then the following statements hold.

(i)After an orthorgonal transformation,wcan be represented by

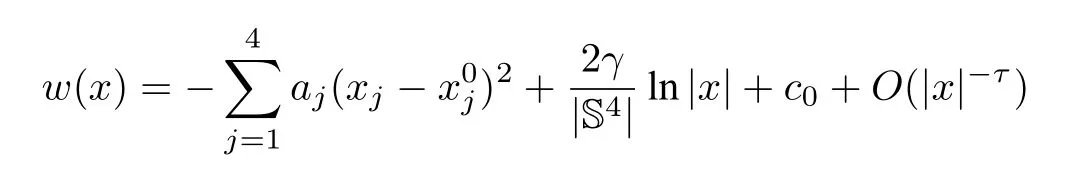
for someτ >0 and for large|x|,whereaj ≥0,c0are constants andx0=∈R4.Moreover,ifai0 for alli,thenuis symmetric with respect to the hyperplaneIfa1=a2=a3=a40,thenuis radially symmetric with respect tox0.

(ii)The total integrationγ ≤|S4|.Ifγ=|S4|,wtakes the form of(4.21).

Subsequently,Wei and Xu in[100]generalized the above theorem to all even dimensions.Recall that Chen and Li [26] showed that whend=2,all solutions to (4.20) withγ <∞are radially symmetric with respect to one point and have the form(4.21).We conclude that the classification result to(4.20)in dimension two is very different from those in other even dimensions.In this direction,we refer interested readers to[16,57–62,64,80,81,101,104]for other cases.

On the other hand,Chang and Yang in[23]considered the constantQcurvature type problem.They studied the functionalJαand established an improved Aubin-type inequality,see[23,Lemma 4.6].

For anyα >1/2,there exists a constantC(α)≥0 such thatJα(u)≥−C(α) wheneveru ∈L.Here L denotes the set of functions with center of mass at the origin,i.e.,

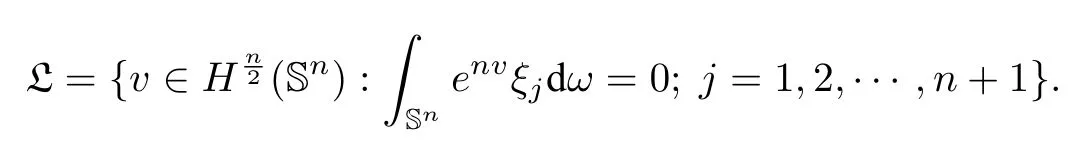
This gives rise to the existence of a minimizer ofJαin L and the minimizer satisfies the corresponding Euler-Lagrange equation

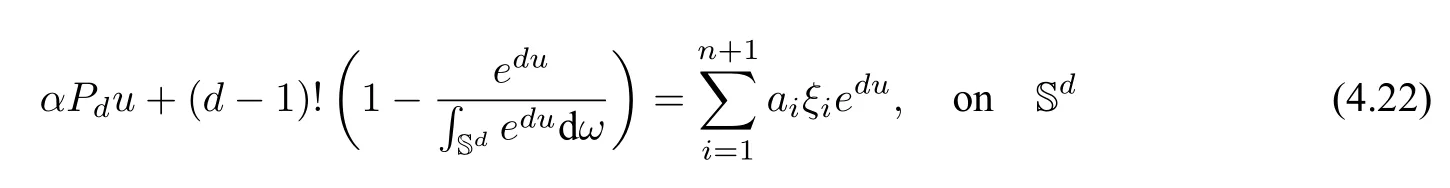
for some constantsai,i=1,2,···,n+1.Furthermore,it has been shown in[23,Remarks(3)(ii)for Cor.5.4]that the following Kazdan-Warner condition

is also applicable for the prescribedQcurvature equation

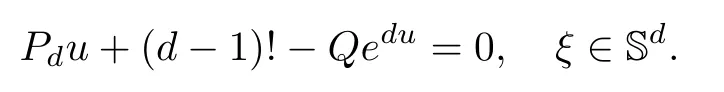
It is an immediate consequence thatai=0,i=1,2,···n+1,in(4.22).This argument is reminiscent of that in [21,Cor.2.1] on prescribed Gaussian curvature type equation,or the mean field equation on S2.Interested readers are also referred to[20,33,34,55,56,72,79]for literature on equations that have conformal structures.

Different from [24],Wei and Xu in [99,Cor.2.5] used conformal vector field to get the Kazdan-Warner result(4.23).Moreover,they also confirmed an improved Beckner’s inequality:

Proposition 4.1There exists a constantα<1 and close to 1 such that

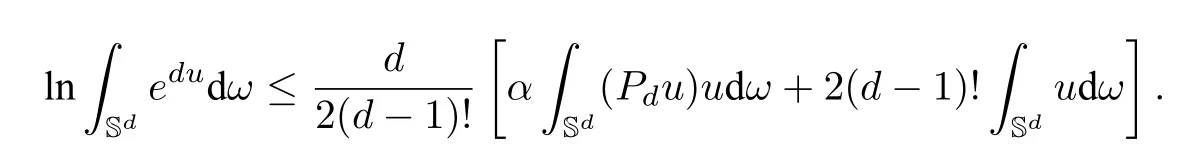
In [49,50],we considered axially symmetric functions only dependent onξ1to treat (1.1) in high dimensions.Precisely,we proved that(1.1)admits only constant solutions whenαbelongs to some suitable sub-interval of[1/2,1).As a consequence,we established an improved Aubin-type inequality for axially symmetric functions.

Considering solutions that are axially symmetric aboutξ1-axis and denotingξ1byx,(1.1) can be reduced to

Then the following results are obtained.

Theorem 4.3([49,50]) Letd=4,6,8.Ifα(d)≤α<1,then(4.24)admits only constant solutions.As an immediate consequence,we have

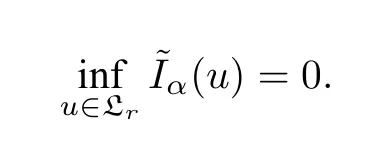
We believe thatJ1/2(u)≥0 foru ∈L,given the similar inequality for S2as shown in [44].We define the following functionals on

Note thatIα(u)=Jα(u)whenu ∈L.As a consequence of Theorem 4.3,we had the following form of the first Szëgo limit theorem on Sdfor axially symmetric functions.

Theorem 4.4([49,50]) Letd=4,6,8,then

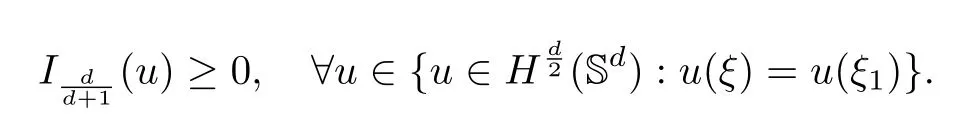
The authors focused on (1.1) withd ≥3 in the axially symmetric setting.The following result classifies axially symmetric solutions of(1.1)at the critical parameterα=

Theorem 4.5([50]) Ifα=anduis an axially symmetric solution to(1.1)withd ≥3,thenumust be constant.

Note that the cased=2 was settled in[93].

Moreover,we also established the following proposition concerning the centers of mass and the first order“momentum”of solutions to(1.1).

Proposition 4.2([50]) Ifusolves(1.1),then

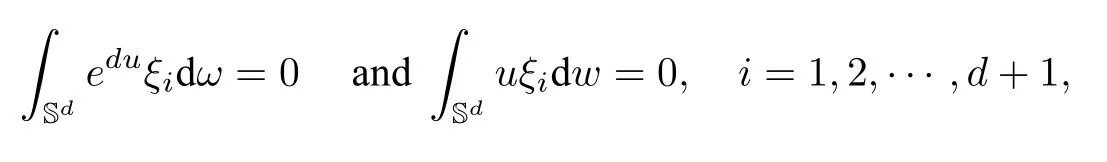
wheneverα1.

Using a bifurcation approach and Theorem 4.3-4.5,we proved the existence of non-constant axially symmetric solution forα ∈

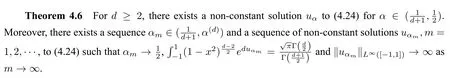
We conjectured in[49]that the uniqueness result of Theorem 4.3 should hold for≤α<1 and all dimensions.Indeed,the lower boundcan be improved slightly to 0.5145 in dimension four by some technical improvements which did not suffice to get the optimal bound

Here we list some open problems:

(1)Can one show that the solutions to(1.1)are axially symmetric provided thatα ∈[,1),possibly by using a higher dimensional sphere cover inequality?

(2)Using the conformal covariance property of the Paneitz operator,it is well known that the high dimensional mean field equation could be written as an equation involvingon Rd.LetK(x)=(1+|x|2)l.Can we classify the solutions to

with a given total curvature

for a suitable range ofl>0? In particular,l=corresponds to(1.1).

(3)Is there a connection between(1.1)and isoperimetric inequalities with curvature conditions in high dimensions? Note that one can easily relate the two dimensional mean field equation to the Alexandrov-Bol inequality.