Unique Continuation from a Vertex Corner for Maxwell’s System

Diao Huaian Liu Hongyu Zhang Long

(1.School of Mathematics,Jilin University,Changchun,Jilin 130012,China;2.Department of Mathematics,City University of Hong Kong,Hong Kong SAR 999077,China;3.Fengcheng No.1 Middle School,31 Zhenxing St,Fengcheng,Dandong 118100,China）

Abstract In this paper,we establish a novel unique continuation property (UCP) for the Maxwell system locally around a vertex corner.It is shown that if certain homogeneous conditions are imposed on the planes forming the vertex corner,the electric/magnetic field must vanish to a certain order.We derive the vanishing order and relate it to the polyhedral angles of the vertex corner.This extends the recent results in[21]where the UCP was considered associated with an edge corner.This type of UCP study originated from the study of a longstanding problem in inverse scattering theory.

Key words Maxwell system Time-harmonic electromagnetic scattering Unique continuation Vanishing order Vertex corner Inverse scattering A single far-field measurement

1 Introduction

1.1 Mathematical setup

Initially focusing on the mathematics,but not the physics,we first present the mathematical formulation of our study.

Let

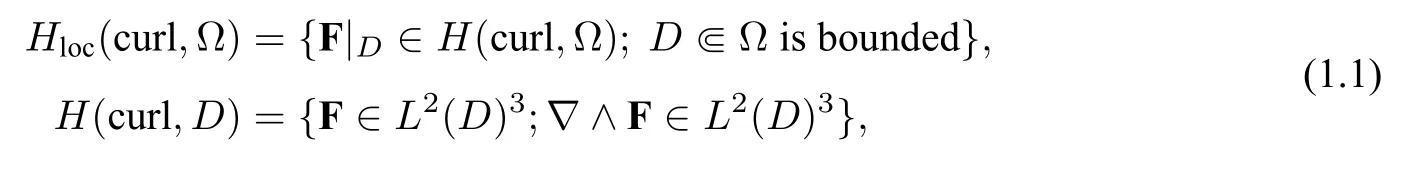
where Ω is an open set in R3.If a nontrivial pair of vector functions[E,H]∈Hloc(curl,Ω)×Hloc(curl,Ω)andk ∈R+solve the following equation

then [E,H] is referred to a pair of Maxwellian eigenfunction of (1.2) andkis the corresponding eigenvalue of (1.2).We emphasize that there is no homogeneous boundary condition for [E,H] on∂Ωin (1.2).Therefore,the spectral results in this paper can be applied to any conventional Maxwellian eigenfunctions with various boundary conditions which fulfill (1.2).In this paper,we shall study the local geometrical characterizations of [E,H] satisfying (1.2),where we assume that the corresponding Maxwellian eigenfunctions[E,H]satisfy certain homogeneous boundary condition on a cell of a plane in the interior of Ω.

Throughout this paper,we adopt the following notations.For a plane Π∈R3,any non-empty open connected subset Σ ⋐Π is referred to be acellof Π.Hence suppose that=ΠΣdenotes the connected component of Π∩Ω such that Σ ⋐Ω.LetBρ(x)be a ball centered atx∈R3with the radiusρ ∈R+.For a setK ⊂R3,Bρ(K) :={x;x∈Bρ(y)for anyy∈K}.In the following,we recall theedgeandvertexcorners in R3,which were introduced in[8,10,11].

Definition 1.1Let Π1and Π2be two adjacent planes of a polyhedronKwhich is contained in Ω.If the connected open portionl⋐Π1∩Π2such thatl⋐Ω,then any pointx0∈lis said to be an edge corner denoted byE(Π1,Π2,l);see Figure 1.

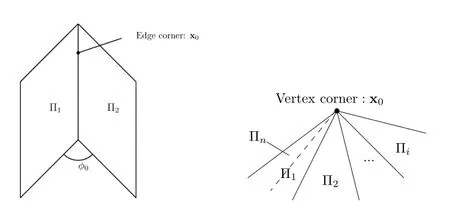
Figure 1 Schematic illustrations of the edge corner and vertex corner

Definition 1.2Let a polyhedral coneKwith the vertexx0∈Ω,wherebenplanes formingK.If there exits a sufficiently smallρ ∈R+such thatBρ(x0)∩K⋐Ω,thenK∩Bρ(x0)is called a vertex corner associated with Π1,Π2,...,Πn,and denoted by;see Fig.1.

In this paper,for a pair of Maxwellian eigenfunction[E,H]of(1.2),we only consider the geometrical structure ofEat a vertex corner pointx0whenEsatisfies certain kind of homogenous boundary conditions on the planes forming the vertex corner.Nevertheless,it is pointed out that the corresponding results can be equally extended toHin a similar manner.

Definition 1.3Suppose thatEis a Maxwellian eigenfunction of(1.2).Assume that Σ ⋐Ω is a cell of a plane Π.Σ is a perfect electromagnetic conductor cell ofEin Ω if the boundary conditionν ∧E|Σ=0is satisfied,whereνis one of the unit outward normal vectors to Σ.By analytic continuation,one has thatν ∧E|Π=0,and Π is said to be a perfect electromagnetic conductor plane(PEC plane)ofE.Similarly,ifν ∧(∇∧E)=0,Σ is called a perfect magnetic conductor plane(PMC plane).Letandsignify the sets of PEC planes and PMC planes ofEin(1.2),respectively.

In the following,we shall introduce the vanishing order of a Maxwellian eigenfunctionEto(1.2)at a given pointx0∈Ω.

Definition 1.4([21]) LetEbe a Maxwellian eigenfunction in(1.2)associated with the eigenvaluek ∈R+.For any fixed pointx0∈Ω,if one can find a numberN ∈N∪{0}such that

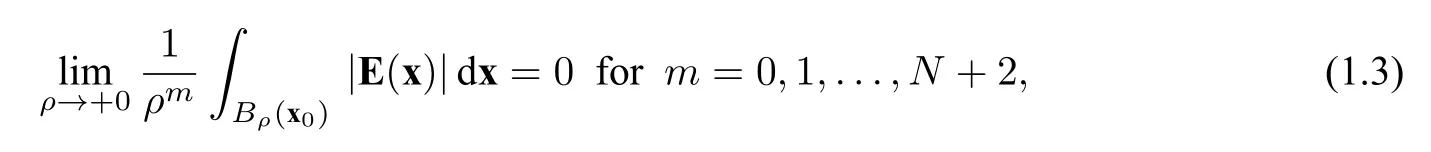
thenEis said to vanish atx0up to the orderN.The largest possibleNsuch that(1.3)is fulfilled is called the vanishing order ofEatx0,and we write

Definition 1.5LetEbe a Maxwellian eigenfunction to (1.2).Consider a vertex corner⋐Ω.If

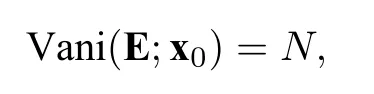
we say thatEvanishes atx0associated with the vertex corner up to orderN.

In this paper,we shall establish the vanishing order ofEassociated with a vertex corner⋐Ω as described above in the general scenario.

1.2 Physical background and connection to existing studies

In [21],the unique continuation property (UCP),namely the vanishing property,for Maxwellian eigenfunctions from an edge corner is considered.In this paper,we shall consider the UCP for Maxwellian eigenfunctions from a vertex corner.It is easy to see that a vertex corneris formed by finite many edge corners,where each edge corner is composed by any two adjacent planes.However,we shall not merely make use of the UCP results in[21],applying them to a vertex corner.Instead,we treat the vertex corner directly and derive some novel UCP results that are actually stronger than those in[21]in a certain sense.

It is pointed out that this type of UCP study is different from the conventional UCP studies in the literature,and it arises in the attack of a longstanding problem in the inverse scattering theory from a new perspective.The inverse problem aims to uniquely determine the shape of an impenetrable obstacle by minimal/optimal scattering measurements,and we refer interested readers to the survey papers [14,48]as well as some existing results [2,12,24,25,26,27,28,29,30,32,34,35,36,40,41,42,43,44,45,46,47,49,50] on this challenging topic.In [10,11],in tackling this inverse problem with generalized impedance-type obstacles within the polytope geometry associated with acoustic scattering,the authors show that the study can be reduced to analysing the UCP of the Laplacian eigenfunctions locally around a corner with certain homogeneous conditions imposed on the planes forming the corner.This program of study has been extended to the inverse electromagnetic and elastic scattering problems associated with the Maxwell and Lamé systems [8,18,19,21].Following the study in [21],one should also be able to establish certain new unique identifiability results for the inverse electromagnetic scattering problem by using the UCP results derived in this work,together with direct modifications of the related argument in[21],which we choose to skip in the present paper.Finally,we would like to mention in passing some related studies on the inverse problems of determining the shape of certain penetrable medium inclusions by minimal/optimal measurements[3,4,5,6,7,13,9,15,16,22,17,20,23,31,37,38,39]in different physical contexts.

The rest of the paper is organized as follows.In Section 2,we present some preliminary and auxiliary results.Sections 3 and 4 are devoted to the main UCP results.

2 Preliminary and auxiliary results

Since the Maxwellian operatorPdefined in(1.2)is invariant under rigid motions,in this paper we always suppose that the edge cornerE(Π1,Π2,l)⋐Ω fulfills

where 2His the length ofland Πℓ⋐Ω (ℓ=1,2) could be either one of the two types:a PEC or PMC plane.Therefore,one can identify thatllies on thex3-axis.Furthermore,let Π1coincide with the(x1,x3)-plane while Π2has a dihedral angleϕ0=απaway from Π1in the anti-clockwise direction.Please refer to Figure 2 for a schematic illustration.It is clear that one can suppose that

Figure 2 Schematic illustration of an edge corner formed by two intersecting planes with the dihedral angle ϕ0

When the vanishing order at an edge corner ofE(Π1,Π2,l) is investigated,we always suppose that that the underlying edge corner is the origin0∈l.Hence supposeνiis the unit normal vector corresponding to Πi,i=1,2.It can be directly to know thatνican be characterized by

In the subsequent content of this paper,we recall the spherical coordinate of any pointxin R3:

withx1=rsinθcosϕ,x2=rsinθsinϕandx3=rcosθ.It is well know that

is the orthonormal basis in the spherical coordinate system,where

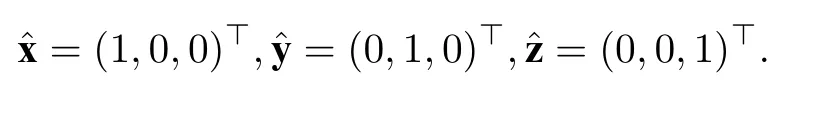
For a fixedl ∈N throughout of this paper we use the notation

Let the spherical harmonicsbe given by

whereis the associated Legendre functions.For simplicity,we use the notationfrom the clear context.Lemma 2.1 reviews the basic properties of the associated Legendre functions,which can be found in[1].

Lemma 2.1The following orthogonality condition of the associated Legendre functions holds

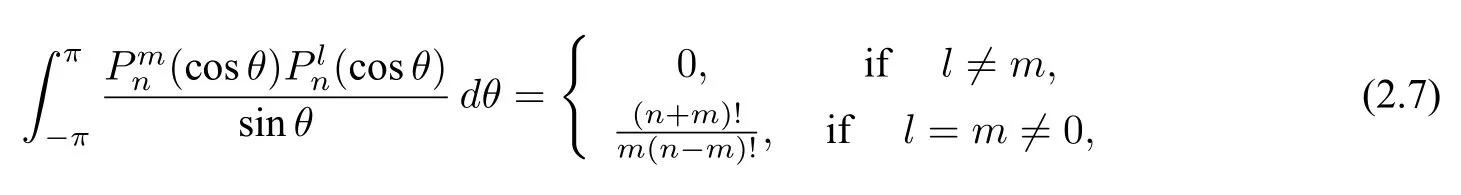
wheren ∈N is fixed,and any two nonnegative integersm ≤nandl ≤n.Also one has

wherel ∈N andm ∈[l]0.Ifis evaluated atθ=0,forl ∈N∪{0}we have

For a fixedn ∈N∪{0}andm ∈N withm ≤n,it holds that

Let the spherical Bessel functionjℓ(t)of the orderℓbe defined by

Furthermore,the following recursive relationships can be found in[1]:

From[21,Lemma 2.5],the radial wave expansion ofEis given by

where

The following lemmas are taken from[21].

Lemma 2.2([21],Lemma 2.8) LetEbe a Maxwellian eigenfunction to (1.2) associated with the eigenvaluek ∈R+.Recall thatEhas the radial wave expansion(2.13)at0.For a fixedN ∈N,if

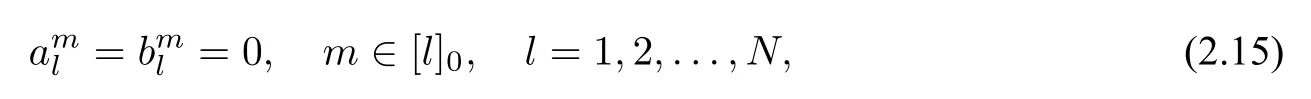
where[l]0is defined in(2.5),then

Conversely,if there exitsN ∈N such that(2.16)holds then we have(2.15).

Lemma 2.3([21],Lemma 2.9) LetEbe a Maxwellian eigenfunction to(1.2)associated with the eigenvaluek ∈R+.Consider an edge cornerE(Π1,Π2,l) ⋐Ω.Recall thatEhas the radial wave expansion(2.13)at0,andνidefined in(2.2)are the outward unit normal vectors to Πi.Then

3 Vanishing orders at a vertex corner intersected by PEC planes

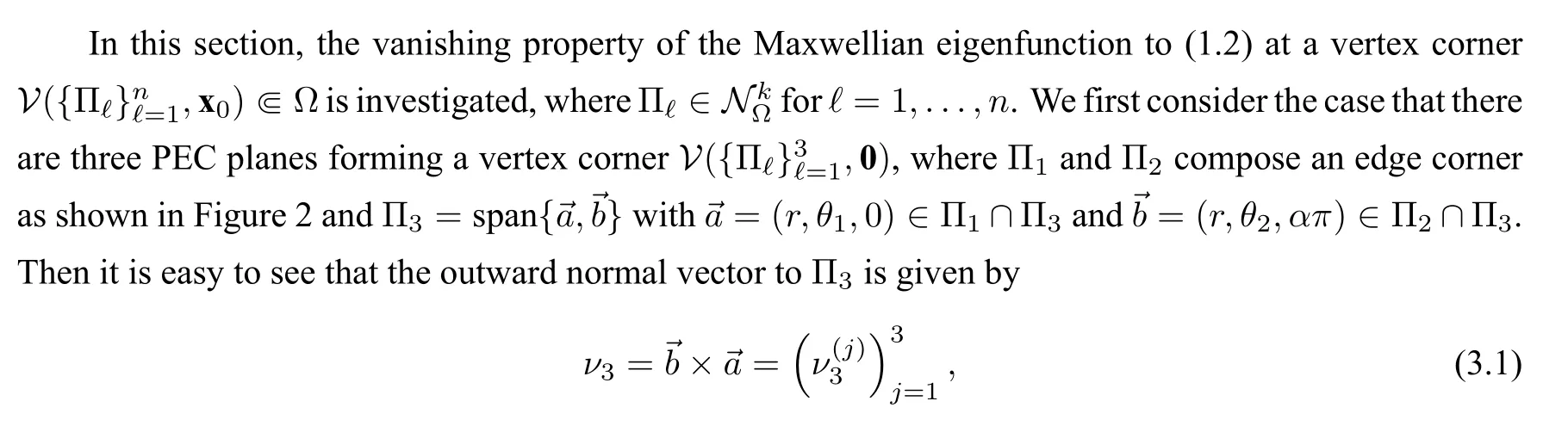
where

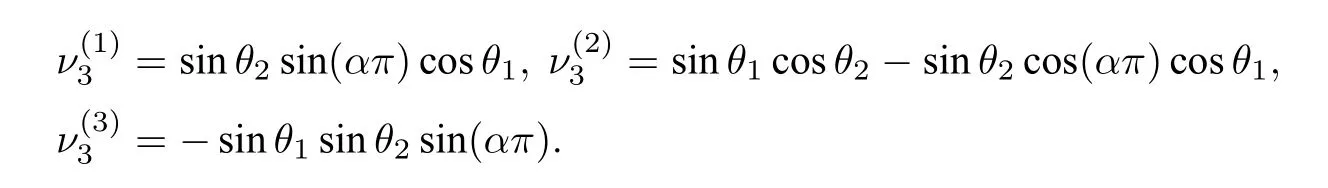
Please refer to Figure 3 for a schematic illustration.

Figure 3 Schematic illustration of a vertex corner intersected by Π1,Π2 and Π3

Figure 4 Schematic illustration of a vertex corner intersected by Π1,Π2,···,Πn where n>3

We are now in a position to study the general vanishing orders with the help of the radial wave expansion (2.13) of the Maxwellian eigenfunctionEto (1.2) around a vertex corner.Before that,we first need the following lemma,which can be found in[21,Lemma 4.1].

Lemma 3.1Suppose thatEis a Maxwellian eigenfunction to(1.2)associated with the eigenvaluek ∈R+.Let an edge cornerE(Π1,Π2,l) ⋐Ω where Πℓ ∈ℓ=1,2,∠(Π1,Π2)=ϕ0=απ,α ∈(0,1).It holds that

Assume that there exits an ∈N such that

then we have

and

Now we are in the position to give the main result for the vertex corner formed by three PEC planes.

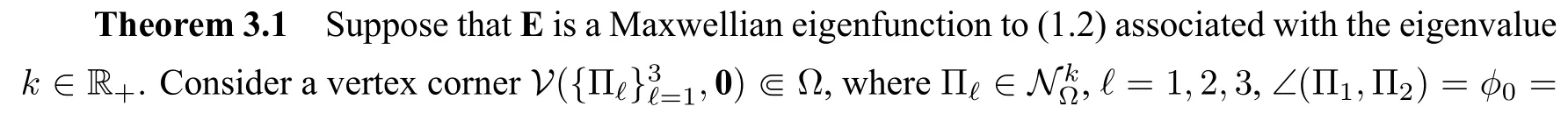
ProofWe prove this theorem by induction.Assume thatα1/2,we shall prove that Vani(E;0)≥1.From Lemma 3.1,we know that(3.2a),(3.2b)and(3.2c)hold.Therefore,using the fact thatα ∈(0,1),we have

In order to show that Vani(E;0)≥1 we only need to prove=0.Recall thatν3is defined in(3.1).It can be deduced that

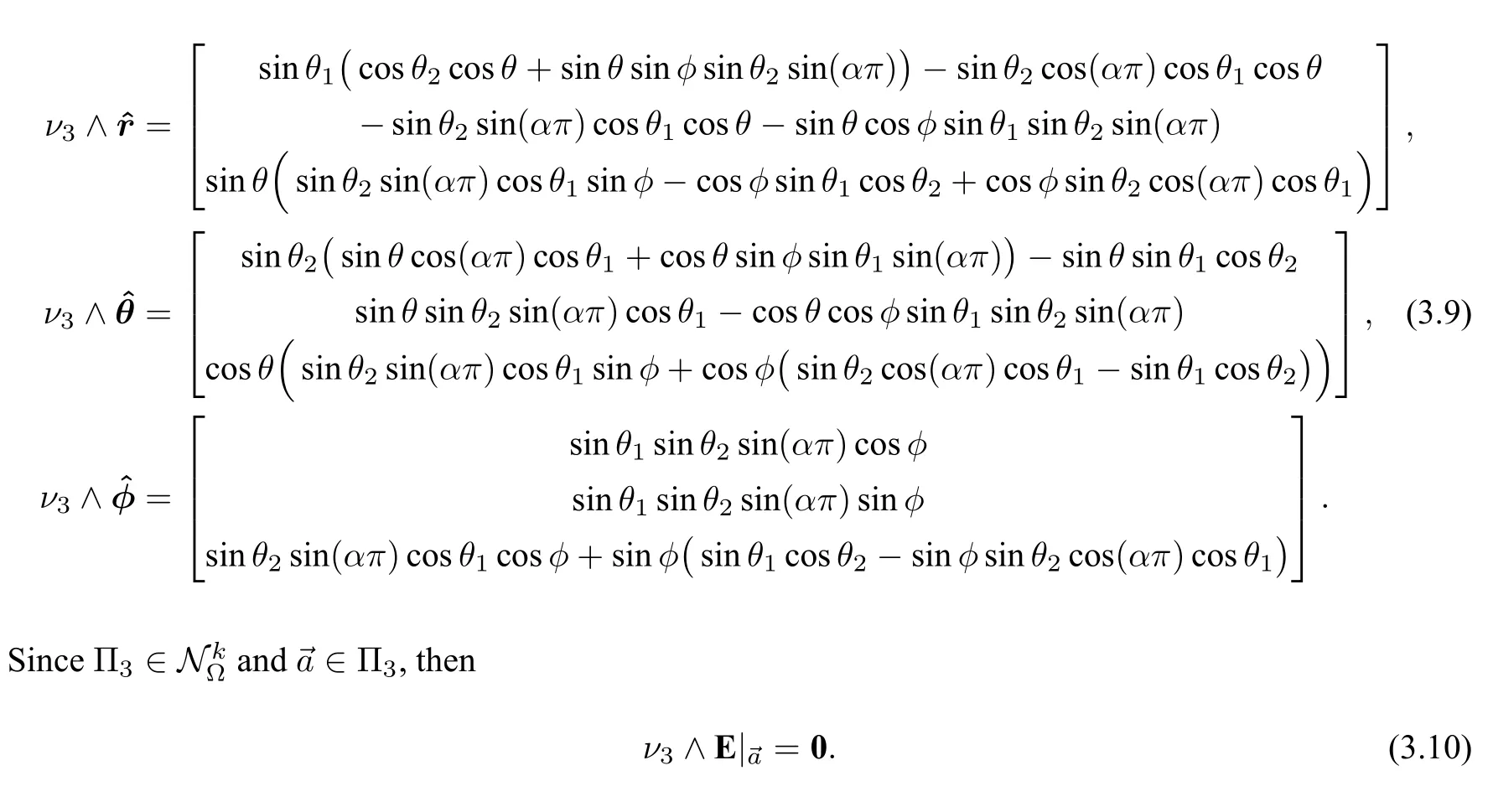
Substituting(3.9)into(3.10),we observe that the lowest order power ofrin(3.10)is 1.Comparing the coefficient ofr1on both sides of the first component of(3.10),we derive that

Under the assumptionα1,from Lemma 2.2,we have

By induction,we assume that

wheren ∈N,is the associated Legendre polynomial,and for a fixedp,q=1,2,...,p −1.Then by induction,we have

which implies that=0 and=0,wherel=1,2,···,n −1 andm ∈[l]0by virtue of Lemma 2.2.Hence from Lemma 3.1,we know that(3.4),(3.5)and(3.6)hold.Under the condition(3.13),it holds that form=1,...,nwe haveα,k=1,2,···,m −1,therefore

which can be used to derive that=0,m=1,...,nby using(3.4).Again using Lemma 3.1,we know(3.6)holds.Under the condition(3.13),from(3.6)we have

From Lemma 3.1,substituting(3.14)into(3.5),we obtain that

Utilizing the orthogonality property(2.7)together with(3.15),we can derive that

Under(3.13),it holds thatform=1,...,n,wherek=1,2,···,m −1,then

which can be used to derive that=0,∀m ∈[n]1.

The proof is complete.

ProofSince Π1and Π2are two PEC planes,from Lemma 3.1,we have

Therefore,it is easy to see that

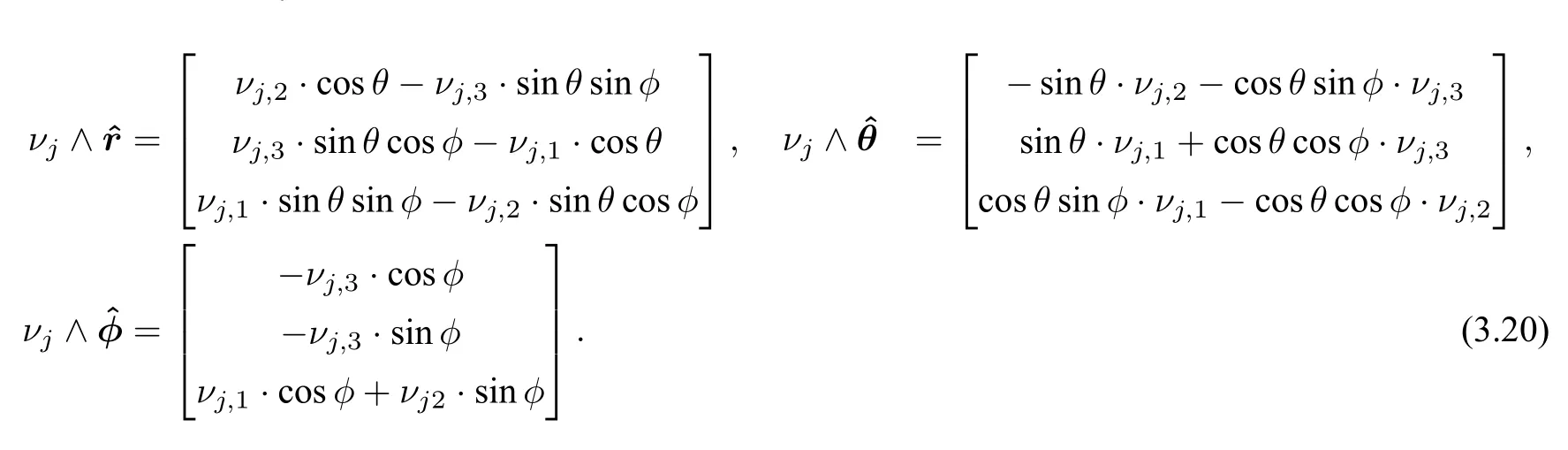
Substituting(3.20)into(3.19),we observe that the lowest order power ofrin(3.19)is 1.Comparing the coefficient ofr1on both sides of the first component of(3.19),we derive that

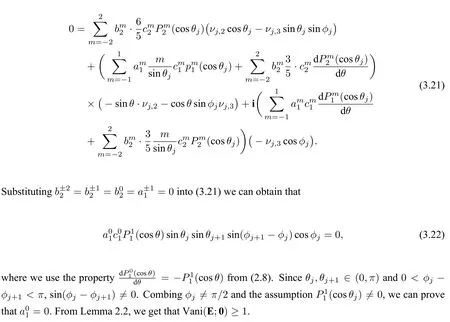
By induction,we assume that

wheren ∈N{1},is the associated Legendre polynomial,and for a fixedp,q=1,2,...,p −1.From the proof of Theorem 3.1,we know that

which can be further reduced to

The proof is complete.

4 Vanishing orders at a vertex corner intersected by PMC planes

Lemma 4.1LetEbe a Maxwellian eigenfunction to(1.2)associated with the eigenvaluek ∈R+.Suppose that there exits an edge cornerE(Π1,Π2,l)⋐Ω with Πℓ ∈ℓ=1,2,∠(Π1,Π2)=ϕ=απ,α ∈(0,1).It holds that

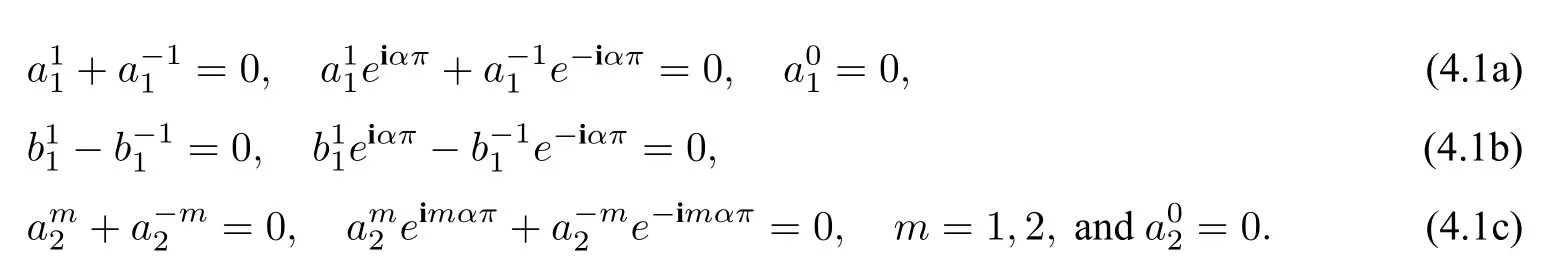
If one hasn ∈N such that

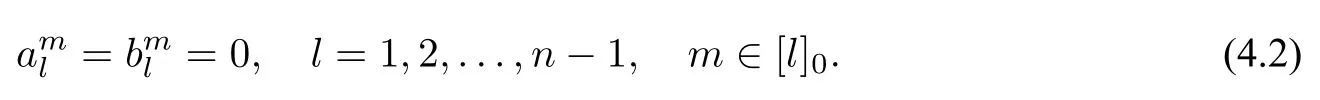
Then we have

We shall establish the vanishing order of a Maxwellian eigenfunction to(1.2)at a vertex corner formed by three PMC planes.

whereN ∈N,is the associated Legendre polynomial,andq=1,2,...,p −1 with a fixedp.

ProofWe prove this theorem by induction.Assume thatα1/2,we shall prove that Vani(E;0)≥1.From Lemma 4.1,we know that(4.1a),(4.1b)and(4.1c)hold.Therefore,using the fact thatα ∈(0,1),we have

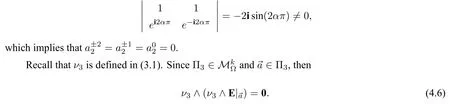
Substituting (3.9) into (4.6),we observe that the lowest order power ofrin (3.10) is 1.Comparing the coefficient ofr1on both sides of the first component of(4.6),we derive that

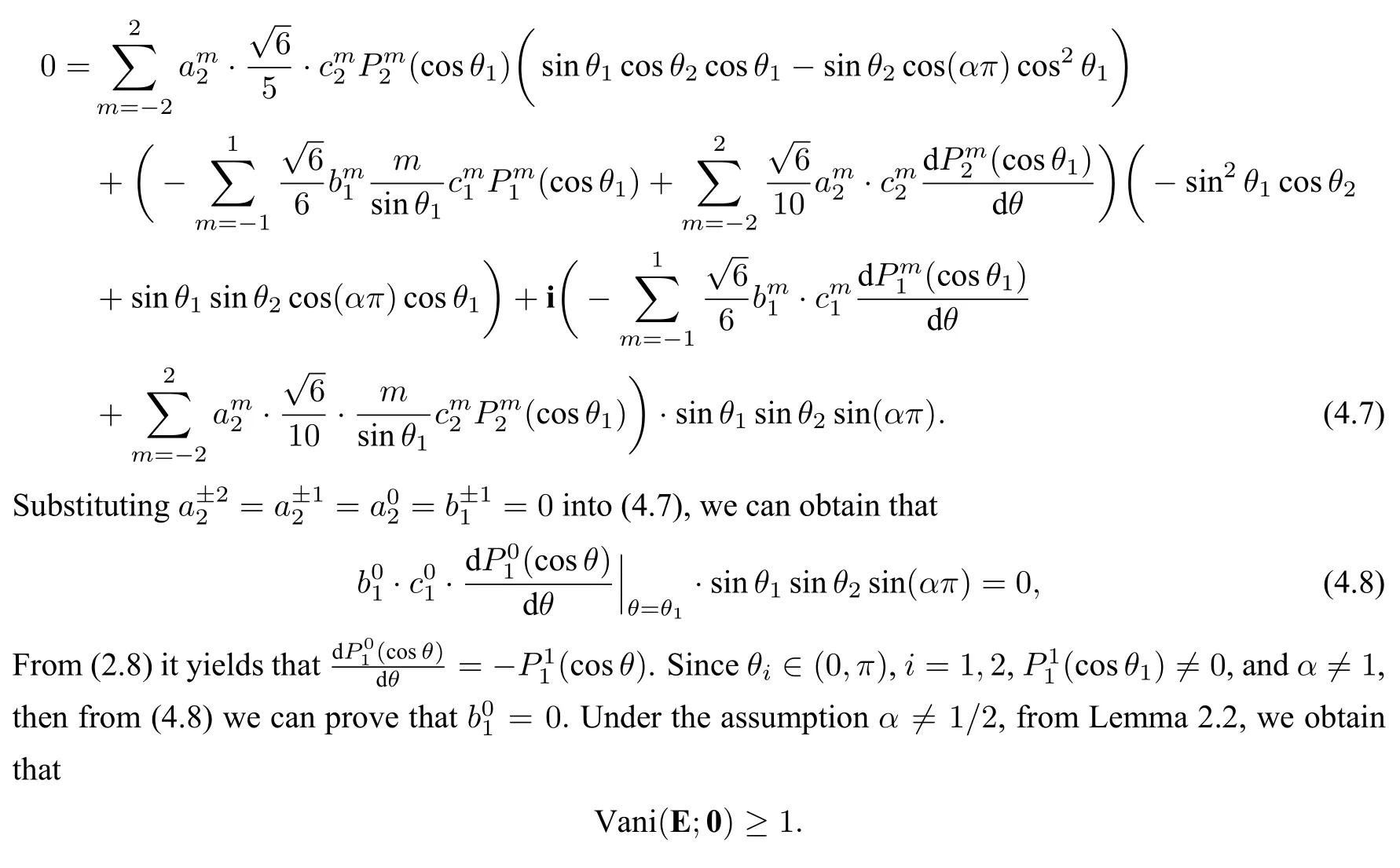
By induction,we assume that

wheren ∈N,is the associated Legendre polynomial,and for a fixedp,q=1,2,...,p −1.Then by induction,we have

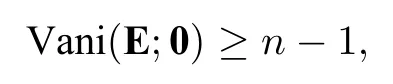
which implies that=0 and=0,wherel=1,2,···,n −1 andm ∈[l]0from Lemma 2.2.Hence from Lemma 3.1,we know that(4.3)holds.Under the condition(4.9),it holds that form=1,...,nwe haveα,k=1,2,···,m −1,therefore

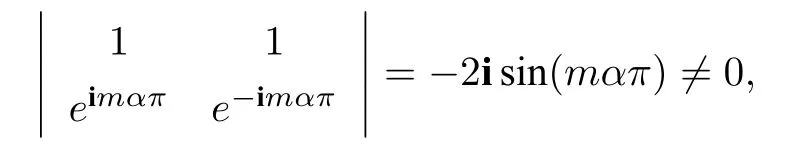
which imply that=0,m=1,...,nby using(4.3).Again using Lemma 3.1,we know(4.5)holds.Under the condition(4.9),from(4.5)we have

From Lemma 3.1,substituting(4.10)into(4.4),we obtain that

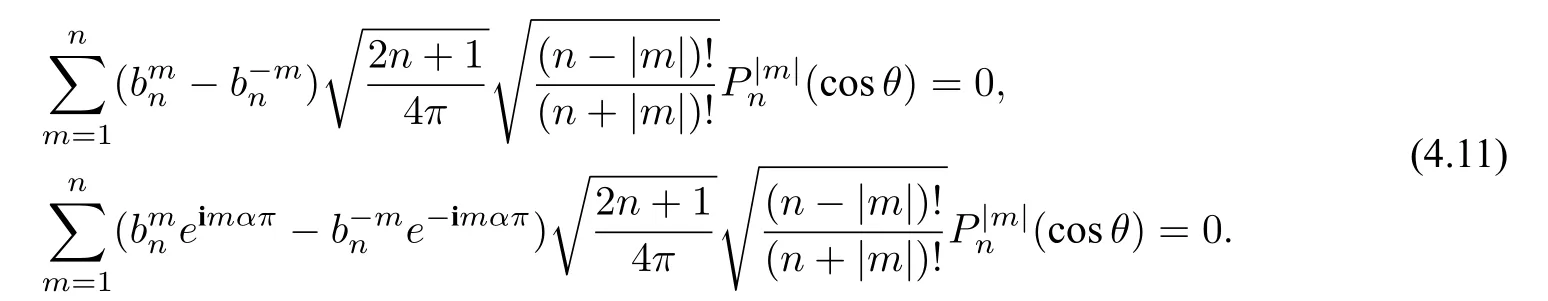
Utilizing the orthogonality property(2.7)together with(4.11),we can derive that

The proof is complete.

We can use the similar argument for proving Theorem 3.2 to investigate the vanishing order ofEat the vertex corner⋐Ω,wheren>3.We choose to skip the detailed proof of Theorem 4.2.

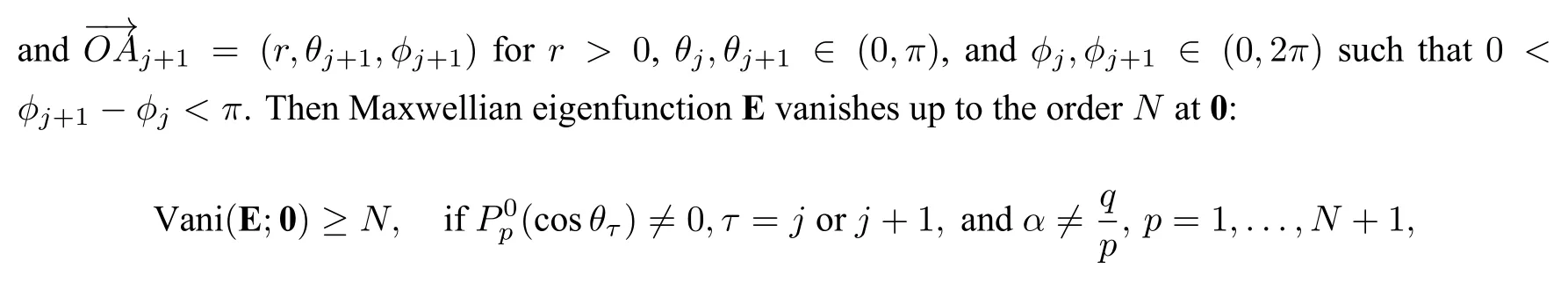
whereN ∈N,is the associated Legendre polynomial,andq=1,2,...,p −1 with a fixedp.