反双纽线三角函数的两个最佳不等式*
何晓红, 李少云
(1.衢州广播电视大学 教务处, 浙江 衢州 324000; 2.温州广播电视大学 教师教学发展中心, 浙江 温州 325000)
一、研究基础
反双纽线正弦和反双纽线双曲正弦函数[1]496-505 [2]259的定义分别为:
和

为论述方便,对这两个函数的极限值记为:[2]259
和
其中,
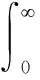
是经典伽马函数[3]1-17,并且
是第一类完全椭圆积分[4]1-10.对实数a,b,c∈且c≠0,-1,-2….将高斯超几何函数F(a,b;c;x)定义为:
其中,当a≠0时,(a,0)=1;当n∈≡{k:k是正整数}时,
是移位阶乘函数.
另一对反双纽线三角函数,即反双纽线正切函数和反双纽线双曲正切函数分别定义为[5]77-94:

和
近几年,反双纽线三角函数的性质和不等式引起了国内外许多研究者的关注,并取得了丰硕成果.例如:陈超平建立了反双纽线三角函数的Wilker和Huygens型不等式[6]673-684
对所有0<|x|<1成立.
还有学者给出了反双纽线三角函数之间的不等式[7]1-14
arctl(x) 对所有x∈(0,1)成立. 本文的主要目的是发现并证明最佳参数α1,α2,β1,β2∈(0,1),使得双向不等式 α1arcsl(x)+(1-α1)arcslh(x) α2arctlh(x)+(1-α2)arctl(x) 对所有x∈(0,1)成立. 为证明本文的主要结果,需要一些反双纽线三角函数的基本知识和三个引理. 我们记下面两个反双纽线函数值为: 根据反双纽线三角函数的定义和求导法则,我们容易得到它们的导数公式: 引理1设x1,x2∈且x1 在区间(x1,x2)内也是(严格)递增(递减)的[8]10. 引理2函数 φ(x)=(1+x4)3/2+(1-x4)3/2-2 证明:对函数φ(x)求导,可得 (1) 对所有x∈(0,1)成立.注意到: (2) 所以,引理2容易从式(1)和式(2)得到. 引理3函数 φ(x)=(1+x4)7/4+(1-x4)7/4-2 证明:对函数φ(x)求导,可得 (3) 对所有x∈(0,1)成立.注意到: (4) 所以,引理3容易从式(3)和式(4)得到. 下面给出本文的主要结果并证明之. 定理1双向不等式 α1arcsl(x)+(1-α1)arcslh(x) (5) 对所有x∈(0,1)成立,当且仅当α1≤(1-σ)/(ω-σ)=0.190 0L和β1≥1/2. 证明:不等式(5)可以写成: (6) 简单计算可得: (7) (8) 其中,φ(x)定义在引理2. (9) 定理2双向不等式 α2arctlh(x)+(1-α2)arctl(x) (10) 对所有x∈(0,1)成立,当且仅当α2≤(1-τ)/(κ-τ)=0.108 9L和β2≥1/2. 证明:不等式(10)可写成: (11) 简单计算可得: (12) (13) 其中,φ(x)定义在引理3. (14) 根据定理1和2,我们可得到如下最优不等式: 定理3双向不等式 对所有0<|x|<1成立. 自17世纪末以来,反双纽线三角函数得到了深入的研究,许多国内外数学工作者取得了丰硕的研究成果.本文通过对四个反双纽线三角函数的比较,推得了反双纽线正弦函数和反双纽线双曲正弦函数,以及反双纽线正切函数和反双纽线双曲正切函数凸组合的两个精确不等式,这对进一步研究反双纽线三角函数之间的关系具有重要的理论意义.二、三个引理

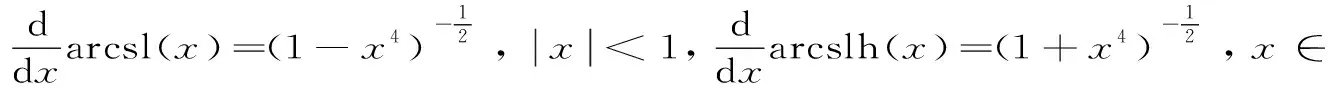


三、主要结果
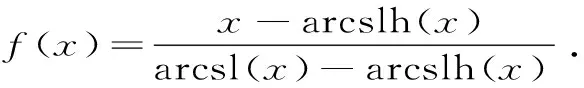



四、结 语

