一个积分平均的调和、正弦和双曲正切平均确界*
杨 萍 萍
(湖州市体育运动学校 理科教研组, 浙江 湖州 313000)
一、研究背景
设r∈(0,1),第一类和第二类完全椭圆积分κ(r)和ε(r)分别定义为:
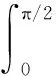
且满足:
κ(0+)=ε(0+)=π/2,κ(1-)=+∞,ε(1-1)=1,
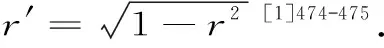
函数κ(r)和ε(r)可表示为:
其中,Gauss超几何函数定义为:
且当a≠0时,(a)0=1;当n∈≡{k:k是正整数}时,(a)n=a(a+1)(a+2)…(a+n-1)=Γ(a+n)/Γ(a)为移位阶乘函数,Γ(x)=e-ttx-1dt(x>0)是经典Gamma函数.
近年来,第二类完全椭圆积分ε(r)的确界引起了国内外许多数学学者的关注,得到了许多特殊情形的关于ε(r)的重要不等式.例如:有人证明了λ=3/2和μ=log2/log(π/2)=1.534 9L,是使得双向不等式
对所有r∈(0,1)成立的最佳参数[2]693-699[3]289-312.
Wallis比定义为[4]1-11 [5]303-307:

且满足:
(1)
第二类完全椭圆积分ε(r)应用Wallis比Wn可以写成:
(2)
设x,y>0且x≠y,则调和平均H(x,y),几何平均G(x,y),算术平均A(x,y),正弦平均Msin(x,y),双曲正切平均Mtanh(x,y)和涉及第二类完全椭圆积分ε(r)的积分平均V(x,y)分别定义为[6]1 071-1 092:
(3)
(4)
(5)
(6)
且不等式
H(x,y) (7) 和 A(x,y) (8) 对所有x,y>0且x≠y成立. Anderson,Vuorinen等证明了函数r→ε(r)/(1-r2)在区间(0,1)内是严格单调上升的且值域为(π/2,∞).由等式(6)可得 H(x,y) (9) 对所有x,y>0且x≠y成立[1]54. 由不等式(7)~(9)可得 H(x,y) (10) 对所有x,y>0且x≠y成立. 根据不等式(10),本文将证明存在最佳参数α1,α2,β1,β2∈,使得双向不等式 和 对所有x,y>0且x≠y成立. 为证明本文主要结果,需要以下引理: 引理1对-∞ 也在(a,b)内单调上升(下降);如果f′(x)/g′(x)的单调性是严格的,则结论中的单调性也是严格的[1]10. 引理3函数 在区间(0,1)内是严格单调上升的,且值域为(π/4,∞)[1]70. 引理4函数 在区间(0,1)内是严格单调上升的,且值域为(3/14,1-2/π). 证明:设f1(r)=1-2ε(r)/π,f2(r)=1-r′2sin(r)/r.简单计算可得: (10) (11) 其中, 设φ1(r)=r2sin(r)-rr′2cos(r)+sin(r),φ2(r)=r3,φ3(r)=(2+r′2)sin(r)+4rcos(r)和φ4(r)=3r.简单计算可得 (12) (13) (14) (15) 对所有r∈(0,1)成立. (16) 引理5函数 在区间(0,1)内严格单调上升且值域为(3/16,1-2/π). 证明:函数g(r)可写成: g(r)=cosh(r)γ(r), (17) 其中, 根据式(1),式(2)和幂级数展开式有: (18) (19) 设 (20) 由等式(18)~(20),使得 (21) (22) 对所有n≥0成立. 由不等式(22)和引理2可以清楚地看到函数γ(r)在区间(0,1)内是单调上升的,这样等式(17)和函数cosh(r)协同γ(r)的单调性导致的结论是,函数g(r)在区间(0,1)内是严格单调上升的.注意到: (23) 所以,引理5容易从等式(23)和函数g(r)的单调性得到. 定理1双向不等式 对所有x,y>0且x≠y当且仅当α1≤2/π,β1≥11/14时成立. 证明:根据H(x,y),Msin(x,y)和V(x,y)是对称的且一阶齐次.不失一般性,我们假设x>y>0.设r=(x-y)/(x+y)∈(0,1).则由等式(3),(4)和(6),使得 (24) 其中,f(r)定义在引理4. 所以,定理1容易从引理4和等式(24)得到. 定理2双向不等式 对所有x,y>0且x≠y当且仅当α2≤2/π和β2≥13/16时成立. 证明:根据H(x,y),Msinh(x,y)和V(x,y)是对称的且一阶齐次.不失一般性,假设x>y>0.设r=(x-y)/(x+y)∈(0,1).则由等式(3),(5)和(6),使得 (25) 其中,g(r)定义在引理5. 所以,定理2容易由引理5和等式(25)得到. 根据定理1和定理2,可得到第二类完全椭圆积分ε(r)的一个新的上下确界: 推论3双向不等式 综上,平均值理论是一个既经典又十分活跃的数学分支,现已渗透到应用数学的许多领域.本研究利用调和平均、正弦平均和双曲正切平均,对一个积分平均进行估计,获得了两个最佳不等式,并由此发现了第二类完全椭圆积分的精确上下界。所得结果大大改进了已有的相关不等式.本研究方法对从事特殊函数理论研究的爱好者具有一定的借鉴作用.二、引 理
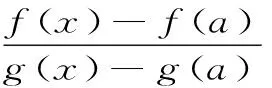

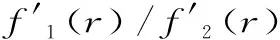
三、主要结果


