Toader型平均的两个最佳不等式*
张 帆
(湖州职业技术学院 建筑工程学院, 浙江 湖州 313000)
一、研究背景
设0 第一类和第二类完全椭圆积分满足下列微分公式和Landen恒等式[1]474-475: 且第一类完全椭圆积分κ(r)在区间(0,1)内严格单调递增,第二类完全椭圆积分ε(r)在区间(0,1)内严格单调递减. 设x,y>0和x≠y.则将调和平均H(x,y),几何平均G(x,y),算术平均A(x,y),Toader平均T(x,y)[2]358-368,正弦平均Msin(x,y)和双曲正切平均Mtanh(x,y)[3]1 071-1 092分别定义如下: (1) (2) (3) 最近,Toader平均,正弦平均和双曲正切平均与其他二元经典平均的比较得到了国内外学者的深入研究,在特殊情形下,发现了许多关于完全椭圆积分,三角函数和双曲函数的重要不等式. 有人证明了λ=3/2和μ=ln2/ln(π/2)=1.534 9L是使得双向不等式 Mλ(x,y) 还有人证明了双向不等式 A(x,y) (4) 对所有x,y>0和x≠y成立[3]1 078. 显然,双向不等式 H(x,y) (5) 对所有x,y>0和x≠y成立. 从不等式(4)和(5)可推得 H(x,y) (6) 对所有x,y>0和x≠y成立. 根据不等式(6),本文的主要结果为以下两个定理: 定理1双向不等式 对所有x,y>0和x≠y成立的充分必要条件是:α1≤4sin2(1)/π2=0.286 9L和β1≥9/14. 定理2双向不等式 对所有x,y>0和x≠y成立的充分必要条件是:α2≤4tanh2(1)/π2=0.235 0L和β2≥9/16. 为证明本文的主要结果,需要以下引理: 引理1对-∞ 也在(a,b)内单调上升(下降);如果f′(x)/g′(x)的单调性是严格的,则结论中的单调性也是严格的[3]10. 引理3幂级数公式: 其中,Bn是Bernoulli数[7]4 874-4 888. 引理4双向不等式 对所有n∈+成立,其中Bn是Bernoulli数[8]1-14. 引理5(1)函数r[κ(r)-ε(r)]/r2在区间(0,1)内是严格单调递增的,且值域为(π/4,1)[1]70.(2)函数r[ε2(r)-r′2κ2(r)]/r4在区间(0,1)内是严格单调递增的,且值域为(π2/32,1)[1]70. 引理6函数rε(r)[(1+r2)ε(r)-r′2κ(r)]/r2在区间(0,1)内是严格单调递减的,且值域为(2,3π2/8). 证明:设 φ(r)=ε(r)[(1+r2)ε(r)-r′2κ(r)]/r2. 简单计算可得: (7) (8) 所以,引理6容易从引理5及等式(7)和(8)得到. 引理7函数 在区间(0,1)内严格单调递增,且值域为(7/3,2/sin2(1)). 证明:简单计算可得: (9) (10) 其中, λ1(r)=3rsec2(r)-r3sec2(r)-3tan(r)+r2tan(r)-2r3. 由引理3得到: (11) 其中, (12) 由引理4和等式(12)得到: (13) 其中, ϖ1(n)=12n(22n+2-1)(22n-1-1)-π2(n-1)(22n-1)(22n+1-1)> 22n[22n+1((12-π2)n+π2)-3((18-π2)n+π2)]+(12-π2)n+π2> 22n[22n+1((12-π2)n+π2)-3((18-π2)n+π2)]+2n+π2. (14) 应用二项式展开式,可得: 22n+1((12-π2)n+π2)-3((18-π2)n+π2)> 2(1+2n)((12-π2)n+π2)-3((18-π2)n+π2)= 4(12-π2)n2+5(π2-6)-π2>132-7π2>0, (15) 且对所有n≥2成立. 所以,引理7容易从等式(9)~(11)和不等式(13)~(15)得到. 引理8函数 在区间(0,1)内是严格单调递增的,且值域为(8/3,2coth2(1)). 证明:函数μ(r)可变为: (16) 由双曲正弦函数和双曲余弦函数的幂级数展开公式可得: r2sinh(3r)+sinh(3r)+r2sinh(r)+sinh(r)+4r3cosh(r)-4rcosh(r)= (17) (18) 设 (19) 则由等式(16)~(18)得到: (20) (21) 其中, ω(n)=32n+1[(4n+7)32n+4-2(192n3+536n2+356n+9)]-(48n2+148n+111). (22) 应用二项式展开式可得: (4n+7)32n+4-2(192n3+536n2+356n+9)> 2 208n3+3 464n2-388n+549>0. (23) 由等式(22)和不等式(23)得: ω(n)>32n+1(2 208n3+3 464n2-388n+549)-(48n2+148n+111)>3(2 208n3+3 464n2-388n+549)-(48n2+148n+111)=6 240n3+9 320n2-1 876n+1 629>0, (24) 且对所有n∈成立. 根据引理2和等式(19)~(21)协同不等式(24)导致的结论是:函数μ(r)在区间(0,1)内严格单调递增.注意到, (25) 所以,引理8容易从等式(25)和函数μ(r)的单调性得到. 定理1的证明:根据二元平均H(x,y),Msin(x,y)和T[A(x,y),G(x,y)]是对称的且一阶齐次,不失一般性,假设x>y>0,r=(x-y)/(x+y)∈(0,1).则由等式(1)和(2)得到: (26) 设f1(r)=4ε2(r)/(π2r′4)-1和f2(r)=r2/[r′4sin2(r)]-1.简单计算得到: f1(0+)=f2(0)=0,f(r)=f1(r)/f2(r), (27) (28) 其中,函数λ(r)定义在引理7. (29) 定理2的证明:根据二元平均H(x,y),Mtanh(x,y)和T[A(x,y),G(x,y)]是对称的且一阶齐次,不失一般性,假设x>y>0,r=(x-y)/(x+y)∈(0,1).则从等式(1)得到: (30) 设f1(r)=4ε2(r)/(π2r′4)-1和f3(r)=r2/[r′4tanh2(r)]-1.则简单计算得到: f1(0+)=f3(0)=0,g(r)=f1(r)/f3(r), (31) (32) 其中,函数μ(r)定义在引理8. (33) 根据定理1和定理2,得到推论如下: 推论1双向不等式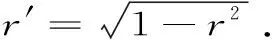



二、引 理


三、主要结果的证明