钢桁腹混凝土组合梁试验与承载力设计方法研究
蒋明利 陈建兵 匡冠桦
苏州科技大学土木工程学院,江苏苏州215000
钢桁腹混凝土组合梁(图1)是由混凝土顶板、混凝土底板、钢桁腹杆组成的受力体系。其特点是用钢桁腹杆代替传统的混凝土腹板,同时省去了上、下弦杆,解决了传统混凝土箱梁腹板容易开裂的问题,并减轻了箱梁的自重;不连续的腹杆使得箱梁的通透性较好,提高了桥梁的抗风能力;钢桁腹杆可工厂化预制,施工方便[1]。作为新兴的钢-混组合结构,钢桁腹混凝土组合梁以其高效的传力机制和良好的经济效益,已被应用于国内的桥梁建设中[2]。

图1 钢桁腹混凝土组合梁
国内学者针对钢桁腹混凝土组合梁的受力性能进行了相关的试验和理论分析。杭子豪等[3]基于欧拉-伯努利理论,分析了钢桁腹混凝土组合梁的受弯性能,提出了弯曲荷载作用下钢桁腹混凝土组合梁任意点的挠度公式及腹杆的轴力公式;朱虎勇等[4]通过对变截面钢桁腹混凝土组合梁的变形试验,提出了变截面组合梁弹性阶段的刚度简化计算方法;王彤等[5]利用箱梁理论对钢桁腹混凝土组合梁的空间受力性能进行分析,提出了桁腹式组合梁桥的弯曲、扭转、畸变的计算公式;董峰等[6]通过对我国第一座钢桁腹预应力混凝土组合梁桥进行动静载试验,对该桥的实际应力、挠度、自振频率等进行了理论分析。
目前,对于等截面钢桁腹混凝土组合梁未见试验研究。本文采用试验研究与理论分析相结合的方法,对钢桁腹混凝土组合梁的受力性能及承载力计算方法进行研究。
1 试验概况
1.1 试验模型
为避免单个试验带来的偶然性,设计制作了两片相同的试验梁。试验梁总长度为3 600 mm,计算跨径为3 360 mm,节点间距为420 mm,斜腹杆与混凝土板的水平夹角均为60°,斜腹杆与直腹杆的夹角为30°,混凝土顶板宽1 000 mm,板厚80 mm,混凝土底板宽550 mm,厚80 mm。试件截面尺寸见图2。

图2 试件截面尺寸(单位:mm)
钢桁腹杆采用Q345B级钢管,腹杆规格均为50 mm×5 mm,腹杆节点采用焊接连接,焊接前对钢管进行角度切割。顶底板采用强度等级为C45 的商品混凝土,混凝土顶底板采用双层配筋,顶板的箍筋、顶板的两层纵向钢筋以及底板的箍筋均采用直径为8 mm 的HRB400 钢筋,底板的两层纵向钢筋采用直径分别为12、16 mm 的HRB400 钢筋。钢桁腹杆节点处开有直径12 mm 的孔,孔内贯穿横向钢筋来提高节点的抗剪能力。节点构造见图3。
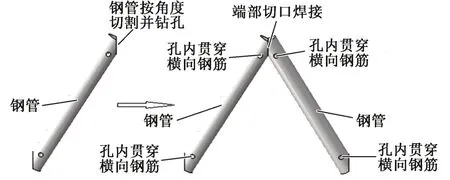
图3 节点构造
1.2 材料性能
在浇筑试验梁的同时制作了截面尺寸为150 mm×150 mm × 150 mm 的标准立方体试件,与试验梁同条件养护。采用标准试验方法测得混凝土立方体的平均抗压强度为54.46 MPa。
钢桁腹杆按照GB/T 2975—2018《钢及钢产品力学性能取样位置及试样制备》要求从母材中切取,并根据GB T228.1—2010《金属材料拉伸试验(第1 部分:室温试验方法)》的规定进行试样拉伸。按照同样的方法测得钢筋的屈服强度和抗拉强度。试验结果见表1。

表1 钢材材性试验结果
1.3 试验内容及加载方案
通过DH3821 型静态应变测试系统对试验梁各个截面的竖向挠度、纵向应变、各腹杆轴向应变等进行测量,包括L/2 截面、L/4 截面、3L/8 截面、L/2 截面(L为计算跨径)。对试验梁的腹杆进行编号,在腹杆的中部沿轴向每隔90°布置1个应变片,在对称侧腹杆布置1个应变片,以检查试验过程中是否发生偏载。同时,为了避免支座沉降的影响,在两个支座轴心线上布置两个位移计测量支座沉降量。测点布置见图4。

图4 测点布置
试验梁的加载装置见图5。通过调整试验梁下方的支座螺栓,将试验梁设置为简支梁的约束形式。采用跨中双点对称加载方案,两加载点在跨中形成840 mm 纯弯段。正式加载之前先对试验梁进行预加载,以消除试验梁与加载装置的间隙影响,同时检查各测量仪器是否正常工作,持荷2 ~3 min,然后卸载。正式加载采用分级加载的方式,每级荷载为20 kN,加载至160 kN 时荷载增量改为10 kN,直至试验梁破坏为止。为保证试验结果的可靠性,两片试验梁加载方案相同。

图5 试验梁加载装置
2 试验结果与分析
2.1 试验现象
试验梁在加载的过程中,破坏形态表现为典型的弯曲破坏,并未出现节点破坏及钢桁腹杆和混凝土板之间的剪切破坏。加载初期,因为施加荷载值较小,通过贯穿钢筋连接在一起的混凝土顶底板与钢桁腹杆协同工作、共同受力,试验梁表现出良好的弹性工作状态;随着荷载不断增加,混凝土顶板与分配梁支座接触部分可听到混凝土被挤压的声音,钢桁腹杆出现张拉绷紧的声音;当加载至200 kN 时,在混凝土底板加载点斜下方靠近跨中的节点处,观察到一细小裂缝;当加载至290 kN 时,在底板混凝土与钢桁腹杆的节点处,底板的侧面开始出现大小不一的裂缝,跨中位置裂缝较为明显;当加载至310 kN 时,跨中底板开始出现长裂缝;随着荷载不断增加,裂缝逐渐增大,加载至410 kN 时,混凝土底板在加载点的正下方处出现横向贯穿裂缝,顶板混凝土与分配梁接触部分起皮,表明试验梁已破坏,试验加载结束。
两片试验梁的加载现象大致相同(图6),试验梁2在荷载加至210 kN 时,跨中节点处开始出现第1 条微小裂缝,极限承载力和试验梁1基本相同,但在相同荷载下试验梁1 的裂缝数量比试验梁2 多,这是钢桁腹和混凝土板的制作质量引起的。

图6 试验梁弯曲变形及破坏特征
2.2 荷载-挠度曲线
钢桁腹混凝土组合梁跨中荷载-挠度曲线见图7。可知,钢桁腹混凝土组合梁在加载过程中经历了弹性、塑性和破坏3 个阶段。当荷载P<300 kN 时,跨中挠度随荷载增加呈线性发展的趋势,表明该阶段钢桁腹混凝土组合梁的整体工作性能良好;当300 kN<P<410 kN 时,钢桁腹混凝土组合梁整体刚度降低,达到塑性状态,其挠度的增长速率增大,荷载增长速率减小;当P>410 kN 时,钢桁腹混凝土组合梁的刚度明显降低,荷载-挠度曲线呈下降趋势,此时承载力不再增加,挠度却不断增大,表明钢桁腹混凝土组合梁进入破坏状态。总体上钢桁腹混凝土组合梁具有良好的延性和变形性能。

图7 荷载-挠度曲线
2.3 竖向挠度
试验梁1、试验梁2 的试验结果基本一致,对试验梁2进行数据分析。钢桁腹混凝土组合梁实测挠度沿梁跨径的变化曲线见图8。可知,各测点挠度随荷载增大而增加,在弹性阶段变化曲线比较均匀;当钢桁腹混凝土组合梁底板钢筋进入屈服状态后,各测点挠度沿梁跨的变化曲线仍保持一致,但挠度增量比弹性阶段明显增大。

图8 钢桁腹混凝土组合梁实测挠度沿跨径的变化曲线
2.4 跨中截面的纵向应变
钢桁腹混凝土组合梁跨中截面的实测纵向应变沿截面高度的分布情况见图9。可知:钢桁腹混凝土组合梁在加载过程中,混凝土顶板主要承受压应力,底板主要承受拉应力;纵向应变沿梁高近似呈线性分布,截面应变分布基本符合平截面假定。

图9 钢桁腹混凝土组合梁跨中截面纵向应变
2.5 腹杆轴向应变
钢桁腹混凝土组合梁腹杆的平均荷载-应变曲线见图10。由于结构为对称结构,以左半跨为参考。可知,随着荷载的不断增加,钢桁腹杆的轴向应变在不断增大,其中腹杆 1#、3#、5#、7#、9#杆为压杆,腹杆 2#、4#、6#、8#杆为拉杆,同一节点的腹杆之间存在拉压交替的现象。

图10 钢桁腹混凝土组合梁腹杆平均荷载-应变曲线
3 有限元分析
3.1 有限元模型
利用有限元软件ABAQUS 建立与试验梁相同的有限元分析模型(图11),模型中混凝土顶底板均采用实体单元C3D8R 模拟,钢桁腹杆采用S4R 壳单元模拟,钢筋采用T3D2桁架单元模拟。

图11 有限元模型
3.2 有限元模拟结果与分析
钢桁腹混凝土组合梁有限元分析结果见图12。可知:①钢桁腹混凝土组合梁的整体变形性能良好;②顶底板混凝土裂缝出现的位置与试验现象基本一致;③钢桁腹混凝土组合梁承受竖向荷载时,腹杆主要承受轴力作用,荷载首先由混凝土板传递给钢桁腹杆,腹杆再以拉压交替的方式将荷载传递到支座;④腹杆节点处出现应力集中的现象,应力主要集中在焊接部位和穿孔部位。

图12 有限元分析结果
4 极限承载力设计方法
4.1 钢桁腹混凝土组合梁的破坏形式
钢桁腹混凝土组合梁的极限承载力与破坏形式有关。根据剪跨比、荷载形式以及构造的不同,其破坏形式(图13)主要分为两类:剪切破坏和弯曲破坏,也可称之为局部失效破坏和整体失效破坏。当混凝土底板的受拉钢筋和顶板混凝土未达到屈服强度,而钢桁腹混凝土组合梁的腹杆或节点先发生破坏称为剪切破坏。发生剪切破坏时,受拉钢筋与混凝土并未充分发挥作用,钢桁腹混凝土组合梁整体变形较小,属于脆性破坏。该种破坏形式下钢桁腹混凝土组合梁的承载力主要由节点刚度和腹杆承载力控制,极限承载力较小。当混凝土底板的受拉钢筋和顶板混凝土达到屈服强度时发生的破坏称为弯曲破坏。发生弯曲破坏时材料被充分利用,混凝土顶板被压碎,腹杆与底板的变形明显,属于延性破坏。该种破坏形式下钢桁腹混凝土组合梁的承载力主要由抗弯刚度控制[7]。

图13 钢桁腹混凝土组合梁的破坏形式
4.2 剪切破坏形式下的承载力计算
腹杆或节点的破坏均与腹杆的轴力有关,当两者之一发生时,即可认为钢桁腹混凝土组合梁达到了极限状态[8]。钢桁腹混凝土组合梁承受竖向荷载时,弯矩主要由顶底板混凝土承担,而剪力主要通过钢桁腹杆承担。取任意钢桁腹杆节点,通过内力平衡条件求钢桁腹杆轴力。钢桁腹杆轴力计算如图14所示。

图14 钢桁腹杆轴力计算示意
考虑节点D的平衡得到DB杆的轴力NDB为

式中:Q1为第 1 根腹杆DB受到的剪力;φ为钢桁腹杆的竖向夹角。
考虑节点B的平衡得到BF杆的轴力NBF为

式中:Q2为第2根腹杆BF受到的剪力。
由2.5 节可知,钢桁腹混凝土组合梁同一节点的两根腹杆受力规律表现为一压一拉交替,以受拉为正,受压为负,则第i腹杆的轴力Ni为

式中:Qi为第i根腹杆受到的剪力。
保证拉(压)杆不因强度不足而破坏的条件为
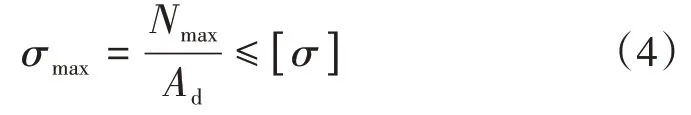
式中:σmax为腹杆应力最大值;Nmax为腹杆轴力最大值;Ad为腹杆的截面面积;[σ]为材料的容许应力。
若保证钢桁腹混凝土组合梁不发生屈曲破坏,应满足

式中:Ncr为屈曲破坏的临界荷载;Ed为腹杆的弹性模量;Id为腹杆的惯性矩;ld为腹杆的长度。
钢桁腹杆的轴力差使得节点承受很大的竖向剪力,其抗剪承载力Vu计算式为

式中:Vc为混凝土的抗剪承载力;Vsv为贯穿钢筋的抗剪承载力。
根据GB 50010—2010《混凝土结构设计规范》,节点区混凝土提供的抗剪承载力Vc为

式中:ft为混凝土抗拉强度设计值;b,h0分别为节点截面的有效宽度和有效高度。
根据GB 50017—2014《钢结构设计规范》,单根贯穿钢筋受剪面提供的抗剪承载力Vsv为

式中:nv为受剪面数目;d为贯穿钢筋直径;fv为贯穿钢筋的抗剪强度设计值。
4.3 弯曲破坏形式下的承载力计算
计算钢桁腹混凝土组合梁弯曲破坏形式下的承载力时作如下假定:①弹性范围内,钢桁腹混凝土组合梁顶板、底板在竖向荷载作用下满足平截面假定;②忽略混凝土的抗拉能力对钢桁腹混凝土组合梁整体抗弯承载力的影响;③忽略钢桁腹杆的纵向弯曲刚度,即不考虑钢桁腹杆的抗弯能力;④位于塑性中性轴以上的混凝土应力达到抗压强度,取矩形应力图计算,混凝土底板钢筋达到屈服强度,应力分布为矩形[9-12]。
计算钢桁腹混凝土组合梁极限抗弯承载力时,根据中性轴位置的不同,将钢桁腹混凝土组合梁分为两种类型截面,见图15。图中:beff为混凝土板的有效宽度;hu为混凝土顶板的厚度;h为梁高;h0为截面有效高度;fcd为混凝土抗压强度设计值;As为底板受拉钢筋的截面面积;fsd为底板抗拉钢筋强度设计值;x为混凝土顶板顶面至中性轴之间的距离。

图15 钢桁腹混凝土组合梁抗弯承载力计算图示
第Ⅰ类截面中x≤hu,钢桁腹混凝土组合梁截面的中性轴位于混凝土顶板内,判断条件为

钢桁腹混凝土组合梁中性轴的位置为

由受压区混凝土合力作用点力矩之和为0的平衡条件可得钢桁腹混凝土组合梁极限抗弯承载力Mu为
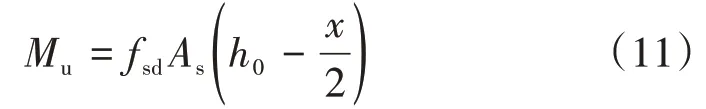
由受拉区钢筋合力作用点力矩之和为0的平衡条件可得

第Ⅱ类截面中x≥hu,钢桁腹混凝土组合梁截面的中性轴位于混凝土顶板外,判断条件为

对于第Ⅱ类截面,尽管截面的中性轴位于钢桁腹杆,但在不考虑钢桁腹杆抗弯的情况下,其极限抗弯承载力仍可参考式(11)求得,或由受拉区钢筋合力作用点力矩之和为0的平衡条件求得

由于钢桁腹杆在横截面垂直方向并不连续,忽略了钢桁腹杆的抗压能力,所以式(14)在计算极限承载力时偏于保守,因此,推荐使用式(11)计算极限抗弯承载力。
4.4 计算结果对比
根据试验测试结果,主梁的破坏是由于跨中截面底板受拉钢筋屈服,使梁丧失承载力,从而使结构达到极限承载力,判断其破坏形式为弯曲破坏。由式(10)计算出钢桁腹混凝土组合梁中性轴的位置,判断其为第I 类截面的梁,再由式(11)或式(12)求得钢桁腹混凝土组合梁的极限抗弯承载力。
钢桁腹混凝土组合梁极限抗弯承载力计算结果对比见表2。可知,试验值、有限元计算值及理论值相差较小,试验梁1、试验梁2、有限元计算值与理论值的比值分别为1.11、1.08、1.05,有限元计算值与理论值更为接近,且试验值与有限元计算值均大于理论值,说明本文提出的承载力计算方法安全可靠。

表2 极限抗弯承载力计算结果对比 kN·m
5 结论
1)钢桁腹杆与混凝土顶底板协同工作,整体性能良好且具有较好的延性。
2)钢桁腹混凝土组合梁在试验过程中未出现腹杆屈曲破坏及节点的剪切破坏,表现出良好的剪切屈曲稳定性。
3)在平截面假定的基础上,提出了钢桁腹混凝土组合梁的承载力计算方法,并通过与试验值、有限元计算值对比,验证了公式的准确性。

