飞机机电作动器模糊PI-ANN复合控制仿真

鹿山山,王志胜,欧阳权,段朝伟,丛玉华,2,肖志慧,赵祥丹

(1.南京航空航天大学 自动化学院，南京 211106;2.南京理工大学紫金学院 计算机学院，南京 210023)

1 引言

随着功率电传技术和机电技术的发展，越来越多的机载设备采用电能取代传统飞机上的液压能、气压能和机械能，多电/全电飞机开始大量出现[1，2]。飞机的机电作动器类似于人体的肌肉组织，是飞机控制系统的执行机构，通过带动舵面实现飞行姿态控制，常称为“舵机”[3]。与传统的液压作动器相比，机电作动器降低了作动系统的复杂性，增加了安全性与可靠性，减小了维修难度，提高了能量转换效率[4-5]。飞机要求机电作动器的环境适应能力强、性能稳定、快速性好、强抗干扰能力等，电机是机电作动器的核心执行部件[6]，其中应用最为广泛的是永磁同步电机(permanent magnet synchronous motor，PMSM)，具有高可靠性、大功率密度、小体积、低成本等优点[7]。

电机控制系统是机电作动器的关键组成部分。文献[7]提出了一种适用于永磁同步电机的位置跟踪控制器，由非线性扩张状态观测器、轨迹微分器和动态表面控制组成，通过仿真验证了位置跟踪器,提高了位置跟踪精度、抗干扰能力与抑制混沌性能；文献[8]设计了含有速度调节和电流调节的永磁同步电机双闭环回路，通过仿真和试验表明控制系统有较好的静态、动态性能；文献[9]用模糊PI控制器代替速度环中的传统PI控制器，通过仿真实验证明了电动车的永磁同步电机加速时间缩短、电机输出转矩脉动减小；文献[10]提出了基于气隙磁场定向的永磁同步电机矢量控制策略，通过仿真证明了设计策略能有效降低谐波对磁链的干扰；文献[11]将模糊原理加入到位置环传统PID中，通过仿真证明了其有更好的适应性，但对系统内部的非线性因素和外部干扰没有进行分析和补偿。

传统PI控制容易实现，因而在实际工程中依旧应用广泛[12]，然而机电作动器具有非线性、多变量、强耦合的特点，传统PI控制效果达不到性能要求[13]。智能控制中的模糊控制与神经网络控制都有着广泛的应用[14]。针对机电作动器作动精度与抗扰动的问题，基于传统三闭环控制，利用模糊控制调节简单、应用性强的优点[15]，将模糊理论加入到位置环，设计模糊PI控制，在不同状态下调节PI参数以提升系统的性能；将自适应神经网络引入到速度环，通过神经网络逼近非线性干扰函数，提高系统的抗干扰能力[16]。

2 飞机机电作动器数学模型

飞机机电作动器可以分成电机部分与机械传动部分，模型如图1所示[5]。

2.1 电机部分

对常用的表贴式三相PMSM数学模型进行研究[17]，在d-q坐标系下，建立电机定子磁链方程组为：

(1)

式(1)中：ψd和ψq分别是定子磁链的直轴和交轴分量；Ld和Lq分别是定子电感的直轴和交轴分量，Ld=Lq=L；id和iq分别是电流直轴和交轴分量；ψr是转子磁链。在d-q坐标系下，电机定子电压方程组与电磁转矩为：

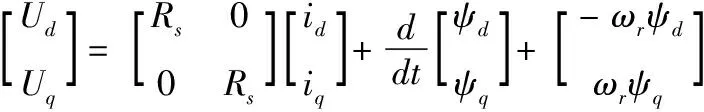
(2)

Te=np(ψdiq-ψqid)

(3)

式(2)～(3)中：Ud和Uq分别表示定子电压的直轴和交轴分量；Rs是电机定子电阻；ωr=npωm是电机电气角速度，np是电机极对数，ωm是电机机械角速度；Te为电机的电磁转矩[18]。

2.2 机械传动部分

机械传动部分如图2所示[19]。

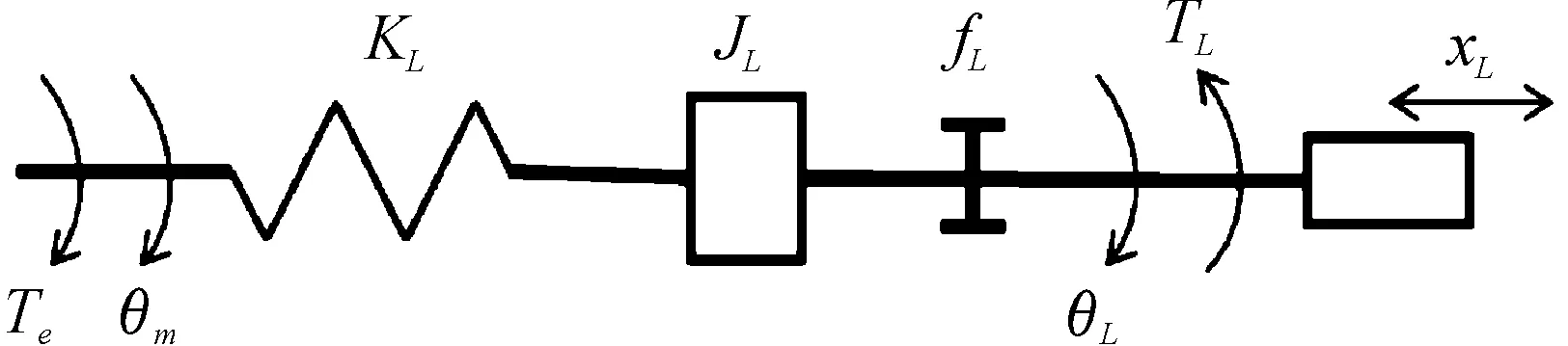
图2 机械传动部分示意图

图2中，Te是电机输出电磁转矩，θm是电机输出角度，KL是作动部分等效扭转刚度，JL是等效转动惯量，fL是阻力等效阻尼系数，θL是丝杠旋转角度，TL是作动点等效负载转矩，xL是作动位移，xL=kθL/2π，k为滚珠螺母系数。建立的运动方程与转矩方程分别为：

(4)

Te(t)=KL[θm(t)-θL(t)]

(5)

对上式进行拉普拉斯变换，可以得到：

(6)

综合式(1)～式(4)，选择xL、θL、ωm、iq和id作为状态变量，机电作动器的状态空间模型可以写成：

(7)

式(7)中：A、B、C、E为系数矩阵；x是状态变量；u是控制输入；v为干扰量；y表示系统输出。具体表达如下：

3 模糊PI-ANN控制

机电作动器是高阶非线性强耦合系统，在位置环中基于传统PI控制引入模糊理论，提高控制系统的环境适应能力，但不能抑制干扰力矩；由状态空间模型可知，干扰力矩对角速度存在直接影响，所以设计时在速度环中引入神经网络控制以补偿干扰力矩的影响。

3.1 模糊PI控制设计

PID控制中微分的引入会放大噪声导致系统性能下降，所以本文只引入了PI控制，PI的控制律可以写为：

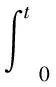
(8)

传统PI控制的参数不能根据工作状态做出实时调整，因此位置环中在传统PI控制上加入模糊控制，提高系统的精确度和快速性等[20]。单变量二维模糊PI控制器示意图如图3。

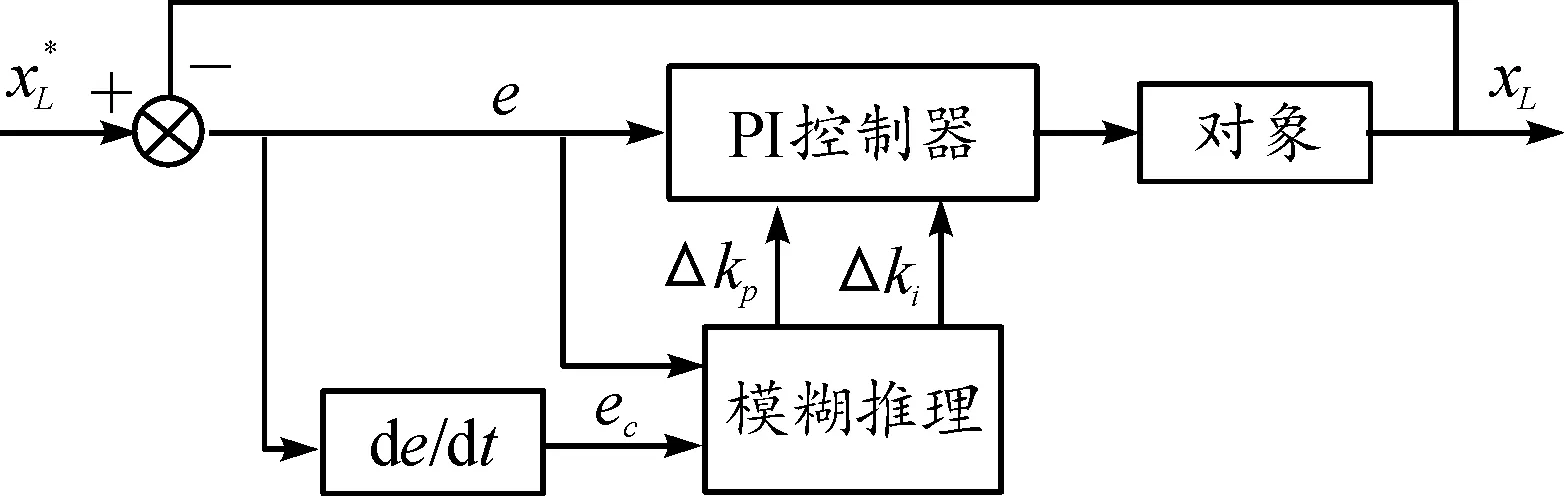
图3 位置环模糊PI控制器示意图

(9)

式(9)中：kp和ki是模糊PI控制器调节后参数，kp0和ki0是PI控制器初始参数。

模糊推理的输入量是误差e和误差变化量ec，分别定义在模糊论域E，EC上，输出量是Δkp和Δki，分别定义在模糊论域KP，KI上，e、ec、Δkp和Δki的模糊集均为{负大(NB)，负小(NS)，零(ZO)，正小(PS)，正大(PB)}，均服从三角隶属度函数，模糊推理选用max-min方法和面积重心法去模糊化。

根据e和ec的变化，kp和ki整定原则如下：

1)当|e|较大时，Δkp取正大，Δki取负大，使系统有较好的跟踪性能；

2)当|e|较小时，Δkp取正小，Δki取负小，避免系统出现较大的超调；

3)当|e|非常小、|ec|较大时，说明系统还没有稳定，Δkp取正小，Δki取正大，使系统快速达到稳态；

4)当|e|非常小、|ec|较小时，说明系统即将达到稳态，Δkp取零，Δki取正小；

5)当|e|、|ec|都非常小时，说明系统达到稳态，Δkp和Δki都取零，控制器参数保持不变。

根据以上的整定规则，得到Δkp和Δki的模糊规则如表1所示。

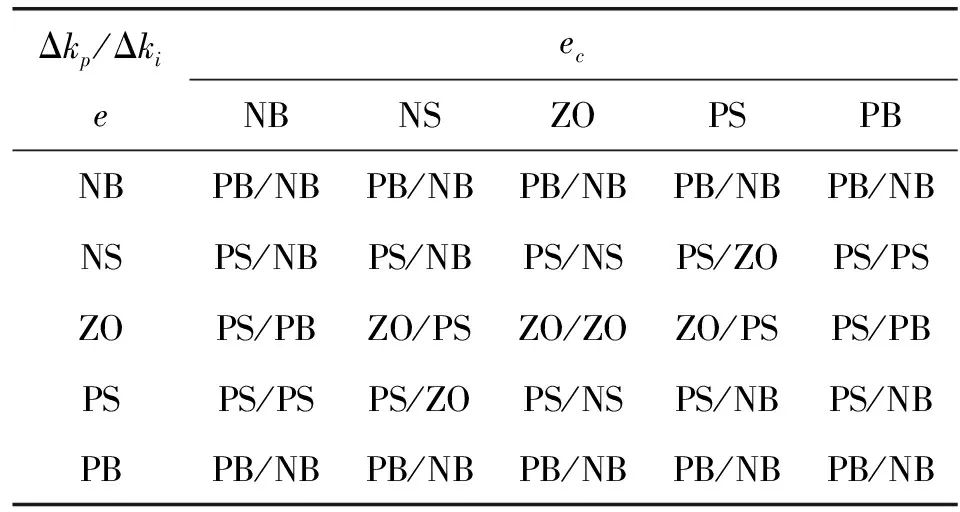
表1 Δkp和Δki模糊规则表

由式(6)可知，电机输出角度信号超前于作动点位移信号，为改善动态加速过程，在位置环的反馈中，用电机输出角度与作动点位移共同反馈，位置环反馈表达式为：

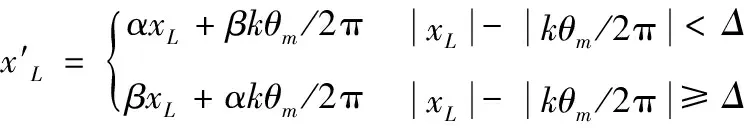
(10)

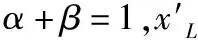
3.2 自适应神经网络设计

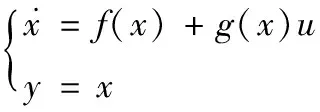
(11)

式(11)中：x=ωm是状态变量，f(x)是未知非线性函数；g(x)是已知函数；u∈R和y∈R分别为速度环子系统的控制输入和输出。定义速度误差信号为：

(12)

(13)

将式(13)代入式(11)，可得到误差系统为：

对上式拉式变换变成(s+Kp)E(s)=0，对应的根是s=-Kp，只要系数Kp大于0就能保证速度环子系统的稳定性。但是控制律中存在不确定非线性函数f(x)，无法直接实现控制。

神经网络优越的逼近能力已经在许多文献中得到证明[21-22]，设计RBF神经网络逼近未知函数f(x)。自适应神经网络框图如图4。

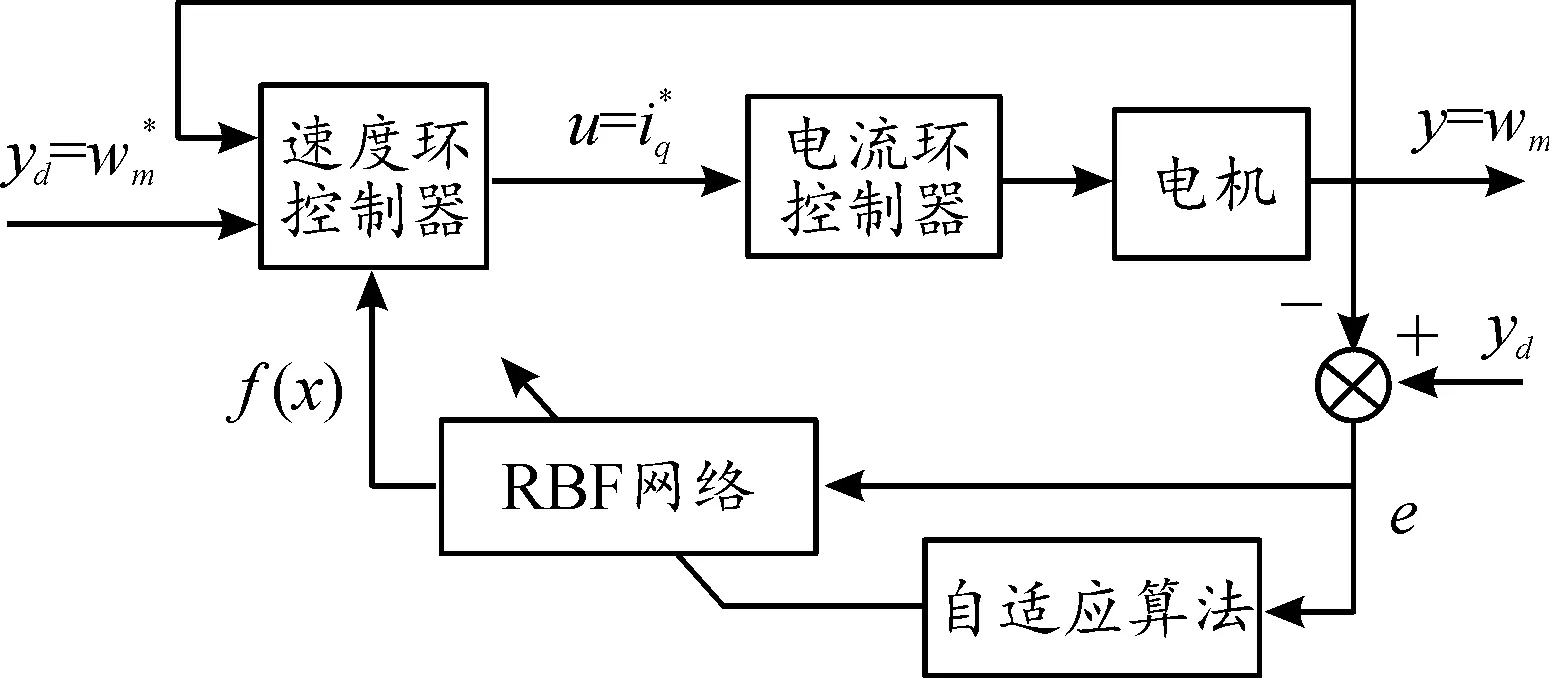
图4 速度环自适应神经网络框图

(14)

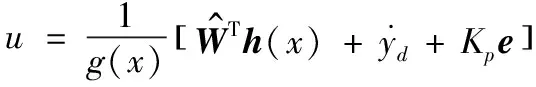
(15)

利用Lyapunov方法求出RBF神经网络权重调节的自适应律为[23]：

(16)

式(16)中：γ和p是2个可调正常数；e为速度误差信号；b在系统里是常数1。

通过构建合适的Lyapunov函数，可以证明本文设计的自适应神经网络是稳定的[23]。设计合适的Kp、p满足-eTKppe≤0和选取逼近误差非常小的神经网络，根据LaSalle不变性原理，则速度环闭环系统是渐进稳定的，且系统的收敛速度取决于Kp和p的值。

4 仿真结果

4.1 模糊PI控制仿真

在Matlab/Simulink构建机电作动器仿真模型，如图5所示，表2是机电作动器的物理参数。

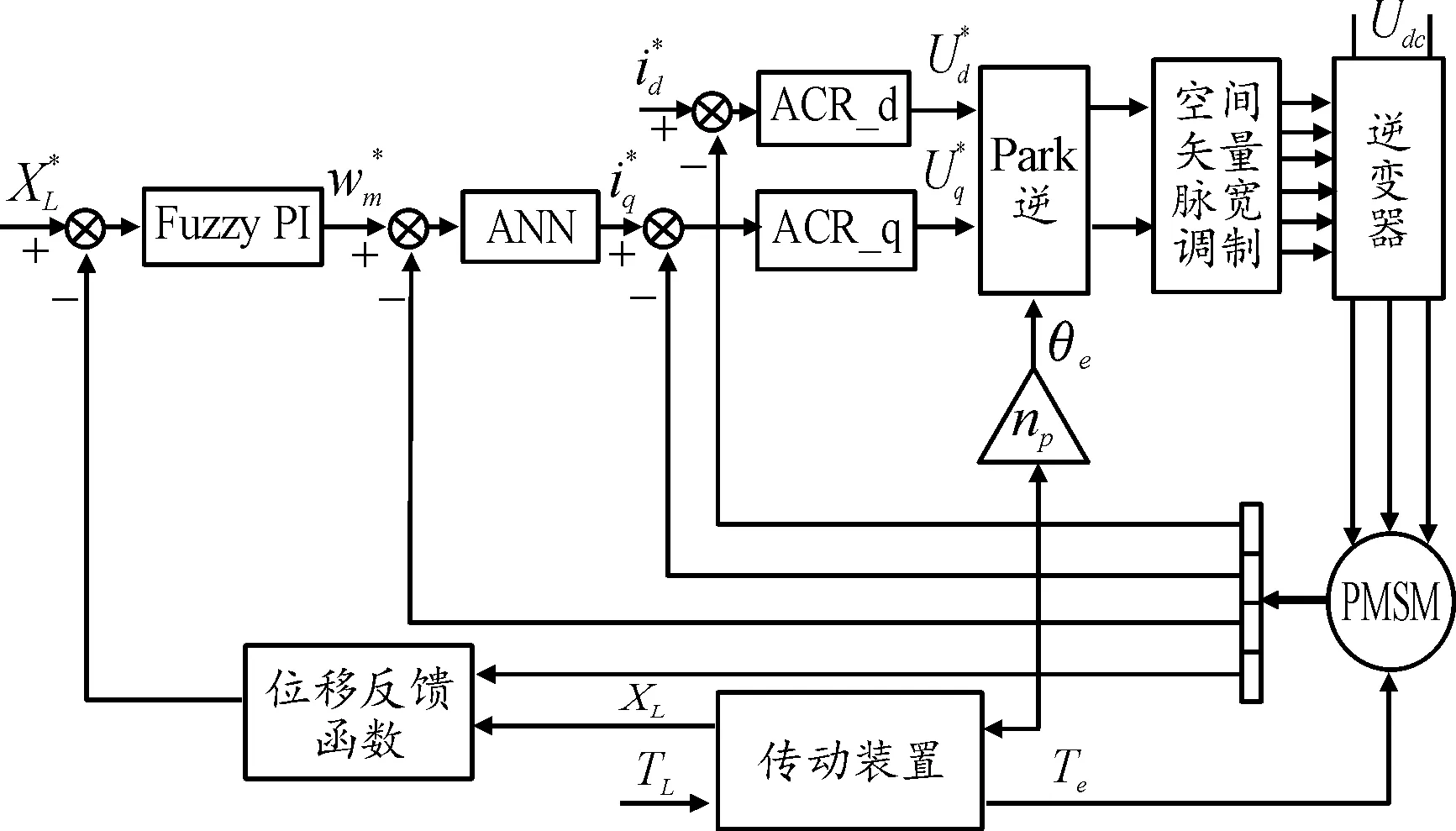
图5 机电作动器仿真模型示意图

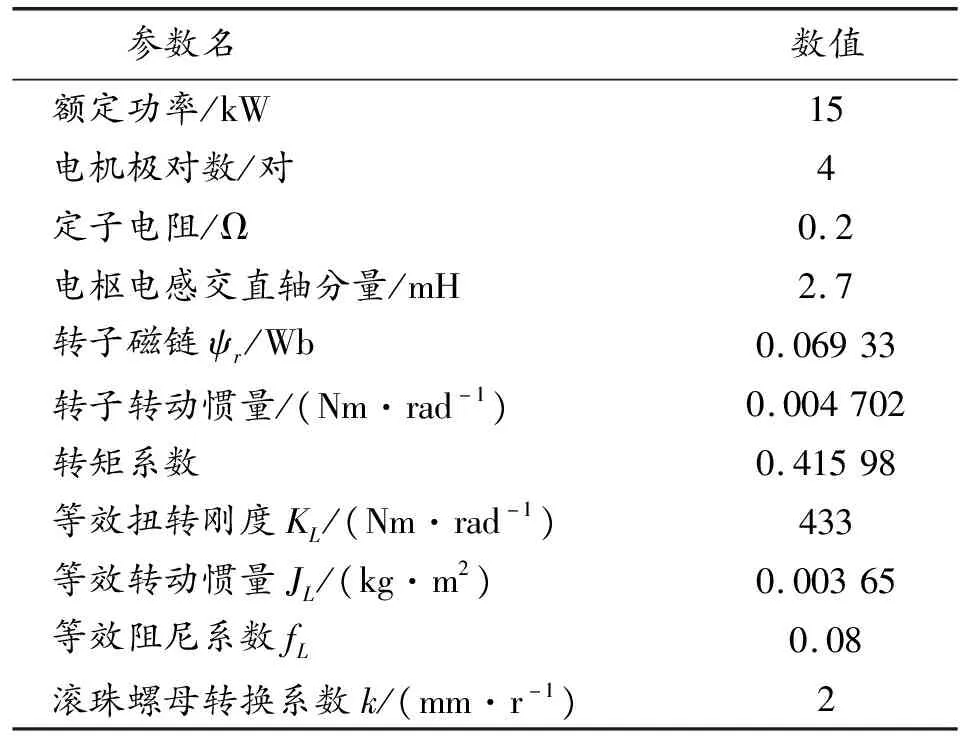
表2 机电作动器参数

机电作动器传统三闭环PI控制器的控制参数为位置环(P=60，I=6)、速度环(P=6.5，I=2)、电流环(P=10，I=3)。

模糊PI控制器中，e、ec、Δkp和Δki的模糊论域定义在E=[-1.5,1.5]、EC=[-20,20]、KP=[-40,40]、KI=[-6,6]，由Δkp和Δki的模糊规则表，可以得到Δkp和Δki的输出曲面如图6所示。

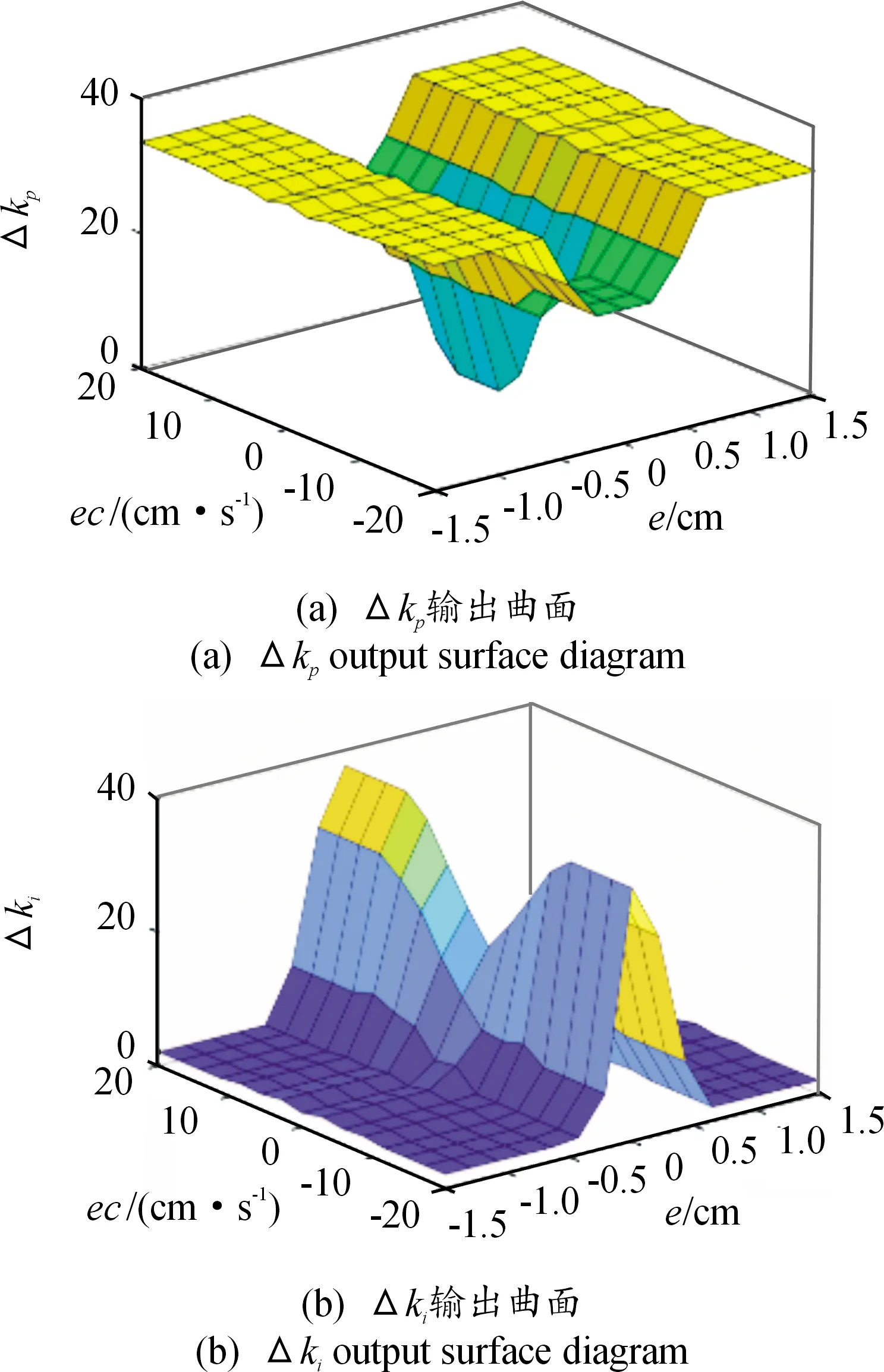
图6 Δkp和Δki输出曲面

将位置环替换为模糊PI控制器(初始参数为传统PI参数)，其他PI参数相同，α=0.75，β=0.25，Δ=0.01，空载运行，仿真时间设置成2.5 s，在1～1.5 s时加入10 N·m的干扰力矩。作动系统的输出位移如图7所示。

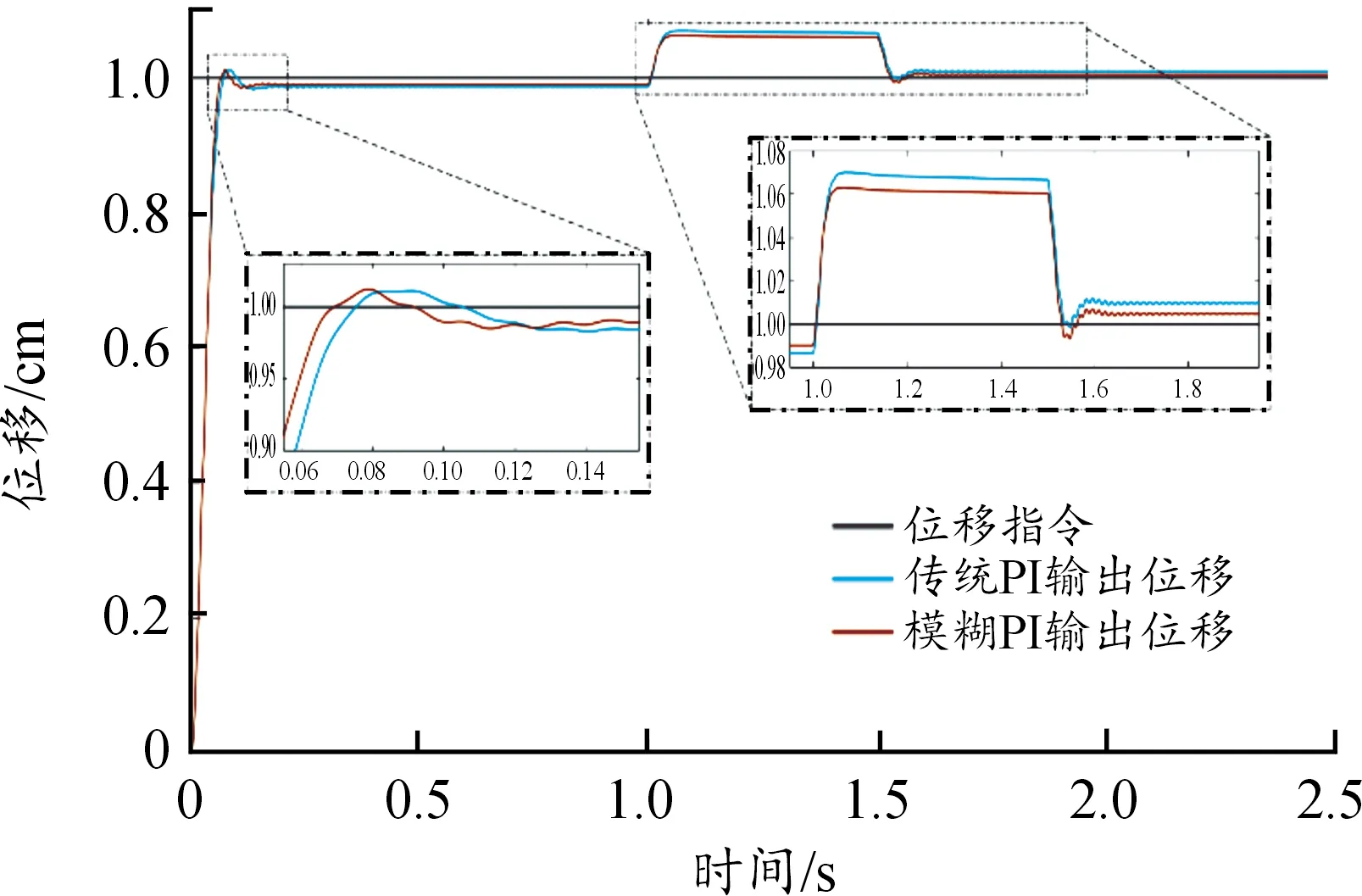
图7 模糊PI控制仿真的输出位移曲线

实验仿真的部分数据如表3所示。变化量等于传统PI与模糊PI的差值占传统PI值的百分比。

从图7与表3可以看出，模糊PI控制相比传统PI控制，上升时间减少8.33%，反应速度更快；稳态误差减小26.87%；加入干扰后，位移偏差减小10%，抗干扰能力变强。

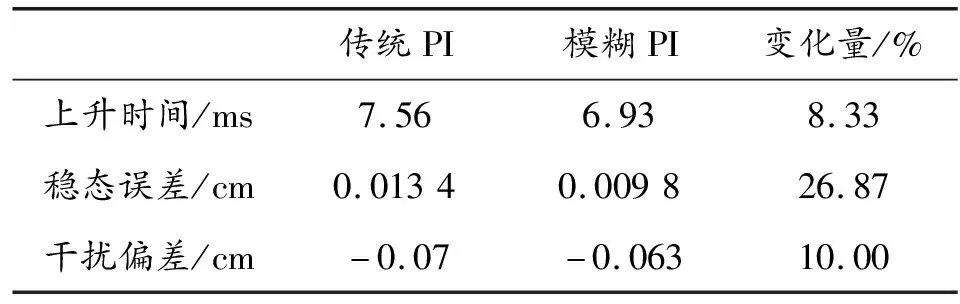
表3 模糊PI仿真结果参数

图8是仿真过程中模糊推理的输出量Δkp和Δki。

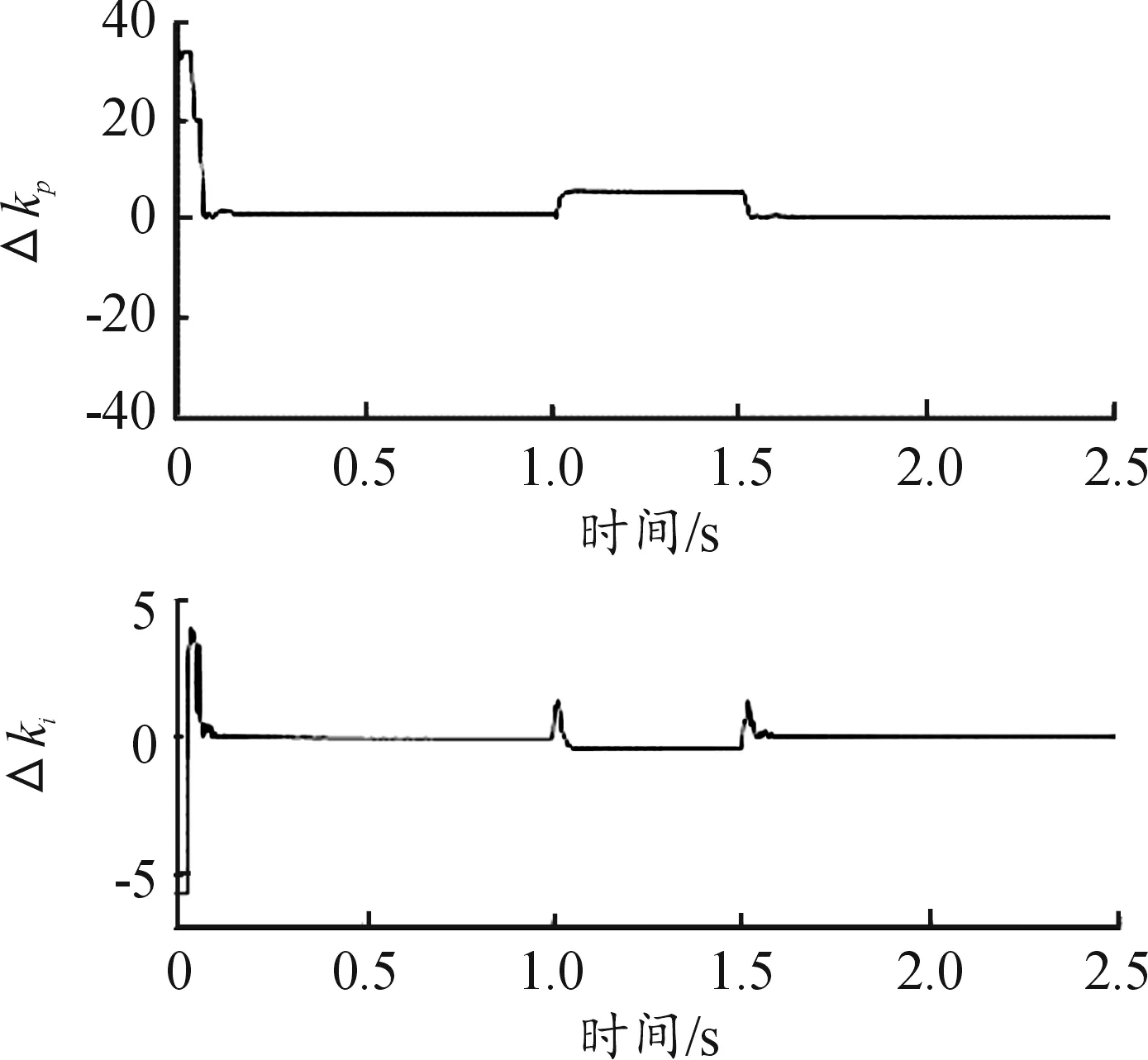
图8 模糊推理输出量Δkp和Δki

4.2 模糊PI-ANN控制仿真

将速度环的传统PI控制换成所设计的RBF神经网络，其中γ=5 000、p=21.9、Kp=1 140，其他仿真条件不变。作动系统输出位移如图9所示。

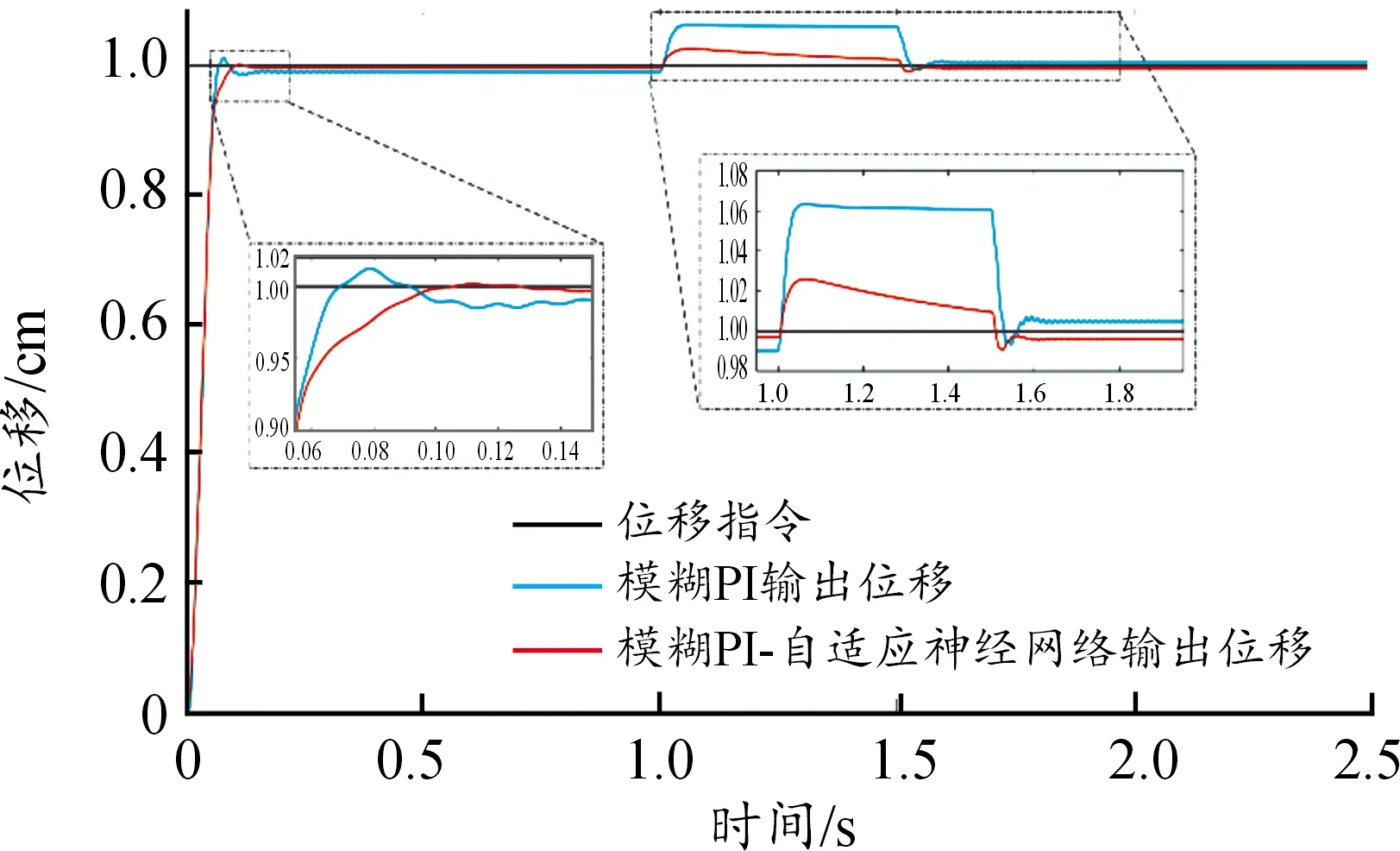
图9 模糊PI-ANN控制仿真的输出位移曲线

模糊PI-ANN控制系统仿真部分数据如表4所示。变化量等于传统PI与模糊PI-ANN的差值占传统PI值的百分比。

从图8与表4可以看出，在已有模糊PI控制的作动系统中，在速度环中所设计的自适应神经网络几乎无超调，平滑进入稳态，稳态误差减小76.87%，但是上升时间增加了39.68%；加入干扰时，位移偏差减小62.86%，明显提升了抗干扰能力且恢复稳态的时间更短。

图10表示了RBF神经网络仿真过程中的高斯隶属函数和自适应权值的估计值。

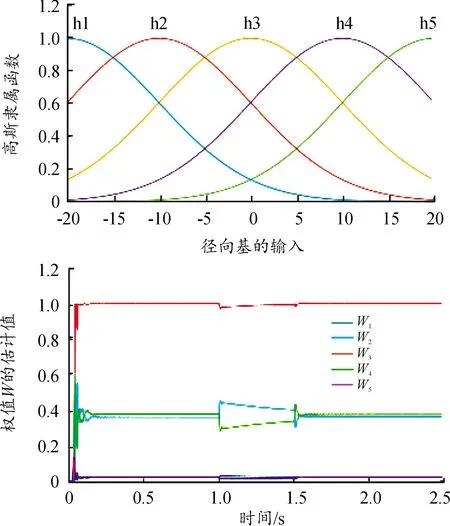
图10 高斯隶属函数与自适应权值的估计值曲线

5 结论

本文将智能控制中的模糊逻辑与RBF神经网络应用到机电作动器控制中，提出了模糊PI-ANN控制策略。根据PMSM传统三闭环控制系统，利用Matlab仿真软件构建基于传统PI、模糊PI和模糊PI-ANN控制策略的仿真模型。仿真结果表明，与传统PI控制和模糊PI控制相比，本文提出的模糊PI-ANN控制方法明显提高了机电作动器的位置跟踪性能，响应几乎无超调，稳态误差更小，稳态误差减小76.87%，抗干扰能力更强，位移偏差减小62.86%，恢复稳态的时间更短。下一步工作将是搭建实物模型，实现控制方法并进行实验，以使控制方法更加完善。