基于PBM算法的冲击波载荷数值模拟研究

张绍彦，王显会，彭 兵，孙魁远，沙康康，谢 渊

(南京理工大学 机械工程学院，南京 210094)

1 引言

近年来，军用战术车辆在战场上面对来自地雷的威胁日益增加，爆炸产生的冲击波载荷会对装甲车辆和乘员造成严重伤害[1]，开展装甲车辆抗爆分析、设计与防护日益成为关注的热点问题。爆炸试验具有高成本、耗时等特点，因此数值模拟方法被广泛应用于爆炸载荷的研究。

目前，多材料任意拉格朗日-欧拉(MM-ALE)算法结合流固耦合(FSI)算法模拟爆炸冲击波传播是公认的模拟爆炸的方法，国内外学者也对ALE算法可靠性进行了大量研究[2-4]。该方法兼具了Lagrange算法与Euler算法的优点，对于固体材料，允许节点和材料共同运动、变形；而对于流体材料，网格节点固定不变[5]。该方法能够处理网格畸变问题，可以更加精确地描述结构之间接触滑移面，但是在地雷爆炸情况下，高能炸药通常埋藏在土壤中，土壤与结构物相互作用的影响不容忽视[6-8]。为了提高ALE算法模拟结果的准确性，一般需要建立大量的空气和土壤单元，会造成计算效率低下，同时，拉格朗日-欧拉算法中的接触问题极易造成计算的不稳定。

因此，国内外学者开发了基于粒子的算法来提高计算效率与稳定性[9-11]，如光滑粒子法(SPH)、粒子爆炸法(PBM)和离散元法(DEM)等。李利莎等[12]运用ALE和SPH两种算法对炸药在钢筋混凝土板表面爆炸进行了模拟分析，对比分析了2种算法的优缺点，发现SPH算法可以更为逼真地模拟爆轰效果并且可以有效地防止能量泄漏。L.Olovsson等[13]最先将PBM算法应用到爆炸仿真中。随后，Teng等[14]对PBM算法进行了改进，并在LS-DYNA中实现了该算法，模拟了一系列固支钢板近距离爆炸，同时将仿真结果与实验结果进行比较，发现该方法具有高精度，较ALE方法具有更好的计算经济性。

本文以固支钢板空爆试验为对标对象，采集爆炸冲击下钢板中心最大变形数据，分别开展PBM算法、ALE算法数值仿真模拟，验证PBM算法计算结果的准确性以及计算的高效性。同时对PBM算法进行进一步研究，探究炸药粒子数量、空气粒子数量对计算结果的影响，为寻求模拟爆炸载荷的最优算法提供理论依据。

2 粒子爆炸法

粒子爆炸法(PBM)的本质是对基于分子动力学理论[15]的粒子法的改进，在该算法中，当粒子发生碰撞时，平动动能和转动动能之间的平衡不再成立，但对整个系统来说，系统达到平衡态时，平动动能和转动动能之间满足统计学上的平衡规律。此外，该算法为了更好地描述气体在极端压力和温度下的行为，考虑了协体积效应，使得爆炸产物在高温高压下的气体行为更加精确。

2.1 分子动力学理论

分子动力学理论起源于1738年Daniel Bernoulli提出的一种理论，即气体压强是大量气体分子与器壁碰撞的结果。以动力学理论为出发点，James Clerk Maxwell得出了一个非常简洁的表达式，表示热平衡时的分子速度分布：

(1)

式中：f(v)是分子速率的概率密度函数，其中：v为分子速率；M为摩尔质量；R为通用气体常数；T为温度。

分子动力学理论是对气体分子及其相互作用(在微观水平上)的研究，该理论揭示了气体宏观热学性质和过程的微观本质，推导出了理想气体定律(宏观关系)，给出了宏观量与微观量平均值的关系。该理论基于以下假设：① 分子之间的平均距离远大于分子自身的尺寸大小；② 存在热力学平衡，即分子处于随机运动；③ 分子可以看作质点，运动时遵守牛顿运动定律；④ 分子-分子和分子-结构相互作用是完全弹性的碰撞；⑤ 除碰撞的瞬间外，分子间的相互作用力可忽略不计。图1 为粒子-粒子相互作用示意图[16]。

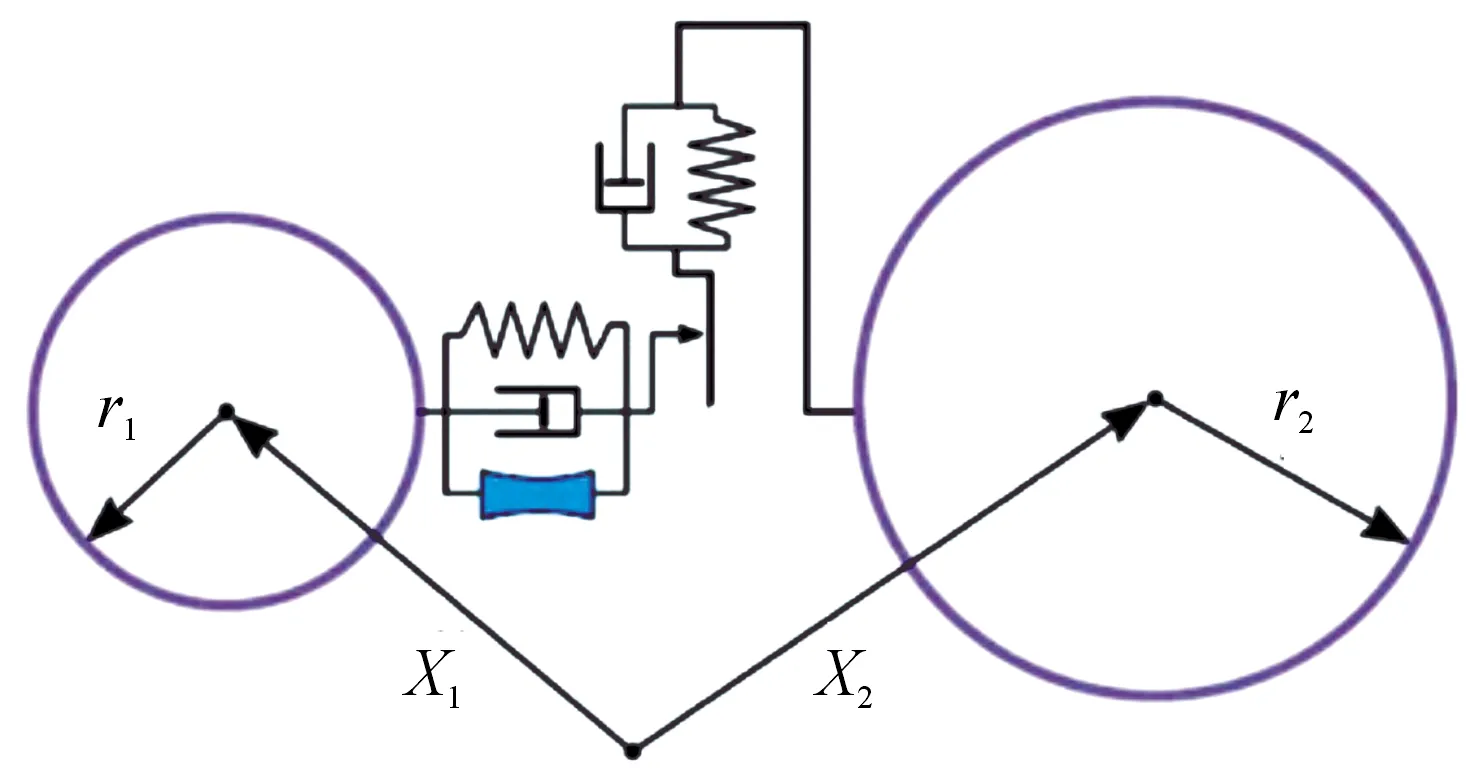
图1 粒子-粒子相互作用示意图

2.2 粒子爆炸法在LS-DYNA中的应用

每克爆炸物根据分子量的不同可以达到1022～1023分子的数量级，由于无法对爆炸场中的每一个分子进行独立建模，为了提升仿真过程中的计算效率，对分子动力学理论进行以下假设：

1)粒子是刚性的，并且呈球形；

2)每个粒子代表许多分子，分子数通常为1015～1020，具体取决于应用；

3)对于每个单独的粒子，平动动能Wt和转动动能WS之间的平衡关系由γ=Cp/Cv确定，其中Cp，Cv分别表示在恒定压力和恒定体积下的热容。平衡假定为:

(2)

Ws是每个粒子的一个总的标量变量，因此，粒子没有为转动/振动分配任何自由度。当粒子撞击移动的结构时，Wt将发生变化，而Ws则假定不受影响，因此，Ws和Wt之间的比值将发生改变。当2个粒子碰撞时，它们之间的能量将重新分配以维持Ws、Wt之间比值的恒定，以确保总能量和动量的平衡。粒子的半径可以动态调整以获得合理的平均自由程，由于粒子质量是恒定的，半径过小会导致压力波不能传递，半径过大会使气体作用偏离理想气体定律。此外，随着粒子半径的增大，粒子之间接触计算也会使仿真的成本增加。

3 固支钢板抗爆轰试验

3.1 试验布置

为验证PBM算法仿真精度，开展了固支钢板在TNT空爆条件下的试验研究，试验台架如图2所示，固支钢板长宽尺寸1 500 mm×1 500 mm，厚度4.5 mm，周边等距离开孔，试验台架上、下方框与钢板对应位置开孔，通过螺栓将钢板完全固定，台架上方框厚度为10 mm，下方框厚度为25 mm，在钢板正下方布置变形梳测试钢板在冲击波载荷作用下的中心点最大挠度，变形梳由梳齿和梳背两部分组成，梳齿长度呈阶梯状分布，梳齿材质为易产生塑性变形的铝合金，变形梳如图3所示，变形梳位置如图4所示。为增强试验台架刚度，内部设置多条加强板，以减小试验过程中台架发生大的破坏影响试验结果。试验中爆炸物为2 kg圆柱形TNT药柱，高径比为0.92，药柱直径119.2 mm，高109.8 mm，爆炸品位于靶板中心的正上方，药柱下表面距离钢板上表面300 mm，采用中心起爆方式，试验实物布置如图5所示。

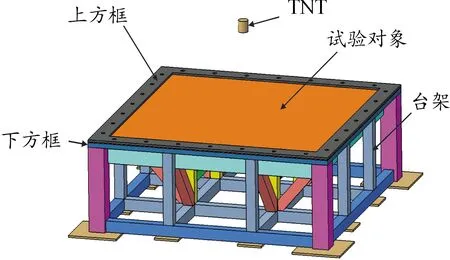
图2 台架示意图

图3 变形梳示意图

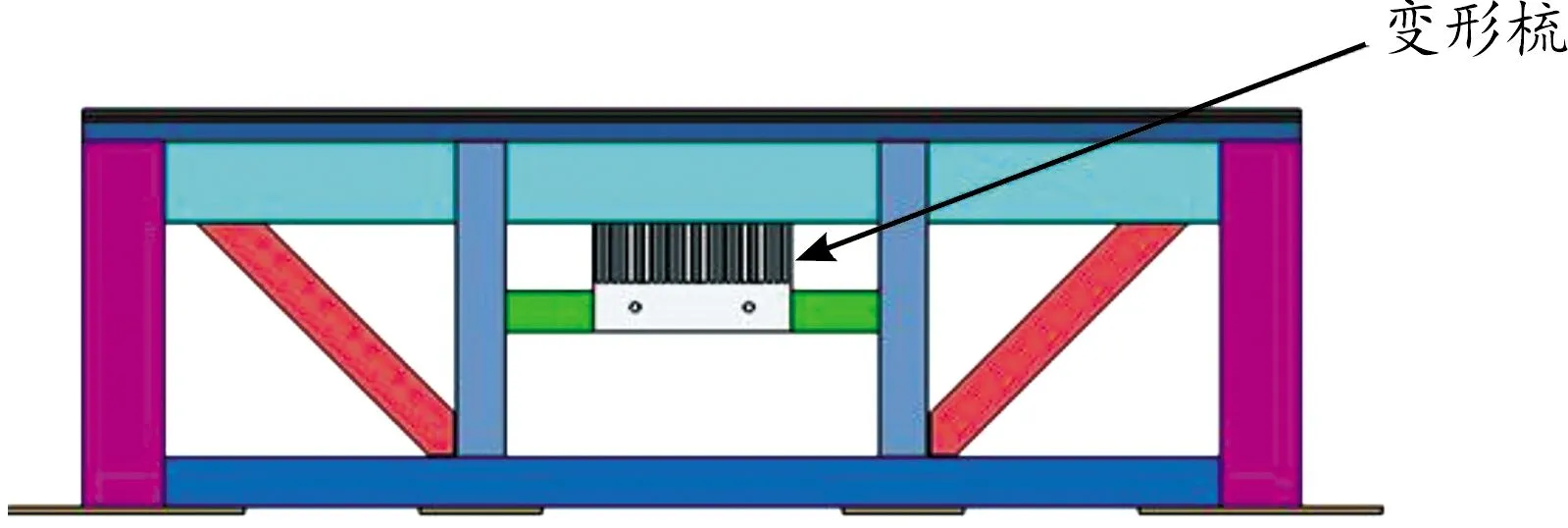
图4 变形梳位置示意图

图5 试验实物布置图

3.2 试验结果

爆炸试验后台架基座无明显损坏，四周固定螺栓未脱落，钢板的试验及仿真结果如图6所示，回收置于钢板底部的变形梳如图7所示，通过对比变形疏变形前与变形后梳齿的变形测量得钢板中心点最大挠度为60.1 mm。

图6 钢板变形示意图

图7 试验后变形梳图

4 有限元爆炸仿真研究

采用LS-DYNA非线性动力学仿真软件，分别使用ALE算法和PBM算法、SPH算法对试验工况进行了数值模拟。

4.1 ALE有限元模型

由于试验后台架基座无明显损坏且固定螺栓未脱落，台架的约束边界未遭到破坏，因此在仿真中简化台架模型，保留夹具与靶板，建立炸药、空气、靶板与夹具模型，如图8所示。炸药和空气单元均为实体并采用Euler算法，空气域为长方体，尺寸为1.6 m×1.6 m×1.1 m，为研究空气网格尺寸对仿真计算效率及精度的影响，空气单元尺寸分别采用10 mm、15 mm、20 mm。夹具、靶板均为实体并采用Lagrange算法，单元尺寸为10 mm。炸药、台架包含在空气域内，模型中炸药、空气域台架的相互作用通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID定义，耦合方式采用罚函数法，夹具与钢板之间的接触采用*CONTACT_AUTOMATIC_SINGLE_SURFACE关键字定义，在空气域四周设置无反射边界条件(*BOUNDARY_NON_REFLECTION)模拟空气的无限空间，防止爆炸冲击波到达边界发生反射影响仿真结果。

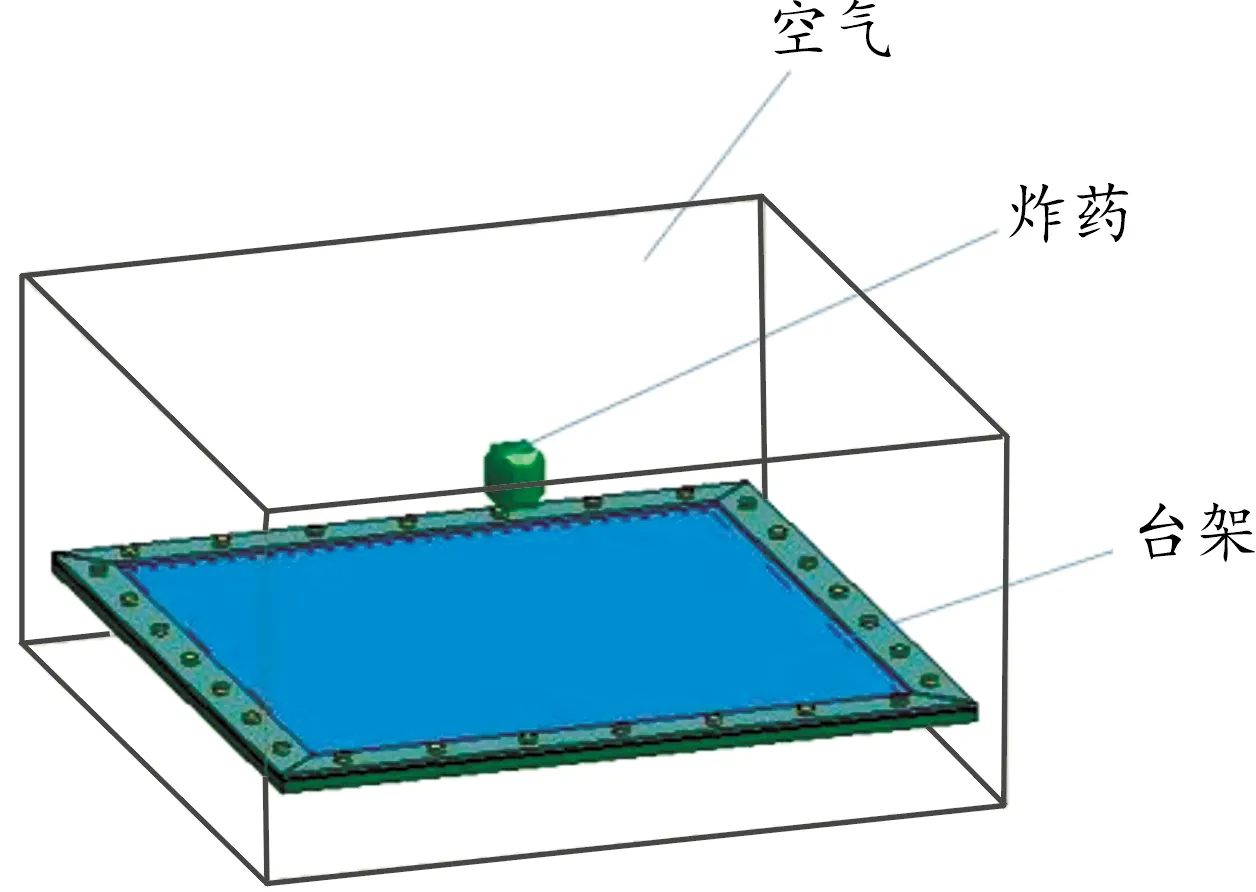
图8 ALE有限元模型示意图

靶板采用高强防弹钢，其材料的本构关系采用*MAT_SIMPLIFIED_JOHNSON_COOK模型描述，如公式(3)所示，利用拉伸试验机和霍普金森实验装置分析材料的静、动态力学性能，获得材料的主要参数见表1所示。

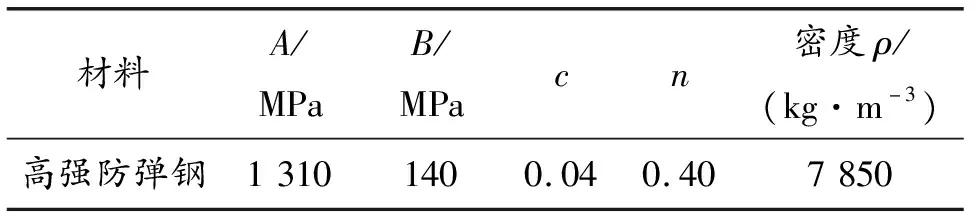
表1 高强防弹钢主要材料参数

(3)

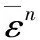
高能炸药的本构关系采用*MAT_HIGH_EXPLOSIVE_BURN描述，状态方程采用*EOS_JWL，方程如式(4)所示，使用初始体积法(*INITIAL_VOLUME_FRACTION_GEOMETRY)定义炸药形状与位置，其材料参数[17]见表2所示。

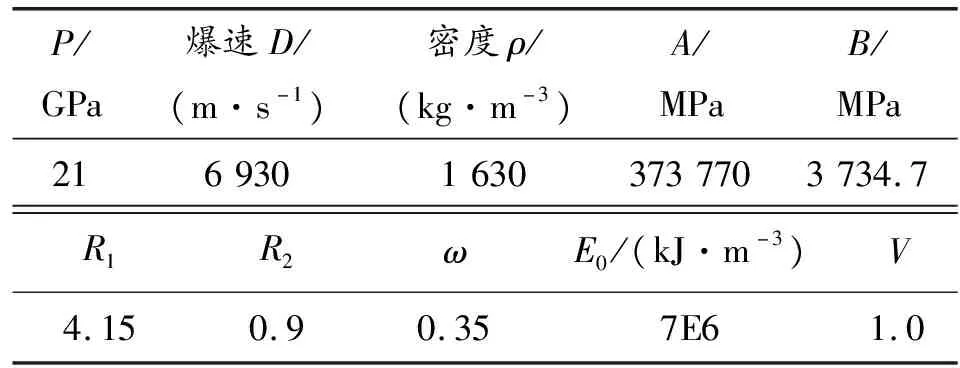
表2 炸药主要参数

(4)

式中：P为爆轰压力，A、B、R1、R2和ω为炸药特性参数；V为初始炸药相对体积；E0为炸药单位体积初始内能。

空气的本构关系采用*MAT_NULL描述，其状态方程采用*EOS_LINEAR_POLYNOMIAL，状态方程多项式如式(5)所示，空气的主要参数[18]见表3所示。

表3 空气参数及状态方程系数

P=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)E0

(5)

式中：P为空气压力，C0、C1、C2、C3、C4、C5、C6为状态方程多项式参数，E0为空气单位体积初始内能。

4.2 SPH模型建立

图9为SPH仿真模型，仿真模型中的钢板与夹具的单元类型、尺寸、材料与ALE模型一致，区别在于SPH算法中忽略了空气的影响，同时将TNT高能炸药离散为光滑粒子，炸药药柱直径119.2 mm，高109.8 mm，一共离散为10 000个SPH粒子，模型中炸药与台架之间的相互作用采用关键字*CONTACT_AUTOMATIC_NODES_TO_SURFACES定义，为研究SPH粒子数对仿真计算效率及精度的影响，SPH粒子数分别设置为5 000、10 000、50 000。在SPH算法中容易出现渗漏现象(大量的光滑粒子在没有接触力的情况下穿透了靶板)，因此采用以下两点措施以改善这种状况：① 细化炸药模型，将高能炸药离散为更多SPH粒子，并且进一步细化靶板有限元模型；② 通过接触控制与时间步长控制，增加靶板中单元的接触罚函数刚度系数和SPH单元属性中的平滑步长系数以及减小质量缩放系数等方法是SPH粒子与台架之间的接触更加严格。

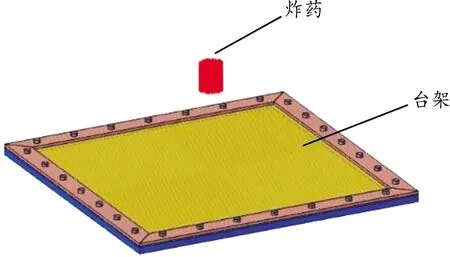
图9 SPH仿真模型示意图

4.3 PBM模型建立

图10为PBM仿真模型，高能炸药和空气均采用粒子模拟，通过*DEFINE_PBLAST_GEOMETRY创建炸药的几何形状，定义其特征尺寸与局部坐标参数，在此基础上生成所需要的圆柱形炸药。利用关键字*PARTICLE_BLAST建立TNT的材料模型，同时该关键字还定义了爆炸粒子与拉格朗日网格的相互作用方式，定义PBM模型中高能炸药的爆速、初始内能和密度等参数见表4所示。此外，该关键字还定义了符合理想气体定律的空气粒子，夹具与钢板的单元类型、尺寸与ALE模型中相同。

图10 PBM仿真模型

表4 高能炸药材料参数

4.4 仿真结果及分析

由于PBM不是基于连续介质力学，在数值模拟的过程中粒子是非可视的，只能看到定义的粒子点云的运动，如图11所示。

所有仿真模型计算时间均设置为3 ms，使用同一台计算服务器进行求解计算，ALE模型中研究空气网格尺寸对计算精度的影响，将空气单元尺寸分别设置为10 mm、15 mm、20 mm。PBM模型中研究炸药粒子数量(Np)对计算精度的影响，在空气粒子数为0的条件下分别设置了5 000、10 000、50 000、100 000个炸药粒子。同时为了研究空气粒子数(Na)对计算精度的影响，在炸药粒子为50 000的条件下分别设置了0、20 000、50 000、100 000、200 000个空气粒子。各仿真模型计算结果统计见表5所示。

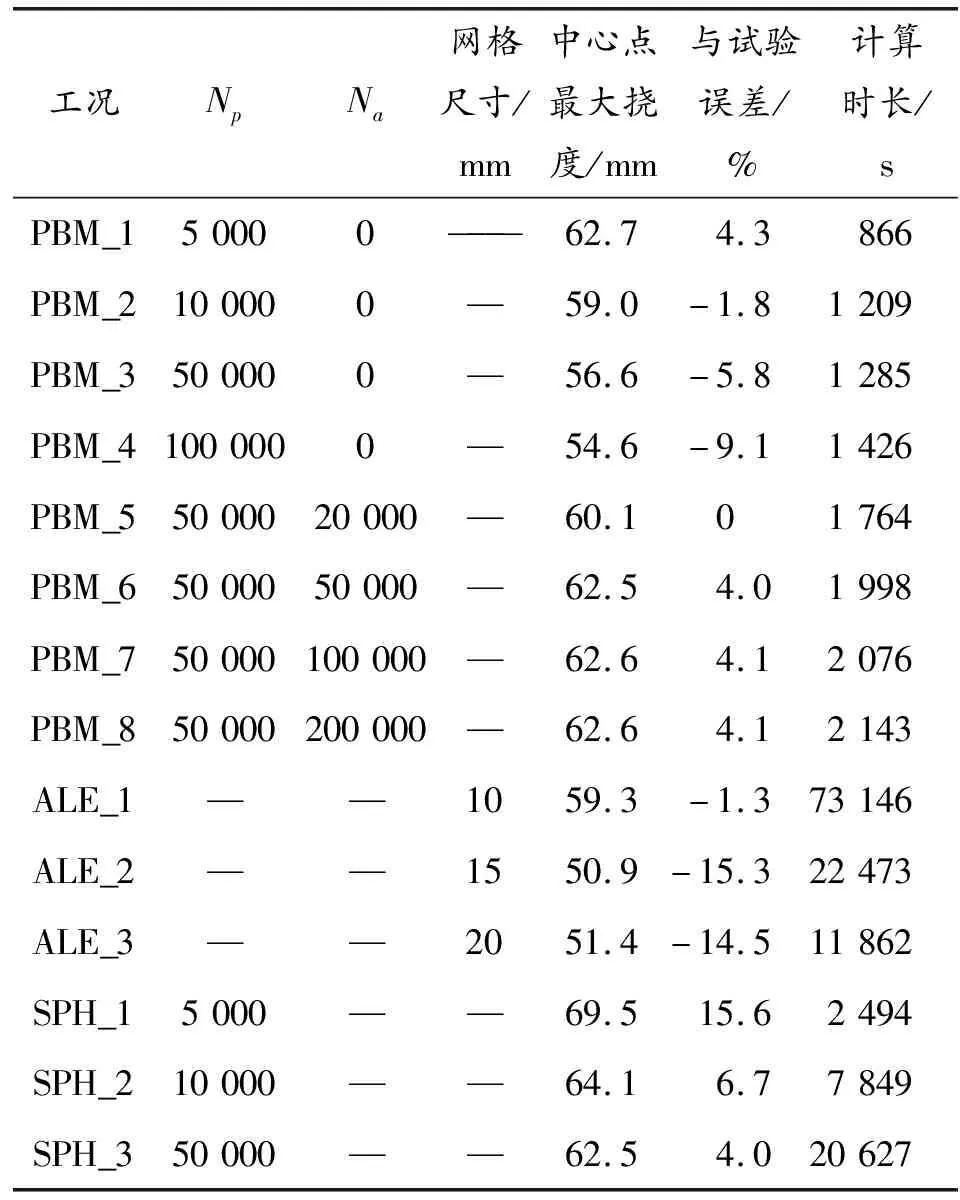
表5 仿真结果与试验结果

图12表示了不同空气网格尺寸的ALE模型仿真结果与PBM模型仿真结果。从图11和表5中可以得出：ALE模型和PBM模型数值模拟所得到的靶板中心点挠度随时间变化的趋势一致，ALE模型的数值模拟所得到的靶板中心点挠度低于试验测量值，PBM则略高于试验测量值。值得注意的是，对于网格尺寸较大的ALE_2和ALE_3工况，数值模拟所得的结果明显低于试验测量值，误差分别达到了15.3%、14.5%，而对于网格尺寸较小的ALE_1工况，数值模拟所得到的结果和试验结果的误差较小，仅有1.3%，同PBM模型数值模拟得到的结果有较好的一致性。此外，还可以发现2种算法模型中靶板中心点达到最大挠度的时间不同，ALE模型中靶板中心点达到最大挠度的时间在爆炸开始后1 ms左右，而PBM模型则明显较晚，靶板中心点达到最大挠度的时间在爆炸开始后2 ms左右，2种算法中台架的初始结构响应一致，相同的结构响应过程出现在了不同的时间，表明在结构响应方面PBM算法的仿真过程具有滞后性。

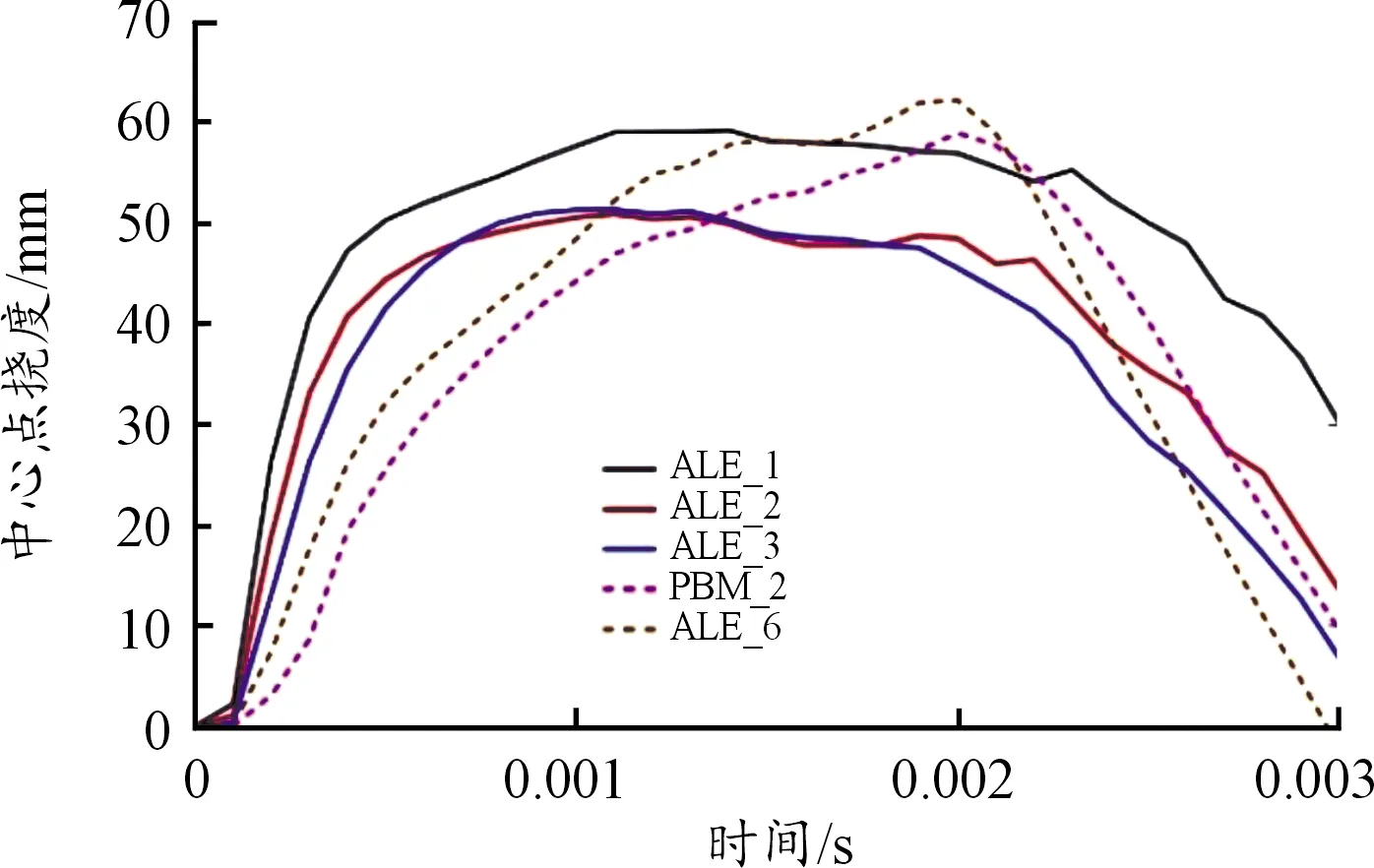
图12 ALE模型与PBM模型仿真结果曲线

图13为不同SPH粒子数的SPH模型与PBM模型的仿真结果，由于SPH算法中忽略了空气的影响，仿真所得到的结果略高于ALE算法与PBM算法的仿真结果。由图13可得：SPH算法与PBM算法数值模拟所得到的靶板中心点挠度随时间的趋势大致相同，SPH算法与PBM算法的数值模拟所得到的靶板中心点挠度都略高于试验值，对于光滑粒子数较少的SPH_1和SPH_2工况，数值模拟所得到的结果误差较大，分别达到了15.6%和6.7%，而对于粒子数较多的SPH_1工况，数值模拟的误差较小，为4.0%，因此提高SPH粒子数有利于提高仿真结果的精确性。

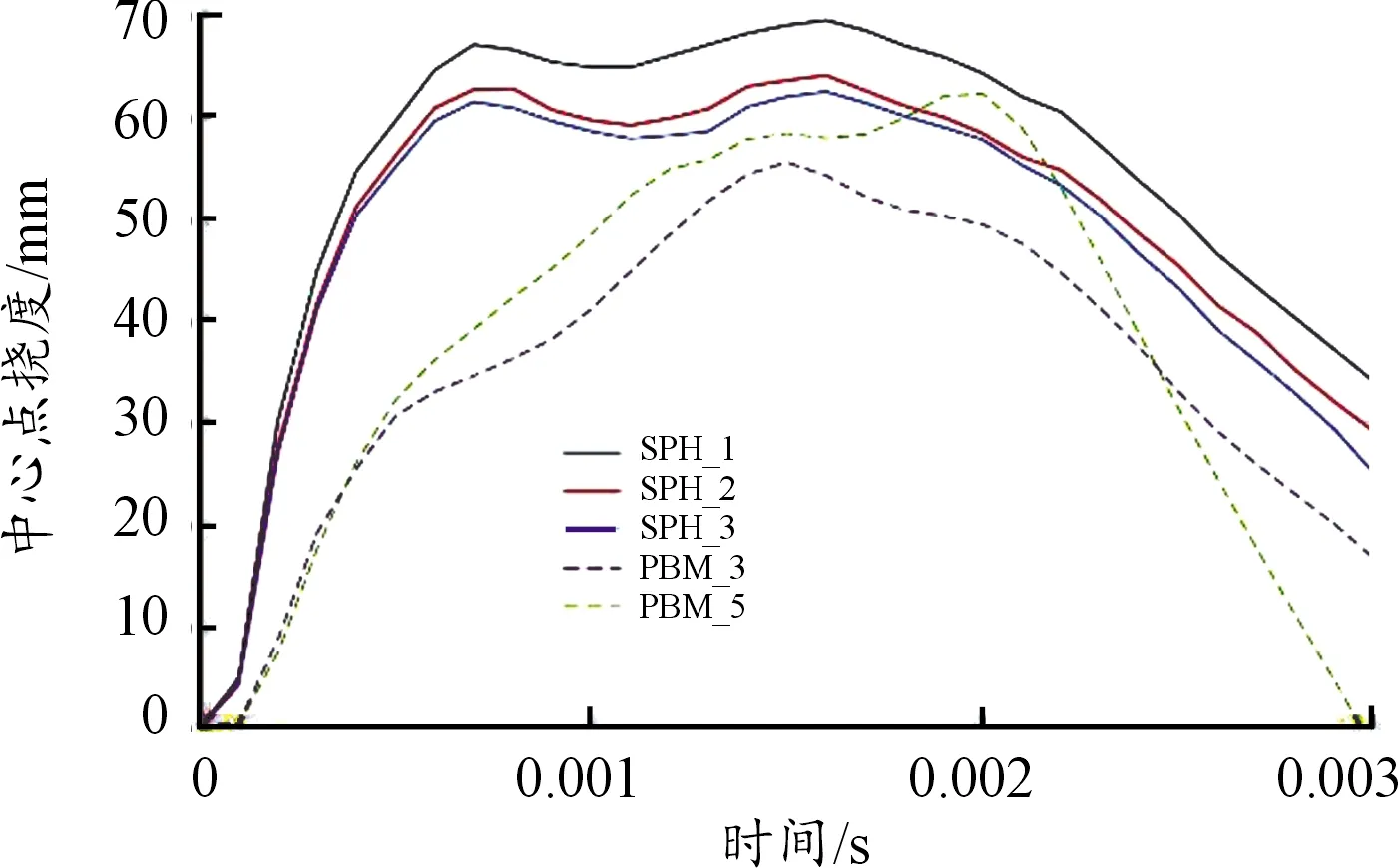
图13 SPH模型与PBM模型仿真结果曲线

为了研究PBM模型中炸药粒子数量对仿真结果的影响，在空气粒子为0的情况下，进行了PBM_1到PBM_4四种工况的数值模拟，4种工况靶板的中心点挠度随时间的变化趋势如图14所示。由图14可知：4种工况的数值模拟结果中靶板中心点挠度随时间变化的趋势大致相同，都是先增大至最大值，然后逐渐减小，但是爆炸粒子数量对靶板中心点挠度达到最大值的时间有一定影响。此外，从图中还可以得出：炸药粒子数对数值模拟结果的影响较大，靶板中心点的最大挠度随着炸药粒子数的增加而减小，并逐渐趋向于一个稳定值。

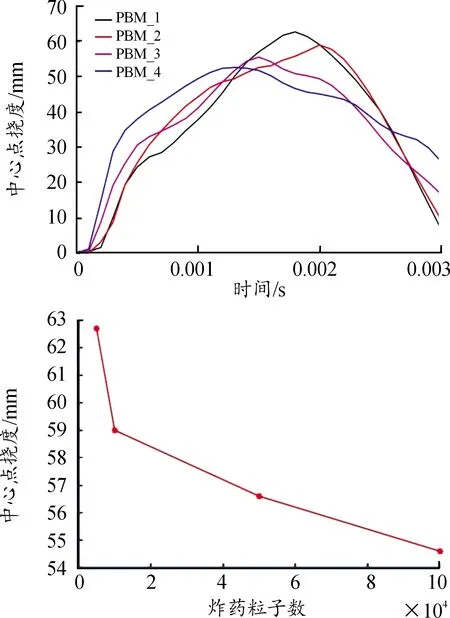
图14 中心点挠度随炸药粒子的变化曲线

为了研究PBM模型中空气粒子数量对数值模拟结果的影响，进行了PBM_3、PBM_5、PBM_6、PBM_7、PBM_8五种工况的数值模拟，五种工况靶板的中心点挠度随时间的变化趋势如图15所示。由图15可知：从整体上看，五种工况靶板的中心点挠度随时间变化的趋势大致相同，靶板的中心点挠度随着时间先增大后减小。此外，在炸药粒子数量一定的情况下，靶板中心点挠度的最大值随着空气粒子数的增加而增加，并且逐渐趋近于稳定值，在空气粒子数大于50 000时，PBM模型中空气粒子数对数值模拟的结果的影响很小。

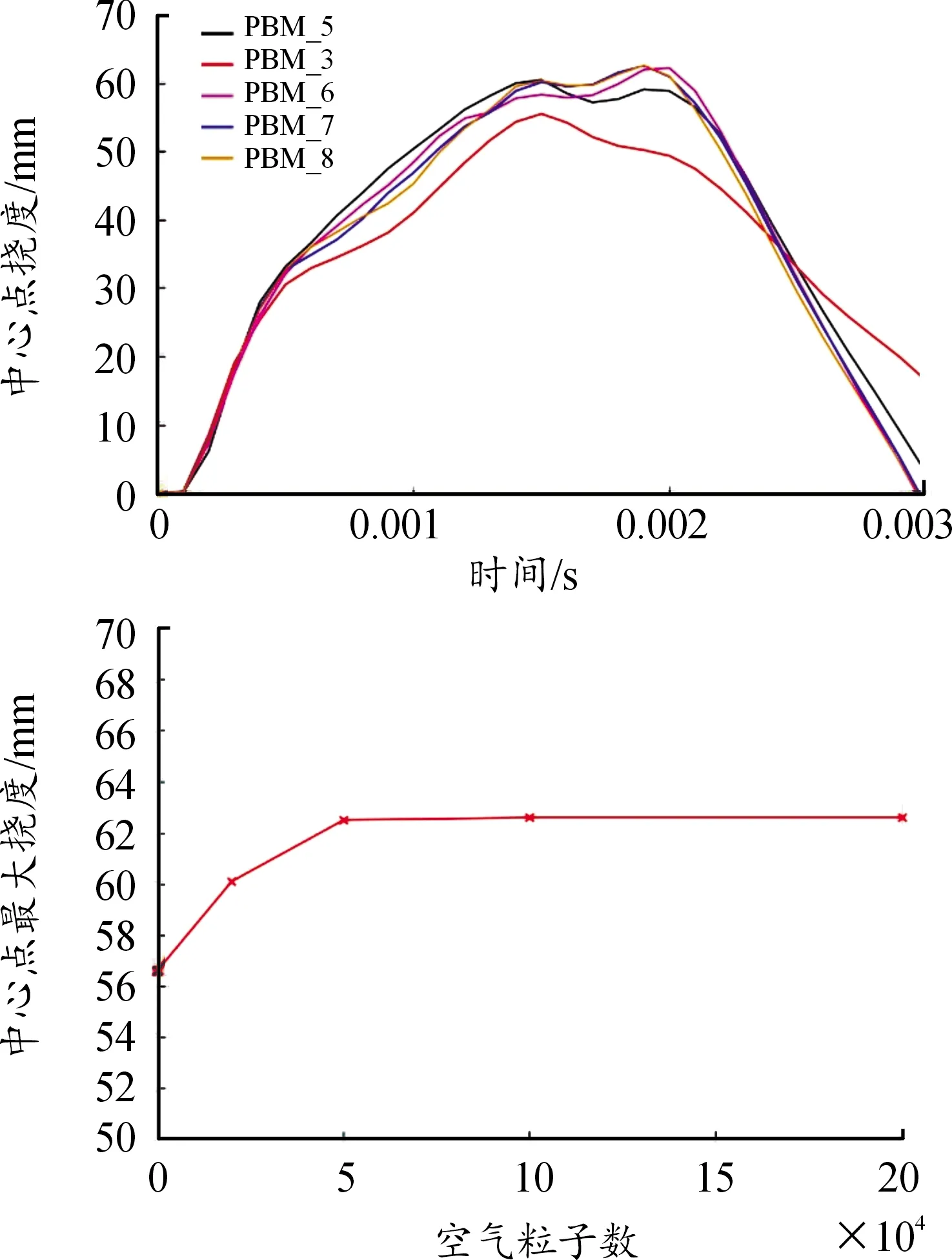
图15 中心点挠度随空气粒子数的变化曲线

对比PBM算法、ALE算法SPH算法的计算效率，分别统计了各工况计算时长，见表5所示。从整体来看，ALE模型和SPH模型的计算时长远大于PBM模型的计算时长，网格尺寸对ALE数值模拟结果的影响较大，为提高计算精度减小网格尺寸会造成计算时长大幅增加,SPH粒子数对SPH模型的计算时长影响较大，且SPH算法的计算成本随着SPH粒子数的增加而增加，PBM模型的计算时长随粒子数的增加而增加，但远小于ALE模型与SPH模型，并且粒子数对靶板中心点的最大挠度影响较小。

5 结论

1)ALE模型中网格尺寸对数值模拟结果影响较大，减小网格尺寸可以有效提高计算精度，当空气网格尺寸与结构网格尺寸接近1:1时，仿真结果与试验结果误差较小，与PBM模型计算结果具有良好的一致性，与ALE算法相比，在结构响应方面PBM算法的仿真过程具有滞后性；SPH算法和ALE算法的计算精度相似,并且当SPH粒子数的较多时，仿真误差较小，与PBM算法的一致性较好。

2)PBM模型中，在空气粒子数量一定的情况下，炸药粒子数对数值模拟结果的影响较大，靶板中心点的最大挠度随着炸药粒子数的增加而减小，并逐渐趋近于试验值。

3)PBM模型中，在炸药粒子数一定的情况下，靶板中心点的最大挠度随空气粒子数的增加而增加，并且当空气粒子数大于50 000时，空气粒子数量对数值模拟结果的影响较小，靶板中心点挠度的变形状况趋于稳定。

4)在误差较小的情况下，与ALE算法、SPH相比，PBM算法可以大大的节省计算成本，此外，PBM模型中，计算成本随着粒子数的增加而增加并且增加炸药粒子所增加的计算成本远大于增加空气粒子所增加的计算成本。