局部凹坑织构化径向滑动轴承流体动力润滑数值分析
纪敬虎,周莹超,田朋霖,陈天阳,何玉洋
(江苏大学,江苏 镇江 212013)
滑动轴承是船舶、航空、电力和机械等工程领域的基础通用件,对整个旋转机械的稳定性有着重要影响,径向滑动轴承安全稳定运转的关键性因素就是润滑油膜[1],油膜承载力和压力分布是研究轴承特性的重要参数。
表面织构技术作为一种改善机械零件摩擦学性能的有效手段,已经得到广泛应用[2-3],并有望成为未来轴承结构设计的一个重要组成部分[4]。Tala-Ighil等[5]通过优化织构参数、调整织构配置,从而改善了球面凹坑织构轴承表面的摩擦学性能。随后,Tala-Ighil 等[6]研究了织构位置对滑动轴承性能的影响,数值结果表明,在接触区域合理布置织构范围,可以改善轴承的主要性能。Li 等[7]采用数值法研究了凸起织构对摩擦学性能的影响,揭示了轴颈轴承的摩擦系数和偏心率随凸起宽度和高度的变化规律。由此可见,通过合理布置织构区域和位置,控制织构的几何参数,是改善轴承摩擦学性能的有效方法[8-9]。
目前,众多学者的研究热点在于织构参数对滑动轴承油膜承载力和压力分布的影响[10-12],结合轴承结构参数和工况条件等综合因素对润滑油膜承载机制的研究尚不多见,而轴承表面织构和轴颈偏心的综合效应影响滑动轴承动压润滑性能[13]。本文研究了径向滑动轴承的流体动力润滑特性,基于雷诺边界条件[14],建立了凹坑织构化径向滑动轴承流体动力润滑理论模型。利用松弛迭代法[15],求解了油膜承载能力和油膜压力,研究了轴承偏心率和凹坑几何参数等综合因素对油膜承载能力的影响规律。
1 理论模型
1.1 几何模型
轴承计算坐标如图1 所示,O1为轴承中心;O2为轴颈中心;xO1y是周向坐标系;z是轴向坐标;U为轴承与轴颈相对滑动速度;偏位角ψ为O1O2与载荷F之间的夹角;φ为从O1O2开始测量的油膜位置角;RB为轴承半径;RJ为转子半径;偏心率ε=e/c(e为偏心距,c为半径间隙);h0为任意位置的油膜厚度;Fr和Ft分别为油膜力的径向分量和切向分量;hp为织构深度;rp为织构半径,φs、φt控制周向织构范围。图2 中,B为轴承的宽度,D为转子直径。
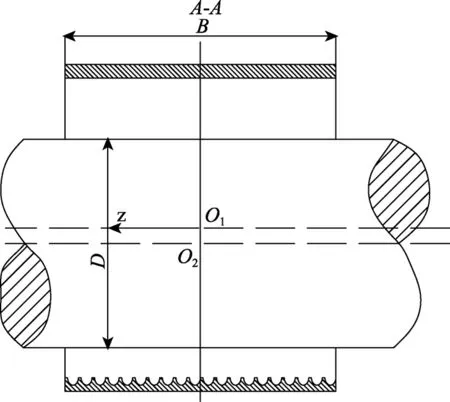
图2 有限长径向滑动轴承剖面[17]Fig.2 The cross section of finite length journal bearing[17]
光滑径向滑动轴承的间隙函数[14]为:

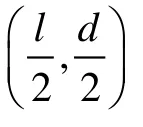

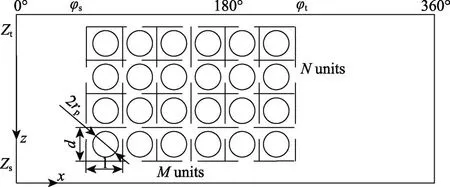
图3 凹坑分布结构模型Fig.3 Dimples distribution structure model
凹坑织构化轴承的油膜厚度[11]为:
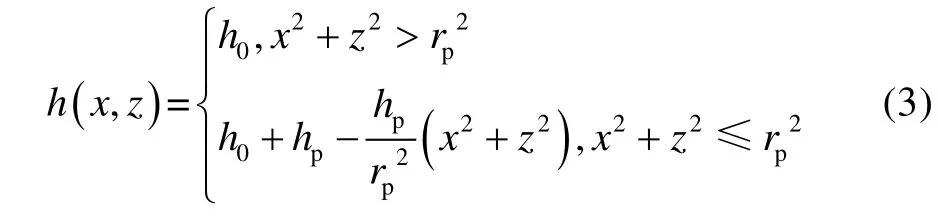
1.2 数学模型
假设:1)摩擦副表面被一层均匀的油膜分开;2)由于油膜厚度很小,不考虑压力沿膜厚方向的变化;3)润滑剂为牛顿流体,忽略其惯性力和体积力的变化[19]。由此得到不可压缩流体在稳态层流条件下的Reynolds 方程[20-21]为:
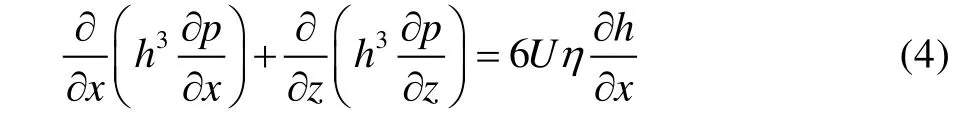
式中:h为油膜厚度;p为油膜压力;U为轴承与轴颈相对滑动速度;η为润滑油黏度。通过式(5)对二维雷诺方程实现无量纲化[22]。
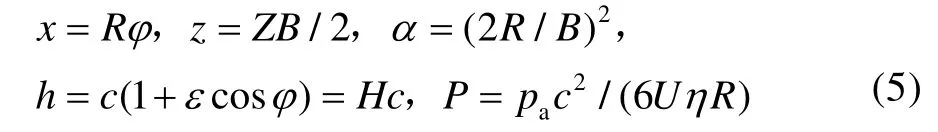
将式(5)代入式(4)后,得无量纲化Reynolds 方程:
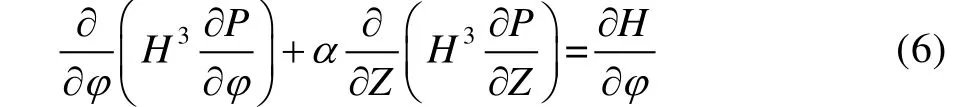
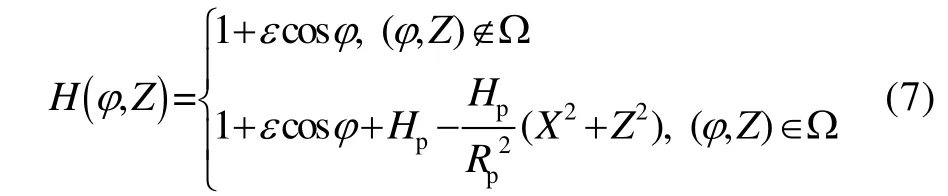
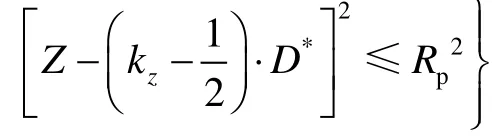
1.3 边界条件
本文数值计算过程中,采用的边界条件为[14,23]:
1)周向方向。Reynolds 边界条件,油膜终点的位置在求解过程中确定,在发散区域满足P=0,∂P/∂φ= 0。
2)轴向方向(如图2 所示)。在轴端面Z=1 处,P=0;在轴Z=0 处,∂P/∂Z= 0。
1.4 承载力
求得无量纲油膜压力分布后,在轴承工作表面进行数值积分[10,24],得无量纲油膜力F的径向分量Fr和切向分量Ft,分别为:
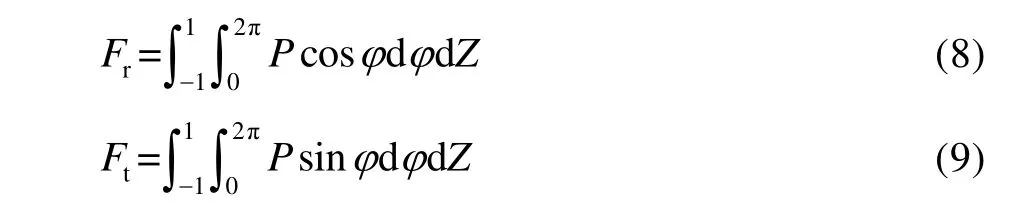
无量纲油膜承载力为:

1.5 摩擦力
当轴承固定时,轴颈转动的滑动轴承表面周向方向的剪切力τ为[10,24]:

由于油膜在滑动轴承内非连续,分为承载区和非承载区。hb为破裂时的油膜厚度,则油膜承载区摩擦力F1的无量纲表达式为:
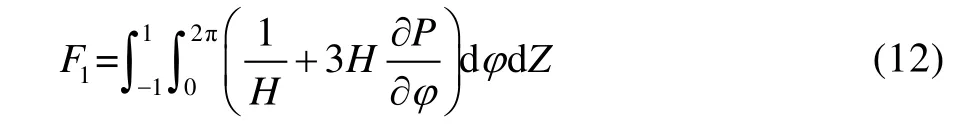
油膜破裂区的摩擦阻力为:

则完整滑动轴承圆周方向上的无量纲摩擦力f为:

2 数值求解方法及有效性验证
采用有限差分法将式(7)离散化,然后利用Gauss-Seidel 松弛迭代方法计算,流程如图4 所示。有限差分法[15,20]是将连续问题离散化:将求解域用有限个网格节点代替;将微分算子离散化。在网格节点上求得近似解,从而把微分方程的定解问题转化为代数方程的求解问题。
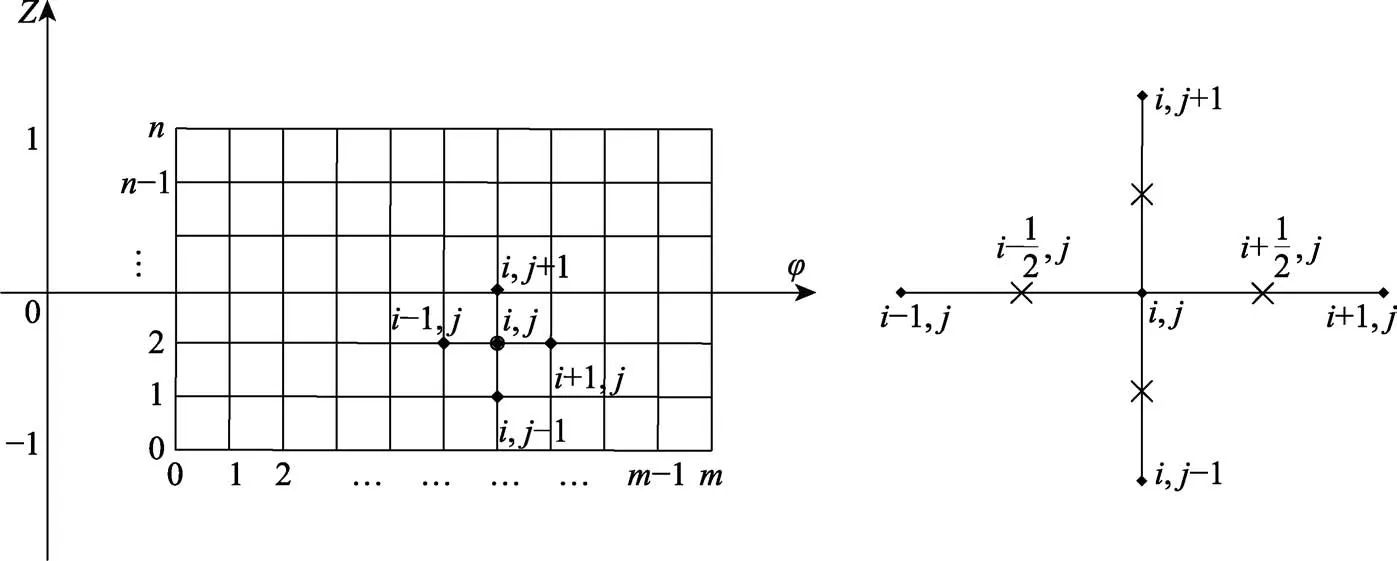
图4 差分网格Fig.4 Finite difference mesh
求得圆周方向和轴向方向油膜压力的二阶导数,并整理得:

Gauss-Seidel 松弛迭代方法是根据节点(i,j)周围4个半整数点的压力值来计算中间节点上的压力值,则式(15)变换为:
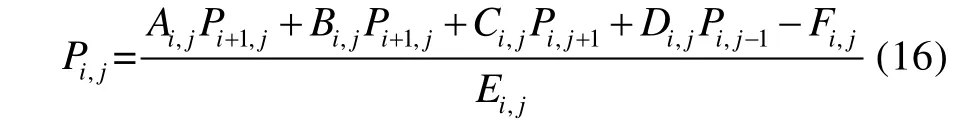
根据式(17)的收敛准则进行收敛性判断。
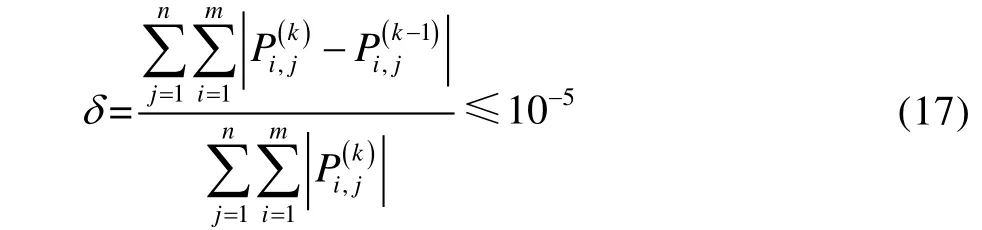
式中:k表示迭代次数。采用 MATLAB 软件对上述数值求解过程进行编程,计算流程如图5 所示。

图5 计算流程Fig.5 Calculation flow chart
为验证本文所编程序的可行性和正确性,计算了在不同偏心率和不同宽径比时的滑动轴承无量纲油膜承载力。从图6 中可以看出,宽径比一定时,滑动轴承的承载能力随着偏心率的增大而增大,尤其当偏心率接近于1 时,滑动轴承的承载能力显著增大并趋于无穷;当偏心率一定时,滑动轴承的承载能力随着宽径比的增大而增大。这其中的原因可能在于,当轴颈与轴瓦之间没有间隙时,两者之间的接触强度足够大,那么就可以认为滑动轴承所能承载的载荷可以无穷大。将所得的关系曲线与经典理论[25]的偏心率和油膜承载力的关系进行比较,可以看出,两者之间有相同的趋势。

图6 偏心率、宽径比与无量纲油膜承载力的关系曲线Fig.6 Relation curves of eccentricity, width-diameter ratio and dimensionless film carrying capacity
3 讨论与分析
径向滑动轴承参数及工况见表1。
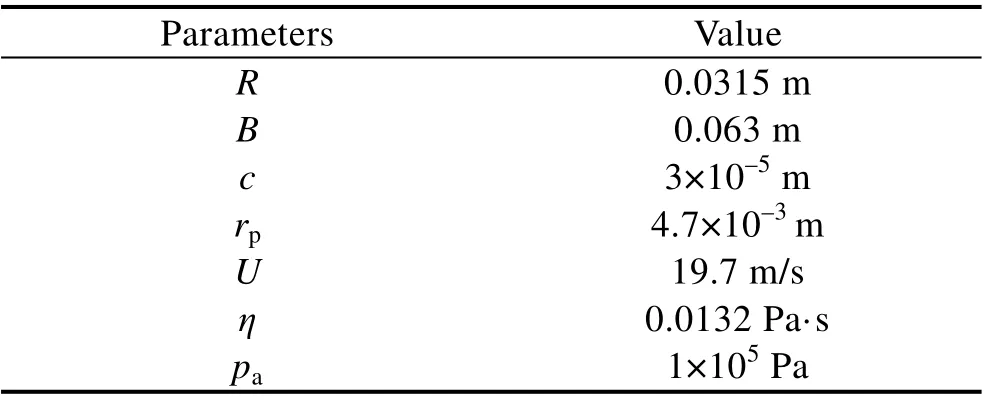
表1 工况与几何参数Tab.1 Operating conditions and geometric parameters
3.1 偏心率和凹坑深度对轴承特性的影响
将织构设置在轴承周向的第二角部分(180°~360°),轴向布满轴承宽度。保持滑动轴承的宽径比不变,计算偏心率和凹坑深度对轴承特性的影响。从图7 中可以明显看出,无量纲摩擦力随着偏心率的增大而增大。由于织构的存在,无量纲摩擦力随着凹坑深度的增加而减小,这表明凹坑起到了减摩作用。随着凹坑深度的增加,无量纲摩擦力之间的差异越来越小,这表明可能存在最佳凹坑深度,使得轴承性能达到最佳。随着偏心率增大,轴承和轴颈之间存在磨损,导致两者之间发生碰触,无量纲摩擦力增大。

图7 偏心率、凹坑深度和无量纲摩擦力的关系Fig.7 Variation diagram of different eccentricity, dimples depth and dimensionless friction force
凹坑深度与无量纲油膜承载力之间的关系如图8所示。结果显示,随着凹坑织构深度的增大,轴承承载力减小,并且织构化轴承承载力的差异很小。图8中还显示出,偏心率较小时,织构化轴承的承载能力略低于未织构轴承。这表明轴承表面经过织构化处理增加了膜厚,所形成的油膜压力变小,因而未织构轴承的油膜承载力较大。
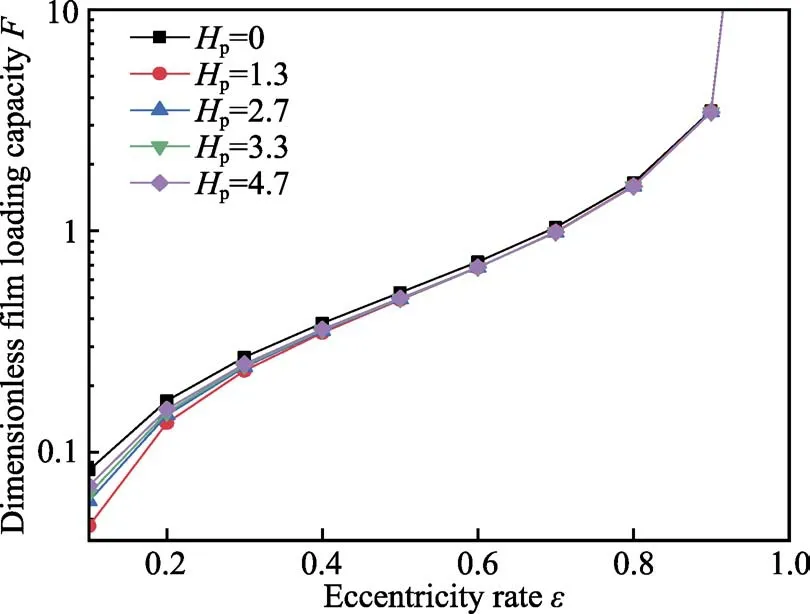
图8 偏心率、凹坑深度和无量纲油膜承载力的关系Fig.8 Variation diagram of different eccentricity, dimples depth and dimensionless oil film bearing capacity
当宽径比α=1,偏心率ε分别取0.3、0.5、0.8时,油膜厚度分布如图9 所示。当偏心率增大时,最小油膜厚度随之减小。在织构区域,油膜厚度随偏心率的增加而增大。但如果持续增大偏心率,这意味着轴颈和轴瓦直接接触,最小油膜厚度将变得更小。
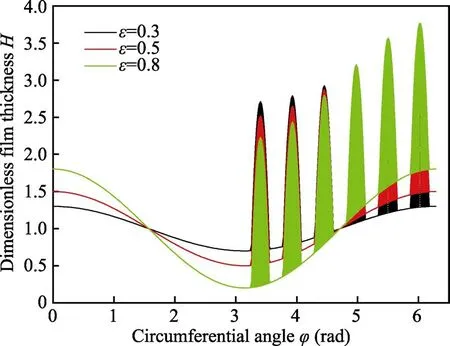
图9 不同偏心率下滑动轴承油膜厚度分布(α=1)Fig.9 Distribution of oil film thickness of journal bearing under different eccentricity (α=1)
油膜压力分布如图10 所示。随着偏心率的增大,油膜压力也随之增大。这是因为轴颈旋转将润滑油带入收敛间隙中,从而产生流体动压。在织构区域[π,2π]内,轴承与织构的楔形效应产生油膜压力,一个织构就是一个“微收敛楔”。即使在油膜发散区[π, 2π],也会产生一定的油膜承载力,提升轴承的承载能力。
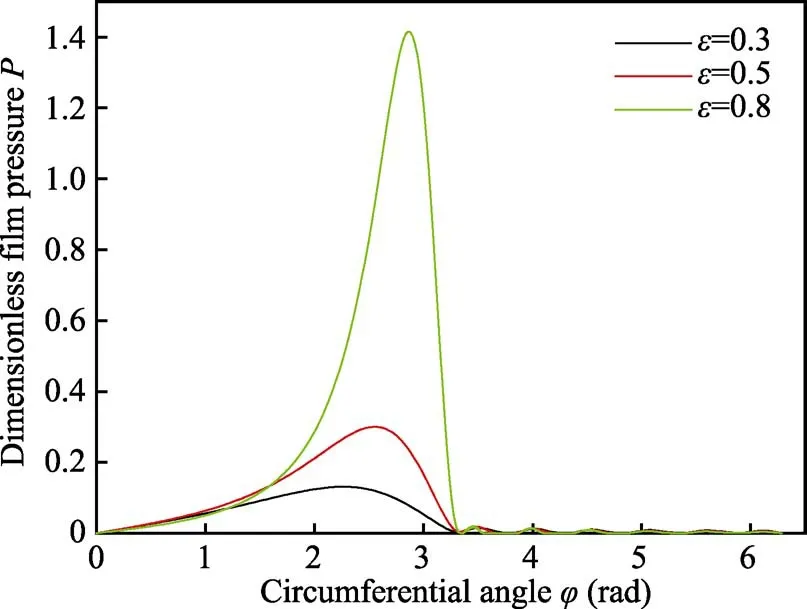
图10 不同偏心率下滑动轴承油膜压力分布(α=1)Fig.10 Oil film pressure distribution of journal bearing under different eccentricity (α=1)
3.2 织构面积密度对轴承特性的影响
织构的密度是影响轴承摩擦学性能的重要参数,对其流体动压润滑效果有重要影响。本小节研究了凹坑面积率对凹坑织构化径向滑动轴承润滑性能的影响。此时无量纲凹坑深度为Hp=2,织构数量分别为4×4、6×6、7×7、8×8。从图11a 中可以看出,织构化滑动轴承的无量纲摩擦力随着织构面积密度的增大而减小。在偏心率较小时,减摩效果较弱;而偏心率较大时,减摩效果较为明显。图11b 表明,无量纲油膜承载力基本保持不变。
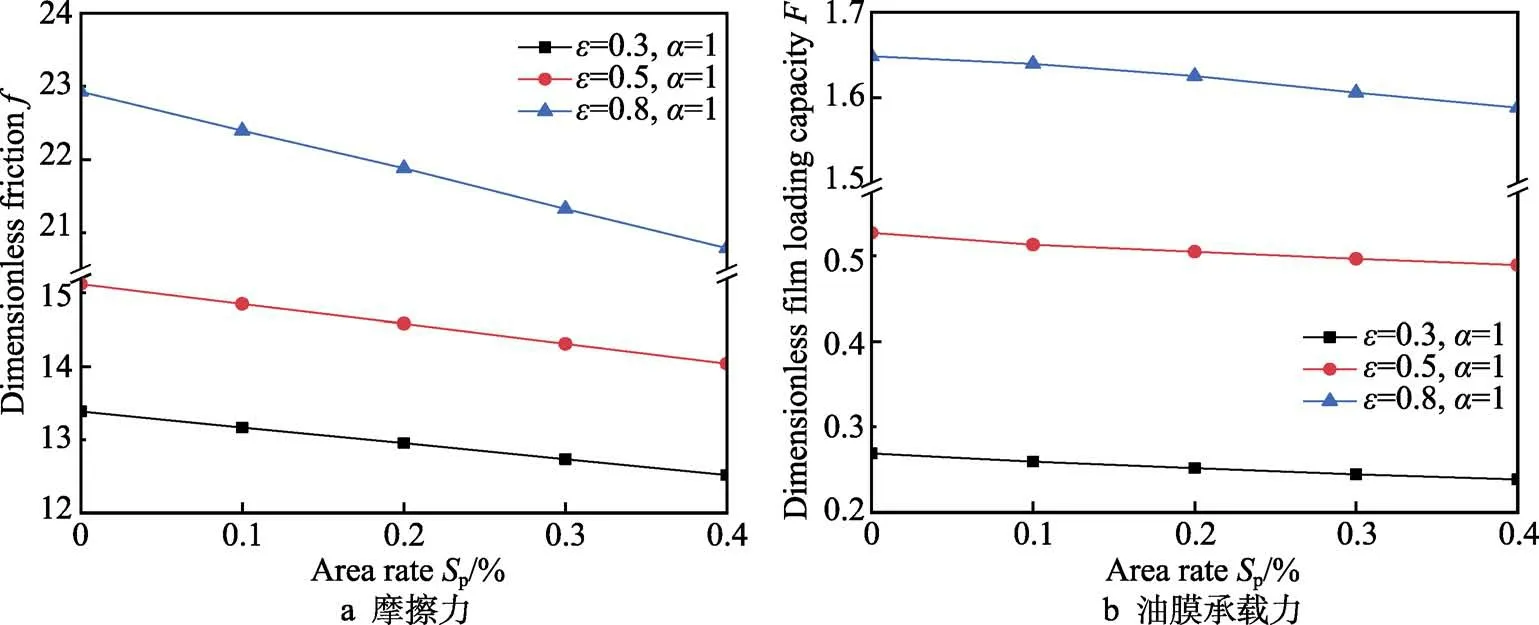
图11 面积率对轴承无量纲摩擦力、无量纲油膜承载力的影响Fig.11 Influence of area ratio on dimensionless friction force and dimensionless capacity of bearings
3.3 凹坑分布对轴承特性的影响
通过在轴承不同区域布置凹坑织构将会对轴承的润滑性能产生一定的影响,本文凹坑织构设置位置见表2。
表2 中4 种织构分布情况的油膜厚度如图12 所示。从图12 中可以看出织构的分布位置,位置1 为全织构,位置2 织构设置在轴承的油膜收敛区(升压区),位置3 横跨油膜收敛区和油膜发散区,位置4在油膜发散区(压降区)。

表2 凹坑织构的4 种分布位置Tab.2 Four distribution positions of dimples texture
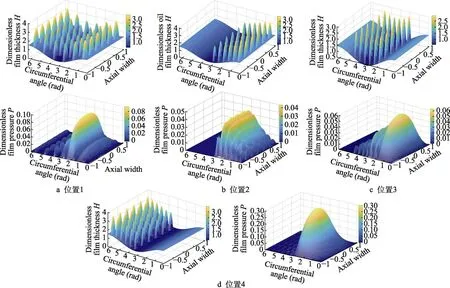
图12 4 种织构位置分布情况的无量纲油膜厚度和油膜压力Fig.12 Dimensionless oil film thickness and oil film pressure diagram of four texture position distributions
由表2 可见,未织构轴承的无量纲摩擦力最大,位置1 的无量纲摩擦力最小,位置2 和位置3 的无量纲摩擦力较为接近。在轴承无量纲承载力方面,未织构轴承最大,位置4 次之,位置1、位置2 和位置3较为接近。
4 结论
1)凹坑起减摩润滑作用,当凹坑深度变大时,轴承承载力随之减小,并且承载力之间的差异逐渐减小,可能存在最佳凹坑深度使得轴承减摩效果最佳。
2)随着面积率的增大,无量纲摩擦力逐渐降低,承载力基本不变。偏心率较大时,面积率对减摩润滑影响较大。
3)合理布置凹坑织构区域能提高承载能力,降低摩擦力,因而位置4 的织构位置方案最佳。

