基于模糊单神经元PID 的车载发射装置随动控制策略研究

王旭锋，牛远征，曾远帆，殷 翔，姜晓明

（1.南京理工大学 自动化学院，江苏 南京 210094；2.上海机电工程研究所，上海 201109）

0 引言

随着现代战争模式的迅速变化，战场上出现越来越多低空、超低空等进攻性武器，这就需要包括车载导弹发射车在内的防空系统具有快速、高精度、准确打击等能力。作为现代防空体系重要的一环，车载随动系统的响应速度、跟踪精度、鲁棒性等指标的优劣会直接影响武器系统作战效能的发挥。

对于发射车的随动系统而言，由于作战环境复杂多变，机械摩擦、外部扰动等因素持续存在，动静态性能也会发生很大变化。在跟踪目标的过程中，会产生动态滞后，目标速度变化越快，滞后越突出，精确的控制模型往往难以建立。因此，传统PID 控制已经不能满足现代战争模式的作战需求［1］。

多年来，许多学者致力于模糊PID、自适应PID、神经网络PID 等先进PID 控制的研究，用以克服传统PID 缺陷。其中，模糊PID 控制可以很好地应用于非线性时变系统，但是模型的建立需要大量的经验，在输入输出上受模糊集的影响较大，从而导致系统超调、响应慢等问题［2-4］。自适应PID 控制的好坏，取决于辨识模型的精确度，对于复杂系统是特别困难的［5］。本文提出一种将单神经元与模糊PID 控制相结合的位置随动控制策略，以两种控制方法优缺点互补为思路，运用神经网络控制与模糊控制理论，设计出相应的比例Kp、积分Ki、微分系数Kd的动态调整规则，实现PID 参数的自整定，以此提高系统的快速性、控制精度和干扰能力［6］。

1 车载随动系统组成及建模

1.1 车载随动系统组成

车载随动系统的控制对象为发射装置，其随动系统的基本组成如图1 所示。

图1 随动系统的基本组成Fig.1 Basic composition of the follow-up system

伺服计算机是随动系统的控制中枢，接收来自武控计算机发送的发射装置方位角、左/右发射架高低角控制指令，经坐标转换、拉格朗日插值、伺服控制、量纲转换等步骤，向驱动器发送转速控制指令［7］。交流（Alternating Current，AC）伺服驱动系统为发射装置的驱动机构，系统采用三相交流永磁同步电机，用于给发射装置提供动力力矩。驱动器接收到伺服计算机的转速控制指令后，经功率放大电路，形成驱动电机的电压，电机转动并通过减速器作用于发射装置。发射装置的实际位置通过测角装置发送给伺服计算机，最终形成随动系统的闭环控制［8］。

1.2 车载随动系统建模

1.2.1 交流伺服驱动系统建模

交流伺服驱动系统包含有速度环和电流环。速度环为外环，主要用于控制电机转速。速度环的反馈来自于电机编码器的旋变信号，经驱动器内部芯片解码后得到转速，由驱动器完成速度环的闭环控制。电流环为内环，主要用于控制电机电流，确保电枢电流在启动瞬间不超过允许值。电流环的反馈来自于驱动器内部安装在每相的霍尔元件，驱动器采样电流值后，完成电流环的闭环控制［9］。交流伺服驱动系统工作原理图如图2 所示。

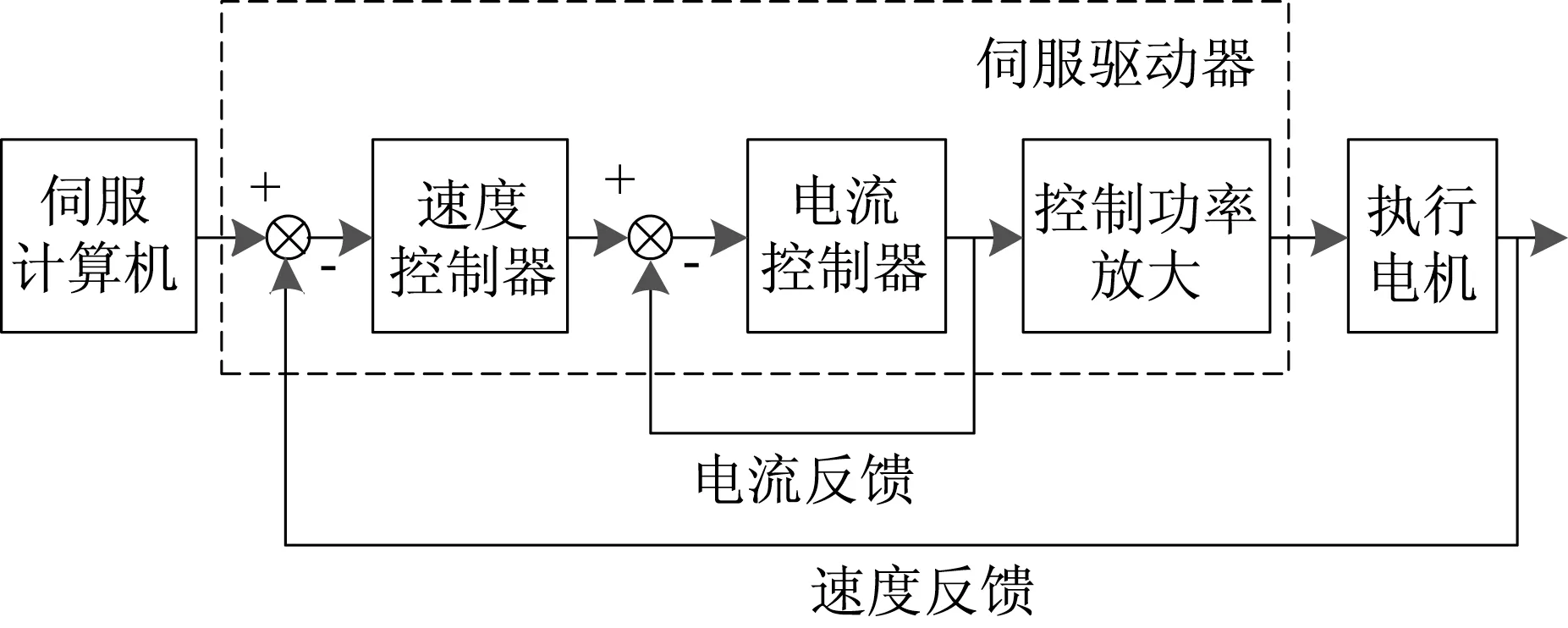
图2 交流伺服驱动系统工作原理Fig.2 Working principle diagram of the AC servo drive system

由于交流永磁电机内部电磁场关系较为复杂，建立数学模型比较困难。因此，在进行随动仿真时，一般用电枢电压控制的直流电动机进行。为了简化电机模型作如下假设：忽略磁场高次谐波影响、电枢回路电感、转子的绕阻、永磁体的阻尼，以及内部磁场的饱和效应和磁滞带来的损耗。这样驱动放大器就可近似成1 个比例环节，执行电机则简化为一阶惯性环节，旋变作为1 个积分环节［10］。由此可得到2 阶线性系统模型结构，如图3所示。

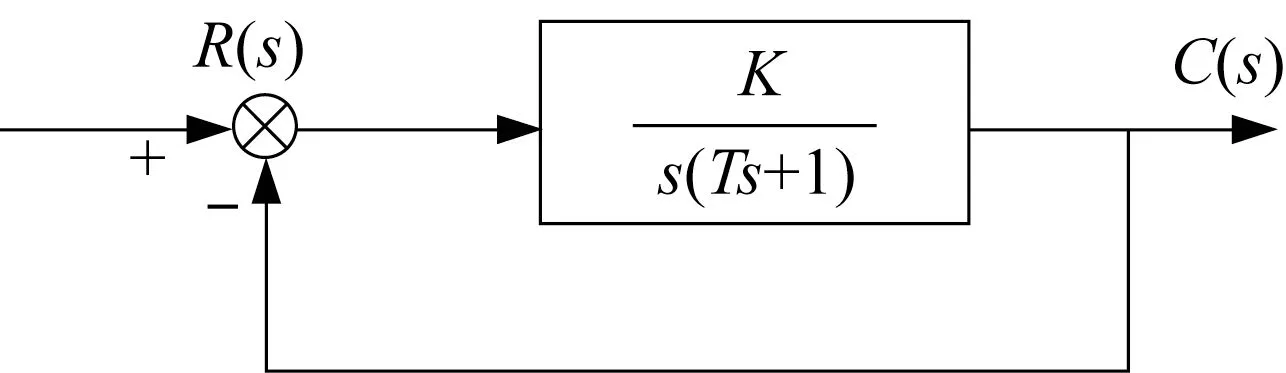
图3 交流伺服驱动系统等效结构Fig.3 Equivalent structure diagram of the AC servo drive system

图中，R(s)对应伺服计算机发送的给定转速，C(s)对应电动机的实际转速。电机参数、负载惯量以及黏性摩擦系数对参数K、T都有影响。由于参数在工程上难以直接测量和理论计算，一般常采用脉冲响应、阶跃响应等方法确定参数数值［11］。本文采用阶跃响应法对交流伺服系统进行辨识，即给驱动器发送适当幅值的阶跃信号，同时测量电动机的转速信号，得到速度环响应的超调量σ%和峰值时间tp。根据如下典型2 阶系统阻尼比ζ、无阻尼振荡频率ωn的公式：

可得到交流伺服驱动系统的传递函数为

采用上述方法，以某车载发射车的方位随动系统为例，多次测得方位随动系统的超调量与峰值时间，并求均值以后，根据式（1）、式（2）以及传递函数公式得到交流伺服驱动系统的传递函数为

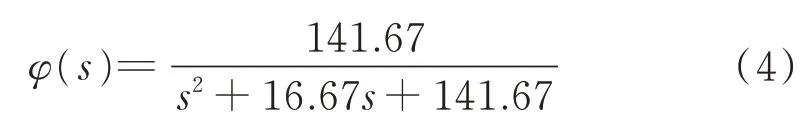
1.2.2 车载随动系统整体建模

根据车载防空武器随动系统的组成及工作原理，将随动系统分为位置环、速度环、电流环，其工作原理图如图4 所示。

图4 车载防空武器随动系统的工作原理Fig.4 Working principle diagram of the follow-up system for vehicle-borne air defense weapon

以某车载发射车的方位随动系统为例，减速器是齿轮组合结构，减速比r为120，考虑到角速度单位换算系数100，可得到随动系统从伺服计算机到转塔输出的转角部分的传递函数为

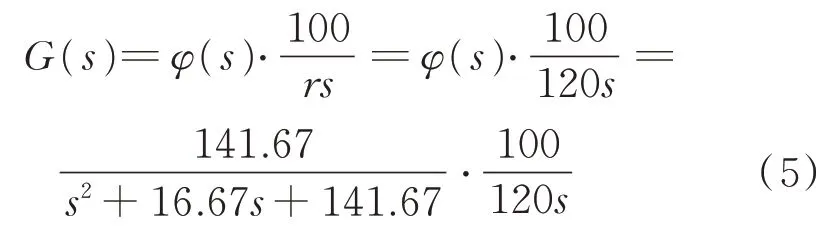
综上，随动系统可近似看成1 个含积分环节的3阶系统。

2 模糊单神经元PID 控制器

2.1 控制器整体设计

模糊单神经元PID 控制作用于位置环，运行在伺服计算机软件上。该控制以模糊PID 控制为主体，引入单神经元控制器实时调整参数。然后将两种算法融合后的kp、ki、kd作用于被控对象，其控制结构如图5 所示。

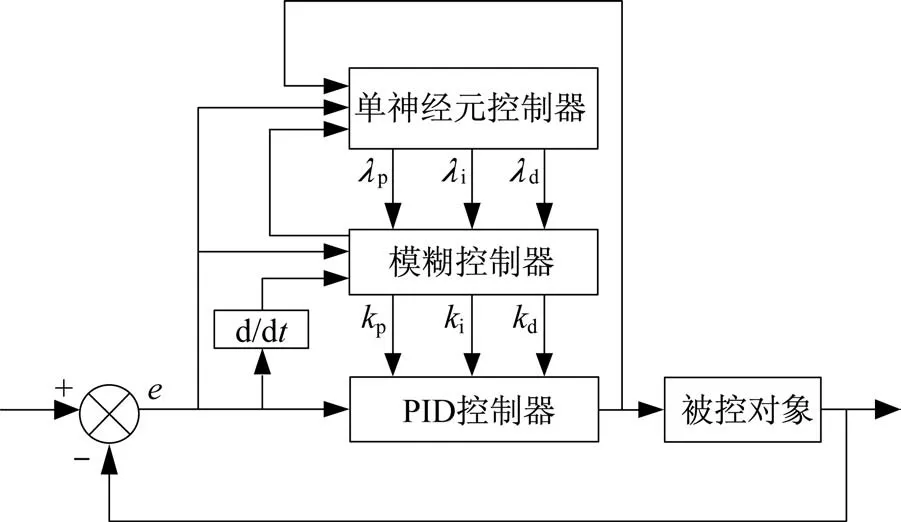
图5 模糊单神经元PID 控制结构Fig.5 Control structure of the fuzzy single neuron PID

2.2 模糊控制算法

用系统误差e和误差变化量ec作为模糊PID 控制输入，比例系数调节量ΔKp、积分系数调节量ΔKi、微分系数调节量ΔKd作为输出，利用模糊控制规则在线对PID 参数进行修改，以满足不同时刻的e和ec对PID 参数自整定要求［12］。

将模糊PID 控制输入e和ec的变化范围，定义为模糊集上的论域：e，ec=[-3，3]。其模糊子集为e，ec=[NB，NM，NS，ZE，PS，PM，PB]，子集元素分别代表“负大”“负中”“负小”“零”“正小”“正中”“正大”。对输入进行尺度变换后，使输入量映射在设定的论域内，目的是对输入模糊化。对输出而言，比例系数调节量ΔKp、积分系数调节量ΔKi、微分系数调节量ΔKd的论域分别设置为[-3，3]、[-1，1]、[-1，1]，ΔKp、ΔKi、ΔKd均服从正态分布。以比例系数调节量ΔKp为例，其隶属度函数如图6所示。

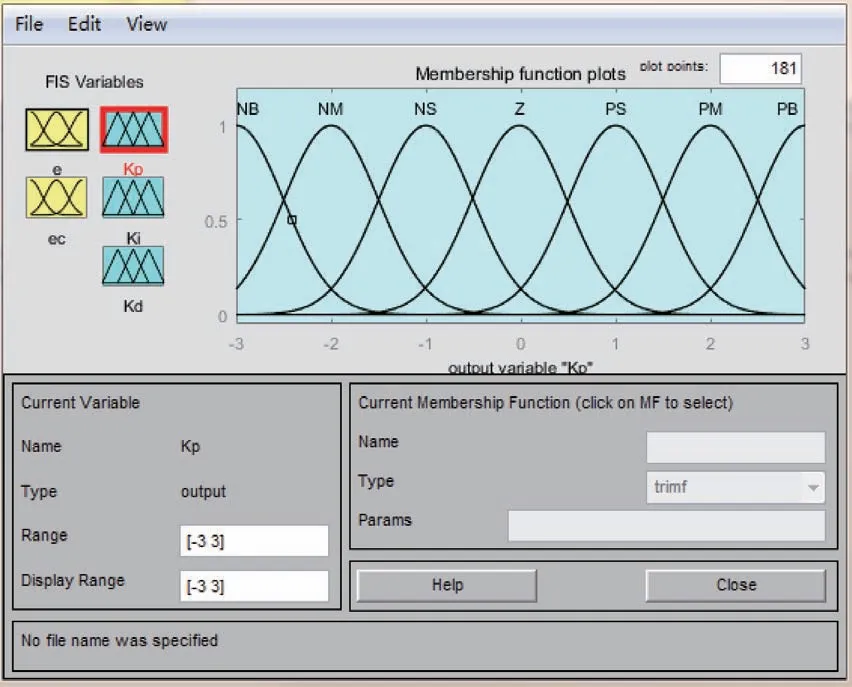
图6 隶属度函数设置Fig.6 Setting of membership functions

考虑到不同时刻，3 个参数对系统作用以及3 个参数之间的相互影响，模糊PID 控制在PID 控制的基础上对输入模糊化，并根据模糊规则进行模糊推理，查询模糊矩阵表进行参数调整。制定规则如下：当转塔执行角度偏转指令开始，为提高响应速度，增大比例系数，减小微分系数作用；在中后期，增大积分系数，适当减少比例和微分系数的作用［13］。由此建立输入输出的模糊规则表，见表1。

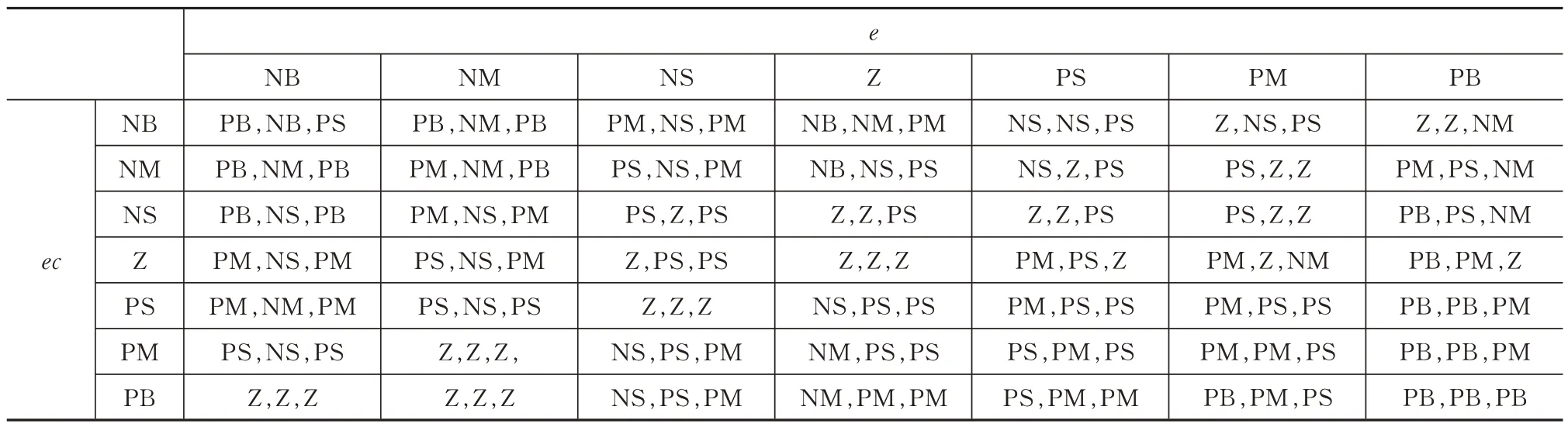
表1 模糊规则表Tab.1 Fuzzy rule table

由表1 以及隶属函数，可得到输出模糊子集的隶属度。解模糊的方法有最大隶属度法、重心法、加权平均法等。本文采用重心法进行反模糊化，使输出为具体值［14］，计算公式如下：

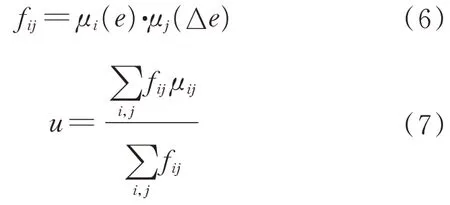
式中：μi(e)为系统误差e的隶属度；μj(Δe)为系统误差Δe的隶属度；fij为输出参数的隶属度；u为模糊控制器的输出；μij为所属的隶属模糊子集，其值由模糊规则表确定。

模糊输出参数公式如下：

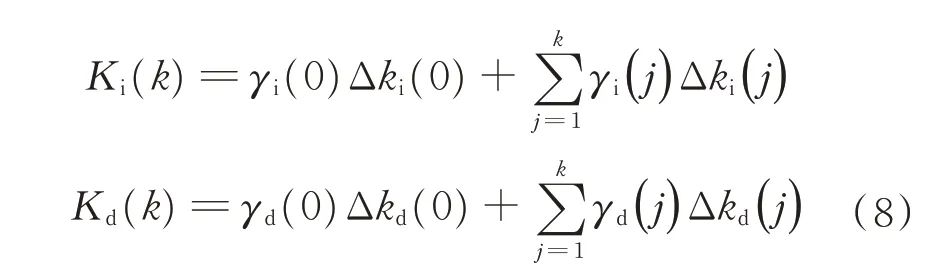
式中：Δkp（0）、Δki（0）、Δkd（0）为PID 控制参数初值；γp（j）、γi（j）、γd（j）为模糊输出的修正参数的比例系数；γp（0）、γi（0）、γd（0）为比例系数的初值。

2.3 单神经元控制算法

神经网络模拟是根据人脑的思维方式确定的数学模型，主要用于解决复杂的非线性、不确定系统。根据有监督的Hebb 学习规则，利用输入和输出调整神经元之间连接的权值，设计出自适应控制器［15］，其结构如图7 所示。

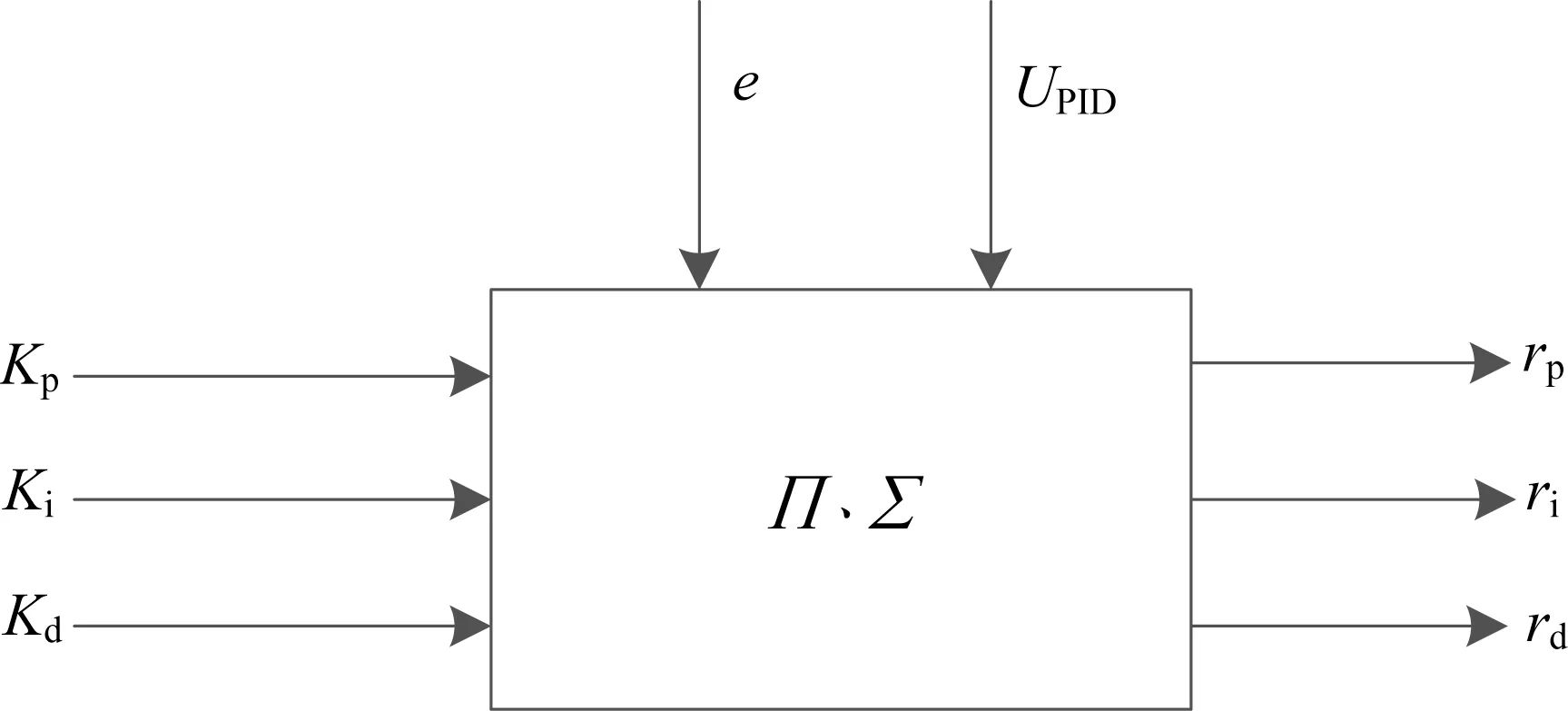
图7 单神经元结构图Fig.7 Diagram of single neuron structure

具体算法如下：

式中：ηp、ηi和ηd分别为比例P、积分I、微分D 的学习系数；UPID为PID 控制器的输出。其中，学习系数的制定一般按照经验选取。

3 仿真试验及结果分析

通过Matlab/Simulink 工具建立随动控制系统仿真模型，并加入模糊PID 控制、模糊单神经元PID控制进行仿真对比。对于发射车随动控制系统的参数，在实际调试过程中，一般运用斜坡信号、正弦信号进行调节［16］。为了验证模糊单神经元PID 算法的有效性，用函数信号发生器分别产生阶跃信号、正弦进行仿真验证。根据对车载随动系统的数学建模、模糊单神经元PID 控制器设计，可设计仿真结构如图8 所示。

图8 系统Simulink 仿真结构Fig.8 Simulation structure diagram of the system by Simulink

图8 中，Fuzzy Logic Controller为模糊逻辑控制器，Neuarl Controller为单神经元控制器，Derivative为微分环节，Transfer Fcn为辨识出来的传递函数。通过Switch 控件选择，分别实现模糊PID 控制与模糊单神经元PID 控制对传递函数的仿真，并对两者的输出结果进行对比。

在车载发射装置运动过程中，随动控制系统一般存在最优路径选择，即最大调转角度为180°。在仿真试验中，选取初值γp（j）、γi（j）、γd（j）为2.87、0.38、0.19。选取ηp、ηi和ηd学习系数分别为0.35、0.009、0.05。分别设置模拟输入幅值为90°、180°的阶跃信号，幅值为45°，周期为6.28 s 的正弦信号，并查看模糊PID 控制、模糊单神经元PID 控制的仿真结果，仿真结果如图9～图11 所示，其中，横坐标为时间，纵坐标为发射装置调转的角度。

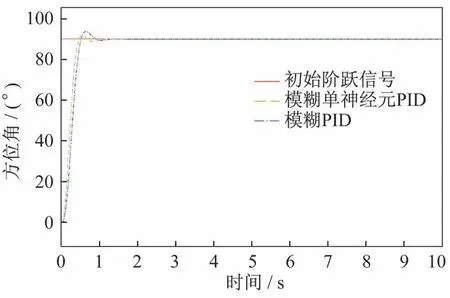
图9 幅值为90°的阶跃信号的仿真结果Fig.9 Simulation results of the step signal with amplitude of 90°

图10 幅值为180°的阶跃信号的仿真结果Fig.10 Simulation results of the step signal with amplitude of 180°

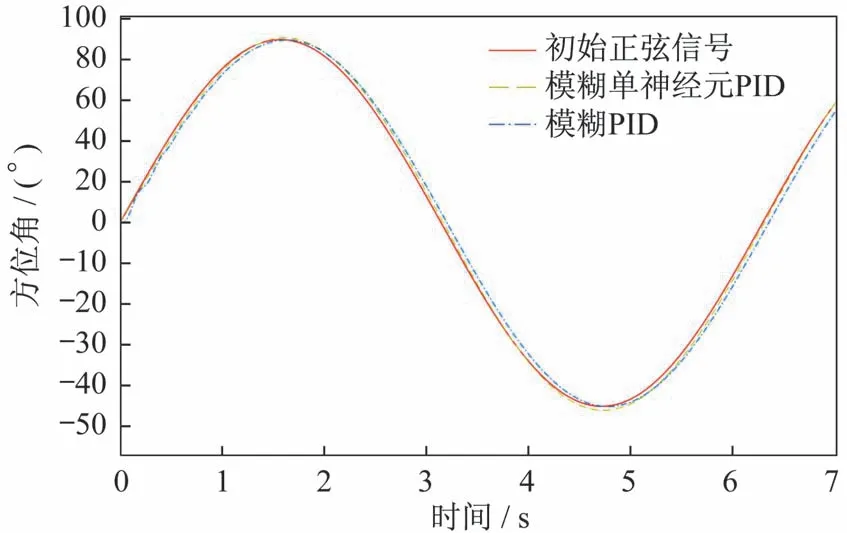
图11 幅值为45°、周期为6.28 s 的正弦信号的仿真结果Fig.11 Simulation results of the sinusoidal signal with amplitude of 45° and period of 6.28 s

通过分析对比2 个控制器的控制性能，整理结果见表2 和表3。

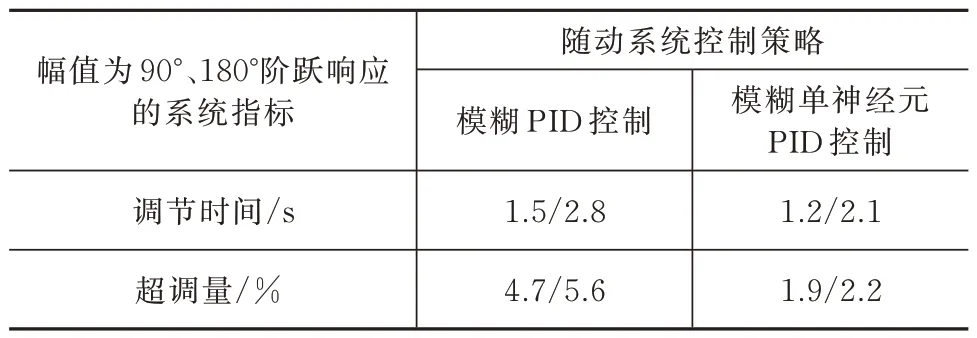
表2 幅值为90°、180°的阶跃信号的控制性能Tab.2 Control performance of the step signal with amplitude of 90° and 180°

表3 幅值为45°、周期为6.28 s 的正弦信号的控制性能Tab.3 Control performance of the sinusoidal signal with amplitude of 45° and period of 6.28 s

综合仿真结果和分析得出：对于阶跃信号，模糊单神经元PID 控制器相比传统模糊PID 控制器响应速度要快，且超调量明显缩小；对于正弦信号，模糊单神经元PID 控制的最大初始偏差角以及动态跟踪误差均优于模糊PID 控制。经过对传统模糊PID 控制的改进，模糊单神经元PID 控制器具有一定的学习能力和自适应能力，使得发射装置能够快速、准确、稳定地控制、执行随动控制指令，各项性能指标均达到系统作战要求。

4 结束语

本文对发射车随动系统的控制策略进行研究。首先，根据车载随动系统的组成及工作原理进行数学建模，并运用系统辨识及理论分析，得到车载随动系统的传递函数；其次，运用神经网络控制与模糊控制理论，以两种控制方法优缺点互补为思路，设计了单神经元模糊控制的学习规则，将单神经元与模糊PID 控制相结合的随动控制；最后，运用Matlab 中的Simulink 进行仿真。仿真结果表明，相比于传统模糊PID 控制，模糊单神经元PID 控制可以显著提高发射装置的静态、动态跟踪性能，验证了该随动控制策略的可行性。