中口径埋头弹火炮发射动力学建模及仿真

张世明，许管利，刘 丹，郭竞尧

(西北机电工程研究所，陕西 咸阳 712099)

1 引言

未来战争对火炮性能提出了更高要求，包括增大威力、减轻重量和提高射击精度，但是在传统武器框架下，平衡各项性能间的矛盾已几无余地，而埋头弹药武器系统的发展为此提供了一条可行途径。埋头弹药外形呈规则的圆柱体，长度相比传统弹药大大缩短；同时埋头弹火炮采用旋转闭锁新原理。基于以上两点原因，埋头弹火炮的总体尺寸大大减小，意味着可以在原有炮塔尺寸不变的前提下，换装较大口径的埋头弹火炮，从而有效提高武器系统的威力。武器系统的射击精度问题一直是国内外学者研究的热点，射击精度包括射击准确度和射击密集度，射击准确度可以通过调整弹道进行修正，而射击密集度需要从系统设计的各个环节加以控制[1]，因此研究射击密集度尤为重要，可以为火炮总体方案的论证和设计提供依据。

目前，对火炮射击密集度的研究方法主要有试验测试、多体动力学模拟和非线性有限元分析[2]。试验测试是检验火炮性能和诊断故障最直接的方法，但是需要在加工调试完成后才能进行[3]，无法在设计初期就进行核算验证，而且会耗费大量人力物力，而仿真技术的发展可以大大满足此类便捷性研究需求[4]。其中谢锋[5]通过对转管火炮的连发射击过程进行仿真分析，分析了炮口位移和速度对密集度的影响。刘威[6]采用ABAQUS建立火箭发射装置的有限元模型，分析单发射击时的炮口振动响应，进而估算火箭弹密集度偏差。方宇[7]建立了考虑悬挂的全炮动力学模型，分析了车载迫击炮的炮口振动特性。王丽群[8]采用神经网络对榴弹炮进行灵敏度分析，获得了各随机因素对射击密集度的影响规律。赵跃跃[9]建立了全炮刚柔耦合非线性有限元参数化模型，研究了结构参数对射击精度的影响规律。田发达[10]分析了不同发射工况下车载遥控武器站的炮口动力学特性。以上均以传统武器为对象进行研究分析，而埋头弹火炮采用新原理、新结构，与传统武器存在较大差异，目前对埋头弹火炮武器系统的发射动力学特性和射击精度问题还缺乏足够认识，无法为埋头弹火炮武器的设计与改进提供科学有效的指导。非线性有限元法运用离散概念，将弹性体拆分为多个有限元，单元经过联立求解出数值解。非线性有限元法充分考虑了火炮射击状态下零部件的弹性变形和非线性因素，如炮箱大位移滑动、零部件接触碰撞及火炮振动等，能够有效地反映火炮射击时的动态响应和力学特性。

本文中以中口径埋头弹火炮为研究对象，基于有限元理论建立火炮系统的非线性动力学模型，来研究其射击过程中的后坐特性和炮口动态响应，进而推算射击精度，并与射击试验测试数据进行对比分析，为埋头弹火炮的设计和研制提供参考。

2 理论基础

2.1 非线性动力学有限元理论

火炮作为一个非常复杂的系统，包含着许多零部件，零部件的弹性变形和刚体运动相互耦合，使得火炮发射表现为一种高瞬时、强冲击和高能量的非线性动力学过程[11]。这种非线性特性具体表现如下：

1)火炮系统内零部件之间存在间隙，射击时各部件之间通过接触碰撞来传递力和运动，零部件的受力与位移呈非线性关系；

2)火炮零部件之间发生较大相对位移时，运动规律随时间呈现出非线性变化。

不同的非线性特性相互交织，相辅相成，共同影响着火炮发射时的非线性动力学。非线性动态有限元能够全面地考虑这些非线性特性，从而相对真实地模拟发射过程中各部件的工作情况。

火炮射击时位移和外力都是时间的函数，根据达朗贝尔原理，可以引入惯性力将弹性体的动力学问题转化为静力学平衡问题。动态结构的非线性动力学有限元方程为：

(1)

其中：M为总体质量矩阵；C为总体阻尼矩阵；K为总体刚度矩阵；F为总体载荷矩阵。

t+Δt时刻的平衡方程为：

(2)

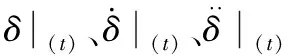
(3)

其中，α和β是积分参数。

令：

(4)

(5)

则：

(6)

令：

(7)

使用Newton-Raphson法对式(7)进行迭代，δ|(t)作为初始值，对节点位移当前值的参数进行Taylor展开，并设参数为0，得到：

(8)

忽略高于一阶的Δδ项，得到一个线性方程系统：

(9)

在获得节点位移的增量的基础上进行迭代，可得

δ(υ+1)=δ(υ)+Δδ

(10)

能量收敛准则：

|ΔδTr|=|Δδcrc|≤εmax(Wkin,Wint,Wext)

(11)

根据能量收敛准则进行迭代，直至满足条件为止。

2.2 炮口振动参数理论

中小口径武器通常为近距离直瞄射击，根据弹道学理论，在忽略横风和初速偏差等次要因素后，近距离立靶密集度的主要影响因素为跳角。跳角分为起始跳角和动力跳角，起始跳角主要由自重、加工误差和受热不对称等非振动因素导致的身管弯曲造成的，而动力跳角与射击载荷激发的炮口振动有关[12]。炮口振动会直接影响弹丸出炮口的姿态，从而影响射击精度。

以高低向回转中心为原点，沿炮膛轴线为x轴(指向炮口方向为正)，垂直炮膛轴线为y轴(向上为正)，建立炮弹半约束期运动模型如图1所示。

图1 炮弹半约束期模型示意图

高低跳角表示为：

φyi=αyi+βyi+δyi

(12)

(13)

(14)

式中：φyi为高低跳角；αyi为身管轴线与瞄准线在xoy面上投影的夹角，是由起落架运动导致的；βyi为炮口法线与炮膛轴线在xoy面上投影的夹角，是由身管弹性变形引起的；δyi为弹丸速度矢量与炮口法线在xoy面上投影的夹角，是由炮口振动引起的；yi为弹丸出炮口瞬间炮口中心点的高低向位移，Lg为炮口中心点到耳轴中心线的距离，vyi为弹丸出炮口瞬间弹丸初速在高低向的分量。

方向跳角表示为：

φzi=-αzi+βzi+δzi

(15)

(16)

(17)

式中：φzi为方向跳角；αzi为炮膛轴线与瞄准线在xoz面上投影的夹角；βzi为炮口法线与炮膛轴线在xoz面上投影的夹角；δzi为弹丸速度矢量与炮口法线在xoz面上投影的夹角；Zi为弹丸出炮口瞬间炮口中心点的方位向位移，Lf为炮口中心点到方位回转中心的距离，vzi为弹丸出炮口瞬间弹丸初速在方位向的分量。

结合式(12)～式(17)，射角为θ0时的立靶散布模型可表示为：

Δyi=Xtanφyi+yi

(18)

Δzi=Xtanφzi/cosθ0+zi

(19)

式中，X、θ0分别为立靶距离和初始射角。根据三角函数理论，在φ<5°时tanφ≈φ；且X/Lg和X/Lfcosθ0常大于100，炮口位移yi、zi对散布偏差的影响可以忽略。因此式(12)和(13)可简化为：

(20)

(21)

3 模型建立

3.1 基本假设

火炮射击时，各部件的受力情况比较复杂，属于多自由度运动。为了简化计算，在不影响虚拟样机合理性的前提下，对火炮射击时的运动和受力情况假设如下[13]：

1)火炮位于水平地面上，并且水平射击；

2)忽略小零件，将其质量添加到其他零件上；

3)火炮结构左右对称，射击时所有外力或其合力均位于火炮垂直对称面内。

3.2 虚拟样机

中口径埋头弹火炮由身管、炮箱、缓冲器、摇架和台架等零部件组成。后坐部分的质心和转动惯量对火炮的动态响应影响巨大，因此建模时这些参量应尽量与实际相一致；但是后坐部分结构复杂、零部件较多，在计算时会大大影响效率。通过对部分零件适当简化，将其质量添加到炮箱上，从而保证后坐部分质心和转动惯量不变。采用UG软件建立埋头弹火炮的三维模型，给模型中不同零件赋予相应的材料属性，其中身管和炮箱为高强度炮钢材料，摇架为铝合金，缓冲器和台架等部件为合金钢。将建立的模型导出为Parasolid类型，然后导入ABAQUS软件中，适时刚化部分零件。

主要使用六面体单元对实体进行网格划分，局部过渡区域采用四面体单元；对于板壳结构，采用壳单元来划分网格[14]。获得的火炮有限元模型含52 138个单元，59 862个节点，其中实体单元14 586个，壳单元37 551个，全炮的有限元模型如图2所示。

图2 有限元网格模型示意图

3.3 定义接触和施加载荷

身管后端嵌入炮箱中，直接对二者进行节点合并。炮箱和摇架通过缓冲器相连，其中缓冲器筒与摇架固定，缓冲器杆与炮箱固定，缓冲器筒和缓冲器杆通过缓冲簧形成接触关系。炮箱在重力作用下，与摇架上的导轨接触，导轨约束炮箱的运动；由于火炮后坐复进时炮箱和导轨之间存在大位移滑动，因此将其定义为有限滑移接触。摇架和托架之间通过耳轴铰接，采用Cartesion-Cardan复合连接器来模拟摇架和托架之间的转动关系，赋予5个自由度方向的刚度与阻尼，释放转动方向的刚度和阻尼。托架和机架之间通过螺栓连接，直接耦合螺栓位置处连接件之间的自由度。建立起全炮的拓扑关系如图3所示。

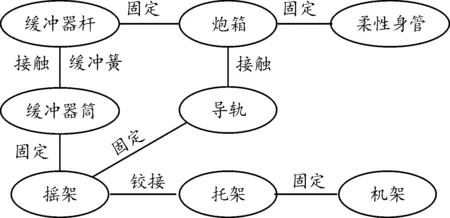
图3 系统拓扑关系框图

火炮射击时，主要受重力、炮膛合力、后坐阻力、支撑反力和导轨摩擦力的共同作用。火炮发射过程中的动载荷是由炮膛合力激发的；弹丸在膛内运动时期，炮膛合力通过膛压曲线计算求得，膛压载荷曲线如图4所示；在后效期内，随着火药气体从膛内高速喷出，膛内的气体密度和压力急剧下降，炮膛合力从弹丸出炮口瞬间的Fptg指数衰减为0，后效期炮膛合力的计算使用经验公式计算。炮膛合力[15]可以表示为：

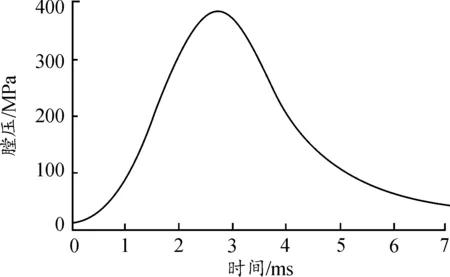
图4 膛压载荷曲线

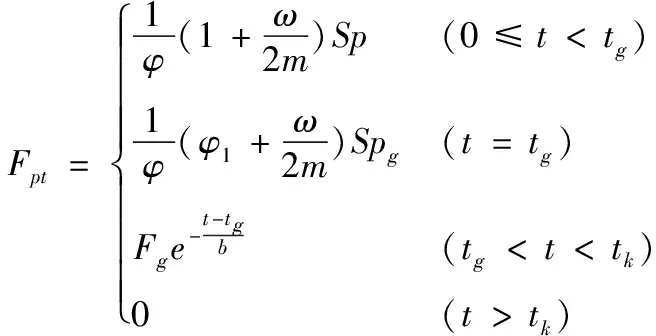
(22)

(23)

式中：ω为装药质量；m为弹丸质量；φ为次要功系数；φ1为弹丸在膛内运动阻力系数，一般取φ1≈1.02；S为炮膛横截面积；p为膛内平均压力；pg为弹丸脱离炮口时膛内的平均压力；b为反映炮膛合力衰减的时间参数；β为后效期作用系数tg为弹丸脱离炮口的时刻点；tk为膛内压力为0的时刻。

反后坐装置采用弹簧-液压式缓冲器，弹簧-液压式缓冲装置的弹簧为螺旋簧，自动炮后坐时弹簧缓冲储能，复进时弹簧释放能量，使自动炮复进到位；液压提供阻尼力，减小复进到位的速度。后坐阻力方程为[16]：

FR=Fφh+Ff+FT-mhgsinθ

(24)

(25)

(26)

式中：FR为后坐阻力；Fφh为后坐过程中的液压阻力；Ff为复进过程中的液压阻力；FT为摩擦力；mh为后坐质量；θ为俯仰角火炮射角；ρ为液体密度；K1为液压阻力系数；Asxh为后坐过程中活塞作用面积；Axh为后坐流液孔面积；Asxf为复进过程中活塞作用面积；Axf为复进流液孔面积。

f(Axh,Asxh)和f(Axf,Asxf)是缓冲器的结构参数，为定值；因此可知液压阻力与火炮运动速度的二次方成正比[17]。通过ABAQUS中的子程序提取炮箱运动速度，利用IF条件判断函数获得液压阻力：

IF(V∶-Ff, 0,Fφh)

(27)

4 动力学仿真分析

4.1 后坐特征分析

后坐阻力对火炮的后坐运动以及发射时的载荷传递有着重要影响，直接关系到火炮的射击精度。通过研究后坐阻力规律，有助于了解埋头弹火炮发射过程中的动力学特性，进而从降低火炮后坐阻力方面入手来提升火炮射击精度。

通过仿真分别获得后坐速度、后坐位移和后坐力随时间的变化曲线，并与试验测试结果进行对比，如图5～图7所示。前期在炮膛合力的作用下火炮快速后坐，后坐力迅速增大，炮膛合力在缓冲器的作用下得到有效释放。缓冲器的应用使得摇架受力大大降低，约为炮膛合力的几十分之一。在t=0.013 s时，炮膛合力和后坐阻力达到平衡，此时对应的最大后坐速度约为4 m/s。随着炮膛合力减小，后坐速度也相应减小，但后坐位移仍然增大，后坐力缓慢增长。当后坐速度降为0时，炮尾达到最大位移，随后火炮开始复进直至停稳，可以看出复进速度明显小于后坐速度。

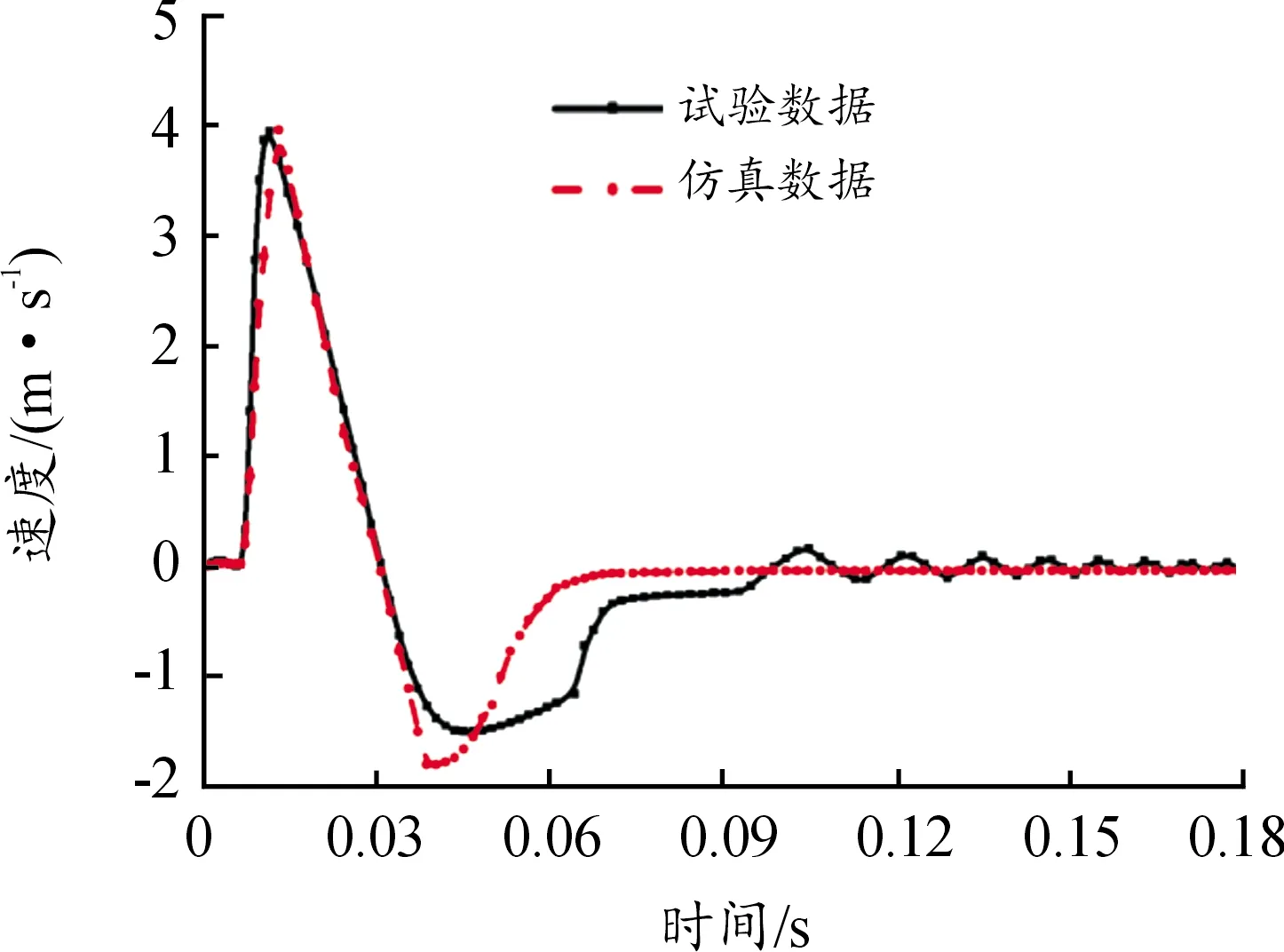
图5 后坐速度仿真与试验曲线

图6 后坐位移仿真与试验曲线

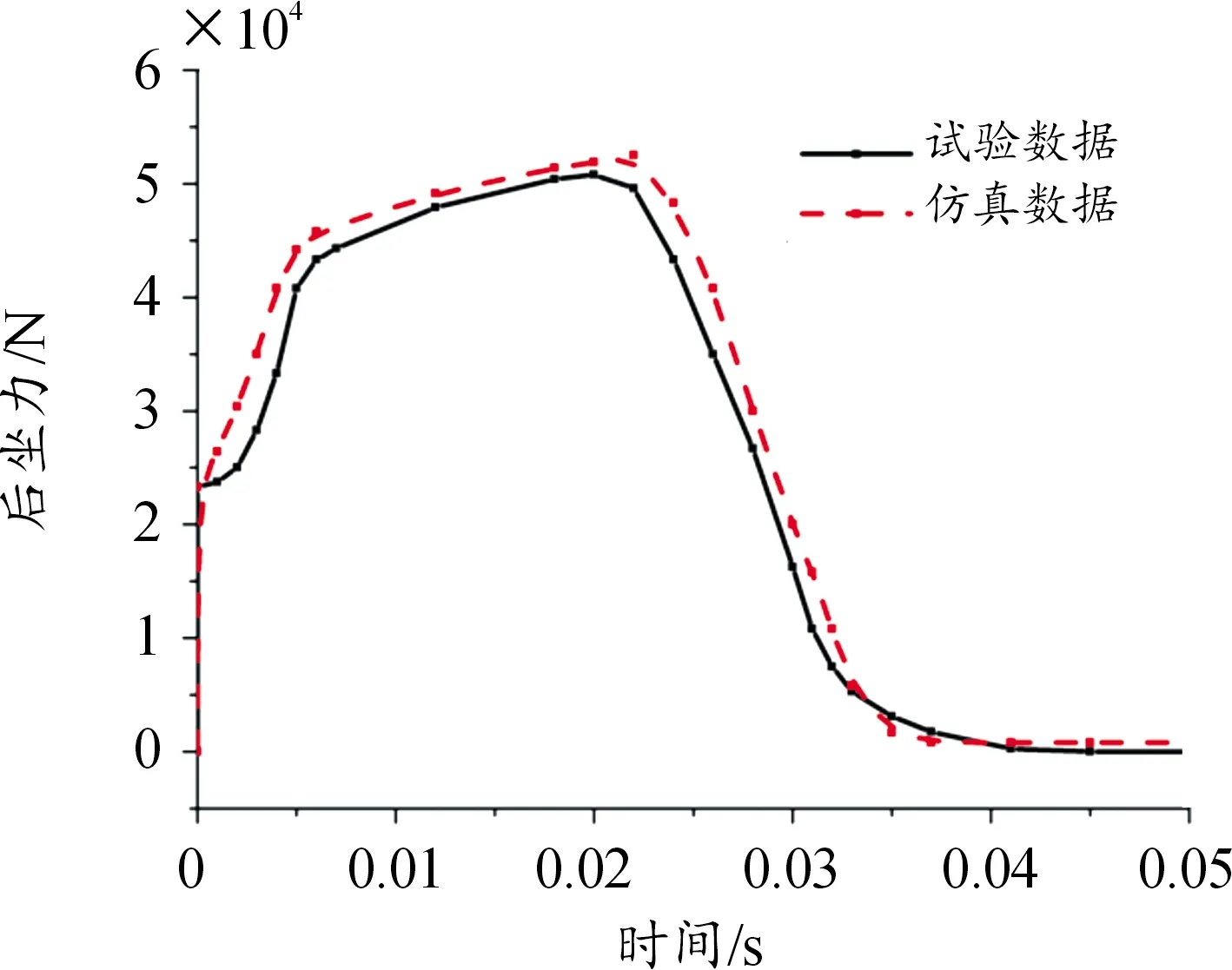
图7 后坐力仿真与试验曲线

通过仿真获得的最大后坐位移为45.5 mm，最大后坐力为52 500 N；试验测得的最大后坐力为51 000 N，最大后坐位移为44 mm。仿真结果与试验实测曲线重合度较高，误差在7%以内。误差出现的主要原因是仿真时火炮的模型有所简化，使得质量、转动惯量和质心位置存在差异。

4.2 炮口振动响应分析

炮口振动位移和线速度是影响火炮射击的主要分量，基于上述非线性有限元模型，获取射击过程中炮口的响应位移曲线如图8、图9所示，响应速度曲线如图10、图11所示。

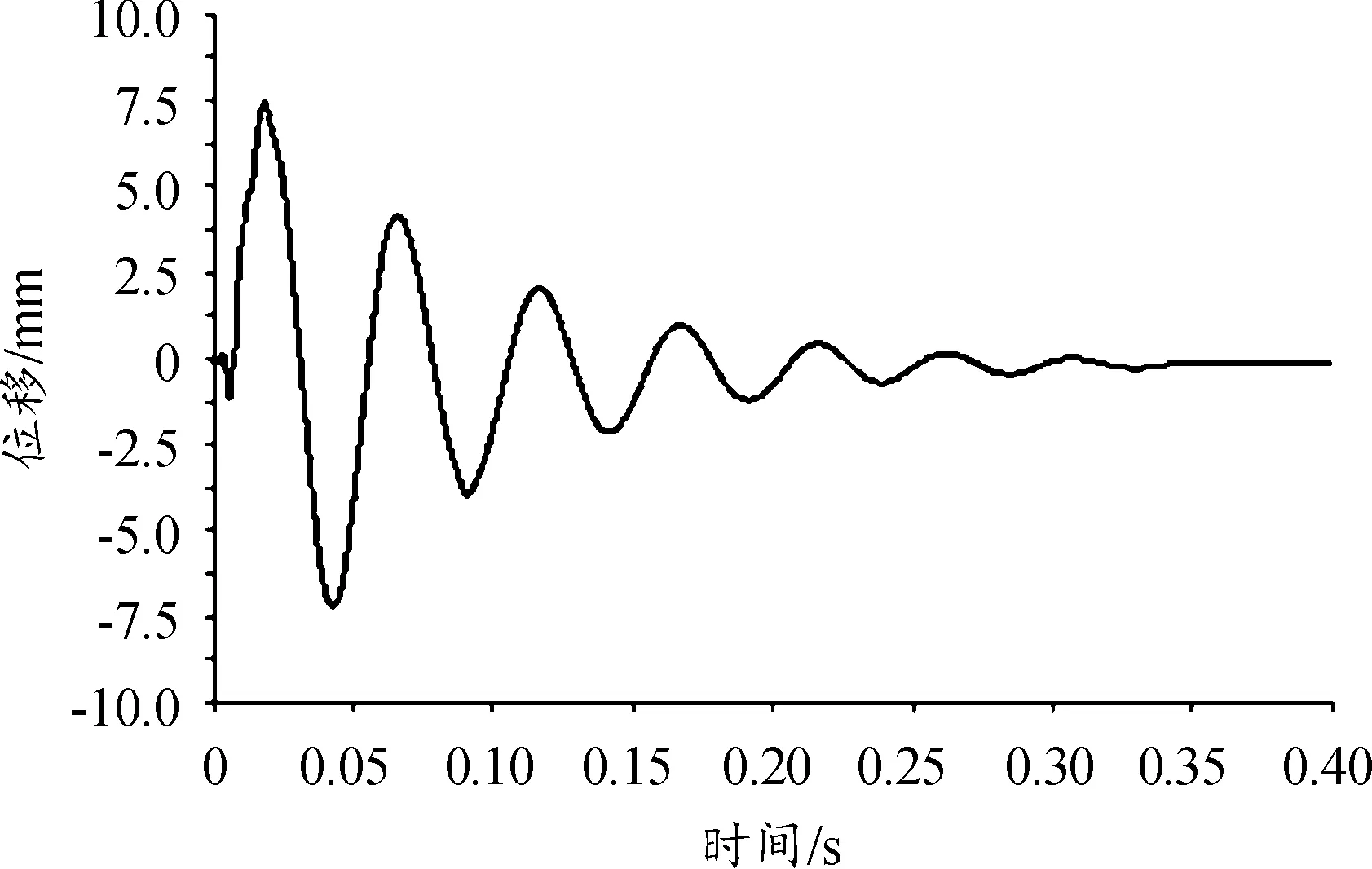
图8 炮口高低响应位移曲线

图9 炮口方位响应位移曲线

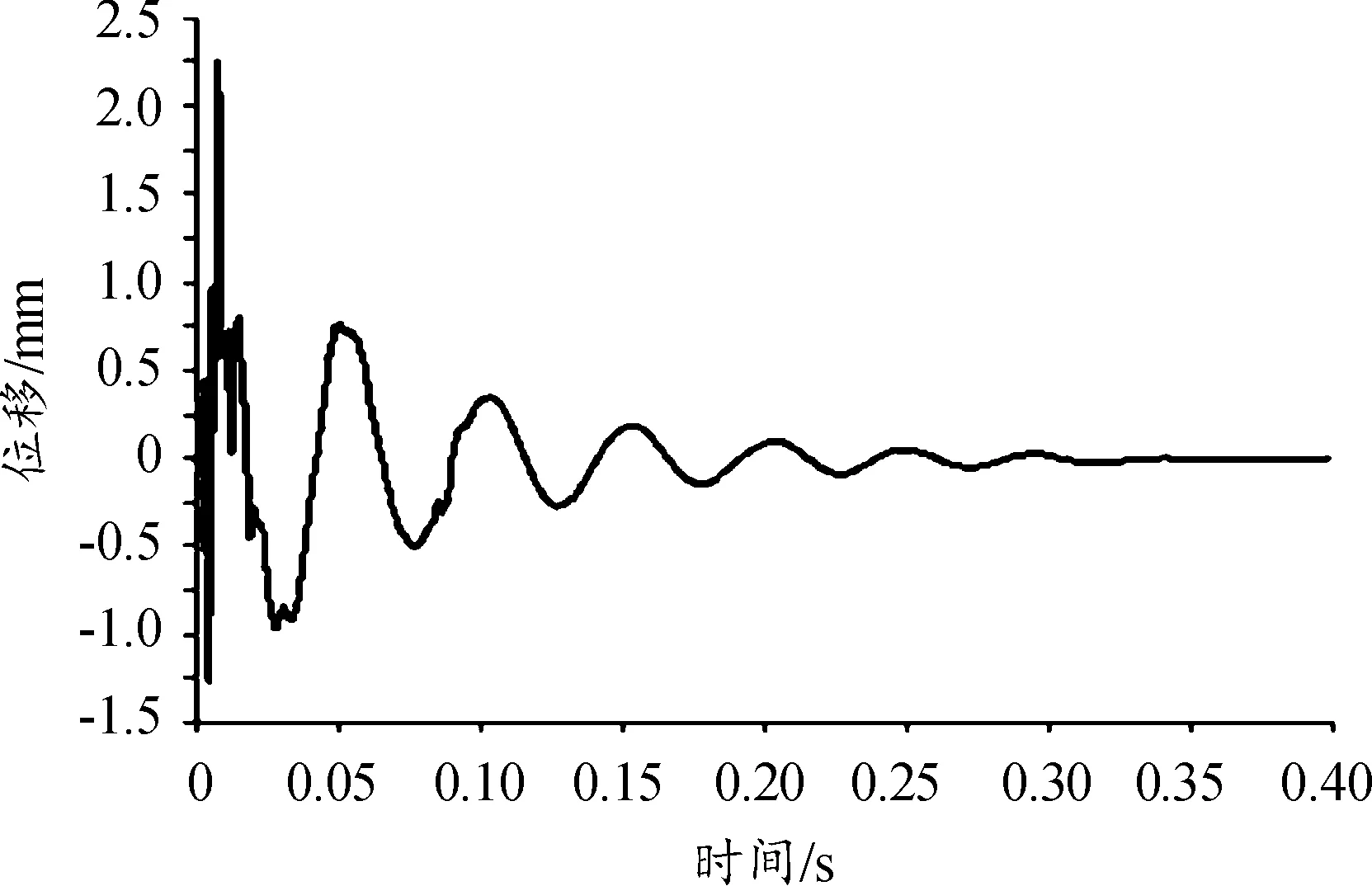
图10 炮口高低响应速度曲线

图11 炮口方位响应速度曲线

仿真结果表明，在炮膛合力作用前期，炮口位移和速度变化幅度不大。在炮膛合力作用后期，炮口振动速度迅速增大；其中炮口高低向振动最大速度为2.25 m/s，在0.022 s时高低向位移达到最大7.48 mm，持续振动约0.34 s后趋于平稳；方位向振动最大速度为0.38 m/s，在0.075 s时方位向位移达到最大0.95 mm，持续振动约0.45 s后趋于平稳。

弹丸飞出炮口后，后续炮口振动不会继续干扰弹丸飞出炮口时的姿态，也就不会影响射击精度，因此弹丸飞出炮口时的炮口振动响应是影响射击精度的主要因素。已知弹药内弹道时间为0.009 s，根据弹丸出炮口的时间计算出此刻炮口高低位移为0.98 mm(向上)、方位位移为0.51 mm(向右)。立靶距离110 m，弹丸初速为890 m/s，将炮口振动的位移值代入外弹道计算软件中获得立靶坐标值，进而求得高低方向密集度为0.72 mil，方位方向密集度为0.44 mil。

4.3 验证

为了验证炮口响应仿真结果的有效性，对火炮样机进行单发射击试验，其中靶板距离样机110 m，经过瞄准校靶后进行试验。对初速偏差较大及射击时超过允许风速的弹丸着靶数据点剔除，获得射击数据如表1所示。

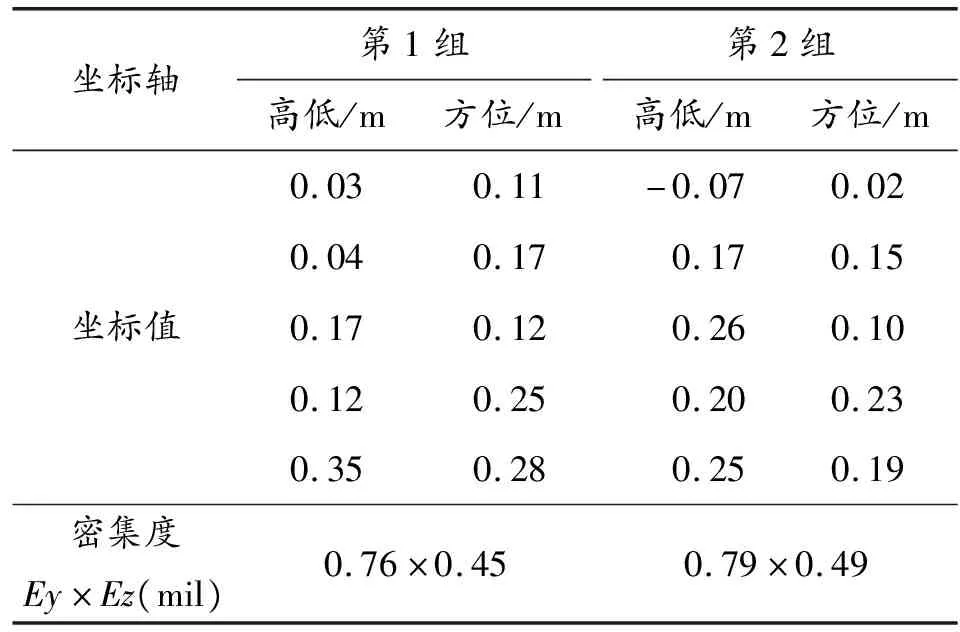
表1 密集度试验结果

通过对弹丸着靶点位置的测量，分别计算出高低和方位密集度，其中高低方向密集度平均为0.775 mil，水平方向密集度平均为0.47 mil。以射击试验获得的立靶密集度数据为基础，计算仿真立靶密集度相对于试验立靶密集度的误差，高低方向密集度误差为7.6%，方位方向密集度误差为6.8%。

5 结论

本文建立了中口径埋头弹火炮系统的非线性动力学有限元模型，通过仿真分别获得了后坐特征和炮口动态响应曲线。获得的仿真分析结果和测试数据较为吻合，验证了模型的有效性和正确性。炮口响应高低方向密集度误差小于7.6%，方位方向密集度误差小于6.8%，说明建立的仿真模型能够满足工程设计需求，可以为中口径埋头弹火炮系统结构设计及优化提供参考。