从波动光学角度解析彩虹

贾嘉琪，黄 振，许清滢，吴青林

(华中师范大学 物理科学与技术学院,湖北 武汉 430079)

波动光学以光的电磁理论为基础研究光的传播规律.相比于几何光学，波动光学的物理模型和所得计算结果更加直观，理论上所有用几何光学解释的光学现象都可以用波动光学来解释.在传统的光学教学中，为了照顾学生的认知水平，彩虹现象的探究大多放在几何光学部分，运用费马原理推导出彩虹角[1]来解释彩虹现象，但除彩虹角以外的许多现象单单使用几何光学是无法解释的.在电磁学课程中，学生学习了电磁波理论、能流密度、电磁波在电介质界面的边界条件等知识，应用电磁场的边界条件推导出的菲涅耳公式可以定量计算反射和折射光强.因而本文从光的电磁理论[2]出发，对彩虹的形成机制给出解释，以弥补用几何光学探究其现象时的不足之处.

1 彩虹角的几何光学解释

早在1637年笛卡尔就指出，彩虹是太阳光经过空气中的水滴折射-反射-折射后形成的[3]，如图1所示，1为入射光线，3为折射后进入人眼的光线.D为折射光线相对于入射光线的偏转角，入射光线和折射光线的夹角φ就是地面上的人所看到的彩虹的视场角.彩虹一般出现在清晨或傍晚时分雨后天晴的天空，地面观察者看到的彩虹的视场角约为42°. 根据几何光学中光的反射和折射定律并结合费马原理可以计算出这个角度.

图1 彩虹光路示意图

由费马原理可知，实际光线对应的光程总是取平稳值.对于图1所示的彩虹的光路图，光程取平稳值等效于偏转角D或视场角φ取平稳值.雨后天空形成彩虹的水滴尺寸约为毫米量级，可看作是理想的球形，由平面几何知识可得空气水滴界面的入射角、反射角和折射角与偏转角D或视角φ的关系，如图1所示.设入射光的波长为λ，水滴的折射率为n，可得偏转角D、视角φ随入射角θ1之间的关系为

(1)

由式(1)可知φ与折射率n有关，太阳光可看作是由不同波长的复色光组成的，水滴对不同波长光的折射率及对应的视场角如表1所示.

折射率n给定时，视角φ是入射角θ1的连续函数，如图2所示，φ随入射角θ1先增后减，在42°附近达到最大值，这就是由费马原理求解的彩虹角.由图2可以定性的解释为何人眼看到的彩虹角是42°.

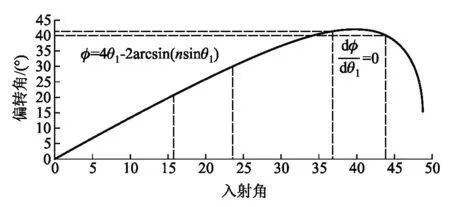
图2 视场角φ随入射角θ1变化曲线

在彩虹形成过程中，可以认为入射的太阳光是平行光线，通过Matlab[4]模拟多条平行光线入射，对同一偏转角的出射光线计数，分析各个偏转角处的光强.如图3所示，在偏转角42～43°能量最为集中，与费马原理得出的结论相符.但是根据几何光学和费马原理无法定量计算出光强.为给出光强的具体数值，需要从波动光学入手，应用菲涅耳公式进行定量计算.

图3 Matlab模拟入射光

2 彩虹角的波动光学解释

在光学课程中，应用电磁场的边界条件推导出菲涅耳公式，可以定量计算反射和折射光强.如图4所示，应用菲涅耳公式计算出射光的振幅与入射角的关系.

图4 主虹光路图

1)E⊥于入射面

(2)

(3)

(4)

联立式(1)～(3), 可得

(5)

2)E∥于入射面

(6)

(7)

(8)

联立式(5)～(7), 可得

(9)

2.1 主虹的视场角——彩虹角

通过代入红橙黄绿蓝靛紫七种颜色的光在水中的折射率，并利用计算机进行定量计算，可以得到各种频率的出射光s分量与p分量光强随偏转角的变化.

图5 主虹出射光s分量光强随偏转角变化曲线图

图6 主虹出射光p 分量光强随偏转角变化曲线图

将s分量和p分量相加即得总光强，出射光总光强随偏转角变化如图7所示，由图7可以看出光强几乎都集中在最大偏转角附近，无论是何种颜色的光，出射光的最大光强对应的偏转角都在40～42°区间中.如表2所示，各个波段出射光的光强最大值所对应角度不同，随着光波长的增加，最大光强所对应的偏转角也会增加，且运用波动光学计算得到的彩虹角与几何光学结果相同.

图7 主虹出射光总光强随偏转角变化曲线图

2.2 主虹颜色排列顺序

依据表2将红光与紫光的光路单独画出，得到图8，可以看出白光经过小水珠两次折射一次反射形成了一个40～42°上紫下红的彩色光锥.而人眼看到的彩虹颜色的顺序却是上下颠倒的，这是由于人眼的入瞳很小，可以近似将人眼看做一个点，每一个彩色光锥发出的光在人眼中成像需要满足：入射光经过水珠的偏转角=人眼与水滴的连线和入射光的夹角.如图9(a)所示，在任一平面内，上方水珠出射的红光进入人眼，下方水珠出射的紫光进入人眼，因此人眼所见彩虹的颜色由上至下为红橙黄绿蓝靛紫.如图9(b)所示[5]，太阳光入射到弥漫了小水珠的环境中，对人眼而言就在视场角为40～42°的范围内看到彩虹.

表2 主虹各波段出射光的偏转角和相对光强

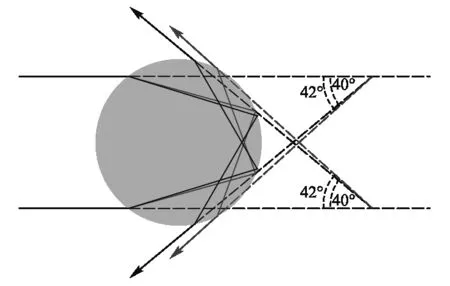
图8 白光经过小水珠两次折射一次反射

图9 彩虹在人眼中成像的示意图

人在地面上时，只有空中的小水珠折射光线，所以看到的都是半弧状的彩虹.当人在飞机或高山上观察时，人的水平线以下也有小水珠折射光线进入人眼，此时就可以看到完整的圆环状彩虹了.如图10所示[6].

图10 高空中看到的圆环状的彩虹

2.3 副虹

副虹也称霓，位于主虹的外侧，光路图如图11所示，其形成的原因和主虹相同，只是光线在水珠中的反射比形成主虹时多一次，同样可以运用几何光学和波动光学分析其原理与特征.副虹的几何光学计算方法与主虹相同.利用电磁场边界条件与菲涅耳公式，用计算机模拟得到各频率的出射光s分量和p分量的光强随偏转角的变化，如图12所示，两者相加即出射光总光强随偏转角的变化，如图14所示.

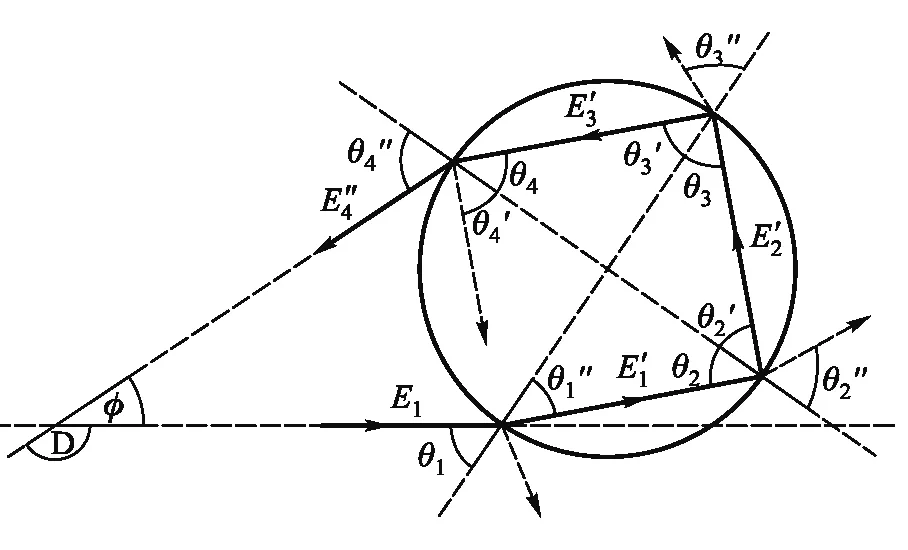
图11 副虹光路图

图12 副虹出射光s分量光强随偏转角变化曲线图

图13 副虹出射光p分量光强随偏转角变化曲线图

图14 副虹出射光总光强随偏转角变化曲线图

如表3所示，几何光学与波动光学的计算所得的副虹彩虹角相同，通过对比主虹与副虹的偏转角不难发现：主虹紫光的偏转角最大，而副虹与之相反.故结合上文介绍的彩色环带排序原理可知，副虹为内红外紫，与主虹排序相反.观察图10可以发现，此结论与生活实际观察现象相符.

表3 主副虹各波段出射光的偏转角和相对光强

2.4 彩虹各部分亮度分布

由上述计算结果可以看出主虹、副虹以及内外侧的光强分布是不均匀的，以黄色光为例，主虹最大光强为7.379 6，副虹的最大光强为1.948 5，仅为主虹的26.4%，所以副虹的亮度比主虹小得多.主虹内侧光强为4.477 6，副虹外侧为1.977 0，比主虹内侧更暗.主虹和副虹之间光强为零，所以最暗，称为Alexander 暗带.

可以看出，副虹出射光在52°左右相对光强最大，是55～65°之间的光强的9～20倍.且副虹的最大光强仅为主虹最大光强的24.3～33.1%，所以副虹的亮度比主虹要小得多.

2.5 彩虹是偏振光

3 总结

本文阐述了几何光学解释彩虹角的过程，并为了对彩虹现象的原理与特征给予更加全面和准确的解释，从波动光学出发，应用菲涅耳公式定量计算了出射光强与偏转角的关系,得到了与几何光学结果高度吻合的彩虹角，从而给出彩虹角更加直观的理论解释.同时运用出射光的光强结果定量地对比了主虹与副虹的光强大小，解释了彩虹光的高度偏振现象.