关于量子力学原理的注记
杨师杰
(北京师范大学 物理学系,北京 100875)
在经典力学中,质点的状态由位置和动量(速度)(q,p)完整地描述,这样一对物理量被称作正则共轭量,它满足哈密顿运动方程:
(1)
其中j=1,2,…,n代表n维空间独立坐标.对于N质点系统,由独立变量(q,p)张开一个2nN维的相空间,相空间中的一点代表质点系的一个完整状态,质点系的时间演化即为相空间里的一条轨迹.对于孤立系统,这条轨迹被约束在相空间中的等能面上.
量子力学的情况有所不同,由于位置和动量不是好物理量,不能用它们来描述微观粒子的状态.我们设想仍然存在一个状态量|ψ〉,它完备地描述粒子的全部物理性质,那么需要解决下面几个问题:1) 状态量|ψ〉处于什么样的空间中?2) 状态量|ψ〉具有什么基本特性?3) 状态量|ψ〉在该空间中随时间如何演化?相对于经典力学的相空间,量子系统所有可能的状态集合构成一个完备的复内积空间,冯·诺依曼称之为希尔伯特空间[1].所以状态量|ψ〉是希尔伯特空间中的一个向量,它满足线性叠加原理,并且保持归一化条件:〈ψ|ψ〉≡1. 所有力学量都被视作对量子态进行线性变换操作的算符,该操作不会导致状态量超出原来的希尔伯特空间,为此要求力学量都是自伴算符.
为了得到状态量|ψ(t)〉随时间演化的动力学方程,引入演化算符U(t,t0),有
|ψ(t)〉=U(t,t0)|ψ(t0)〉
(2)
其中|ψ(t0)〉是t0时刻的状态量.由于〈ψ(t)|ψ(t)〉=〈ψ(t0)|ψ(t0)〉=1,可知
U†(t,t0)U(t,t0)=1
(3)
即U(t,t0)必须是幺正算符,可表示为U(t,t0)=eiΛ(t,t0),其中Λ=Λ†为厄米算符.现在考虑一个具有时间平移不变的系统,状态量|ψ(t)〉应该具有什么形式呢?如果系统处于能量本征态,由于形式上状态没有任何改变,极有可能的情形是
|ψ(t)〉~e-iα(t-t0)|ψ(t0)〉
其中α是常量.经典力学中具有时间平移不变的系统必定能量守恒,所以常量α可能与系统的能量E有关.考虑到状态向量的线性叠加原理——不同状态可能具有不同的能量——常量α应该与系统的哈密顿量H有关.我们可以合理地猜测状态演化的一般式为 |ψ(t)〉=e-iH(t-t0)/ћ|ψ(t0)〉
(4)
普朗克常量ћ的出现是出于消除量纲的需要,这个常量出现得多么及时!没有这个常量,时间平移的态演化幺正性假设就不能成立.如果哈密顿量含时,则一般的态演化方程应为
(5)
否则将导致关于时间的非线性演化.
如果上述猜测是正确的,那么很容易得到状态量|ψ(t)〉满足的动力学方程为

(6)
这就是薛定谔方程.至此,我们尚不知道哈密顿量H以及其他力学量算符具有何种形式.值得注意的是,该方程与哈密顿量的具体形式无关,它既适用于中心力场这类有经典对应的力学系统,也适用于自旋这类没有经典对应的纯量子系统,尤其是,它对于非相对论情形和相对论情形都同样适用!
(7)

(8)
哈密顿算符的矩阵表示为
态演化方程(6)可写成


所以系数的演化由矩阵方程描述:

(9)
下面讨论表象及表象变换理论.以一维为例,位置算符x的本征方程为x|x〉=x|x〉


由位置基向量表示的空间称作坐标表象.坐标表象下的量子态表示为
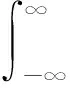
(10)
投影ψ(x,t)就是通常的波函数.由归一化条件〈ψ(t)|ψ(t)〉=1,可知

哥本哈根学派将|ψ(x,t)|2解释为粒子在位置x出现的概率密度.
假设还存在另一个具有连续谱的算符p,其本征向量为|p〉:
p|p〉=p|p〉


根据δ函数的性质:



(11)
如果将p视作动量,由于px具有作用量的量纲[J·s],普朗克常量ћ再一次及时出现,指数相因子应该除去ћ,即
(12)

(13)
它与坐标表象的波函数ψ(x,t)之间恰好构成傅里叶变换!根据傅里叶变换的标度性定理可知,函数在位形空间的分布宽度与其在动量空间的分布宽度成反比ΔxΔk~1,即
ΔxΔp~ћ
(14)
所以被视作量子力学核心的不确定性原理,其实是表象变换蕴含的必然结果,它与量子态的演化动力学没有内在逻辑关系.需要特别指出的是,普朗克常量ћ可视作量子系统作表象变换的不变量,如同光速c被视作力学系统作洛伦兹变换的不变量,以及电荷e被视作电磁系统作规范变换的不变量.
将动量算符p作用在位置基向量上,有




-iћ〈x′|x〉+x〈x′|p|x〉,
〈x′|xp|x〉=x′〈x′|p|x〉
→〈x′|xp-px|x〉=iћ〈x′|x〉
表明算符x和p的泊松括号具有常数谱,所以它们满足正则对易关系:
[x,p]=iћ
(15)
坐标表象下的哈密顿算符为
态向量的演化方程表示为


即
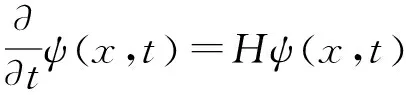
(16)
这就是坐标表象下的薛定谔波动方程.
在量子力学中,所有的物理可观测量都是希尔伯特空间中的自伴算符,A=A†.物理量的实验测量值就是力学量算符在量子态下的平均值:
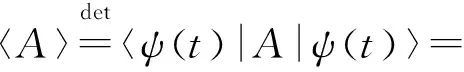


(17)
至此,我们已经演绎了量子力学的基本框架.现在还剩下一项任务,那就是验证薛定谔方程的合法性.我们要求由它得到的结果在ћ→0时,能够无缝地过渡到经典力学.在经典力学中,力学量随时间的演化满足哈密顿运动方程:
(18)
其中{,}表示经典泊松括号.当力学量算符不含时,其态平均值随时间的演化方程为
(19)

(20)
可见力学量的量子运动方程和经典运动方程在逻辑上是一致的.
梳理一下量子力学理论的脉络,有以下两条基本原理或假设:
1) 粒子的状态由希尔伯特空间的归一化态向量完备地描述,所有力学量都是作用于该空间的自伴算符;
2) 存在普朗克常量ћ,量子态随时间的演化由|ψ(t)〉=e-iH(t-t0)/ћ|ψ(t0)〉决定,其中H是描述粒子的哈密顿量.
这两条假设中的第1条是数学公理,第2条才是物理公理.量子力学理论的其他假设都可归结于对数学概念与可观测量之间关系的物理解释.
我们再讨论量子力学的路径积分表示.费曼考虑粒子从A出发的粒子经过所有路径达到B的概率幅,他假设每条路径贡献一个与作用量成正比的相位[3]:
其中S[x(t)]为沿任意路径x(t)的作用量.费曼基于此假设推导出薛定谔波动方程及整个路径积分框架.我们现在从量子态的一般演化式(5)出发推演量子力学的路径积分理论.将t0到t的时间等分为N段,tk=kΔt(k=1,2,…,N-1),有
U(tB,tA)=
U(tB,tN-1)U(tN-1,tN-2)…U(tk,tk-1)…U(t1,tA)
则
K(B,A)=〈xB|U(t,t0)|xA〉=
〈xB|U(tB,tN-1)|xN-1〉〈xN-1|…
|xk+1〉〈xk+1|U(tk+1,tk)|xk〉…〈x1|U(t1,t0)|xA〉
当N→∞,Δt→0时,取一阶近似
有
〈xk+1|U(tk+1,tk)|xk〉=
(21)
K(B,A)=

(22)


图1 路径积分
(23)
粒子传播到B点的总概率幅是将所有可能时序路径的概率幅叠加起来,用符号D[x(t)]表示为
(24)
这样就得到了费曼的假设式(21),注意此处丢弃了一个异常无穷大的归一化因子(N→∞,Δt→0).在推导式(24)时,我们利用了高斯积分,它源于哈密顿量中能量与动量成二次函数关系,非此则传播子表示为相空间的路径积分形式[4]
(25)
假设宏观粒子的经典路径为xcl(t),令S[x(t)]=S[xcl(t)]+δS[x(t)],由于ћ很小,偏离经典路径的相位δS[x(t)]/ћ导致概率幅急剧振荡,不同路径对概率幅贡献互相抵消,所以经典路径满足δS[x(t)]=0,即作用量S[x(t)]取极值的情形,这被称作最小作用量原理.
(26)
可得相干态路径积分的拉格朗日量为
(27)
对于量子自旋系统的路径积分表示,相干态之间的内积会导致一个几何相位,通常称作贝里相,它不是由哈密顿量决定,但可以影响系统的动力学行为.比如自旋-1/2系统H=B·S,取相干态|n〉=|z〉,采用旋量表示:
(28)
其传播子为[5]
(29)
其中
(30)

S[n(t)]=-∮BnSdt+
(31)
其中D是闭合路径对应的球面区域.
路径积分方法对于讨论多粒子相互作用的系统显示出极强的实用性,它将不同自由粒子及其相互作用的作用量简单地加起来即可
Stot=Sfree+Sint+…
(32)
这种形式十分便利于发展量子场和有限温度量子统计理论.考虑单粒子配分函数的路径积分表示:
(33)
其中β=1/T是温度的倒数,其中K(xB,xA,β)≡〈xB|e-βH|xA〉可视做沿着虚时的传播函数,按照相似的推导,可得相空间的路径积分:
K(xB,xA,τ)=
(34)
于是配分函数为
(35)
其中x(0)=x(β),p(0)=p(β),即可以把虚时方向看作是闭合的,通过解析延拓可化为实时传播函数
K(xB,xA,τ)|τ=it=iK(xB,xA,t)
(36)
致谢:作者感谢郭文安教授的许多讨论和评论.
——卡文迪什测定万有引力常量

