具有能量子库的活性布朗粒子的动力学研究

邱 星，杨紫贝，夏诗琪，王海燕

(北京师范大学 物理学系，北京 100875)

布朗运动自发现以来被很多科学家深入研究，布朗运动的理论在物理、化学甚至经济领域得到了广泛的应用[1-3]．但生物体中的主动运动，比如分子马达在轨道上的定向运动，细胞的迁移和微生物的定向运动等，这些运动主体可以吸收能量，使系统远离热平衡状态[4-6]，基于热涨落的布朗运动理论(本文称之为被动布朗运动理论)很难解释这些现象．因此，为了揭示生物体中主动输运的物理机制，研究人员提出具有能量子库的活性布朗粒子模型[7-12]．研究表明，具有能量子库的活性布朗粒子模型不但可以解释生物体内定向运动的物理机制，而且可以加深人们对非平衡统计物理的理解.

活性布朗粒子模型最初由德国洪堡大学Werner Ebeling团队提出[10,11]，其重要特性就是摩擦系数是粒子速度的非线性函数，发现活性布朗粒子从环境中吸收能量，储存于能量子库，并能够将能量转化为定向运动．Yu. M. Romanovsky等进一步研究了内部振子与能量子库耦合的活性布朗马达模型，并将该模型应用于转动马达的研究中[8]．A. Fiasconaro等研究了非对称棘轮势中的活性布朗粒子在泊松噪声驱动下运动的定向性和能量转化效率对随机能量关联时间的依赖关系[9]． 浙江大学邓茂林[13-15]等学者从理论上研究了活性布朗粒子的动力学，得到在抛物型势能和高斯白噪声驱动下的稳态解析解，发现在四维相空间上，系统处于远离平衡态时的扩散极限环．由于活性布朗粒子能够从环境中吸收能量，活性布朗粒子系统远离热力学平衡状态，呈现出复杂的动力学行为和反常扩散特征,还存在很多富有挑战性的问题[16].

本文基于德国洪堡大学Werner Ebeling研究小组提出的活性布朗粒子模型[10，11]，分析了内部能源子库的活性布朗粒子模型的阻尼特性，通过与被动布朗粒子比较，分别在自由场、谐振子势和非对称周期势中利用了Matlab软件模拟活性布朗粒子的随机动力学行为，发现非对称周期势垒的高度是活性布朗粒子定向运动的关键因素之一．本研究可以为统计物理教学提供一个有趣的实例，同时为大学生利用物理规律解决实际问题提供可以借鉴的思路和方法.

1 模型与方法

1.1 活性布朗粒子模型

为研究微小生物体的运动特性，本文不考虑微小的生物体内部结构，把微小的生物体抽象为具有内部能源子库的布朗粒子．内部能源子库总能量用e(t)表示，q(r)是单位时间在r处流入库的能量，内部能源库的平衡方程可以表示为

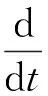
(1)

其中，c是生物体内部损耗系数，代表了生物体内部能量损耗；d(v)是能量转化为动能的比率，可以表达为

d(v)=d2v2

(2)

d2是转换系数，且d2≥0．v是粒子运动速度．考虑整个系统的能量，E0是系统的机械能，系统机械能平衡方程:

(3)

其中，γ0是阻尼系数，U(r)是势能函数，E0(t)是系统的机械能．在系统中，机械能的变化来自两个方面：能量子库输入的能量：d2ev2；由于摩擦损耗的能量：γ0v2．考虑随机力的影响，活性布朗粒子的运动方程为

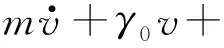
(4)

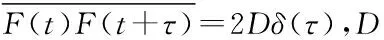
D=kTγ0

(5)

k是玻耳兹曼常数，T是环境温度．与描述被动布朗粒子的郎之万方程相比，式(4)增加了一项d2ev，这一项表明内部能源库在速度v方向上提供了加速度．通过把速度v的系数合并，我们重新定义摩擦系数γ(v):

γ(v)=γ0-d2e(t)

(6)

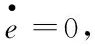
(7)

在平衡时，子库的能量e0是流入能量通量和系统损耗能量的系数的比值，损耗主要来自系统内部损耗和输出转化为动能．将式(7)带入式(6)，我们得到准静态过程中的摩擦系数与粒子速度的关系，如图1 所示.

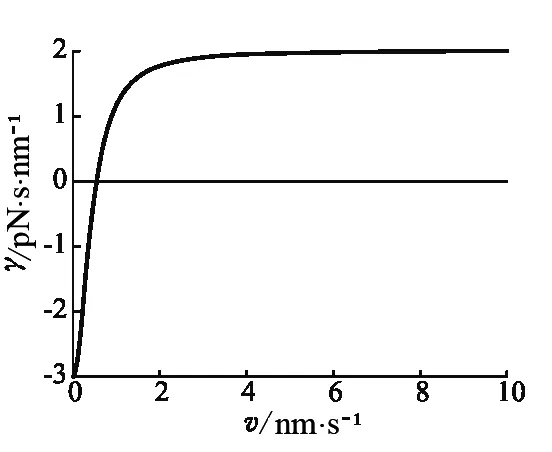
图1 摩擦系数和速度(γ0=2.0,c=0.2,q0=1.0,d2=1.0)

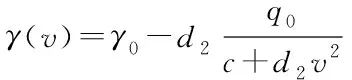
(8)

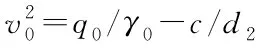
1.2 模拟方法

本文采用的数值解法是改进-欧拉法，又称预估-修正算法:

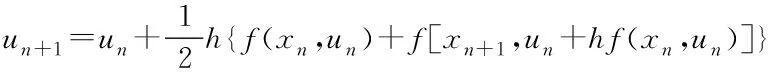
(9)

un表示函数在运算进行n步时的函数值，h是每一步的步长，xn是运算进行到第n步时自变量的值，f(xn,un)是un对xn的导数．欧拉法的思想是函数在n+1步的值由第n步的值和第n步函数的微分决定，预估-修正算法则通过计算第n步的导数，得到欧拉法中un+1的值，再计算出n+1的导数f[xn+1,un+hf(xn,un)]，两个导数的平均值才是第n步计算需要的导数值，这种方法的优势是可以提高计算的精度.

在具体的模拟中，本文所有的数据均是模拟1 000个粒子经历100 s的运动，这是因为改进欧拉法数值解方程选取了较短的步长(h=0.001)．为了便于模拟，对式(4)进行无量纲处理得到

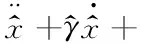
(10)

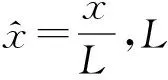
2 结果与讨论

2.1 活性布朗粒子在自由场中的运动

在图2中，我们模拟了活性布朗粒子和被动布朗粒子位移的分布，结果表明活性布朗粒子的位移呈现双峰分布．在正负半轴的双峰都是正态分布，峰的中心位置关于原点对称，出现粒子数的几率也近似相等，说明在自由场中，活性布朗粒子没有定向运动．为了与被动布朗运动比较，在图3中，我们模拟了被动布朗粒子位移的分布，发现被动布朗粒子在原点附近呈正态分布，也不存在定向运动.

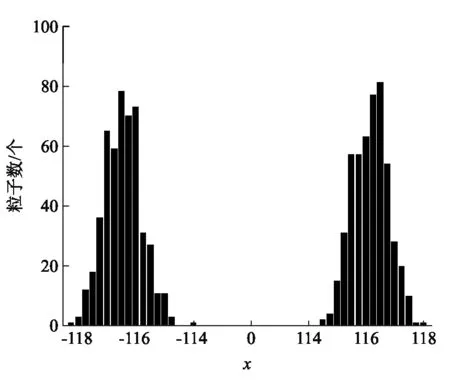
图2 活性布朗粒子位移分布[x=x0，y=y0代表位移在(x0，x0+0.25)范围内的粒子数为y0. t=100，γ=2.0，D0=0.01，d2=1.0，q0=3.0，c=0.1]

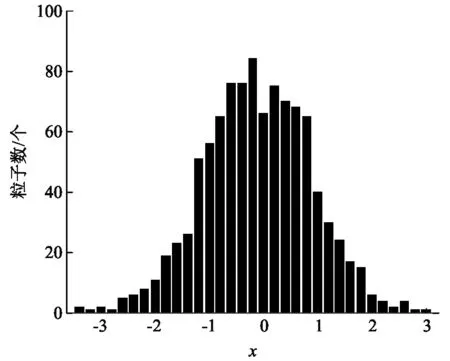
图3 被动布朗粒子位置分布(x=x0，y=y0代表着位移在[x0，x0+0.2)范围内的粒子数为y0. t=100，γ=2.0，D0=0.01)

无论是活性还是被动的布朗粒子，它们在自由场中都未发生定向运动，说明粒子的运动属于自由扩散．在图4中，我们分别计算了活性布朗粒子和被动布朗粒子的均方位移随时间的变化．从均方位移的数值上看，活性布朗粒子均方位移几乎是被动布朗粒子均方位移的104倍，表明活性布朗粒子扩散更主动，随机运动的距离更远．被动布朗粒子的均方位移与时间成正比，这符合爱因斯坦的理论[1]．而活性布朗粒子的均方位移随时间变化偏离了线性关系，类似于二次曲线，属于反常扩散行为[16].

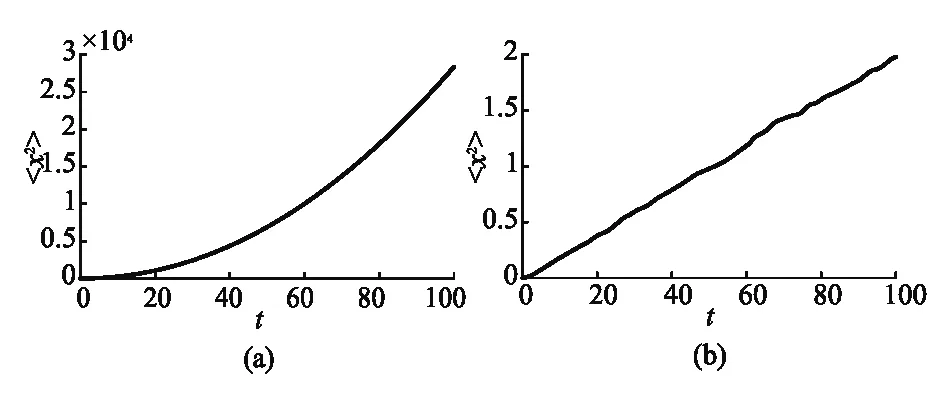
图4 活性和被动布朗粒子均方位移((a)活性布朗粒子的-t图像，(b)被动布朗粒子的-t图像. 其中：γ=1.0，D0=0.01，d2=1.0，q0=3.0，c=0.1)

2.1 活性布朗粒子在谐振子势中的运动

通常用谐振子势表示单分子实验中光阱对粒子的作用，本文选取二维谐振子势:

(11)

这个势能产生与位移相反的力：F=-k(x+y).

在谐振子势中，首先在一定的时间内分别模拟了活性布朗粒子和被动布朗粒子的运动，如图5 所示，我们观察到在谐振子势中粒子的自由扩散受到了限制，对比图5(a)和(b)还可以看出一定时间内活性布朗粒子扩散区域更大．然后，我们研究了劲度系数k对活性布朗粒子运动的影响， 如图6所示．我们可以看出：当k变小时，粒子的均方位移整体变大，图像上下震动的幅度变大，粒子达到平衡所需的时间变长；而k增大时，粒子的均方位移整体变小，图像上下震动的幅度变小，粒子达到平衡所需的时间变短．同时，我们发现在谐振子势中粒子的平均位移接近零，这说明在谐振子势中，粒子运动并没有产生定向运动.

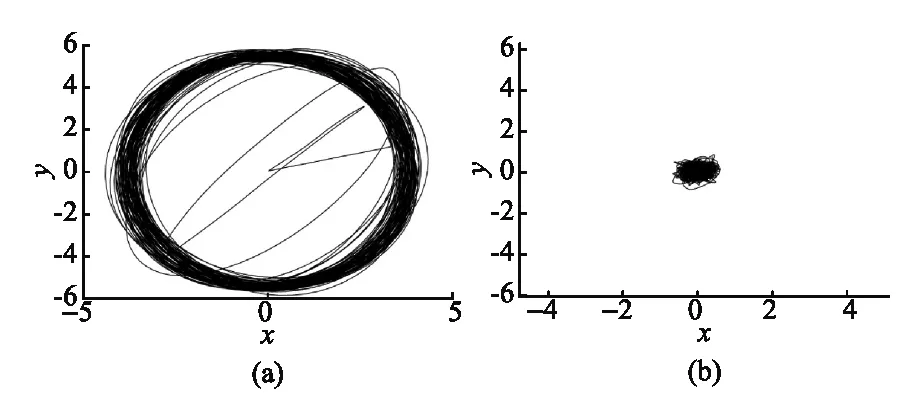
图5 粒子在二维谐振子势中的运动((a)活性布朗粒子；(b)被动布朗粒子. 其中：γ=0.2，D0=0.01，d2=1.0，q0=3.0，c=0.1，二者模拟时间均为100 s)

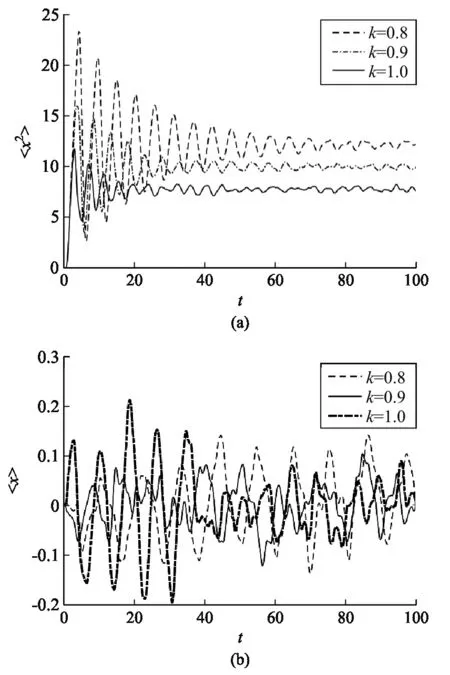
图6 谐振子势中活性布朗粒子均方位移和位移平均图像((a)均方位移；(b)位移平均. 参数设置： γ=1，D0=0.01，d2=2.0，q0=3.0，c=0.1)

2.3 活性布朗粒子在非对称周期势中的运动

以上研究表明，活性布朗粒子在自由场和对称的谐振子势中不存在定向运动，因此，我们考虑非对称周期势对粒子运动影响，选取组合正弦函数来模拟非对称周期势:

(12)

x0是调配周期函数,使x=0时，V为最小值，在式(12)中，经过计算选取x0=-3.239．V0用来调节势垒高度．在这个周期势中，势能变化较慢一侧为a侧，另一侧则为b侧．首先，在相同的势垒高度和模拟时间条件下，我们计算了活性布朗粒子在非对称周期势中的位移分布，同时比较了被动布朗的情况，如图7所示.

图7 非对称周期势中布朗粒子的运动((a)活性布朗粒子位移分布；(b)被动布朗粒子最终位移分布．活性布朗粒子参数设置：γ=1，D0=0.01，d2=2.0，q0=2.5，c=0.1，V0=1/2．被动布朗粒子参数：二者模拟时间均为100 s)

从图7我们可以观察到活性布朗粒子的位移分布不再对称，出现了明显的定向运动，而被动布朗粒子的位移分布相对初始位置是对称的，说明没有出现定向运动．然后，我们研究了势垒高度对活性布朗粒子平均速度的影响，如图8所示．根据F.Schweitzer等人[10]提出了活性布朗粒子维持“上坡”运动的限制条件:

(13)

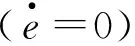
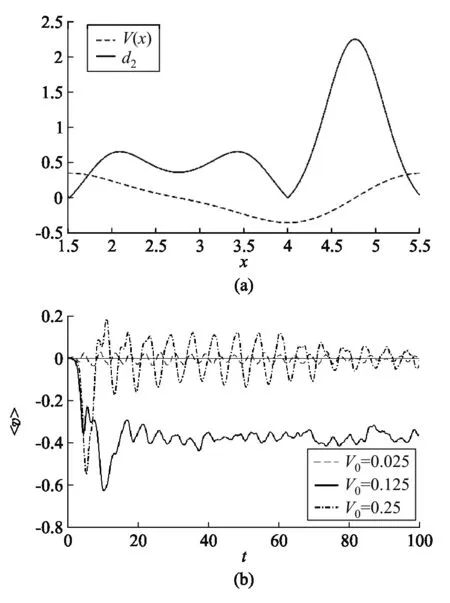
图8 (a) d2和V(x)的示意图,q0=1.0，γ=1.0，V0=1/8．(b) 不同V0下活性布朗粒子的平均速度-t时间图像，参数：γ=1.0，D0=0.01，d2=1.0，q0=1.0，c=0.1

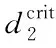
3 结论

细胞内活性物质的自推进运动一直是生物和医学研究的热点问题，而活性布朗粒子模型是研究自推进运动基础的模型之一．本文基于经典的活性布朗运动模型，首先对方程进行无量纲处理，然后采用预估-修正算法数值解方程，最后用Matlab作图分析运动情况.

在自由场中，我们的计算表明活性布朗粒子不存在定向运动，而且均方位移随时间非线性变化．其次，在谐振子势中，我们发现粒子的自由扩散受到了限制，但在相同时间内，活性布朗粒子的扩散区域比被动布朗粒子大．最后，在非对称周期势中，我们计算了活性布朗粒子的位置分布，同时计算不同势垒高度下，活性布朗粒子平均速度随时间的变化，结果表明活性布朗粒子能否将储存子库的能量转化为定向运动依赖于势垒高度．本研究有助于理解为生物中主动输运的物理机制，同时可以加深我们对非平衡统计物理的认识.