Spark平台下基于优化BP神经网络模型的接触疲劳剩余寿命预测

刘致远，刘渊博，杨 峰，鲁凯旋，刘 妤

(重庆理工大学 机械工程学院， 重庆 400054)

随着物联网、智能传感器、无线通信等技术的飞速发展及其在机械领域的广泛应用，如何在大数据背景下实现对历史数据和实时数据的深入挖掘和利用，以准确把握机械装备/零部件的健康状况，精准分析其性能退化趋势，已经成为状态监测领域的研究热点之一[1-2]。

国内外很多学者开展了剩余寿命预测模型的研究，其中，数据驱动的神经网络具有强劲的非线性映射能力，能够较好地解决多参数拟合问题，成为回归预测的常用模型之一[3]。Gebraeel等[4]将BP神经网络模型用于轴承剩余寿命预测，利用轴承全寿命周期内的振动数据，实现了一种加权性能退化系数的轴承剩余寿命预测方法。高宏力等[5]以实验采集的多传感数据作为网络训练的输入向量，建立了基于 BP 神经网络的滚珠丝杠副寿命预测模型，实现了对滚珠丝杠副系统的剩余寿命预测。Tian等[6]建立了神经网络寿命预测模型，通过对历史数据和实时数据进行威布尔失效函数的拟合匹配，并以其作为神经网络模型的输入，实现了对泵轴承的剩余寿命预测。Zhang等[7]采用遗传算法对BP神经网络的权重系数进行了全局优化，提高了刀具剩余寿命预测精度。Wang等[8]结合时间序列分析法和BP神经网络，实现了冷却风机的剩余寿命预测，且预测寿命数据与实际寿命数据具有较好的一致性。刘咏鑫等[9]采用混沌序列优化BP神经网络，构建了多参数关联的预测模型，实现了对变压器剩余寿命的高精度预测。

接触疲劳是基础部件失效的主要原因之一[10]，实现对接触疲劳试样的精准状态监测和准确寿命预测具有重要意义。现有文献报道中所涉及的串行算法在单机运行环境下迭代运算时间很长，难以处理和分析海量的监测数据。为此，本文结合自主研发的滚动接触疲劳试验装备的运行监测数据，提出了一种Spark平台下基于优化BP神经网络模型的接触疲劳剩余寿命预测方法，为实现大数据背景下接触疲劳剩余寿命的准确预测奠定基础。

1 监测数据处理与剩余寿命计算

1.1 滚动接触疲劳试验装备简介

针对现有疲劳试验装备存在的疲劳失效判定需停机目测、接触疲劳数据难以精准获取、试验劳动强度大等问题，项目组自主研发了新型滚动接触疲劳试验装备，如图1所示。该装备实现了对振动、温度、扭矩和载荷等多种信号的实时监测。

图1 自主研发的滚动接触疲劳试验装备

1.2 特征选取与数据预处理

不同的特征对退化的敏感性和相关性是不同的。准确实现接触疲劳剩余寿命预测的前提是特征时序能够真实反映试样的退化过程，因此，需要结合一些评价指标对退化特征进行选取。综合考虑相关性、单调性和鲁棒性3个评价指标，建立如式(1)所示的线性组合方程，通过多目标优化函数选取权值较大的特征作为退化敏感特征。

(1)

式中：W为多目标优化函数；Y为备选的特征序列集合；ωi(i=1，2，3)为3个评价指标的权重。相关性、单调性和鲁棒性3个评价指标的定义式分别如式(2)(3)(4)。

(2)

(3)

(4)

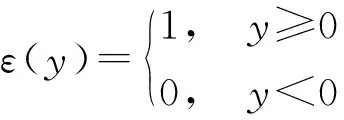
通过对退化敏感特征的分析和提取，最终选择振动信号的有效值、峰峰值、最大值、峭度因子、裕度因子、脉冲因子、偏度7个时域指标，平均频率、频率方差2个频域指标，以及温度参数作为输入特征变量。此外，考虑到滚动接触疲劳试验过程中，传感器采集装置受外界坏境影响可能导致传感器采集信号出现突变的异常值，因此，对采集信号进行基于拉依达法则[11]的异常值判断及处理，当某时刻采集数据被认定为异常时，用前一时刻值替换。同时，为了消除不同特征指标量纲差异对数据分析效率与精度的影响，采用最大最小归一化[12]方法对数据进行预处理。

1.3 剩余寿命计算

滚动接触疲劳试样退化状态的评估值反映了试样当前的健康状态，结合试验的历史运行数据可以预测试样的剩余寿命。滚动接触疲劳实验过程中，试样一般会经历3个阶段，即正常期0～t1、衰退期t1～t2、快速失效期t2～t3，如图2所示。

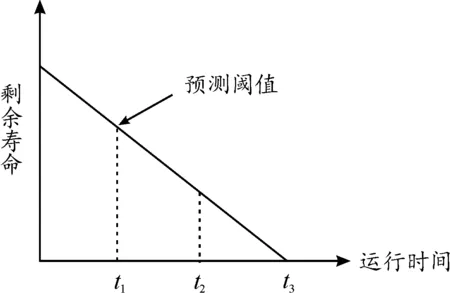
图2 滚动接触疲劳试样剩余寿命

正常期内，试样表面无缺陷发生，排除其他干扰因素，特征信号持续平稳且没有明显变化趋势，无法实现对试样的剩余寿命预测。进入衰退期后，记tr为试样自t1开始计算的已运行时间，f(tr)为tr时刻的退化状态评估值，则滚动接触疲劳试样在tr时刻的剩余寿命lr定义为[13]：

(5)

式中：退化状态评估值的范围为(0，1]，其值趋近于0表示试样完好无损，为1表示试样已经疲劳失效。

2 基于Spark平台的滚动接触疲劳剩余寿命预测模型

2.1 BP神经网络优化模型

BP神经网络是利用输入信号前向传播、误差反馈信号反向传播和梯度下降的原理，通过链式求导法则更新权值，从而达到减小误差、获得理想输出的目的。

设定BP神经网络为3层结构，即1个输入层、1个隐藏层和1个输出层，如图3所示。

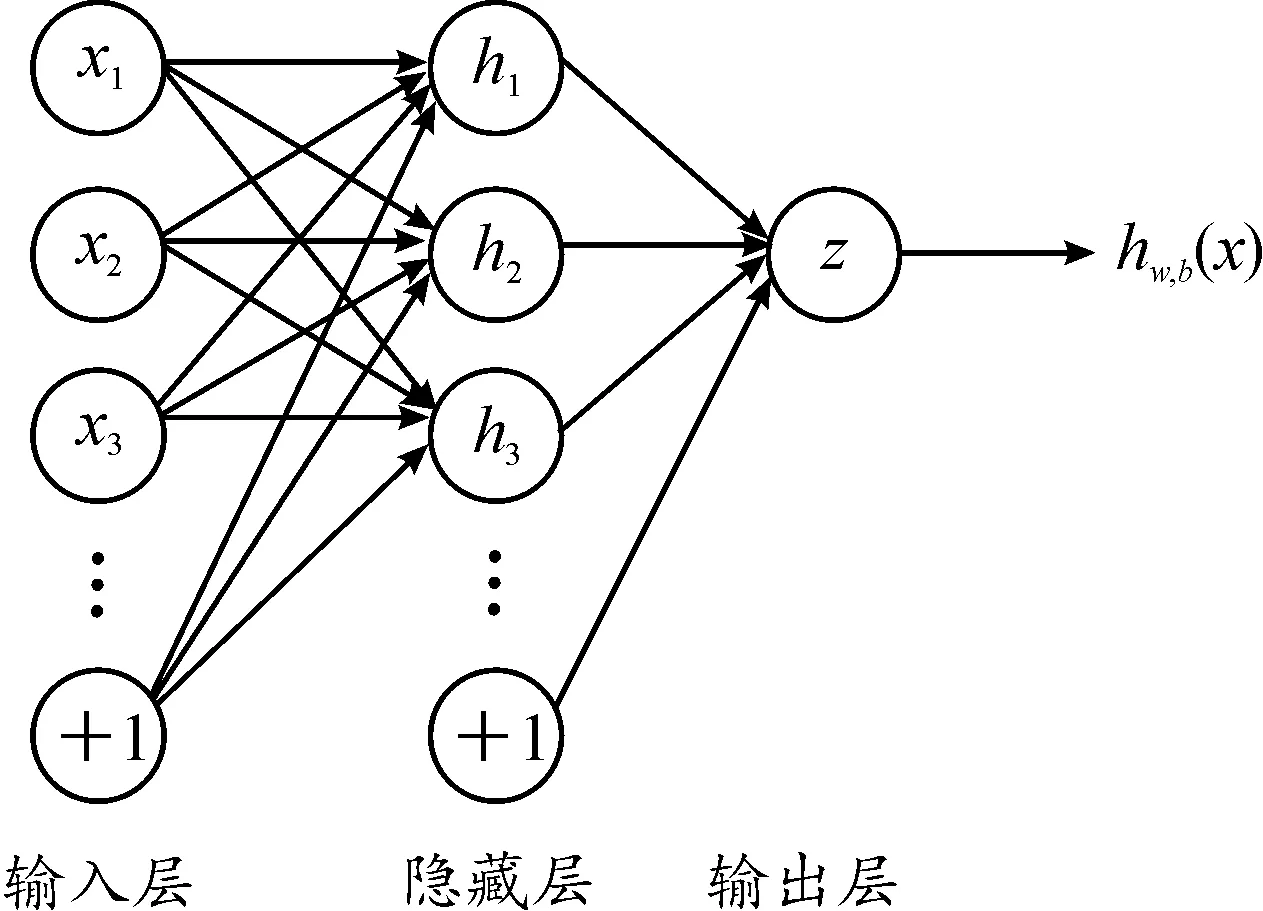
图3 神经网络预测模型

记k表示神经网络的层数，fk(·)表示第k层神经元的激活函数，W(k)表示第k层与k+1层神经元间的权重矩阵，b(k)表示第k层与k+1层神经元的偏置项，z(k)表示第k层神经元的状态，a(k)表示第k层神经元的输出值。

1) 对神经网络进行前馈计算，通过逐层的信息传递计算，得到最后输出hw，b(x)。

z(k)=W(k)·a(k-1)+b(k)

(6)

a(k)=fk(z(k))

(7)

一个m组训练样本的数据集(x(i)，y(i))(1≤i≤m)，整体误差函数为：

(8)

式中：第一项为均方差，第二项为L2正则化，其目的是减小权重的幅度，防止过拟合，提高预测模型的泛化能力。

为了提高学习模型的健壮性和泛化性，防止模型过拟合，本文采用hintion提出的Dropout方法[14]减少神经元之间复杂的共适应关系。

2) 对神经网络进行误差反向传播，采用小批量梯度下降算法，对于Batch_size为n，按照式(9)(10)对参数W和b进行多次迭代更新，最后输出模型参数。

(9)

(10)

传统的BP神经网络模型，学习率为固定值，由此可能导致：当学习率偏大时，引起学习震荡甚至发散，从而无法收敛；当学习率偏小时，收敛过于缓慢，网络拟合效果差，且训练过程中易陷入局部最小值。为此，本文对周期性学习率进行优化，提出一种指数衰减周期性学习率，定义：

(11)

式中：Icur为当前迭代次数；λ为指数衰减系数；I为总迭代次数；αmin、αmax分别为学习速率最小值和最大值；Trange为一个学习周期中迭代次数；Tcur为继上次周期后的迭代次数。

结合式(11)得到学习速率随迭代次数的变化曲线如图4所示。在训练过程中，每一周期结束后学习速率有很大的提升，这有助于退出一个局部低点并继续搜索最佳参数；在找寻全局最优解过程中，学习速率将以指数方式衰减，这有利于网络收敛，提高精度。

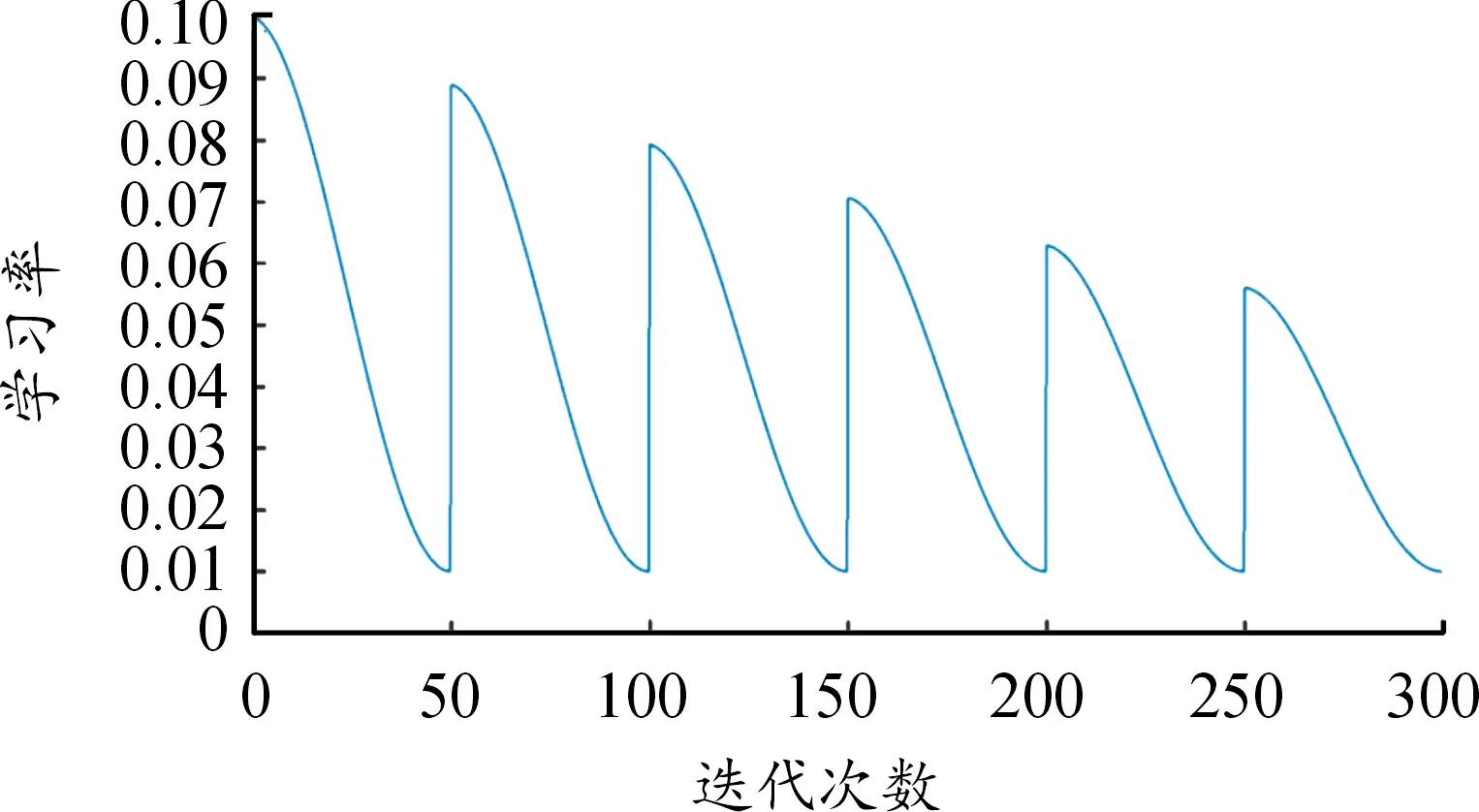
图4 学习率变化曲线

式(11)中，指数衰减系数λ表征每个周期间学习率的差异。由经验法则可知[15]，最佳学习速率通常低于最大收敛学习率的1/2，应将基本学习率设置为最大收敛学习率的1/3或1/4，为使学习率变化在一个合理的范围内，考虑λ的值为2～4；Tcur表示一个学习周期，为达到训练结果精度的峰值，训练结束时学习速率应处于最小值，则模型训练迭代次数应为学习周期的整数倍，即I应为Trange的整数倍；为确定学习速率边界值，当建立新的神经网络模型架构时，应从训练集分割少量数据在神经网络中运行几个周期，同时令学习速率在低和高学习率值之间线性增加并观测其变化对预测精度的影响，当预测精度开始明显增加，设定此时学习速率值为αmin，当预测精度上升开始减慢，即出现波动或开始下降，设定此时学习速率为αmax。

2.2 基于Spark平台的模型及算法实现

Spark是一个基于内存计算的开源集群计算框架[16]。相比于Hadoop，Spark可以将计算过程中的输出和结果保存在内存中，并联执行多个Stage时，通过内存进行数据运算，从而不再需要读写HDFS，运行速度可提升100倍。因此，Spark更适用于数据挖掘与机器学习等需要迭代的MapReduce算法。

针对滚动接触疲劳试样剩余寿命预测，提出的分布式神经网络模型实现流程如图5所示。首先，对采集到的样本数据存储在HDFS分布式文件系统中，进行预处理与特征提取并将其封装在类data[]中。类data[]由向量x与向量y组成，其中x代表模型输入向量，y代表退化状态评估值。其次，在Spark计算框架下从整个训练数据集D随机分段抽取10%数据组成数据集D1，在Master节点设置神经网络模型初始参数，并在单机环境下作周期性学习率参数设置测试。最后，经测试得到最佳学习率设置参数进行模型训练，具体如下：① 将整个训练数据集D分成m组样本数据集分发至集群中m个节点，通过Spark中的算子parallelize()将其转化为RDD集；② 将Master节点中的全局神经网络模型初始参数广播至各个Worker节点。各Worker节点接收到Master节点传来的权重参数后对各自神经网络结构进行初始化，并行处理数据进行迭代运算；③ 将计算结果返回于return[]集合中，再次RDD转化后，输出至Master节点，利用算子map()、reduce()计算出最终解weights[]集合；④ 利用weights[]集合构建滚动疲劳接触试样剩余寿命预测模型，使用测试集进行测试模型评估。

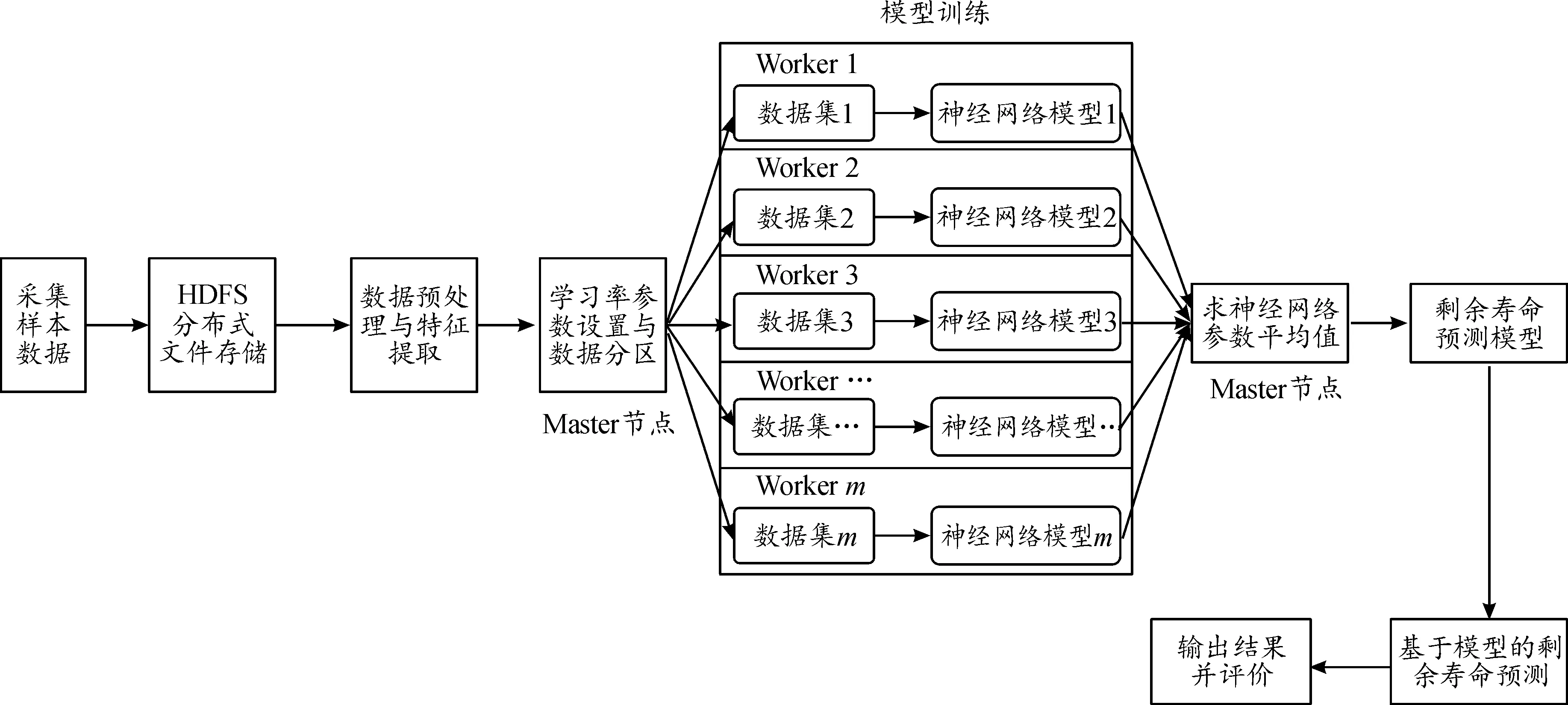
图5 分布式神经网络模型实现流程框图

基于Spark的寿命预测实现流程如图6所示。

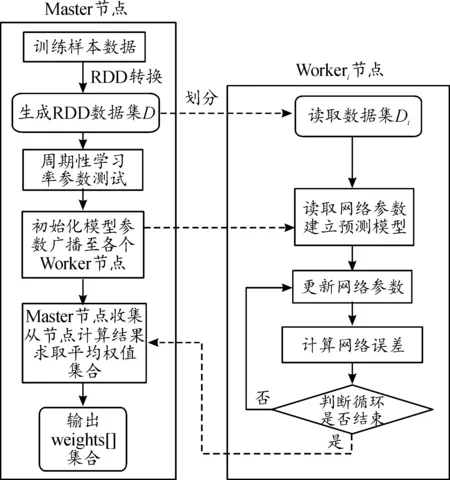
图6 基于Spark的滚动接触疲劳寿命预测算法流程框图

3 实验设计与结果分析

3.1 实验设计

搭建了基于Hadoop的分布式文件系统，采用Spark并行计算框架，以Mysql作底层存储。集群由1个Master节点、3个Worker节点构成，CPU为Inter Xeon E5-2650 @2.40 GHz，操作系统为Centos 7.4，Hadoop版本为2.7，Spark版本为2.2，JAVA版本为JDK1.8，编译语言为Scala2.11.7，编译工具为IntelliJ IDEA 2019.6。

为了验证剩余寿命预测模型的有效性，开展了滚动接触疲劳实验。实验用滚子试样材料为40Cr(采用正火工艺处理)，转速为2 000 r/min，加载载荷为2 680 N，数据采样频率为10 kHz，传感器每隔20 s采集一次数据，每次采样时长为0.1 s。选用5组滚子进行滚动接触疲劳实验，从5组数据集中随机选择4组数据集构成训练数据集，剩下1组作为测试数据集。

设计神经网络模型的输入层神经元个数为10，隐藏神经元个数为12，输出层神经元个数为1，输出变量为退化状态评估值，隐含层的激活函数和输出层传输函数采用sigmoid对数函数，Dropout系数设为0.083 3，正则化系数为0.01，Batch_size为256，迭代次数为500，期望误差为0.000 1，指数衰减系数为3，周期大小为50，最大学习率为0.1，最小学习率为0.01。

3.2 实验结果及对比分析

对测试数据集进行预处理后得到4 554组有效数据。根据式(5)与模型输出的退化状态评估值计算得到寿命预测值。模型输入特征变量和预测结果如表1所示。

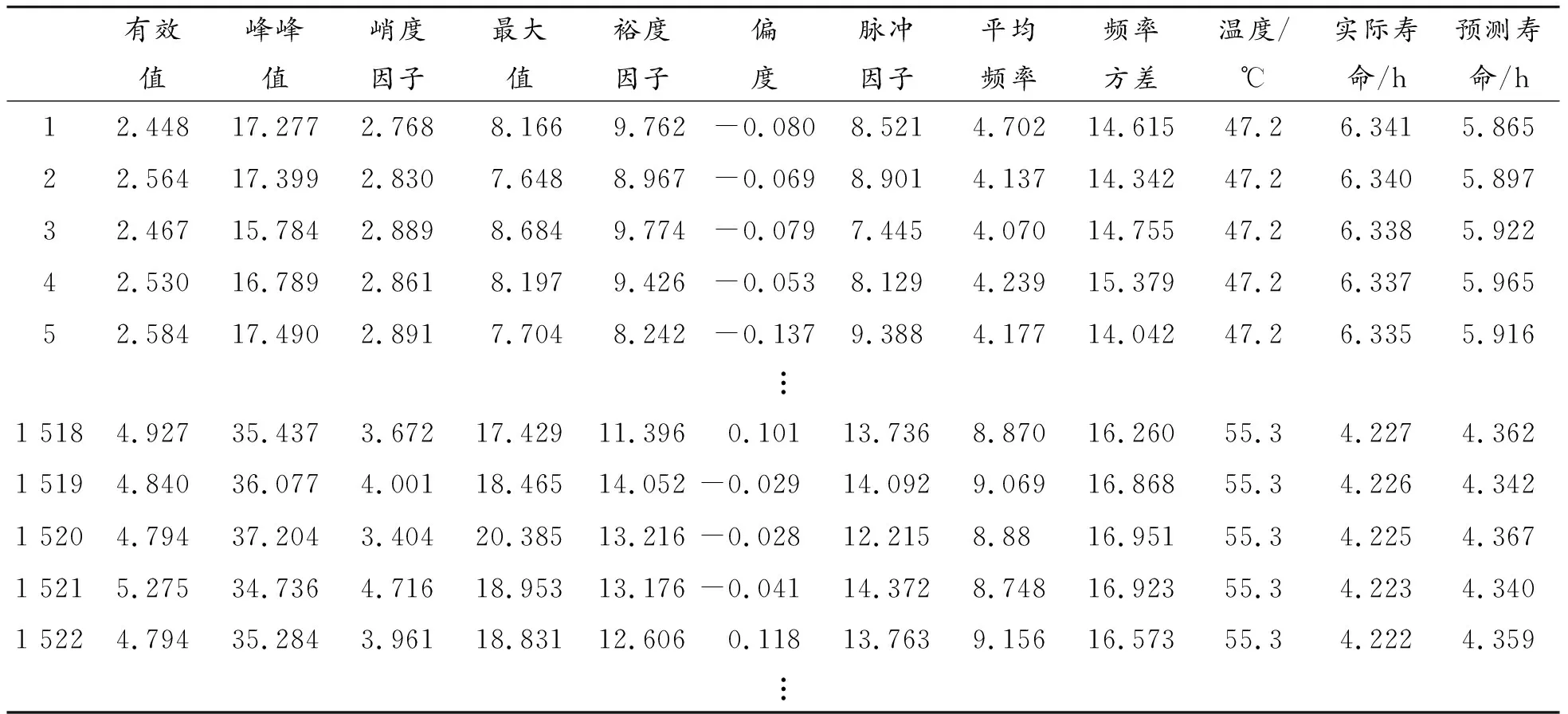
表1 疲劳试验数据和预测结果

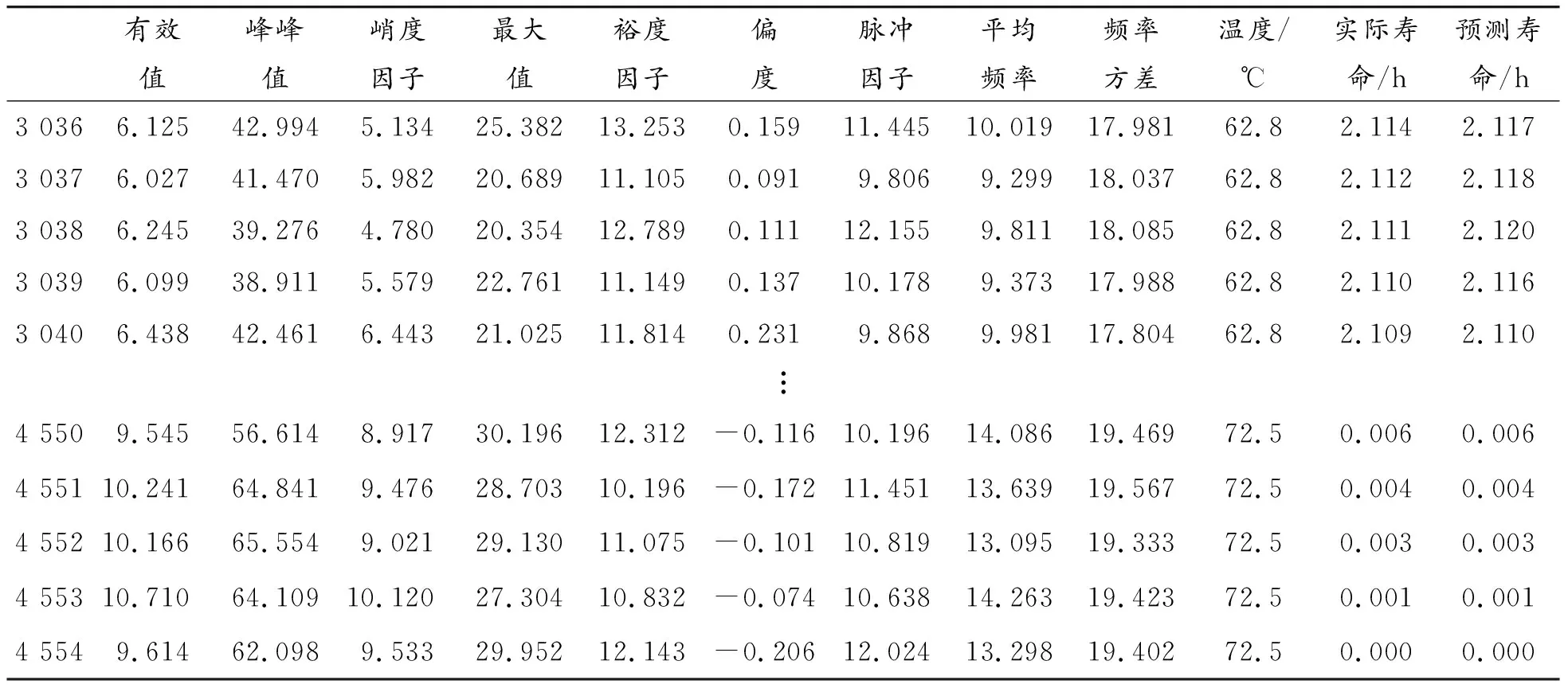
续表(表1)

在相当实验条件下，对比分析了基于不同算法、不同预测模型、不同计算平台的滚动接触疲劳剩余寿命预测结果，所涉及的评价指标主要包括最大最小相对误差RE、均方根误差RMSE、平均绝对百分比误差MAPE，各评价指标的计算式[17]分别为：

(12)

(13)

(14)

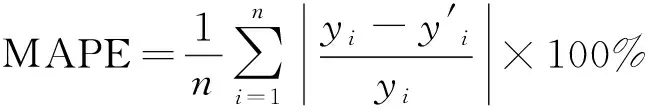
(15)

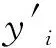
1) 基于不同学习率算法的对比分析

在同样的实验条件下，对比分析了本文学习率算法与常用Adagrad自适应学习率算法、传统固定学习率算法在运算过程中的平均绝对百分比误差MAPE收敛走势，如图7所示。可以看出：① 在经历180次迭代后，本文学习率算法的平均绝对百分比误差小于其他2种算法，这表明本文算法的收敛精度和全局寻优能力高于其他2种算法；② 170次迭代后的精度大于自适应学习率算法200次迭代后的精度，模型具有更快的收敛速度。

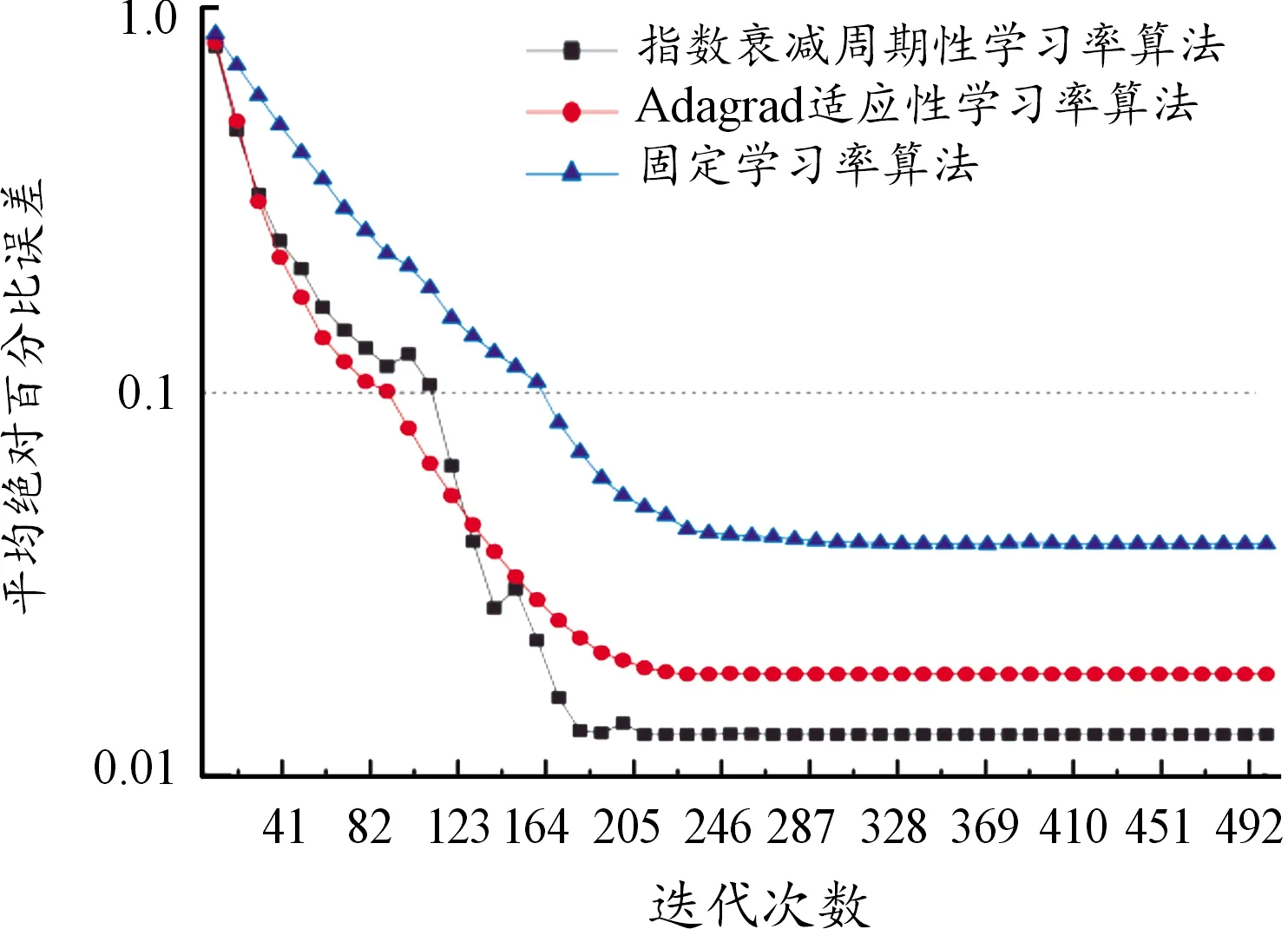
图7 不同算法下的平均绝对百分比误差

2) 基于不同预测模型的对比分析

在同样的实验条件下，对比分析了基于Spark平台的优化BP神经网络模型与传统神经网络模型、支持向量回归机SVR模型的预测性能，如图8所示。

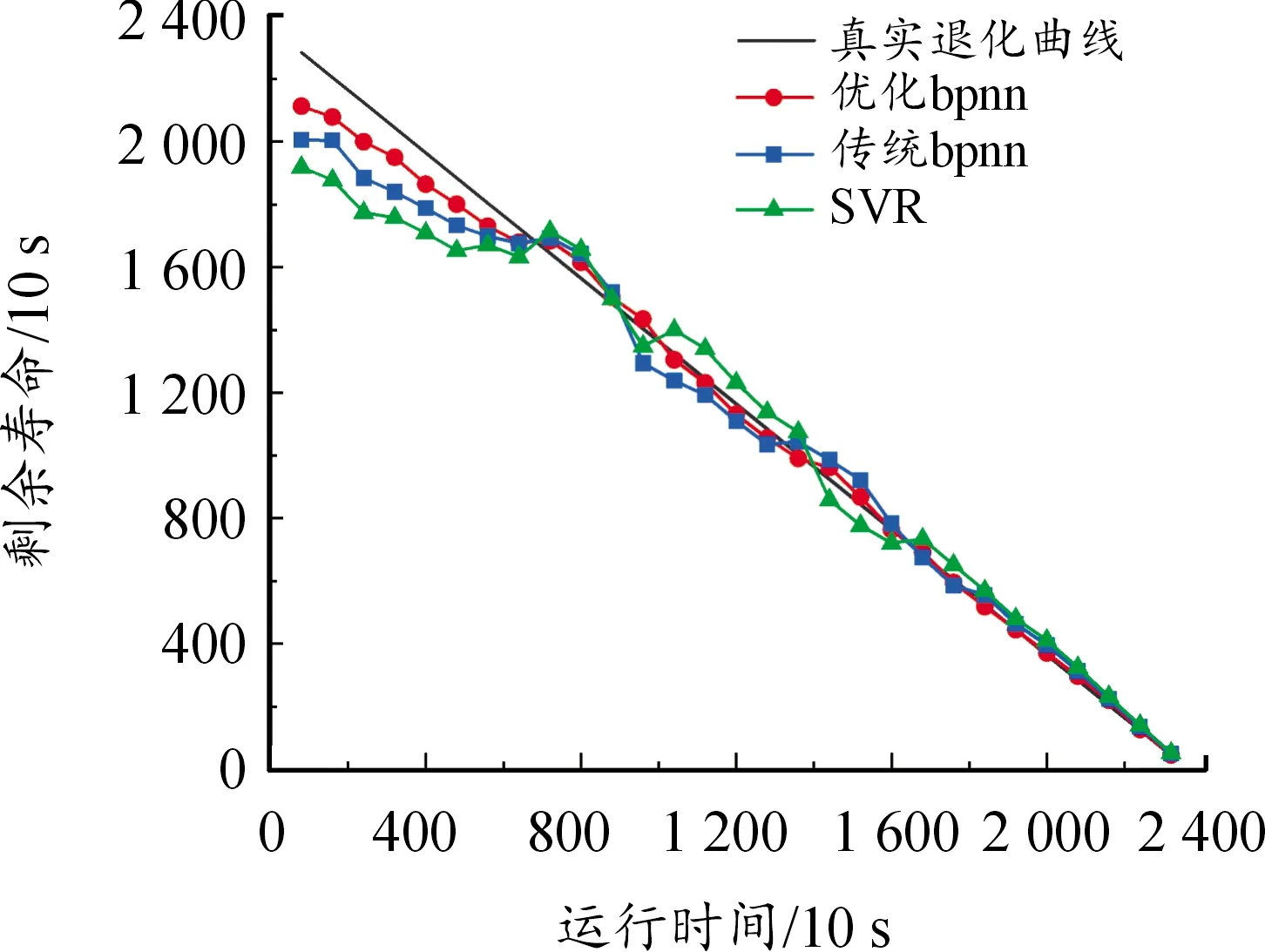
图8 基于不同模型的剩余寿命预测

从图8可以看出：① 虽然在滚子试样疲劳退化初期，本文基于优化BPNN模型的剩余寿命预测值与实际值相差较大，但误差仍小于其他2种模型；② 随着运行时间的增加，优化BPNN模型的剩余寿命预测值逐渐逼近真实值，且预测曲线与其他2种模型的预测曲线相比更为平滑，误差变化较小，与真实剩余寿命曲线更接近。

进一步分析3种模型的剩余寿命预测误差，如图9、表2所示。可以看出：① 基于优化BPNN模型的最大、最小相对误差RE分别为7.432%和0.017%，而基于传统BPNN模型和SVR模型的最大、最小相对误差分别为12.198%和0.234%、16.533%和1.144%，表明模型具有更好的泛化性能；② 基于优化BPNN模型的均方根误差为0.624，而基于传统BPNN模型和SVR模型的均方根误差分别为0.746和1.332，表明预测滚动接触疲劳剩余寿命优化BPNN模型具有更高的稳定性；③ 基于优化BPNN模型的平均绝对百分比误差为2.685%，而基于传统BPNN模型和SVR模型的百分比误差分别为7.357%和11.86%，表明优化BPNN模型的预测精度更高，预测更加准确。

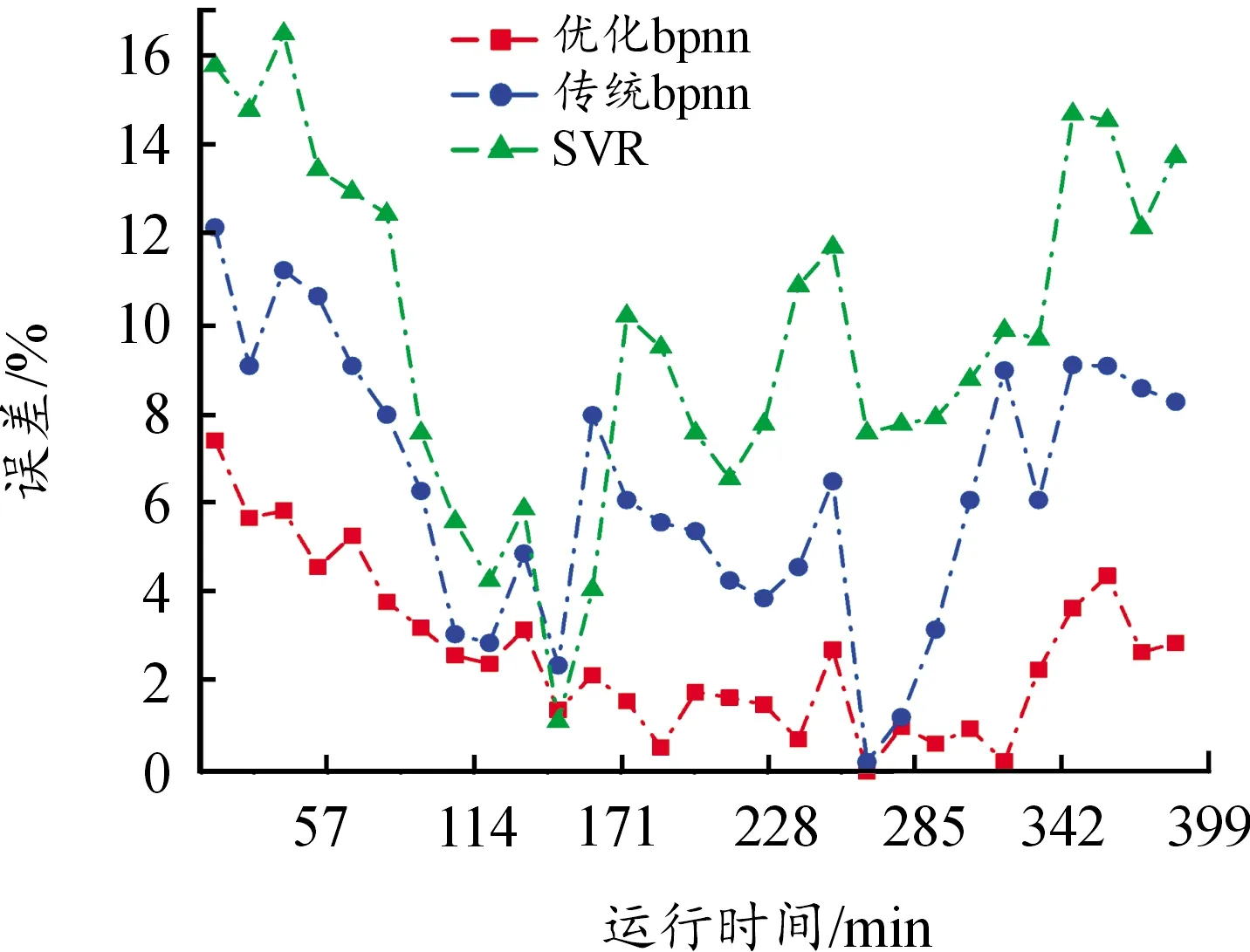
图9 基于不同模型的预测结果误差

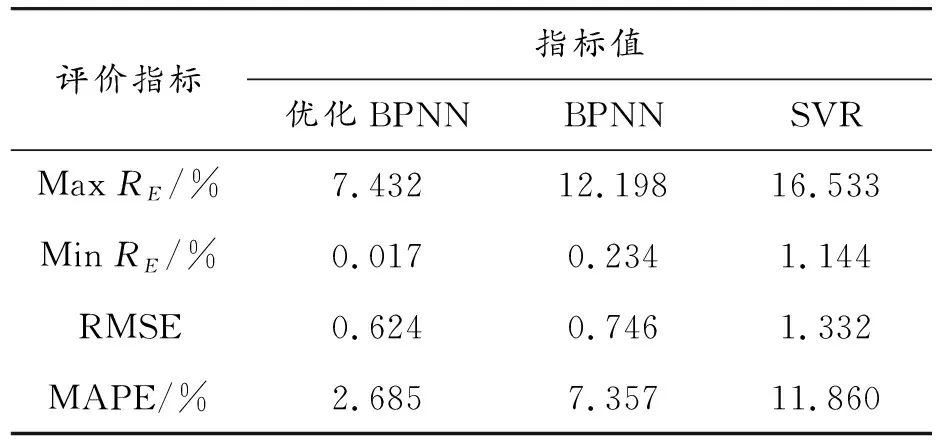
表2 基于不同模型的评价指标对比

3) 基于不同计算平台的对比分析

对比分析了基于Spark平台和Hadoop平台预测剩余寿命时的并行计算效率，如图10所示。可以看出：① 当处理数据量小于1 G时，2种框架下的计算效率差别并不大；② 当样本数据量超过4 G 时，Spark平台所需要的时间小于Hadoop平台，且这种差距随着样本数据量的增大而愈加明显，表明基于内存的迭代式计算Spark平台在大数据背景下的剩余寿命预测更具优势。

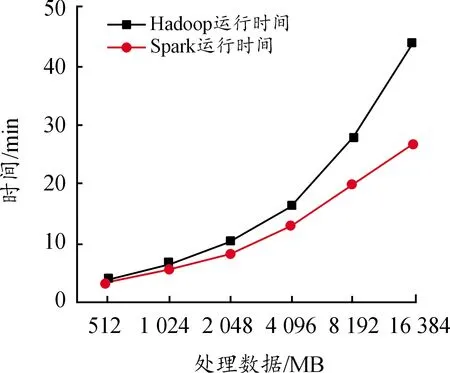
图10 基于不同平台的计算效率

4 结论

结合自主研发的滚动接触疲劳试验装备的运行监测数据，提出了一种Spark平台下基于优化BP神经网络模型的剩余寿命预测方法，实现了接触疲劳剩余寿命的准确预测。实验结果表明：基于指数衰减周期性学习率算法相较原始固定学习率算法和Adagrad学习率算法具有更好的收敛性能；所建立的优化BP神经网络模型相较传统BPNN模型和SVR模型具有更高的预测精度；Spark平台相较Hadoop平台具有更高的数据处理效率，更适用于海量、多维数据的计算。