车路协同环境下的双雷达车辆检测和跟踪优化方法

李 旭，秦嗣牧，王建春

(山东科技大学 交通学院， 山东 青岛 266590)

车路协同基于传感探测、无线通讯等技术感知车路信息，并通过车路、车车通信设备进行信息共享和交互，实现车辆和基础设施之间智能协同与配合，达到优化利用系统资源、改善道路交通安全、缓解交通拥挤的目标。多传感器数据融合是车路协同的关键技术之一。众多学者针对多传感器环境感知领域进行了相关研究。向易等[1]通过车载双雷达的形式估计前方目标位置状态；王战古等[2]提出了一种基于车载毫米波雷达和摄像头信息融合的检测方法，通过毫米波雷达获取图像中的感兴趣区域，再利用图像处理的方法识别车辆；同样地，刘志强等[3]提出了基于GNN-DS来进行毫米波雷达和摄像头的信息融合算法，以保证检测精度；薛培林等[4]考虑激光雷达与相机融合的车辆识别方法，利用改进yolov3-tiny算法提高目标检测准确率。在考虑路侧和车载传感器融合方面，李泽等[5]和谢伯元等[6]都利用卡尔曼滤波算法进行数据融合，但未考虑目标在非线性运动状态下的预测精确度。

针对上述研究，提出了一种基于无迹卡尔曼滤波(unscented Kalman filter，UKF)算法，利用统一坐标系的路侧毫米波雷达和车载毫米波雷达数据进行车辆行驶轨迹和速度的预测和更新。该算法考虑车辆非线性行驶工况，在无人驾驶多传感器数据融合领域具有应用前景。

1 雷达数据预处理

选用2个同规格AER毫米波雷达，其更新频率为50 ms，以雷达自身为坐标系原点，可以检测目标相对雷达的距离、速度等信息，检测距离为远距170 m，近距70 m，距离精度为±0.20 m(远距)，±0.10 m(近距)，速度精度为±0.1 km/h。车载雷达和路侧雷达安装位置及检测区域如图1所示，由图可知，如果与前车距离过近，车载雷达会受到前车遮挡而看不到对向车辆，因此需要与路侧毫米波雷达数据融合才可得到完整的车路数据。雷达数据融合估计算法流程见图2。

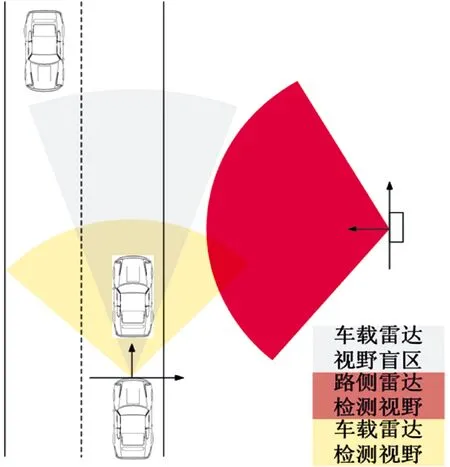
图1 2种雷达安装位置及检测区域示意图

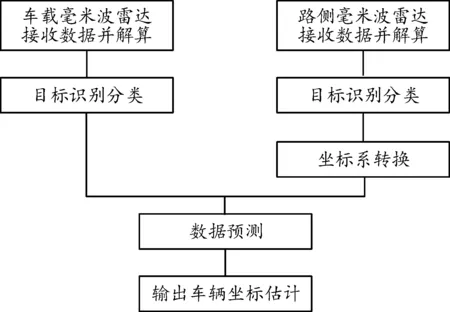
图2 雷达数据融合估计算法流程框图

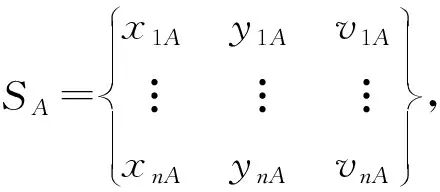
1.1 目标识别分类

采用基于密度的自适应DBSCAN聚类算法，该算法可以识别任意形状簇，且利用数学统计分析的方法定义聚类所需的参数Eps与MinPts，避免识别过程中的人工干预。此处采用横/纵向距离、速度3种属性来进行聚类，以提高车辆与车辆、车辆与静态物体的聚类准确性，并将聚类出的簇作为车辆的坐标点。

通过给定数据集D={d(i)，i=0，1，2，3，…，n}，计算数据集D的距离分布矩阵[7]：

Dn×n={Dist(i，j)|1≤i≤n，1≤j≤n}

(1)

式中：Dn×n为n×n的实对称矩阵；n为数据集D所包含的对象数量；Dist(i，j)为数据集D中第i个对象到第j个对象的距离。将矩阵D每行以升序排列，则第1列元素所组成的距离向量D0表示对象到自身的距离，全为0。第K列元素构成所有数据点的K-最近邻距离[8-9]向量DK，对Dk列进行求平均值，作为Eps参数列表，采用数学期望法生成MinPts参数列表。对于给定的Eps参数列表，依次求出每个Eps参数对应的Eps邻域对象数量，并计算所有对象的Eps邻域对象数量的数学期望值，作为数据集D的邻域密度阈值MinPts参数[10]，表示为：

(2)

式中：Pi为第i个对象的Eps邻域对象数量；n为数据集D中的对象总数。如果MinPts不变，Eps取值过大，会导致1个簇内包含范围过大；Eps过小，会导致簇分裂为多个小簇；如果Eps不变，MinPts的值取得过大，会导致聚类成簇的条件过于严苛；MinPts过小，会导致核心点分裂。随着Eps增加，MinPts参数值呈现平稳状态，因此选择进入平稳状态的初始Eps值和MinPts值，聚类效果最优。

S集合是已知有7个簇类、共包含800个对象的数据集，分布如图3所示，以该数据集来验证自适应算法的合理性。

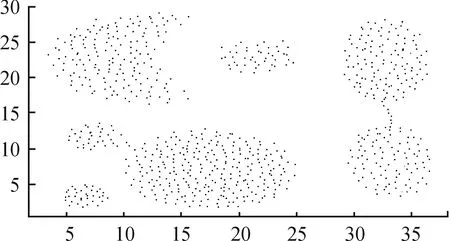
图3 S数据散点图

采用K-平均近邻法和数学期望法生成Eps候选值和对应的MinPts候选值如图4所示。

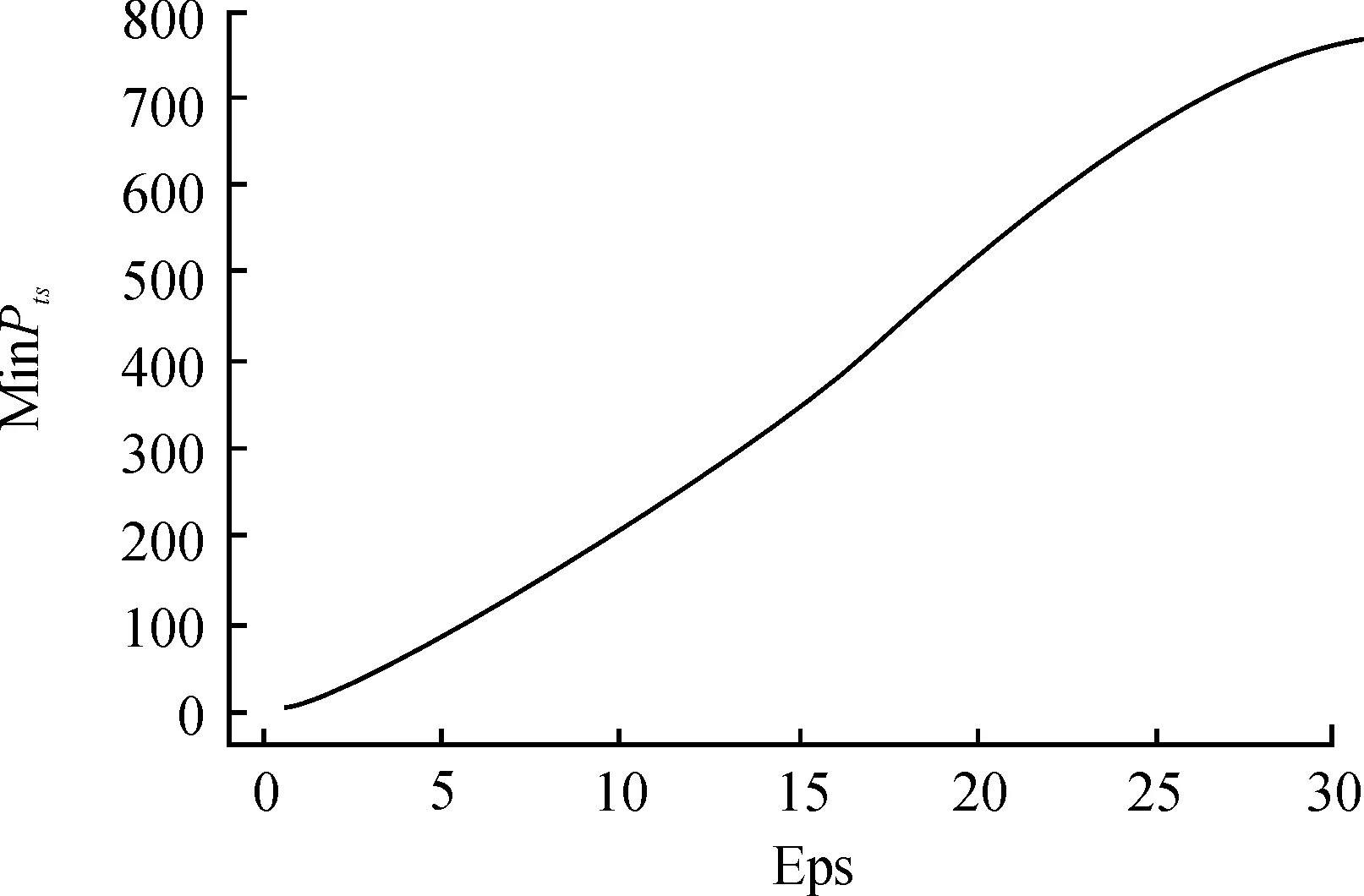
图4 Eps和MinPts候选值

图5展示了K-最近邻距离与簇数的对应关系，可以看出：当K=12时，簇数开始进入稳定阶段，到K=18时结束；此时根据计算对应的Eps=1.6，MinPts=32，聚类结果如图6所示。该数据集利用该组参数可以准确聚类出7个簇，以此证明本文自适应算法的有效性。

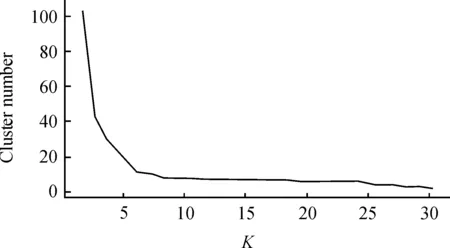
图5 K-最近邻距离对应的簇类数量折线图

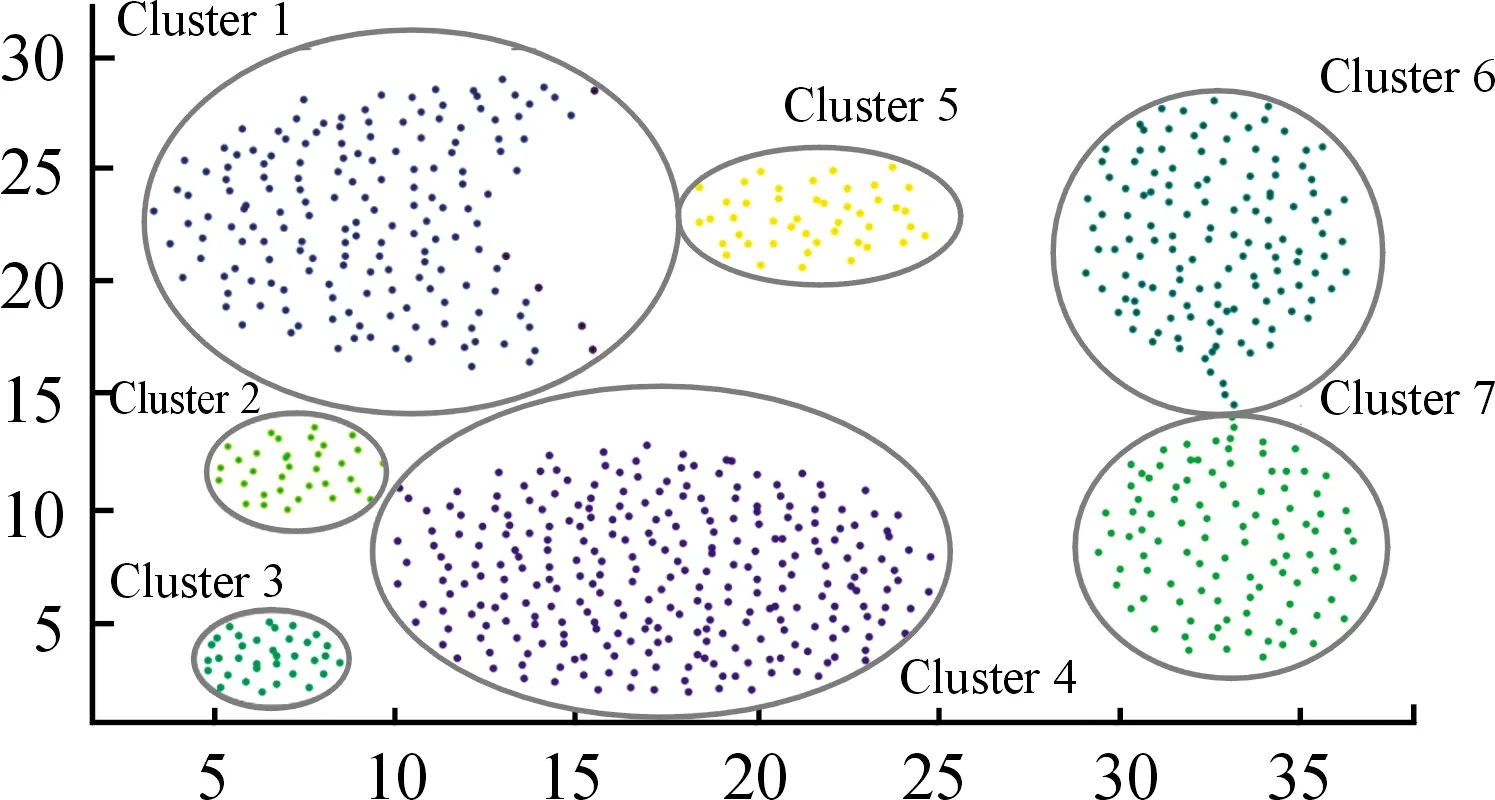
图6 S数据集聚类结果示意图

1.2 坐标系转换

为了更好地对同一物体在不同检测设备下的数值做出比较，采用特征点匹配的方式，先利用毫米波雷达检测易识别、特征值明显的静态障碍物，如道路中间的护栏，并通过最小二乘法拟合护栏的数据点，最后将路侧雷达点云根据拟合结果进行位置姿态矫正，具体步骤如下：

首先，利用密度聚类的方法分别建立2种雷达中护栏的数据集合，记为PA={p1，p2，…，pn}和PB={p1，p2，…，pn}；根据护栏的形状特征，采用直线模型进行拟合，对于集合P，随机抽样选取5个初始点拟合直线，计算所有点到该直线的距离，在预设阈值范围内点的数量记为最优点数[11]；再重新随机选取初始点进行拟合并计算，重复上述步骤500次；最后，比较单次最优点数最多的直线为拟合结果。由于时空连续特性，连续帧中护栏的位置偏差不会太大，因此，为了提高检测结果的连续性，将相邻帧的拟合结果进行叠加。

图7为护栏与其他车辆(2号车为自车)分别在自车雷达和路侧雷达检测下的相对位置和方向，o点为2个坐标系的原点，θ为2个护栏数据拟合出的直线夹角，前车对于自车的相对距离分别为：

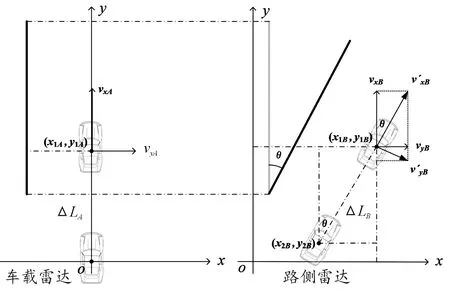
图7 路侧雷达数据转换示意图

(3)

(4)

式中： ΔLA和ΔLB分别为2个雷达下的相对距离；v′为根据θ合成的前车车辆行驶方向和侧向速度。

2 目标数据估计算法

路侧雷达数据经过相对距离转换后，与车载雷达处于同一坐标系中。采用无迹卡尔曼滤波算法，通过无迹变换使非线性系统方程适用于线性假设下的标准卡尔曼滤波体系[12]，具体流程如下：

一个n维非线性离散动态系统可以表示为[13]：

xk=f(xk-1)+wk

(5)

zk=h(xk)+vk

(6)

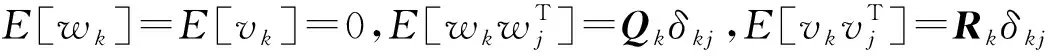
无迹卡尔曼滤波标准程序如下：

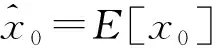
对于k≥1：

1) Sigma点取样。生成1组具有相关权值的确定性样本点[15]：

(7)

(8)

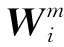
2) 时间更新。通过非线性函数变换样本点，计算预测的均值和协方差。

xi，k∣k-1=f(xi，k-1)，i=0，1，…，2n

(9)

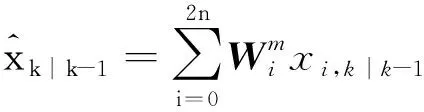
(10)

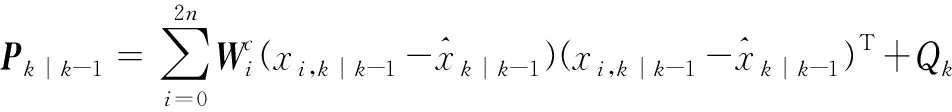
(11)

zi，k∣k-1=h(xi，k∣k-1)，i=0，1，…，2n

(12)

(13)

(14)

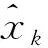
(15)

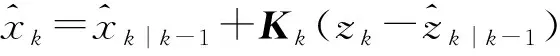
(16)

(17)

其中Kk为增益矩阵。

3 实验与分析

实验场地为青岛市某处双向四车道，在天桥一侧和车辆前方分别安装毫米波雷达。图8、9分别是实验场地和雷达安装位置。实验主要从准确度和算法效率2个方面来对提出的算法进行可行性验证。为了验证数据配准和滤波算法的准确性，需要将车辆估计位置和速度与车辆真实坐标和行驶速度进行对比分析。通过在车辆上放置高精度GPS定位设备和OBD读取设备来采集这两类真实值。图10是高精度定位和OBD读取设备安装位置图。

图8 实验场地图

图9 路侧和车载雷达安置图

图10 OBD读取设备和高精度定位安装示意图

考虑到占用对向车道超车的实验工况危险性和特殊性，利用同向车道前方车辆换道行为进行相似性实验分析，具体工况如下：自车在右侧道路以5 m/s的速度匀速行驶，左侧车道车辆以同样速度匀速行驶，前车以初始速度为5 m/s在自车正前方匀加速行驶，并在横向距离超过左侧车辆时加速换道。具体行驶工况见图11。在该测试场景中，自车的雷达检测会在前车换道后形成视野受限。

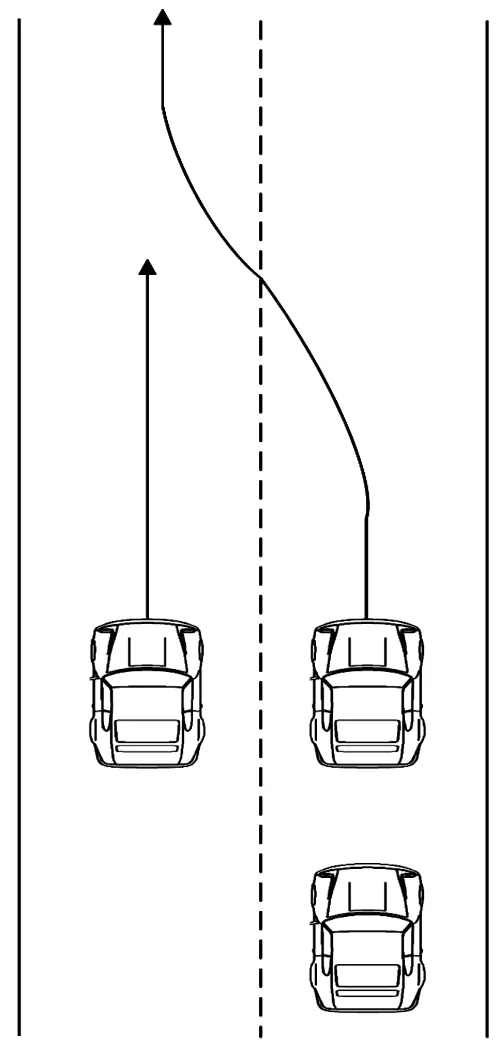
图11 行驶工况示意图

在常用的目标跟踪算法中，普通卡尔曼滤波不适用于非线性系统，而扩展卡尔曼滤波(EKF)是目前应用于非线性状态估计系统中最广泛和最先进的算法。因此，在同一实验工况下，选取EKF算法与本文算法进行对比实验。通过GPS和OBD采集设备得到车辆的真实数据作为结果验证。图12是将本文算法分别运用在车路协同下双传感器融合后的数据，以及单自车车载雷达后，经过多次重复实验，分别在横向距离、纵向距离和速度3个方面的均值估计和误差。

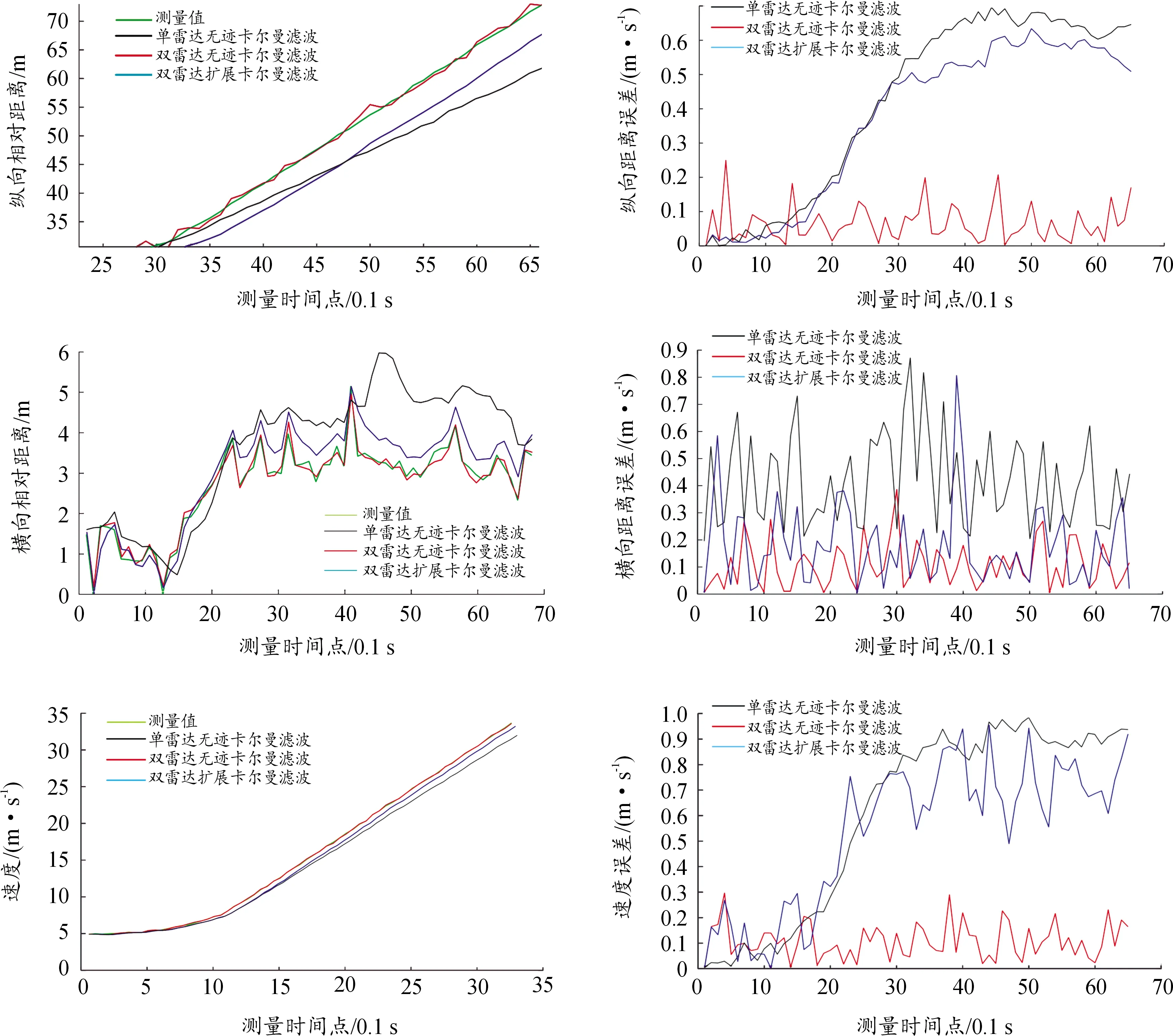
图12 EKF和本文算法的实验结果

根据数理统计知识，均方误差(mean-square error，MSE)是反映预测值与被预测值之间差异程度的一种度量，可以有效地反映预测模型是否具有良好的精确度，其数值越小表示预测精确度越高。表1展示了EKF算法和单雷达与双雷达利用本文算法在多个方面的均方误差。由于车辆换到邻近车道，横向行驶距离相比纵向行驶距离过小，均方误差差距不大；纵向距离和速度上，在利用双雷达融合后数据基础上，本文算法相比EKF算法的均方误差降低了65%以上，验证了所提出车辆跟踪算法的精确性，且双雷达数据相比单一雷达数据在精确性方面提高了70%左右。

表1 2种算法的均方误差 ‰

在算法效率方面，采用通过修正估计值达到稳定线的时间来作为验证指标。图13为3种不同算法和数据集的修正时间以及准确率折线图，其中虚线为经过一定步长后，预测误差达到的稳定线，点划线为达到稳定线所使用的时间点。由图12、13可得，将无迹卡尔曼滤波运用在车路协同下的双雷达融合中可以有效提高车辆识别的精确性和效率。

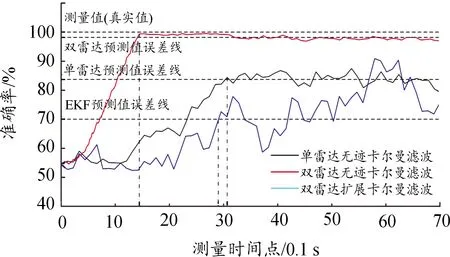
图13 3种预测值的误差稳定图

4 结论

提出了车载和路侧双毫米波雷达数据融合的无迹卡尔曼滤波算法，用于对前方车辆的行驶距离和速度进行检测和跟踪，并通过实车实验对算法进行对比验证，证明车路协同下的双雷达无迹卡尔曼滤波算法在道路视野受限的情况下可有效提高自车对于周围路况的掌握，便于由此展开相关决策研究。但在雷达数据处理方面，如何提高聚类效果并更有效地提取车辆坐标点有待进一步探究。