某SUV行李架的降阻降噪协同优化
赖晨光,贾 浩,付 航,凌志伟,周毓婷
(重庆理工大学 a.汽车零部件先进制造技术教育部重点实验室;b.车辆工程学院,重庆 400054)
在日渐成熟的中国汽车消费市场中,SUV、MPV等车型深受消费者的喜爱,迅速发展持续热卖,车顶行李架已成为SUV、MPV等车型的标准配件。尽管行李架最初的功能是承载重物,但现在更像是配合整个汽车造型的不可缺少的装饰。在汽车行驶过程中,行李架不仅产生气动阻力增加整车的油耗,而且产生气动噪声,尤其是在天窗开启时,对驾驶员和乘客带来很大影响。
由于车顶行李架暴露在高速气流中,而它的横杆的截面形状类似于圆柱和方柱,当高速气流流经行李架横杆时,在其尾部形成交替性的漩涡,导致垂直于流动方向向上的阻力和升力发生剧烈的变化,同时由于交替的涡脱落会产生压力脉动,从而产生风鸣噪声,人长期处于这种噪声状态下会产生烦躁不适的感觉。因此,合理的行李架外形结构研究分析可降低阻力,节省燃油,提高经济性;也可降低气动噪声,改善人体舒适性。
外形对气动阻力与气动噪声影响一直以来是研究工作者研究的重要内容。彭丽娟[1]采用网格变形技术,通过数值仿真的方法对某款SUV改款车的气动阻力进行仿真分析,并对影响气动阻力较大的造型面和气动附件进行了优化;胡之颉[2]通过数值模拟方法研究了主动吹/吸气对气流流经圆柱的影响,并在降噪方面取得一定成就;徐建民等[3]设计了由4个扰流板组成的尾部减阻装置,并详细讨论了底部挡板长度和倾角对气动阻力的减阻作用。但是两者对外形要求达不到统一,而是存在着耦合关系,因此寻找到两者平衡点成了关键问题所在。
近些年来,多学科优化方法成了解决多学科之间耦合问题的热门方法。2004年,在多学科的优化设计过程中,Manning[4]等消除了以前的多学科优化设计中一致模型选择的缺点,提出了一种参数化模型并已成功地用于航天飞机的空气动力学和热传递。2006年,Zarei等[5]基于DOE方法建立了薄管铝柱形碰撞能量吸收的近似模型,实现了薄管铝柱形碰撞能量吸收的多学科优化设计。2019年,Damien Guénot等[6]基于MDO方法利用数值仿真模拟方法,以空客XRF-1运输机作为研究对象,对其机翼、机舱、引擎吊架以及风扇进出口进行了多学科优化设计,并且取得较好的效果。2014年,Yi Feng等[7]利用多学科优化设计对飞行器的气动、气热以及飞行轨迹三个方面进行了优化设计。2016年,湖南大学文琪[8]基于一种将计算流体动力学和优化算法相结合的技术,该技术使用联合优化技术优化排气管结构参数,同时提高了优化效率。 它可以降低阻力并减少由于排气扩散而影响行人呼吸的排气管结构。2018年,张海林[9]基于网格变形技术采用数值仿真模拟的方法来寻找汽车气动阻力的敏感点,通过样本点数据建立设计变量和气动阻力响应关系的响应面模型,并构建协同优化模型进行优化。
综上所述,本研究基于协同优化算法对行李架横杆进行气动阻力与气动噪声2个学科的优化,并取得一定的降阻降噪效果。本文的研究结果作为对汽车降阻降噪以及其他学科间的协同优化具有一定的指导意义。
1 外流场数值仿真方法
以某款加装了行李架的SUV为研究对象,对该SUV进行流场的数值仿真,模拟来流速度为30 m/s时的外流场分布情况。
1.1 CFD数值仿真方法
原始模型是某款SUV的1∶1整车模型,整车车长为4 070 mm,宽为1 990 mm,高为1 650 mm,如图1所示。

图1 原始模型
图2计算域的宽度为车宽的5倍;高度为车高的5倍;长度为车长的11倍,其中计算域入口距离车头3倍车长,车尾距离计算域出口7倍车长。其阻塞比为2.89%,小于5%满足计算要求。气流方向为沿x轴正方向。网格划分策略如图3所示,经网格无关性验证,确定最终网格数量大约为1 347万。

图2 流体计算域

图3 网格策略
对流体计算时,要遵循流体的基本运动规律以及一些准则。基本控制方程表达式为[10]:
1) 连续性微分方程:
(1)
(2)
式中:v、u、w分别对应x、y、z这3个方向上的速度矢量;t为时间;V为速度矢量。
2) 动量方程

(3)
(4)
(5)
式中:p为流体微元体表面所受压力,τxx、τyx、τzx等为流体微团表面所受切应力在各个面各个方向的分量,fx、fy、fz为作用在流体微团上的体积力在3个坐标轴上的分量。
考虑到行李架模型存在气流分离以及边界层的影响,以及来流速度为30 m/s,选用稳态计算模型可实现的k-ε模型,瞬态计算模型为SSTk-ω模型。
1.2 仿真结果
原始模型的阻力值为387.26 N,噪声值为63.48 dB。整车压力云图如图4~6所示,当汽车高速行驶时,高速的气流与整车的前脸相撞击,造成气流在汽车头部的进气格栅部位以及前挡风玻璃处被大量阻塞,气流的流速迅速降低,因此在相应的部位产生了高压区区域。而在进气格栅和引擎盖的交界处以及前挡风玻璃与车顶的交界处,气流发生了严重的分离,迅速将对应部位的气流抽走,而形成了负压区。同时分离的气流与来流又分别在引擎盖和车顶的中部进行交汇并再次附着。随着气流流经整车尾部时,气流又再次分离,在尾流区域形成负压区,因而造成了汽车的气动阻力。在前后杆径向的中部形成了高压区域而在两侧形成了一定的负压区域,产生了压力梯度。

图4 中截面压力云图

图5 行李架压力云图(迎风面)

图6 行李架压力云图(背风面)
图7~9是行李架湍流能量云图。从图7可以看出,在前杆和后杆的尾部产生交替的湍流能量团。从图8来看,前杆产生的湍流能量主要集中在前杆的上下两侧以及尾部。而从图9可以看出,后杆产生的湍流能量主要集中在后杆的头部。产生这些湍流能量主要原因是气流在流经固体表面时没有很好的附着,产生了分离从而导致了涡流。这些涡流的产生和发展本质上是一种能量损耗,表现为汽车气动阻力的增大,最终体现为燃油消耗的增加。

图7 行李架湍流能量云图(俯视图)

图8 行李架前杆湍流能量云图

图9 行李架后杆湍流能量云图
图10、11分别是Curle声功率云图与Proudman声功率云图。湍流场的 Curle 声功率模型会计算偶极源产生的声源(83~104 dB)。可以看出,行李架杆前端会产生较强的偶极子声源。主要噪声源集中在迎风面的边缘处。这些噪声源都与杆造成的流场密切相关。Proudman宽频噪声预测模型主要用于预测汽车高速行驶时的四极子声源(70~90 dB)。通过图中可以看出,其具体噪声源部位与偶极子相似,也是因为气流分离引起的。通过以上分析得知,汽车在高速行驶时主要以偶极子为主,四极子为辅。
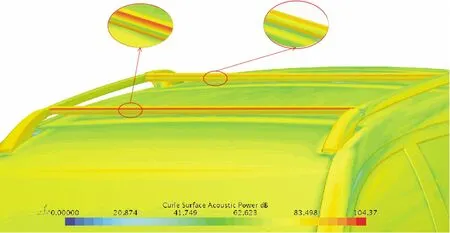
图10 Curle声功率云图

图11 Proudman声功率云图
本文中研究远场噪声,应用工程上监测杆件的远场常用布置方法如图12所示。以两杆中心为原心,以4 m为半径,每隔18°取1个监测点,建立11个远场噪声检测点,利用FW-H方程计算远场发声情况。

图12 噪声监测点分布
为了忽略后视镜、引擎盖等其他噪声源的影响,单独对行李架产生的远场噪声进行监测。利用FW-H方程求解流场传到11个监测点在时域下的脉动压力数值,通过傅里叶快速变化转换成频域下的脉动压力,同时根据用声压级计算方法最终得到11个监测点声压级频谱曲线,如图13所示。可以更加清晰地对各个监测点的噪声水平进行对比分析。行李架杆在低频(0~400 Hz)和高频(4 400~5 000 Hz)的声压级较高,在2 200~2 800 Hz频率时有出现另一峰值的迹象,通过与无行李架原车模型对比,在该频段时,原车模型是有一个峰值的,但是由于行李架存在的原因使该峰值被降低。并且各个点的声压级频谱曲线走向趋势都是一致的,但是第6个监测点曲线明显比其他监测点高一些,为了更好地确定这种现象,所以将11个监测点的数据信息导出,用Matlab软件对各监测点的总声压级进行计算,得出各个监测点总声压级值如表1所示。

图13 监测点声压级频谱曲线

表1 11个监测点的声压级值
1.3 优化设计变量的选取
根据前面对原始模型的稳态计算和瞬态计算结果的分析,原始模型行李架杆产生较大噪音和阻力的原因可能有以下几个方面:
1) 杆前端的倒角度过大,导致高速气流正面垂直冲击行李架杆的面积较大,造成过多的气流阻塞,同时还使边缘处因为连贯性不强导致气流附着困难而引起此处气流流速较快,行李架后方横向有较大速度差产生较大湍流,成为噪声与阻力源。
2) 杆后端的倒角度过大,导致此处气流分离严重,而且使气流过早分离后,尾流区面较大,不利于气流恢复,并使杆尾流区域产生湍流和较大涡旋,成为噪声和阻力源。
3) 前杆对后杆的气流影响,由于两杆串联,前杆产生的气流造成通过后杆的气流不稳定,而产生一定的速度差,从而导致后杆湍流和涡旋加大。
综上所述,同时考虑到在优化过程中不能对行李架的主要功能造成影响,即一定程度不改变其力学性能而导致其承载能力发生改变,所以在不改变最大厚度dmax情况下,设计了4个优化设计变量,即前杆的前后2个倒角半径R1、R2和后杆的前后2个倒角R3、R4。根据国家强制性标准(GB 20182—2006)外凸物半径不小于2.5 mm,所以确定优化设计变量R范围在3~10 mm,如图14所示。

图14 行李架杆的优化设计变量
2 气动阻力与气动噪声的单目标优化
根据Kriging近似模型的建模要求,最优拉丁超立方采样时至少需要选取10n+1个(n是变量个数)样本点,获取41组样本点[11]。基于网格变形技术,建立样本点模型并进行仿真计算。然后利用样本点数据分别建立阻力与噪声Kriging近似模型以及分别利用决定系数R2方法验证模型的精度,如图15、16所示[12-14]。阻力样本点的近似模型R2=0.909 51,噪声样本点的近似模型R2=0.933 95,R2值均在0.9以上,故近似模型满足计算要求。基于阻力与噪声模型近似模型,利用多岛遗传算法[15]分别对阻力和噪声进行单目标优化。
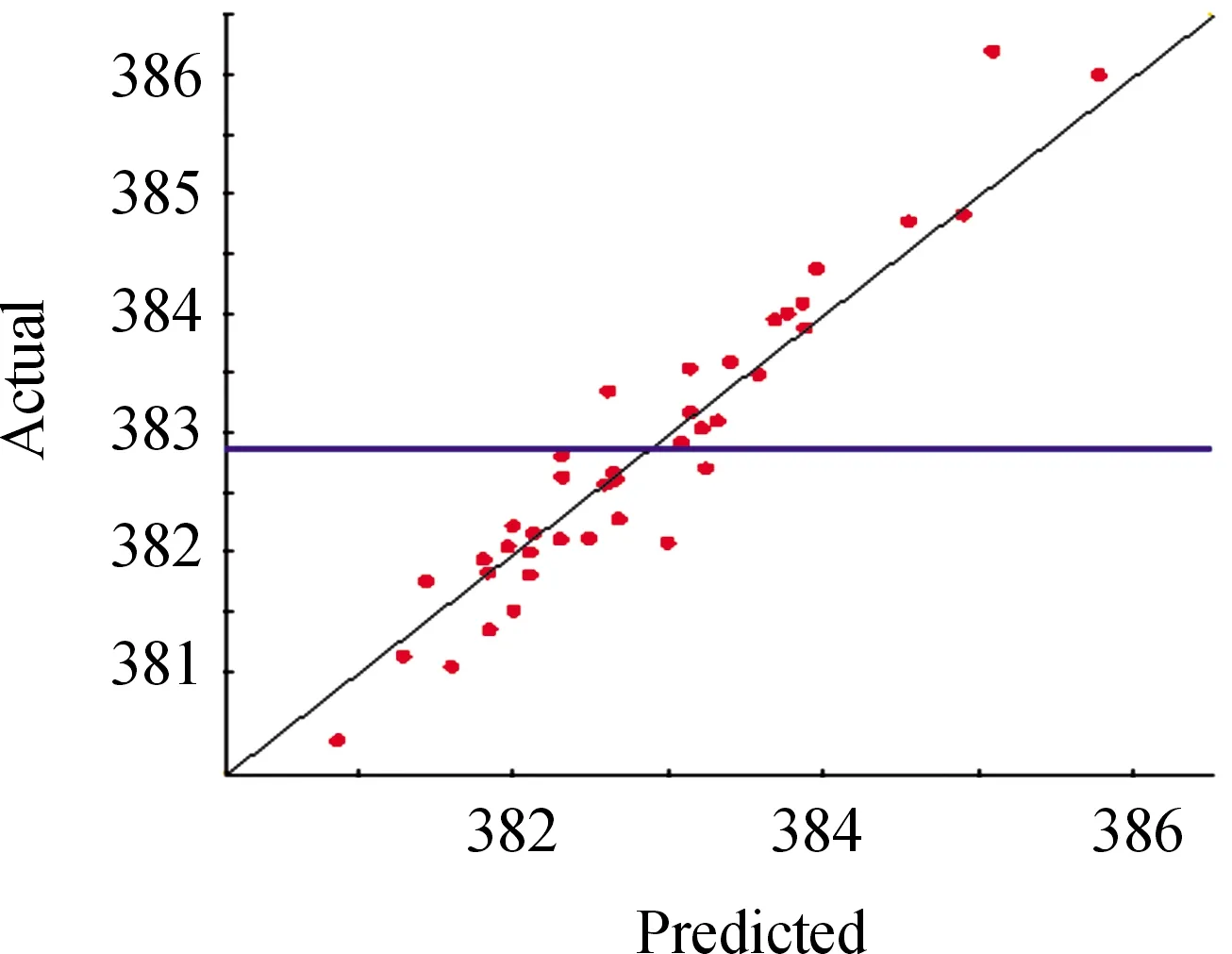
图15 阻力散点图

图16 噪声散点图
2.1 气动阻力的单目标优化
通过仿真得到阻力最优模型的仿真值为380.45 N,降低了1.76%(网格精度为0.103%),与算法预测值的误差为0.263%,故该结果具有可靠性。
图17是原始模型和阻力最优模型的压力云图。通过对比可以发现,原始模型中行李架横杆的径向中部代表高压区的深红色区域经过优化后对应的位置颜色变成了浅红色,而代表着负压区域的深蓝色也变成了浅蓝色。说明阻力最优模型相对于原始模型来说,其高压区的压力明显降低,而负压区的负压值也变小了,即行李架横杆表面的压差较低角度,优化前后的压力恢复明显变好,从而压差阻力也会有所降低。

图17 原始模型与阻力最优模型压力云图
图18、19分别是原始模型与阻力最优模型的速度矢量云图。结合图17(a)与(b),前杆尾流区的“死水区”面积经优化后明显减小,同时尾部的涡旋也较小。同时前杆头部边缘由于气流分离产生的高速气流也得到明显的改善。

图18 前杆速度矢量卷积分云图

图19 后杆速度矢量卷积分云图
通过图18(a)与(b)可看到,后杆尾流区的“死水区”面积经优化后大幅度减少,尾部的2个较大涡也变成了较小涡旋。究其原因是行李架的前端倒角与后端倒角改变后,在杆前端头部变得相对尖锐,正面而来的高速气流不会过多地垂直冲击在头部上而引起气流阻滞,而边缘处相对圆滑,使气流流经时转折度较小,附着性更强,不会引发更多的气流分离。同理,尾部的边缘处也相对圆滑,气流附着性好,不会过早地形成气流分离,使尾流区域的“死水区”面积降低,这利于尾流区域的气流恢复。涡旋变小和气流分离状况得到改善,都说明行李架周围的湍流强度降低,这也减小了能量的耗散,从而降低了整车动能的损失。
2.2 气动噪声的单目标优化
通过仿真得到噪声最优模型的仿真值为53.71 dB,降低了15.39%,与算法预测值的误差为3.07%,小于5%,故该结果具有可靠性。
图20是原始模型和噪声最优模型的Curle声功率云图。通过Curle声功率云图对比可以看出,前杆的深红色区域有明显的变浅,但是红色面积有所增加,说明噪声的声压强度有了一定的减弱,但是噪声源区域相对来说增多了一点。对于后杆来说,无论是代表声压强度的颜色深度还是代表噪声源的红色面积都有所降低。总体来说对噪声都是靠向减弱方面。根据噪声的产生机理,由于行李架横杆的倒角半径发生改变后,使气流附着在杆件表面变得容易了些,即气流分离得到了一定的抑制,从而压力变化不大。

图20 Curle声功率云图
从图21可以看出,在优化前后,在气流流动方向上两杆尾部交替产生湍流能量明显减少,使尾流区域的湍流状况得到了明显改善,湍流能量的减少代表着尾流区域的湍流强度减弱。

图21 湍流能量云图
3 协同优化
在建立协同优化模型的系统级优化器之前,要根据不同子学科的不同要求对各自进行分配权重,结合第四章单目标优化结果发现噪声的优化空间较大一些,所以设置了阻力与噪声权重比为 5∶5、4∶6、3∶7、2∶8,即在协同优化时对权重大的子学科优化占比会更高一点。
3.1 建立协同优化数学模型
系统级优化目标数学表达式:
MinS=A(F-379.65)+B(SPL-52.06)
(6)
式中:A为阻力权重;B为噪声权重;F为阻力学科传递给系统的优化值;SPL为噪声学科传递给系统的优化值。
系统级优化器数学模型:
S1=(x1s-x2l)2+(x2s-x2l)2+(x3s-x3l)2+
(x4s-x4l)2+(SPLs-SPLb)2
(7)
S2=(x1s-x2l)2+(x2s-x2l)2+(x3s-x3l)2+
(x4s-x4l)2+(Fs-Fb)2
(8)
式中:x1s、x2s、x3s、x4s为系统级的设计变量;x1l、x2l、x3l、x4l为学科级优化后传递给系统级的设计变量;SPLb、Fb为子学科传递给系统级的噪声、阻力优化值;SPLs、Fs为系统期望值S1≤0.001,S2≤0.001。
气动阻力子学科优化器数学模型:
Min:d2=(x1s-x1b)2+(x2s-x2b)2+
(x3s-x3b)2+(x4s-x4b)2+
(Fs-Fb)2
(9)
气动噪声子学科优化器数学模型:
Min:d1=(x1s-x1b)2+(x2s-x2b)2+
(x3s-x3b)2+(x4s-x4b)2+
(SPLs-SPLb)2
(10)
式中:x1b、x2b、x3b、x4b为4个变量值;SPLb、Fb为子学科的噪声、阻力优化值;SPLs、Fs为系统期望值;d1、d2分别为噪声和阻力学科耦合变量和共享变量的差异。
3.2 协同优化流程
图22是协同优化基本结构框图,最上层框图为低阻低噪的系统级优化器,其系统优化目标为根据一定权重比下,气动阻力和气动噪声在优化设计变量范围内分别与它们自身差值之和最小值。下面2个框图分别为阻力学科和噪声学科的子系统优化器,它们各自有着自身的学科自约束条件。利用Isight软件对上节建立的协同优化算法数学模型进行搭建,如图23所示。

图22 协同优化基本结构框图

图23 协同优化流程框图
3.3 协同优化结果
共设置4种不同阻力与噪声权重比下的协同优化,得到4组协同优化结果,如表2所示。通过对比4组协同优化结果,随着噪声占比权重加大,噪声降低的幅度逐渐减小。因为噪声变化不大,为了更多地降低阻力,故选用4∶6的权重比作为最终优化结果并在后面做验证仿真分析。结果如表3所示。

表2 协同优化结果

表3 预测值与仿真值结果
流场的压力云图一般最能够直观反映阻力变化,因此从整车的压力云图来看,如图24所示,整车周围的压力分布没有随着行李架外形的改变而大幅度改变,符合汽车空气动力学的一般规律。但是如标记所示在尾流区域负压为82.65 Pa的区域面积明显减少,这就说明优化后的模型尾流区域的压差有所降低,对压差阻力恢复是有利的,也是整车阻力降低的原因。

图24 整车压力云图
如图25所示,从行李架横杆本身分析,优化后无论是代表高压区的红色面积还是代表负压区的绿色面积都缩小了,并且对应的颜色也变浅了,说明优化模型行李架杆表面的压力差减小了,其本质是气流在行李架杆表面的阻塞和分离降低了,这都对降低阻力以及减少压力脉动起到重要作用。

图25 行李架横杆压力云图
通过声压级频谱曲线图可以较为直观的看出优化前后的噪声声压级的变化,如图26所示,从图中可以对比出,协同优化出来的低阻低噪模型声压级频谱曲线基本都处于原始模型曲线的下方,其最大峰值与噪声大小水平均小于原始模型,噪声得到了明显的降低。

图26 声压级频谱曲线
4 结论
1) 行李架两横杆的前后端的气流阻塞以及气流分离是造成压差阻力、湍流强度以及脉动压力的主要原因。行李架产生的噪声源以偶极子声源为主,四极子声源为辅。行李架横杆靠近车顶而产生的近壁效应对流场的影响也较大,车顶对行李架杆下部气流有压缩的作用,导致杆尾流区域面积增大;行李架的存在也会影响车顶气流的附着,对整车尾流也会产生一定影响。
2) 通过对整车模型阻力和噪声进行单目标寻优,得到阻力单目标优化值为379.65 N,降低了1.97%,噪声单目标优化值52.06 dB,降低了17.99%。
3) 通过建立协同优化算法数学模型,并计算4种不同权重比下的协同优化模型,最终确立阻力与噪声比为4∶6的一组作为最终优化结果。在对协同优化预测模型进行了仿真验证后,得到了阻力最终优化值为381.08 N,降低了1.60%,预测值与仿真值误差为0.17%;噪声最终优化值为54.01 dB,降低了14.92%,预测值与仿真值误差为3.67%。

