对与自由电子相关联的一些问题的梳理及教学建议——以金属导体为例

蒋炜波

(清华大学附属中学 北京 100084)

赵 坚

(昆明市五华区基础教育发展研究院 云南 昆明 650031)

1 引言

与导体中的自由电子相关联的一些物理问题，在高中物理中很常见，比如图1所示，固定于水平面的导杆MN和PQ处于竖直向下的匀强磁场B中，金属直导线ab在安培力的作用下向右运动.在这一情景中，导体中的自由电子会受到磁场、电场、金属离子(晶格)等施加的各种作用力，这类问题往往涉及到宏观和微观之间的联系，因此一直是学生学习理解和教师教学过程中的一大难点.但受限于中学阶段的学习和教学要求，教材并未对这些作用力进行系统的分析阐述，同时从物理课程的新要求看，《普通高中物理课程标准(2017年版)》明确提出将“物理观念、科学思维、科学探究、科学态度与责任”4个方面作为物理学科的核心素养要求.鉴于此，有必要对金属导体中与自由电子相关联的一些中学教学范畴内的问题，做出梳理探讨，并提出相应的教学建议，供大家教学中参考.

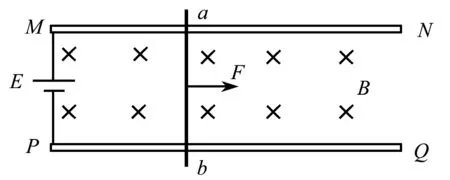
图1 通电导体在磁场中受力

2 自由电子

什么是金属导体中的自由电子呢？按照经典原子核式结构理论和能级理论，原子核周围存在着绕核运行的电子，这些电子分别位于不同的能级上，所处能级越高，电子越容易脱离原子核的束缚，但脱离的过程仍然需要克服原子核的束缚作用做功.对单个金属原子而言，电子都处于束缚状态，没有自由电子的概念，但是对于由金属原子构成的宏观导体而言，情况则有所不同.

2.1 金属键

在金属导体中，大量的原子规则地排列在一起，对于单个原子，其能带和能级精细结构如图2所示，电子只能处于某一个能带的某一精细能级上.那么金属导体就相当于将这些能带势阱有规则地排列在一起，因此必然带来能级的重叠，此时原子之间“共用”了较高的能级，而原本在这些能级上的电子便可以在这些金属原子之间自由移动，如图3所示，这些电子属于整个金属导体所共有.相比于分子内共用电子对的化学键而言，金属导体中的共用电子数量异常庞大，它们最终将金属导体中的所有金属原子联系在一起，形成了类似于化学键的庞大的金属键网络，所以金属导体整体上就相当于一个超级庞大的分子.

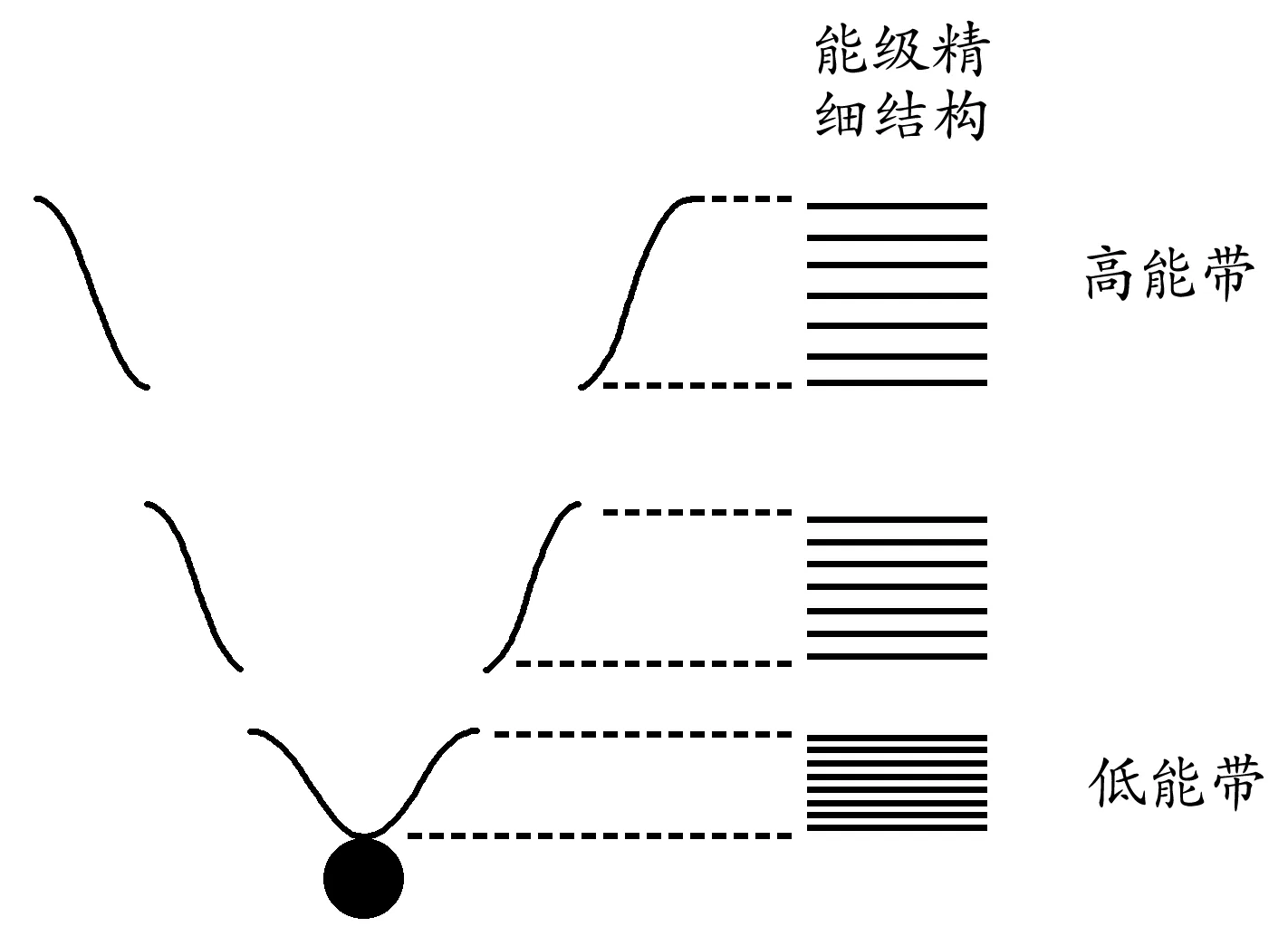
图2 原子能级

图3 金属键网络示意图

2.2 自由电子导电

原子之间共用能级形成金属键网络以后，原本处在这些被共用的能级上的电子，就可以在不同的原子之间转移，这样的电子就是自由电子.可见，自由电子并不是真的自由，它只是能够在原子共用的能级轨道上移动，整体上看仍然受到原子的束缚作用，只不过由于可以在整个导体内部移动，因此自由电子能够很好地参与导电.

一般而言，金属导体中自由电子的数量越多，导电能力越强，但是通常情况下，金属原子只能共用外层高能级形成金属键，因而导电能力有限.如果能够进一步重叠原子的能级，让更多的次外层能级也在原子之间共用，那么就能够形成更多的金属键网络，让更多的电子参与导电，从而提高金属的导电性能.

2.3 自由电子的运动

如果导体外界没有任何电磁场或者其他原因(比如温度不均匀、电子数密度差等)的干扰，那么这些自由电子将在导体中无规则地运动，自由电子之间，以及自由电子与金属晶体的晶格之间，都在不停的碰撞，因此自由电子的运动特征与理想气体分子的运动类似，故称为自由电子气体[1].自由电子无规则运动的速度非常快，其数量级在105m/s，但是由于不是定向移动，因此无法直接形成电流.

2.4 教学建议

目前的中学物理教学中，对于自由电子的阐述很少，新版高中物理教材在必修3中虽然阐述了金属导体中自由电子定向移动形成电流的微观情景，并给出了电子定向移动的数量级[2]，但是仍然没有简明扼要地解释什么是自由电子.

在高中阶段的原子物理部分，还将涉及到光电效应、康普顿散射等与电子相关的内容，学生经常困惑于一些问题，比如光电效应中逸出的电子来源于什么地方呢？是金属中的自由电子还是更低能级的束缚电子？康普顿散射针对的是金属导体中的自由电子吗？想要帮助学生明确解答这些疑惑，教学过程中就需要教师一是做到心中有数，二是结合教学实际，适当帮助学生形成物理观念和科学思维，初步建构起金属中的电子运动模型，让学生对导体中的自由电子、非自由电子和逸出导体外的真正自由电子能够有所区分.

3 电流的形成

如果在导体两端施加电压，导体中就会建立起电场，自由电子在电场力的作用下，将会在无规则运动的同时(可以证明，从宏观总体来看，自由电子的热运动对电流的贡献几乎没有)，向着电场的反方向定向移动，从而形成电流.

3.1 自由电子所受电场力

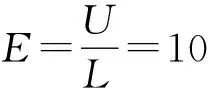
另一方面，导体中的自由电子数量很多，因此所有自由电子所受电场力的总和也非常大.仍以上述铜导线为例，其单位体积的自由电子数n=8.4×1028个/m3，故而自由电子的总数N=nSL=8.4×1021个，于是可计算出自由电子所受电场力之和达到了惊人的F=nSLEe=UnSe=1.34×104N.

对于这一电场力的计算公式，还可以从做功的角度进行分析.比如电流做功产生热量，本质上是电场力推动自由电荷定向移动做功，再由自由电荷与晶格碰撞增加原子不规则运动的剧烈程度，从而让导体的温度升高，内能增大.我们知道电流做功表达式为W=UIt，而在t时间内，自由电子定向移动距离s=vt，于是利用电流微观表达式I=neSv，能够得到所有自由电子所受电场力为

可见，自由电子所受的如此大的电场力，与宏观上电流做功是相吻合的.

3.2 晶格所受电场力

与自由电子相对应，金属晶体的晶格带正电，带电总量与自由电子带电总量相同.既然自由电子受到了很大的电场力，那么带正电的晶格也不能例外.比如在上述铜导线例子中，显然晶格受到的电场力也应该是F=1.34×104N.但是如此大的电场力作用在晶格上，我们为什么看不到金属铜导线沿着电场方向直接移动呢？而且现实中也并不需要对金属铜导线施加一个很大的力以抵消其所受的电场力，从而维持导线的静止状态，这又是为什么呢？

究其原因，乃是自由电子与晶格之间的碰撞所致.不考虑金属铜导线受到的其他外界作用力，在上述电场作用下，金属铜导线整体上动量守恒，如果自由电子与晶格之间不发生碰撞，那么自由电子的运动速度将会非常大，而金属铜导线也会由于晶格所受的巨大的电场力作用难以保持静止.正是由于金属铜导线内部电子和晶格的不断碰撞，使得自由电子定向移动的速度很小，仅仅为10-5m/s数量级，而金属铜导线的晶格质量远远大于自由电子的质量，利用动量守恒不难算出金属铜导线的定向移动速度仅仅为10-12m/s数量级，因此在宏观上完全可以忽略不计.

所以在处理相关这类问题的时候，我们可以近似认为自由电子与晶格之间的平均碰撞内力作用与自由电子所受电场力一样大，这样晶格所受电场力和碰撞作用力相平衡，因此现实中不需要再给金属导体施加一个力来维持其静止状态.

3.3 电流的大小

自由电子在电场力作用下定向移动时，由于伴随着电子的无规则热运动，因此碰撞将非常频繁.金属铜原子的直径数量级为10-10m，自由电子无规则运动时两次碰撞的距离间隔必然小于铜原子的直径，近似数量级取为10-11m，自由电子热运动的速度数量级为105m/s，由此可计算出自由电子两次碰撞之间的时间间隔数量级为10-16s，再借助上述分析过程求出的自由电子在电场力作用下的加速度数量级1012m/s2，不难得到在这段碰撞时间内，自由电子依靠电场力加速得到的定向移动的平均速度数量级仅为10-5m/s.

如果取碰撞时间间隔为T，电子加速度为a，导线长度为L，导线横截面积为S，导线两端电压为U，电子质量为m，电子电荷量为e，单位体积自由电子数为n.于是得到电子运动的加速度为

电子定向移动的平均速度为

由电流I=neSv可得电流表达式为

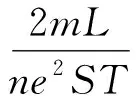
这正是部分电路欧姆定律表达式.对于更一般的情形，可以将电阻R表示为

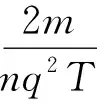
可见，这便是电阻定律表达式.

3.4 教学建议

在物理学习中，学生会对电流做功和力学中力做功产生困惑，其实二者从本质上看并没有什么不同，教学中可以从微观角度帮助学生建构电场力推动电荷做功的情境，从而将力学和电学中的做功衔接贯通，真正将功和能的物理观念建立起来.

与此同时，通常的教学中只会考虑自由电子在电场中受力运动，很少会去思考带正电的晶格所受的电场力，通常即使知道自由电子会与晶格反复碰撞，也不会过多去思考晶格被碰撞后会如何运动的问题.这都是因为教学中对电流的微观过程涉及过少，没有能够真正建立起欧姆定律的微观情境所导致的.

所以，教学中适当引导学生将宏观和微观联系起来建构模型，从而有机地将欧姆定律、电阻定律、电场力、加速、碰撞等元素进行整合，这对学生科学思维的培养将是非常有益的.

4 安培力的产生机制

运动的电荷在磁场中受到洛伦兹力的作用，而导体中的电流是由自由电荷定向移动形成的，可是电流在磁场中受到的却是安培力，安培力与洛伦兹力有什么关系呢？教学中部分教师通常解释为“安培力是洛伦兹力的宏观表现，每一个定向移动的自由电荷所受到的洛伦兹力的总和就是安培力”，但这种解释比较宏观和含糊，也容易产生疑议.比如当通电金属导体在磁场中运动的时候，自由电子还会受到沿导体方向的洛伦兹力，显然这时候自由电子所受洛伦兹力的总和并不是安培力.再者，金属导体由自由电子和晶格组成，讨论安培力的时候，只分析质量微乎其微的定向移动的电子，而不分析质量占绝大部分的晶格，这显然也是不合适的.鉴于此，我们有必要从微观角度对安培力的产生机制作出分析说明.

4.1 通电导体在磁场中运动时出现的霍尔场

如图4所示，通电导体ab静止在垂直于纸面向里的匀强磁场之中，ab的横截面积为S，磁场中的长度为L，单位体积自由电荷数为n，此时内部定向移动的自由电子受到的洛伦兹力向右，于是导体的右表面聚集负电荷，左表面聚集起相对应的正电荷，从而建立起向右的电场(霍尔场)，向右的电场会对定向移动的电子施加向左的电场力.电子会不断地在洛伦兹力的作用下向右聚集，从而不断地增强内部的电场强度，直到导体内部自由电子所受的洛伦兹力和电场力相平衡为止，此现象称为霍尔效应.此后，自由电子不再向右聚集，而是一直沿导体向上定向运动.

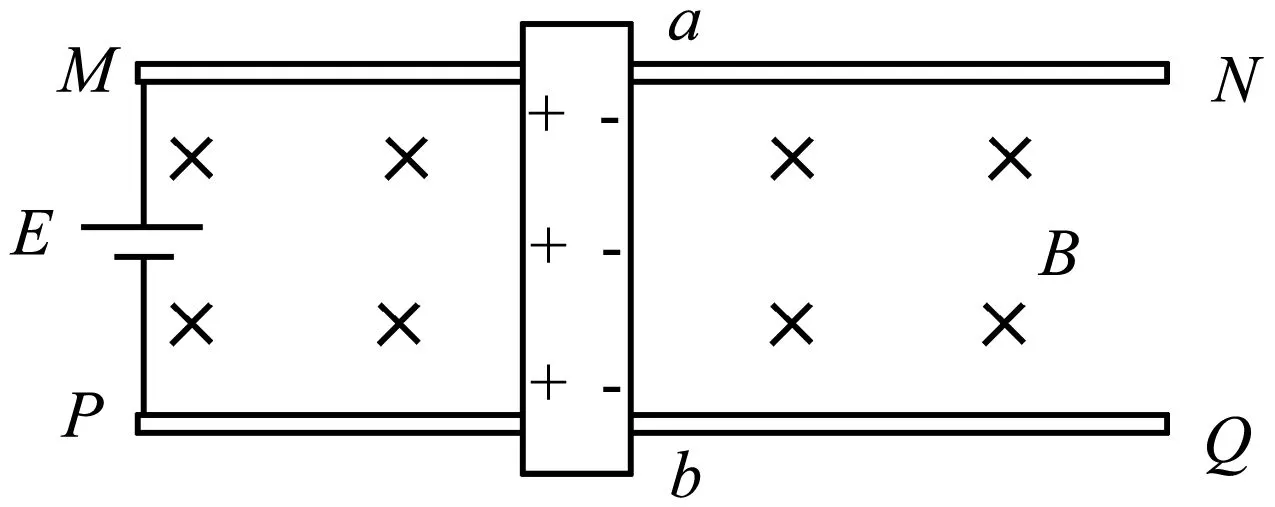
图4 通电导体内的霍尔效应

可见，由于霍尔效应的出现，导体被分成了4部分：右侧表面聚集的自由电子、左侧表面与这部分自由电子相对应的晶格、导体内部的其他自由电子和以之相对应的导体内部的晶格，因此对通电导体在磁场中运动时所受安培力的探讨分析，首先需要清楚和明确这4部分的受力以及它们之间所受力的彼此关系.

4.2 安培力的本质

为了分析的方便，不妨先将导体ab分为如图5所示的两大部分：第1部分是在导体内部形成霍尔电场后，导体内部定向移动的电子和与之相对应的静止的晶格，第2部分则是处于导体右侧表面聚集的在电源提供的电场力作用下做定向移动的电子和与其相对应的左侧表面静止的晶格.

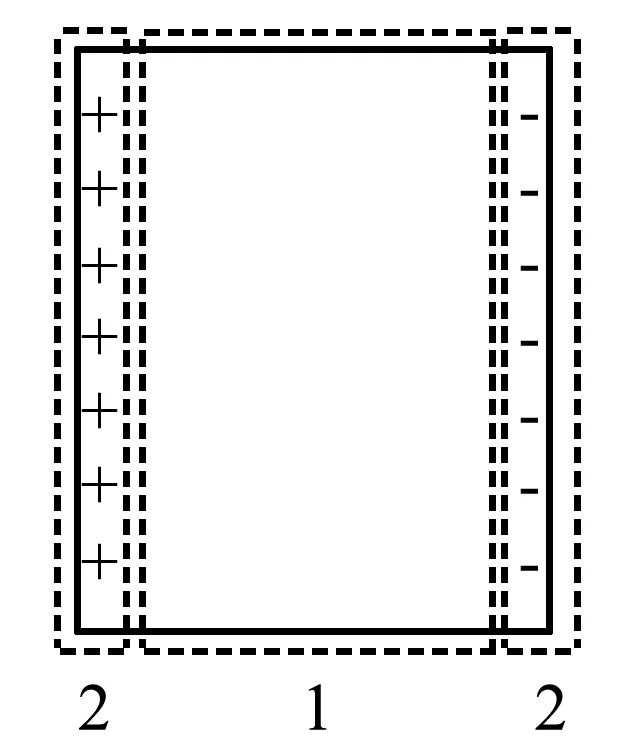
图5 导体划分

对第1部分进行受力分析，如图6所示，F洛1是外磁场对导体内部做定向移动的电子施加的洛伦兹力，F1是霍尔效应产生的电场对导体内部定向移动电子的电场力，F2是霍尔效应产生的电场对导体内部晶格的电场力.

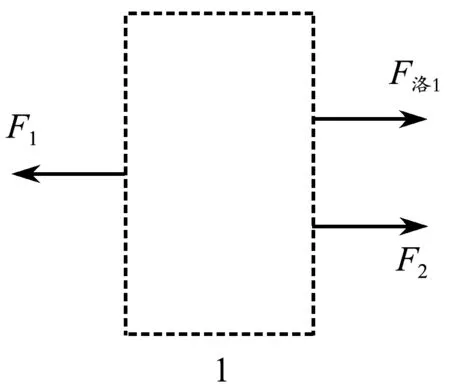
图6 第1部分受力

对第2部分进行受力分析，如图7所示，F洛2是外磁场对聚集在导体右表面在电源提供的电场力作用下做定向移动的电子产生的洛伦兹力.而由于霍尔效应产生的电场对导体内部定向移动的电子存在电场力F1，因此这些定向移动的电子也会对第2部分整体产生一个反作用力，即F3.同时，霍尔效应产生的电场对导体内部的晶格存在电场力F2，因此晶格也会对第2部分产生一个反作用力，即F4.此外，由于导体右表面聚集了电子，金属导体还会对这些电子有额外的束缚作用(否则电子会逸出导线)，因此第2部分还会受到一个束缚作用力F5.

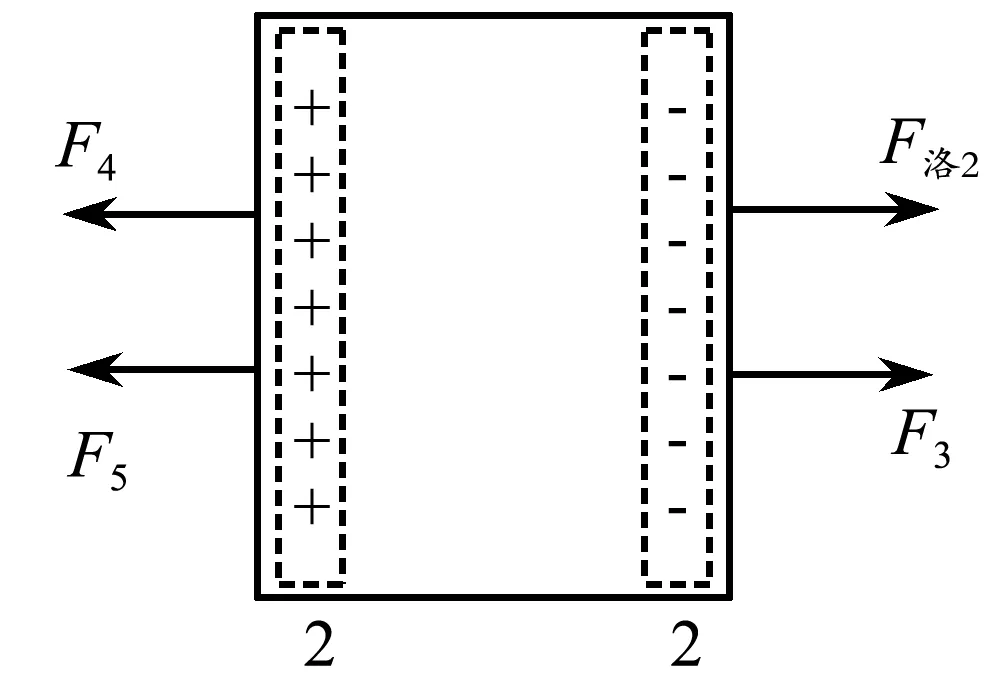
图7 第二部分整体受力

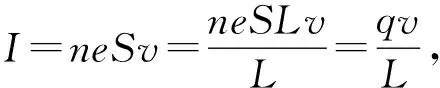
另外，在图4中，作为金属导体中的自由电子来说，在通电导体向右运动起来后，也将会随通电导体参与其运动，因此自由电子也必然会受到外磁场对它施加的洛伦兹力作用，但由于此时这些电子所受的洛伦兹力并不垂直于导线，而是沿着导线从a指向b，其作用是阻碍电子在电场力作用下从b到a的定向移动(即电磁感应产生反电动势)，故而对宏观的安培力没有贡献，不用考虑.

所以，为了避免通电导体运动起来后，其所受到的安培力与它内部的自由电子受到的洛伦兹力在认识上带来的误区，我们不妨可以将“通电导体中定向移动的自由电荷(包括内部和表面)所受洛伦兹力沿垂直于导体方向的分力的总贡献”称为安培力.

那么作用在定向移动的自由电子上的安培力，又是如何让导体整体受力运动的呢？这就要分析金属导体中带正电的晶格的受力了.

4.3 晶格的受力

目前对于晶格受力，有两种主要的解释.第一种是在导体内部定向移动的自由电子会受到外部磁场施加的洛伦兹力，如图4所示，自由电子会向右侧表面运动聚集，在运动聚集过程中将与晶格发生连续碰撞，从而对晶格产生作用力[1]，因而宏观上看起来是金属导体本身受到这个力.这一“碰撞传递冲量”观点一直是学术界的主流观点.第二种则认为由于定向移动的自由电子向右侧表面聚集后，会建立起霍尔电场，霍尔电场对内部自由电子有作用力，自然也会对晶格产生作用力[3].

这两种观点在晶格的处理上是一致的，即认可安培力是洛伦兹力的一种宏观体现，自由电子需要通过对晶格施加作用力从而带动金属导体受力运动，这里进一步从微观角度进行阐述.如图5所示，霍尔效应产生的电场，对导体内部晶格也有向右的电场力作用，假设电场强度为E，则这一作用力大小为F6=Eq内，而在霍尔电场稳定后E=Bv，于是得到导体内部晶格受到的作用力F6=Bvq内.

进一步考虑到该电场对导体左表面正电晶格向右的电场力，由于电场是右表面负电荷和左表面正电荷共同作用形成的，因此左表面正电荷所处位置的电场强度应该为γE，γ<1，于是其受力F7=γEq表.可见，考虑到电场对左表面晶格的电场力作用后，金属导体所有晶格所受的总电场力大小F电=F6+F7=Bv(q内+γq表) ，与安培力仍然相差(1-γ)Bvq表.

晶格受力所差的这(1-γ)Bvq表，正是金属导体对右侧表面自由电荷的束缚作用力F5的反作用力，如图8所示，即F′5=F5=(1-γ)Bvq表.不妨再直接对右侧表面的自由电子进行分析.

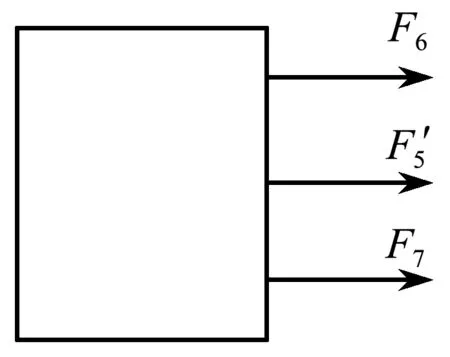
图8 晶格整体受力

如图9所示，右表面电子所受向右的洛伦兹力F洛2=Bvq表，而左表面晶格和右表面电子产生的电场，对右表面电子的向左作用力F8=γEq表=γBvq表，小于右表面电子所受向右的洛伦兹力F洛2，因此从右表面的电子受力平衡进行分析，可以得到金属导体对右表面自由电子的束缚作用力F5=(1-γ)Bvq表，因而右侧表面电子对金属导体存在等大的反作用力F′5，即F′5=(1-γ)Bvq表.

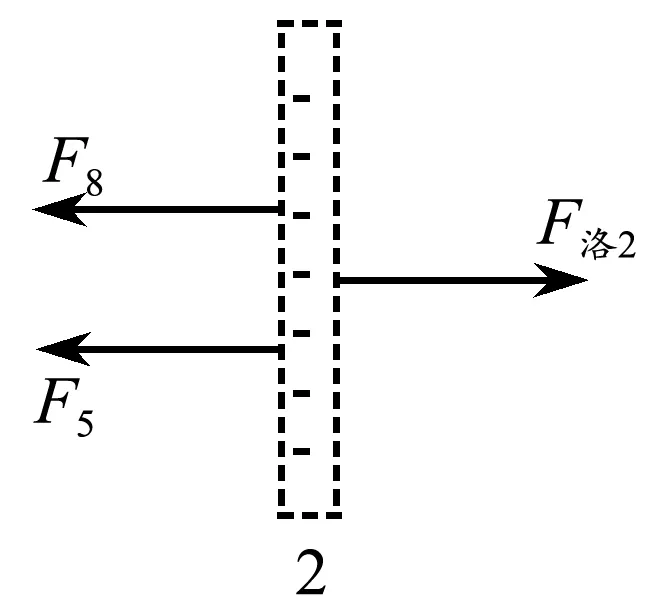
图9 右侧表面电子受力

因此，金属导体晶格所受的力，既包括霍尔效应产生的电场对所有正电晶格的作用力，又包括右侧表面电子所受束缚作用力的反作用力，二者的总和与通电金属导体中对定向移动的电子所受的垂直导线方向的洛伦兹力大小相等，这便是金属导体所受的安培力.

4.4 关于导体表面电子的电荷量

在安培力的产生机制中，自由电子在导线表面聚集程度是否会过大导致电子逸出导线呢？

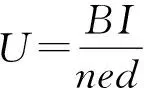
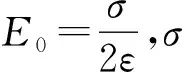
需要说明的是，虽然这一探讨使用了无限大带电平面，这于金属导体(导线)而言并不太恰当，但对于数量级的估算是可取的.

4.5 教学建议

碍于中学阶段的学习要求，教学中我们不可能如此细致地向学生阐述分析安培力的产生机制，但是作为教师应该要做到心中有数，对安培力的一些表述应该做到尽可能地科学规范.比如，将安培力称为自由电子所受的洛伦兹力的合力并不可取，尤其在导体存在切割磁感线运动的时候，这一点已有不少文章进行了讨论[4].教学中我们应该明确，只有沿垂直导体方向的洛伦兹力产生的总的贡献所表现出的宏观效果，才能称为安培力.安培力是由于导体表面和内部的自由电子通过对晶格产生作用力，从而让导体整体上表现为受到安培力的作用.另外，从能量角度来看，洛伦兹力的作用并不提供能量，而只是传递能量，它把来自电源的维持电流恒定的能量转化为载流导体的动能.

5 结束语

宏观和微观之间的联系，原本就是高中物理教学中培养学生物理观念和科学思维的绝佳切入点，而对导体中自由电子受力的辨析，则是更进一步，将力学和电磁学融合在了一起，对学生提出了形成更加庞大的物理观念、建构更加深刻的逻辑体系的要求，学生在这一学习过程中，不断厘清自由电子、电流、安培力、洛伦兹力等物理概念的本质以及相互间的关系，完成物理核心素养的培养.

教师教学中还需要注意结合学生实际的认知水平和学习能力进行调整，在不失认知科学性的前提下，可以结合问题解决模式、项目学习模式、单元整体教学设计等教学手段，引导学生完成自由电子及其受力的相关问题的梳理，尤其是在复习课阶段更应如此，以此促使学生物理概念规律体系的建构与形成.