巧用GeoGebra构建安培力与洛伦兹力的模型*

邓思佳

(闽南师范大学物理与信息工程学院 福建 漳州 363005)

沈 璐

(广东汕头华侨中学 广东 汕头 515000)

付丽萍

(闽南师范大学物理与信息工程学院 福建 漳州 363005)

GeoGebra是一款操作简单、功能强大、免费开源的教学软件.近年来，GeoGebra软件在物理教学中起到了积极的作用[1～3].磁场主题是电磁学的核心内容之一，通电导线和运动电荷在磁场中受力问题一直以来都是高中物理教学中的重点和难点，磁场“看不见、摸不着”的特点使学生缺少直观的感性材料，教学中利用GeoGebra软件通过多种方法构建可视化的物理模型，搭建思维“支架”，帮助学生理解与掌握安培力、洛仑兹力的方向和大小.

1 通电导线在磁场中的受力

安培力的方向和大小是人教版教材选择性必修第二册第一章第1节“磁场对通电导线的作用力”的重点内容.本节课教学的要求是：通过实验，认识安培力.能判断安培力的方向，会计算安培力的大小[4].通过初中的学习，学生已经知道通电导线在磁场中会受到安培力的作用，对安培力的大小和方向有了初步的认识.但通电导线在磁场中所受的安培力方向与电流方向、磁感应强度方向的空间位置关系比较抽象，学生存在着思维障碍.

利用GeoGebra软件构建可视化的物理模型，让学生能清晰地“看见”三者的空间位置关系，帮助学生理解与掌握.

1.1 安培力方向

通过GeoGebra软件构建通电导线在磁场中所受的安培力方向与电流方向、磁感应强度方向三者空间位置关系的物理模型，并利用GeoGebra软件的AR展示功能，引导学生利用左手判断通电导线在磁场中所受的安培力方向.

(1)构建匀强磁场中通电导线模型

第一步：打开3D绘图区、指令栏，勾选平面、网格坐标选项.

第二步：在指令中输入序列“sequence(sequenc e(vector((i,j,8),(i,j,0)),i,-4,4,4),j,-6,6,6)”，便可得到如图1所示的一系列磁感应线，从而构建一个方向为z轴负方向的3D匀强磁场分布模型.

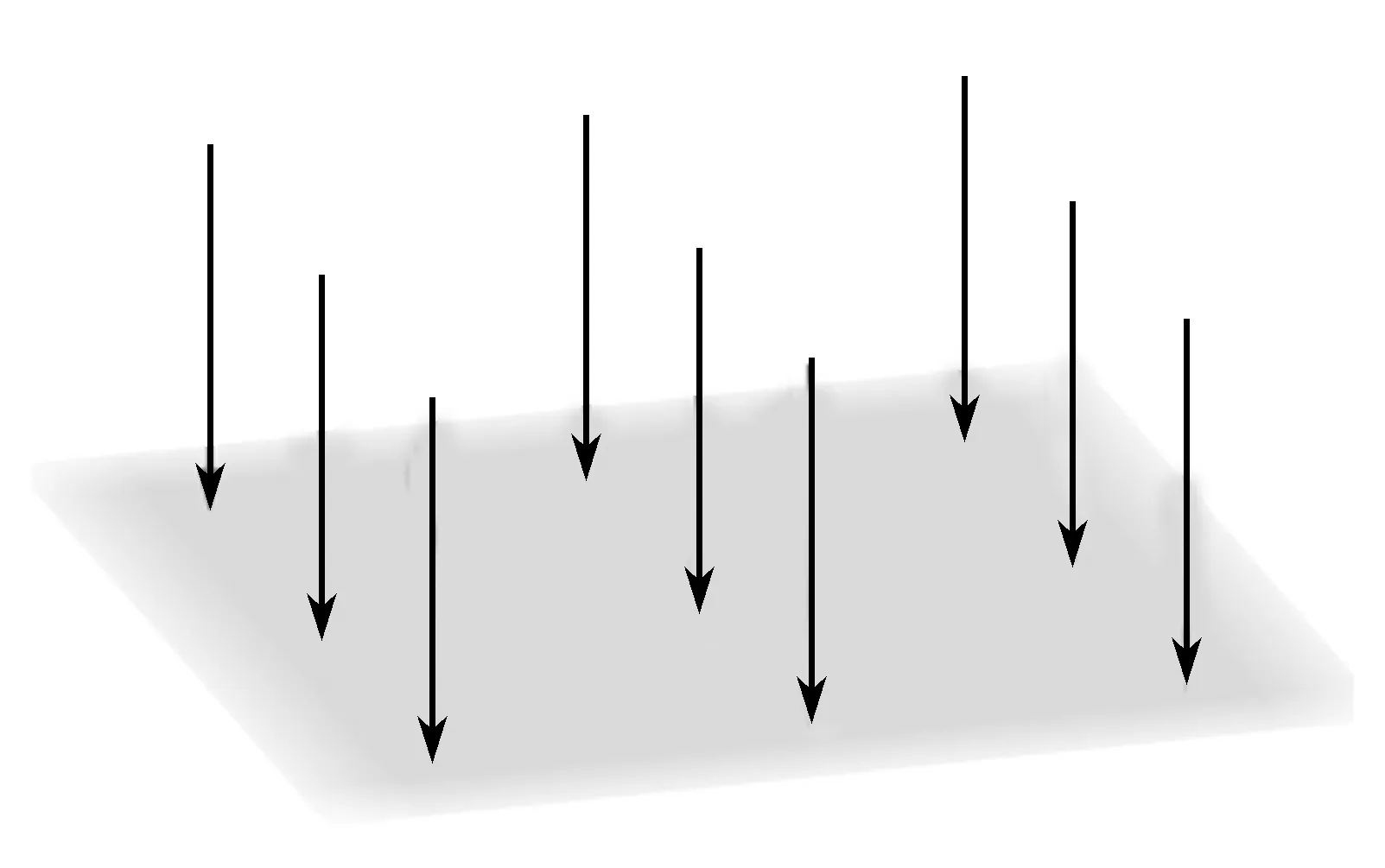
图1 匀强磁场模型

第三步：创建坐标为(5，0，4)和(-5，0，4)的两点，使用线段工具连接这两点，使用向量工具标出此线段的电流方向，可以构建出匀强磁场中通电导线模型如图2所示.

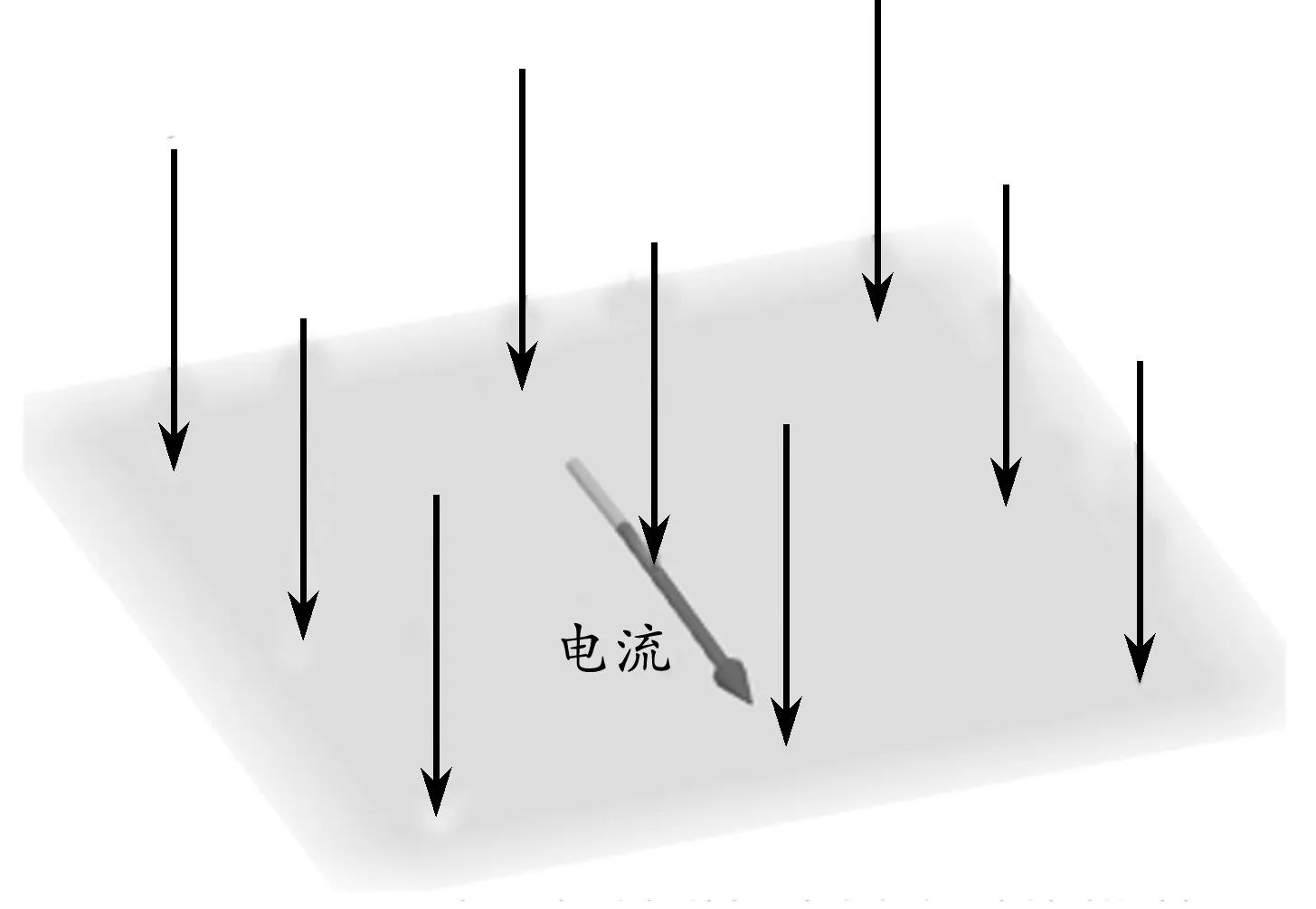
图2 匀强磁场中通电导线模型

(2)构建通电导线在磁场中受力的3D模型

第一步：我们可以通过左手定则判定出通电导线在磁场中所受的安培力方向，并使用向量工具构建出该通电导线所受的安培力方向.

第二步：使用平面工具创建一个法向量与磁感应强度方向垂直且通过安培力向量的平面，立体化地展示了通电导线在磁场中所受的安培力方向与电流方向、磁感应强度方向之间的空间位置关系如图3所示.

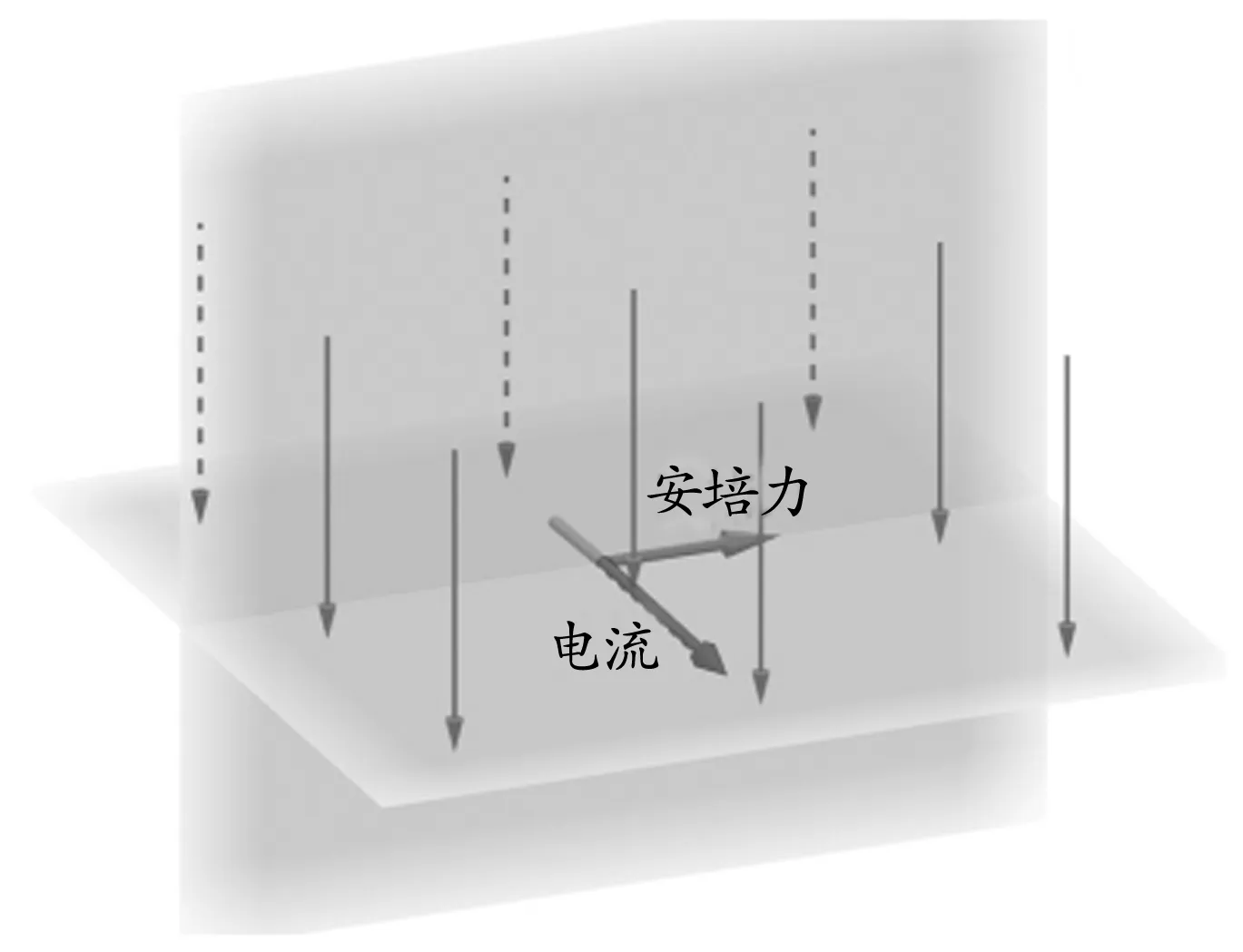
图3 通电导线在磁场中受力的3D模型

第三步：如图4所示,建立安培力、电流和磁感应强度三者方向的空间关系.

图4 安培力方向、电流方向、磁感应强度方向的空间关系

使用平面工具创建一个法向量与磁感应强度方向垂直且通过电流的平面，隐藏所有的磁感应线向量，并创建一个方向为z轴为负方向、以电流向量的起点为起始点的磁感应强度向量.清晰地展示了通电导线在磁场中所受的安培力方向与电流方向、磁感应强度方向之间的3D空间位置关系.

(3)判断通电导线在磁场中所受的安培力方向

GeoGebra软件具有AR展示功能，使用平板将3D模型投影到真实的情景中，让学生切身感受并验证通电导线在磁场中所受的安培力情况如图5所示.

图5 学生摸拟体验

1.2 安培力大小

利用GeoGebra软件的2D绘图功能，可以绘制通电导线在磁场中所受的安培力大小的函数关系图像，能动态化地呈现出通电导线与磁感应强度方向成不同的角度时，通电导线所受的安培力大小变化情况的函数分布图.

(1)通电导线的电流方向垂直于磁感应强度方向

第一步：分别创建名称为B和L的滑动条，滑动条的取值范围分别设置为0～10 T和0～0.5 m，如图6所示.

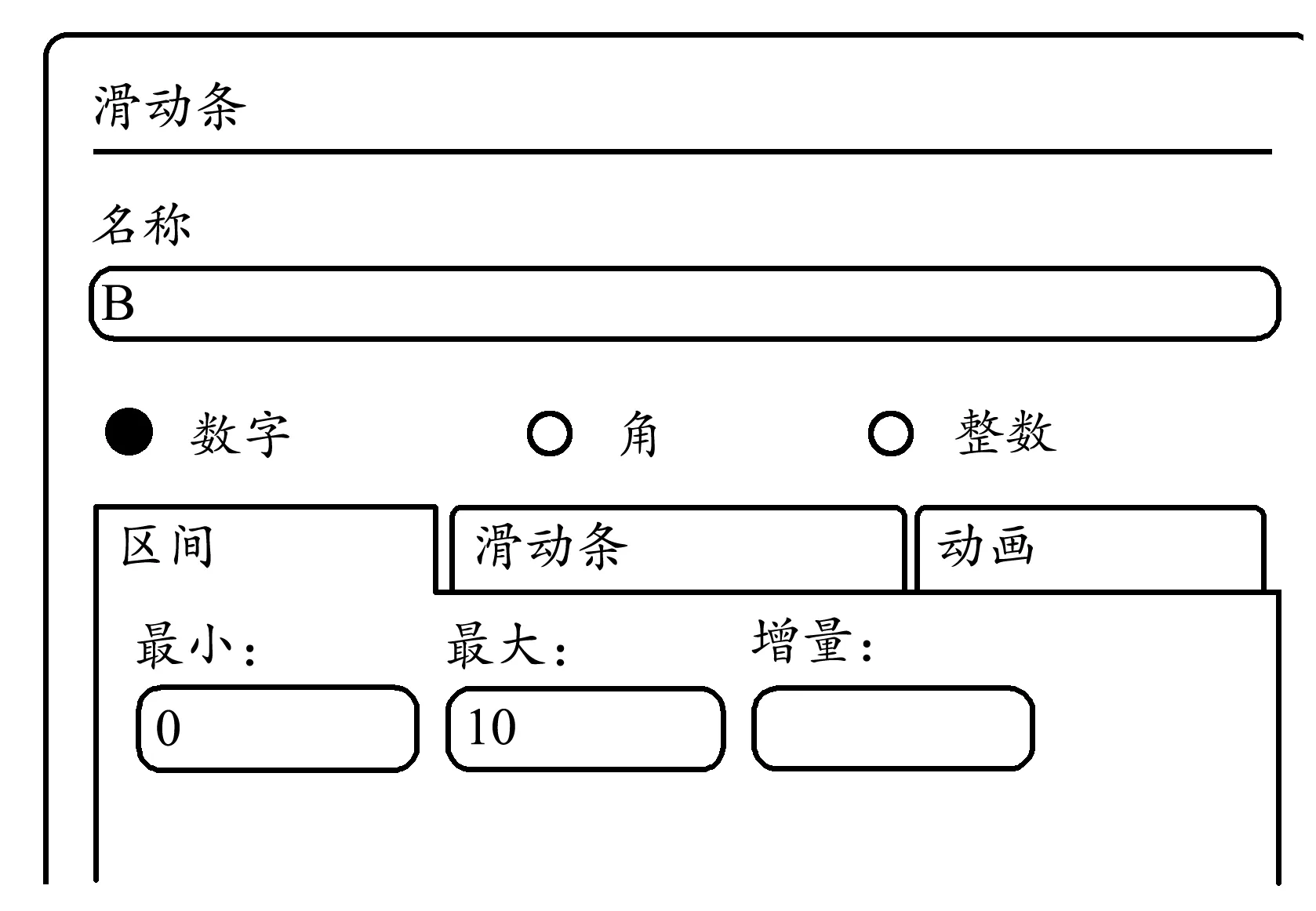
图6 滑动条界面

第二步：在指令栏中输入函数f(I)=BIL,在绘图区上显示出该函数的分布情况(y轴表示通电导线所受的安培力大小，x轴表示通电导线中电流的大小).便可以通过GeoGebra软件演示通电导线中的电流方向与磁感应强度方向垂直时，B和I的变化情况如图7所示.

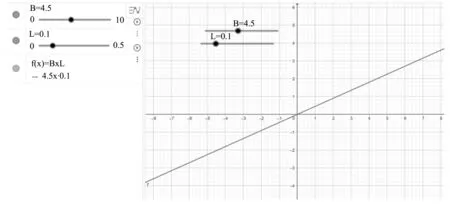
图7 导线的电流方向垂直于磁感应强度方向的函数分布图

第三步：通过改变滑动条B和L的大小，可以得到斜率不相同的函数图像如图7所示.

(2)通电导线的电流方向与磁感应强度方向成θ角

第一步：创建一个名称为I的滑动条，滑动条的取值范围设置为0～10 A.在指令栏中输入函数f(θ)=BILsinθ,在绘图区上显示出该函数的分布情况(y轴表示通电导线所受安培力的大小，x轴表示通电导线中的电流方向与磁感应强度方向所成的角度)如图8所示.

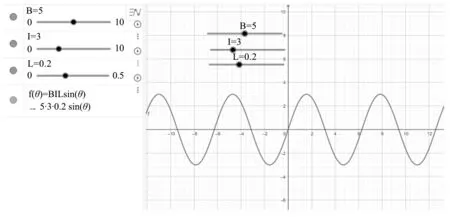
图8 导线的电流方向与磁感应强度方向成θ角的函数分布图

第二步：观察匀强磁场中通电导线的电流方向与磁感应强度方向成θ的角度时，通电导线所受的安培力大小的函数图像.

第三步：通过调节滑动条从而改变B，I，L的大小，我们可以观察到通电导线在磁场中所受的安培力大小随电流、磁感应强度、导线长度、导线与磁感应强度方向的夹角变化而发生改变的动态函数图像如图8所示.

2 运动电荷在磁场中的受力

洛伦兹力的方向和大小是人教版教材选择性必修2第1章第2节“磁场对运动电荷的作用”的重点内容.本节课教学的要求是：通过实验，认识洛伦兹力.能判断洛伦兹力的方向，会计算洛伦兹力的大小[4].运动电荷在磁场中所受的洛伦兹力方向与电荷的运动方向、磁感应强度方向三者的空间关系比安培力的方向更复杂、更抽象，不容易直接观察，学生理解起来比较困难.可利用GeoGebra软件的3D绘图功能绘制出运动电荷在匀强磁场中受力的物理模型辅助教学，实现教学要求.

2.1 洛伦兹力的方向

借助GeoGebra软件的3D视图，构建运动电荷在磁场中所受的洛伦兹力方向与运动方向、磁感应强度方向之间的空间关系模型.

(1)构建运动的正电荷在磁场中的3D模型

第一步：使用圆柱工具构建微观下的通电导线模型，将圆柱体模型底面的半径设置为4，使用向量工具构建出此圆柱通过电流的方向.

第二步：使用序列工具，在指令栏中输入序列“Sequence(Sequence(Sequence((i,j,k),i,-1,1,2),j,-4,4,4),k,3,5,2)”,便可创建一系列运动的正电荷模型.

第三步：在指令栏中输入序列“Sequence(Sequence(Sequence(Vector((i,j,k),(i,j-1.5,k)),i,-1,1,2),j,-4,4,4),k,3,5,2)”,便可标出这一系列运动的正电荷的运动方向如图9所示.

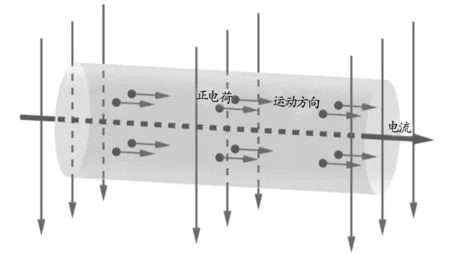
图9 匀强磁场中正电荷的运动模型

(2)构建运动的正电荷在磁场中的受力模型

根据左手定则，我们能够判断出以上一系列运动的正电荷在磁场中所受的洛伦兹力方向，并使用序列工具绘制出运动的正电荷所受的洛伦兹力方向如图9所示.

第一步：在指令栏中输入序列“Sequence(Sequence(Sequence(Vector((i,j,k),(i+1.5,j,k)),i,-1,1,2),j,-4,4,4),k,3,5,2)”，标出运动的正电荷在磁场中所受的洛伦兹力的方向如图10所示.

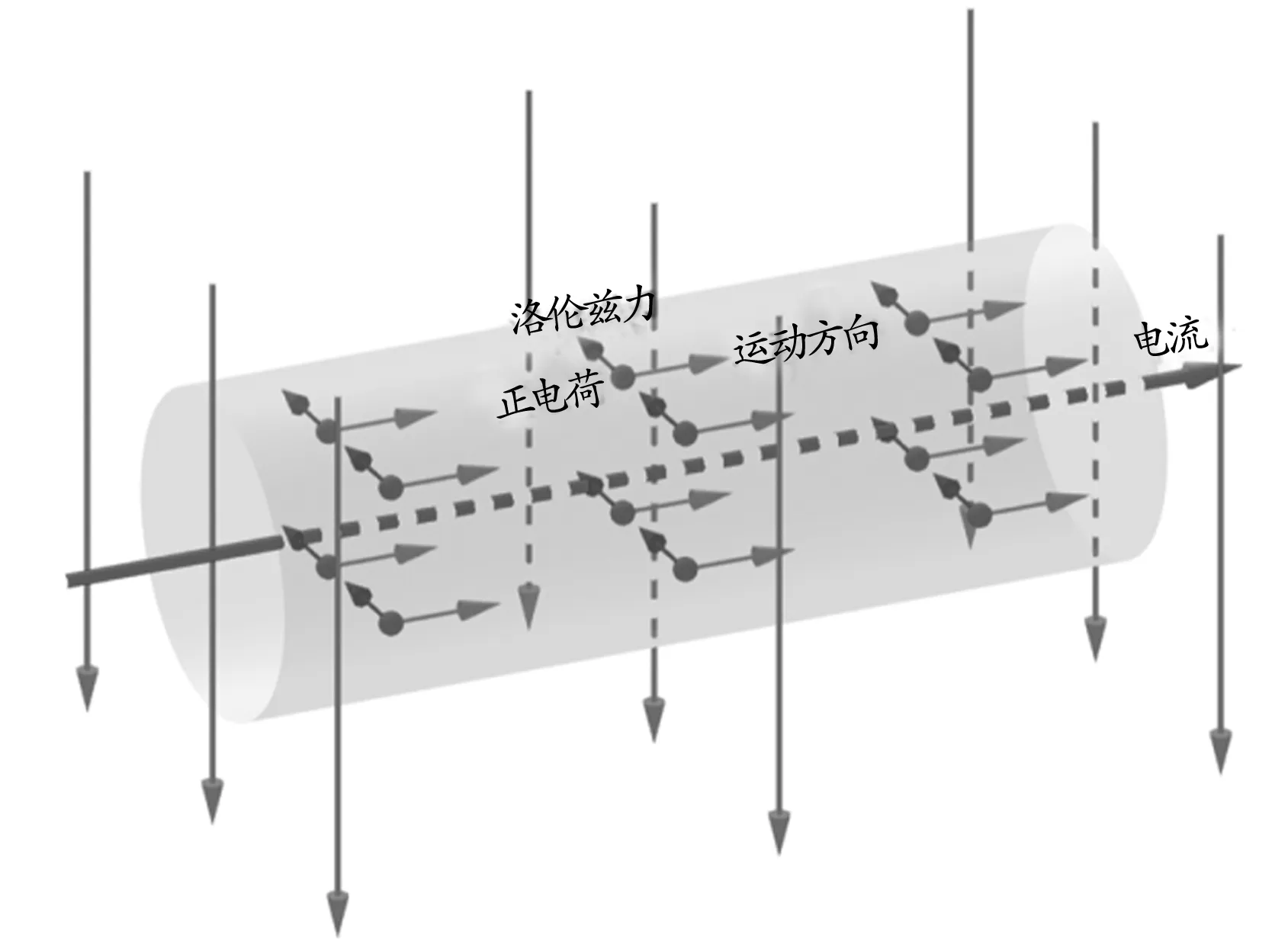
图10 匀强磁场中运动的正电荷的受力模型

第二步：构建在匀强磁场中通电导线内单个运动的正电荷受力情况的3D模型.创建位置为坐标轴原点的点，将其命名为正电荷.以此正电荷为起点使用向量工具分别创建沿x轴正方向、y轴正方向、z的负方向的向量，并将其分别命名为洛伦兹力、运动方向、磁感应强度方向.

第三步：使用平面工具，分别绘制yOz、xOz、xOy这3个平面的平面模型，从而构建单个运动的正电荷在磁场中所受的洛伦兹力方向与电荷运动方向、磁感应强度方向之间的3D空间分布情况如图11所示.

图11 洛伦兹力方向、电荷的运动方向、磁感应强度方向的空间关系

(3)匀强磁场中正电荷的运动

在匀强磁场中，正电荷做圆周运动.正电荷所受的洛伦兹力提供其做圆周运动的向心力.通过GeoGebra软件的3D绘图功能，能够动态、清晰地展现通电导线中单个运动的正电荷在匀强磁场中的运动情况.

第一步：在2D绘图区创建一个滑动条，将其命名为r.在洛伦兹力向量的方向上创建一点为圆的圆心.

第二步：以该点为圆心使用圆工具，以r为半径，通过调节滑动条r使圆与运动的方向相切.

第三步：使用“对象上的点”工具，分别在圆的轨迹上选择正电荷的出发点、经过点、射出点.使用圆弧工具连接这3点.隐藏原来圆的轨迹，可以得到通电导线中的正电荷的运动轨迹如图12所示.

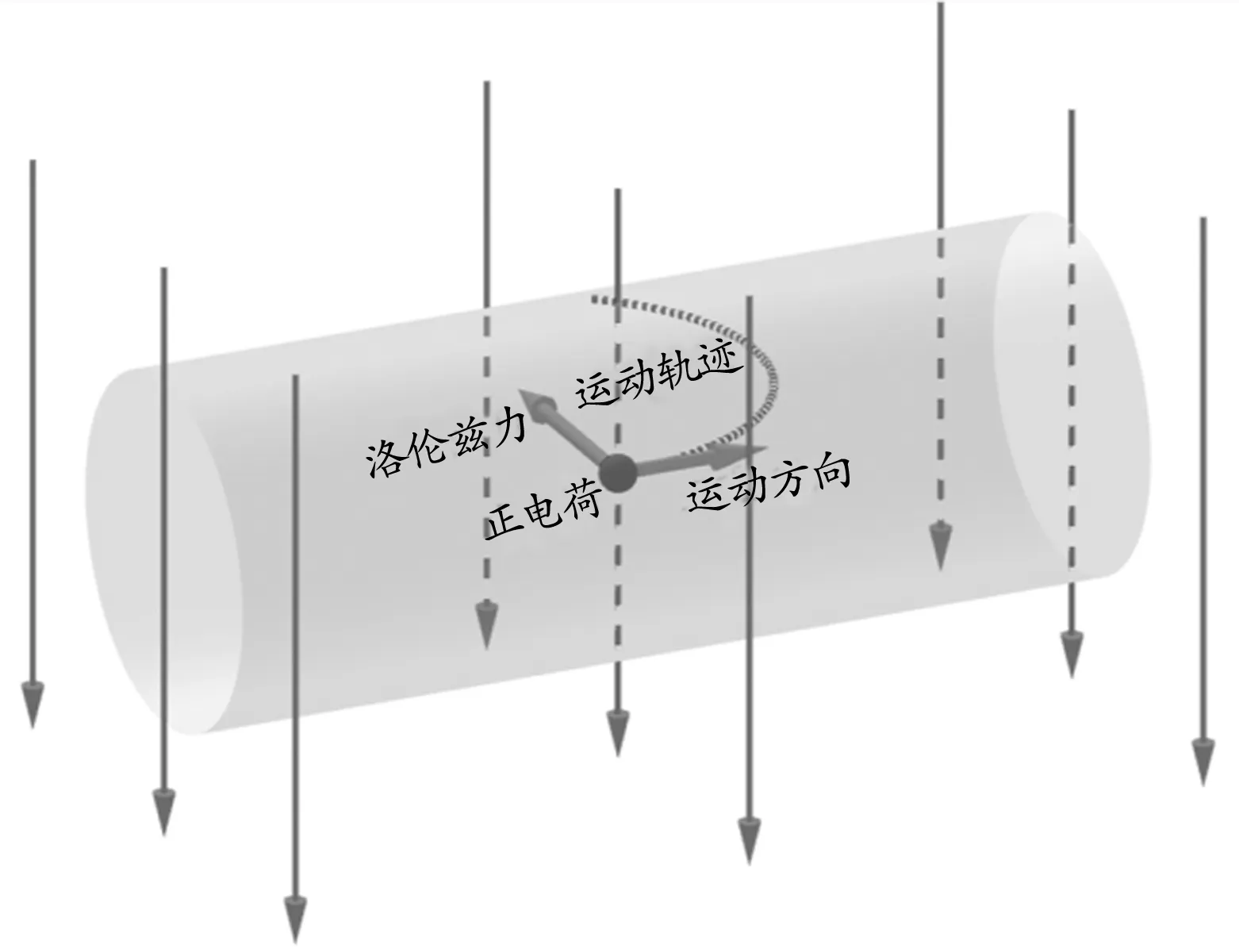
图12 单个正电荷在匀强磁场中的运动轨迹

第四步：在洛伦兹力方向上创建一个点为圆心，以r(滑动条名称)为半径、z轴为法向量构建一个圆，调节滑动条使得圆与正电荷的运动方向相切.便可得到洛伦兹力方向、正电荷的运动方向、磁感应强度方向、正电荷的运动轨迹之间的空间关系如图13所示.

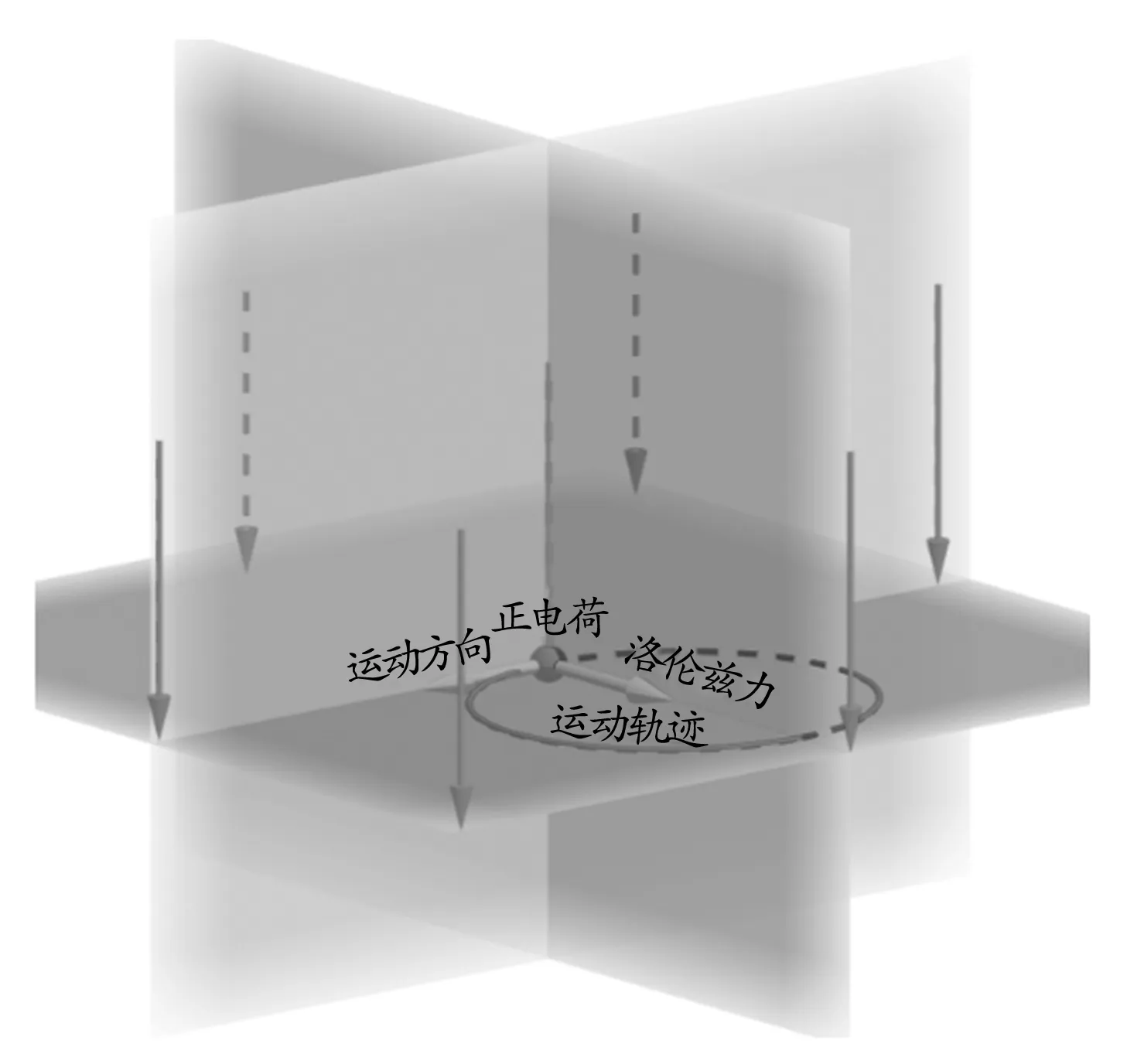
图13 洛伦兹力方向、正电荷运动方向、磁感应强度方向、正电荷运动轨迹的空间关系

(4)判定运动的正电荷在磁场中的受力方向

GeoGebra软件具有AR展示功能，使用平板将3D模型投影到真实的情景中，让学生切身感受并验证运动的正电荷在磁场中所受的洛伦兹力的情况如图14所示.

图14 学生摸拟体验

2.2 洛伦兹力的大小

使用GeoGebra软件的2D绘图功能可以构建运动电荷在磁场中所受洛伦兹力大小的函数关系，可以直接将运动电荷在磁场中所受的洛伦兹力大小与运动的速度、磁感应强度、运动电荷的电荷量之间的数学关系用函数图像表现出来.

(1)电荷运动的方向垂直于磁感应强度方向

第一步：分别创建名称为B和q的滑动条，滑动条的取值范围分别设置为0～107T、0～10-7C.

第二步：在指令栏中输入函数f(v)=qvB(y轴表示洛伦兹力的大小，x轴表示运动的正电荷的速度大小).

第三步：通过调节滑动条改变B和q的数值大小，我们可以清晰地观察到电荷运动的方向与磁感应强度方向垂直时B和v的变化情况，可以得到斜率不相同的函数图像如图15所示.

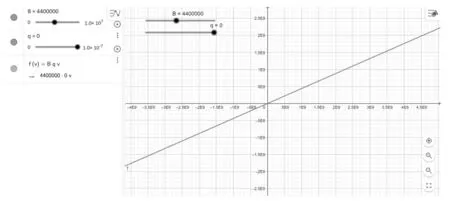
图15 电荷的运动的方向垂直于磁感应强度方向的函数分布图

(2)电荷的运动的方向与磁感应强度方向成角度

第一步：创建一个名称为v的滑动条，取值范围设定为0～107m/s.

第二步：在指令栏中输入函数f(θ)=qvBsinθ,在绘图区上显示出该函数的分布情况(y轴代表运动电荷在磁场中所受的洛伦兹力大小，x轴表示电荷运动的方向与磁感应强度方向所成的角度).

第三步：通过GeoGebra软件演示在匀强磁场中电荷的运动方向与磁感应强度的方向成θ的角度时，运动电荷所受洛伦兹力大小的变化情况.我们可以观察到匀强磁场中的运动电荷与所受的洛伦兹力大小随电荷运动的速度大小、磁感应强度、运动电荷的电荷量、电荷的运动方向和磁感应强度方向所成的角度的变化而发生改变的动态函数图像如图16所示.

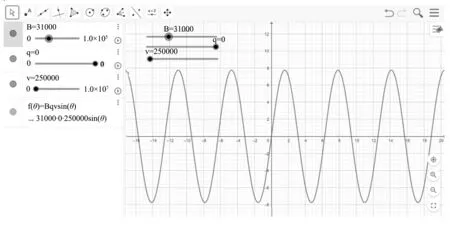
图16 电荷的运动的方向与磁感应强度方向成θ角的函数分布图

3 结束语

GeoGebra软件操作简单易学、易用，构建的物理模型生动形象、直观.巧用GeoGebra软件绘图功能构建通电导线与运动电荷在磁场中受力的模型，为学生提供感性认识，使抽象的知识形象化，微观的现象可视化.巧用AR展示功能将3D模型投影到真实的情景中，让学生模拟体验，产生身临其境之感，促进学生的理解.在教学中积极开发信息化技术的教学资源，探索信息技术与物理教学的深度融合，是当今信息时代对物理教师的诉求.