基于艏艉全参数建模及自航计算的线型优化

陆琛亮， 杨 博， 张淇鑫

(上海船舶研究设计院， 上海 201203)

0 引 言

船舶线型设计与船舶的各项重要指标(油耗、航速、载重量和舱容等)有着密不可分的关系。常规的船舶线型优化设计通常采用软件手工修改与自动变换相结合的方式进行，通过计算流体力学(Computational Fluid Dynamics，CFD)计算优化减小船体的兴波阻力和黏压阻力，而由于设计周期和计算时间等因素的限制，带螺旋桨的自航计算一般会省略，取而代之的是通过比较艉部伴流优选多个阻力较小的方案，以期在优选出小阻力线型的同时，提升螺旋桨的工作效率。

本文以一艘低速肥大型散货船为例进行分析，此类船型的快速性优化往往不能局限于对兴波阻力和黏压阻力进行优化，不同的艉部设计往往会有不同的螺旋桨效率表现，有时甚至有较大的差异。因此，通过自航计算优化降低螺旋桨的收到功率非常必要。本文详细介绍艏部和艉部全参数建模变换与自航计算相结合的优化方法，最终优化得到螺旋桨收到功率最小的船体线型。

1 目标船基本情况

本文优化的目标船是一艘20万吨级散货船，总长约310 m，弗劳德数约为0.139，兴波阻力占比较小，此时优化兴波阻力对总阻力优化的收效较小，黏性阻力占比较大，且艉部设计不同会导致螺旋桨效率存在较大差异，对于此类船型的优化而言，应对船体总阻力和螺旋桨效率进行综合优化。

2 船体建模方法

首先需对目标船的艏部和艉部进行参数化建模，建模工具为德国FRIENDSHIP SYSTEMS公司开发的软件CAESES。该船采用的建模方法同样适用于集装箱船和油船等单艉鳍船型。

参数化建模是指通过一系列参数建立船体曲面，这种建模方法的优势是能通过个别参数的变化迅速变化出具有不同特征的线型，并能直接用于CFD计算，大大增加优化方案的数量，提高优化的效率和效果。

船体建模分为艏部、艉部和舯部(平行中体)等3部分，下面具体介绍参数化建模方法。

2.1 艏部建模

2.1.1 艏部主要参数的名称及数值

艏部主要参数的名称和数值：xFp为垂线间长；beam为船宽；draft为吃水；height为型深；bowOverang为球艏长度；xPeak为船体最前端

x

值，等于xFp+bowOverang；xMainFrame为艏部最大横剖面

x

位置；bilgeHeight为舭部高度；bilgeWidth为舭部宽度；relXFwdBase为平底线前端位置系数；xFwdBase为平底线前端位置，等于xMainFrame+relXFwdBase×(xFp-xMainFrame)。

2.1.2 艏部最大横剖面的定义

根据上面定义的舭部高度bilgeHeight、舭部宽度bilgeWidth和舭龙骨的丰满度系数Coeffbilge生成舭部曲线bilge curve，目标船的Coeffbilge取0.805。

2.1.3 艏部各特征曲线的定义

艏部各特征曲线的分类及命名：deck为甲板线；dwl为设计水线；flareAtDeck为甲板处的外飘角分布曲线；flareAtDwl为水线处的外飘角分布曲线；fob为平底线；fos为平边线；sac为横剖面面积曲线；stem为艏柱。各曲线形式见图1。

图1 艏部初始特征曲线

2.1.4 艏部各曲面的定义

船体曲面构成的原理为：首先通过上述各特征曲线生成CAESES软件中称为curve engine曲线的特征函数，然后通过此curve engine沿船长方向生成一条条横剖线，最后通过CAESES特有的曲面形式MetaSurface连接成光顺曲面。这样所得船体曲面必然满足上述特征曲线的要求。

但是，由于船舶曲面的复杂性，不可能从最大横剖面至球艏只用1个特征函数(即curve engine)生成横剖线，因此按特征曲线的分布，将船体表面分成10个曲面，10个曲面光顺过渡连接之后才能形成一个完整的艏部曲面。10个曲面的分类及命名：mid2FosEmerge为从最大横剖面至设计水线平边线相交处的曲面；fosEmerge2Fwd为从设计水线平边线相交处至平边线最前端的曲面；fosFwd2Base为从平边线最前端至平底线最前端的曲面；base2Fp为从平底线最前端至艏垂线处，设计水线以上的曲面；fillet为从平底线最前端至艏垂线处，设计水线以下的曲面；topFillet为base2Fp与fillet之间的填充曲面；stem为艏柱附近的曲面；tube为base2Fp与stem之间的填充曲面；bulb1为从艏垂线至其前端1.4 m处的曲面；bulb2为从艏垂线往前1.4 m至球艏最前端的曲面。各曲面形式见图2。

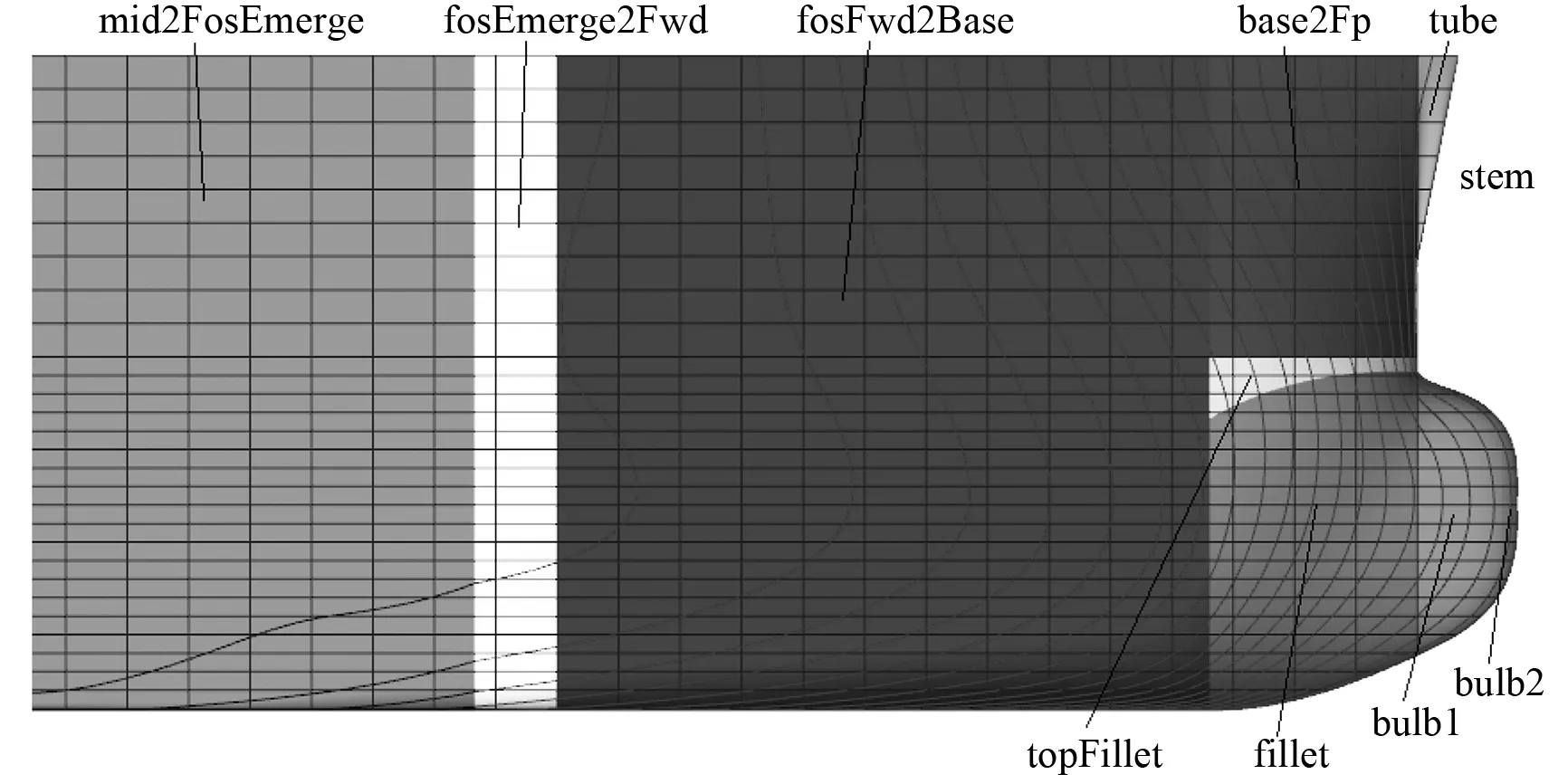
图2 目标船各曲面形式

2.2 艉部建模

艉部建模的原理为：首先单独创建一个不含艉鳍的裸船体，然后建一个艉鳍与裸船体光顺过渡，最后去掉裸船体与艉鳍相交处裸船体上多余的部分，形成一个完整的艉部模型。

2.2.1 裸船体艉部主要参数的名称及数值

裸船体艉部主要参数的名称及数值：xAftBase为平底线趋势线后端；xBilgeAft为平底线趋势线前端，取0.5倍的xMainFrame；xMainFrame为艉部最大横剖面

x

位置；xTransom为艉封板尾端

x

位置；zTransom为艉封板尾端高度。

2.2.2 裸船体艉部最大横剖面的定义

最大横剖面定义与艏部一致，而艉部最大横剖面所在

x

的位置不同。

2.2.3 裸船体艉部各特征曲线的定义

裸船体艉部各特征曲线的分类及命名：keel为船底基线；fos为平边线，分前后2段；fob为平底线，分前后2段；deck为甲板边线，分前后2段；fos_tangent为平边线进入角，最大为90，分前后2段；bilge_fullness为横剖线丰满度，分前后2段。裸船体艉部各特征曲线见图3和图4。

图3 裸船体艉部各特征曲线侧视图

图4 裸船体艉部各特征曲线俯视图

2.2.4 艉鳍各特征曲线的定义

就合作学习而言，主要是通过组织开展合作的方式，学习相关知识。新时期，开展语文教学，需要通过分工合作的形式，共同完成学习任务。要运用这种新型的合作学习的教育方式，需要教师对此共同作出努力。在进行合作学习的过程中，要求教师端正自身的态度，采用科学的学习方法，充分应用传统教学的优点，然后将其与合作学习相结合。不仅要关注学生的学习成绩，还要关注其成长过程中出现的一些问题，促使学生在参与合作学习的过程中，学到更多有用的知识。如在大课间的时候，可以组织学生玩“成语接龙”“你比我猜”等游戏，既丰富了学生的课外活动，又能从中学到很多文化知识，增强了学生合作能力，让其更具有团队合作意识。

艉鳍各特征曲线的分类及命名：boundary为艉鳍与船体的相交线；intermediate为艉鳍与艉鳍出口端边线之间的过渡线；boss为艉鳍出口端边线。艉鳍各特征曲线见图5。

图5 艉鳍各特征曲线

2.2.5 艉部各曲面的定义

艉部建模得到的2个面见图6，其中：hull为裸船体；skeg为艉鳍。

图6 目标船各曲面的形式

裸船体与艉鳍相交内的裸船体表面需要删除，从而组成一个完整的带艉鳍的船体，局部删除之后的裸船体根据相对于艉鳍的位置分成4个面，其中：behindSkeg为艉鳍后的面；besideSkegAft为艉鳍边的面(后)；besideSkegFore为艉鳍边的面(前)；beforeSkeg为艉鳍前的面。最终形成的船体见图7。

图7 最终形成的船体

2.3 平行中体建模

平行中体的建模较为简单，将艏部与艉部最大横剖面之间的间隙填上即可。

3 全参数优化

3.1 参数变量优化

用于生成船体的参数变量非常多，其中影响船体快速性能的参数变量同样非常多，因此为提高线型优化的效果和效率，需根据设计者的经验选取有限的优化变量。

3.1.1 整体参数变量

船体整体变化采用Lakenby变换的方法实现，该方法用于改变横剖面面积曲线，从而优化浮心纵向位置、排水体积、水线进水角和出水角等重要的线型实现参数。

3.1.2 艏部参数变量

3.1.3 艉部参数变量

艉部优化对于目标船来说至关重要，因此选取较多的参数变量，涉及艉鳍的丰满度、横剖面UV度、纵剖线斜度和艉封板尺度等重要船体艉部线型特征。在这些参数中：aft_bilge_fullness_mid为横剖面最大丰满度；aft_bilge_fullness_part1为后横剖面最大丰满度曲线的丰满度；aft_cpc2_fullness为船底基线的丰满度；aft_dk_part1_fullness为后甲板边线的丰满度；aft_dk_part1_tangent为后甲板边线的艉端进入角；aft_fos_tangent_part1为后平边线的进入角；aft_skeg_width为艉鳍上边界宽度；aft_width_Factor为艉鳍中间过渡线宽度系数；aft_boundary_fullness为艉鳍上边界丰满度；aft_xdeckmax为甲板最大船宽处

x

的最小值；aft_xTransom为艉封板末端的

x

值；aft_yTransom为艉封板末端的半宽值；aft_zTransom为艉封板末端的最小高度。

3.2 船体限制条件

为使优化得到的线型满足实际的总体及轮机等设计要求，需给定一些限制条件，本文所述目标船主要有以下2个限制条件：

1) 排水体积和浮心位置，通过艏艉模型参数和全局横剖面面积曲线的Lakenby变换调整；

2) 2个限制点，分别位于主机和货舱位置，分别在2站和19站位置，通过限制点到船体曲面的最小距离进行判断，若该距离小于零，则说明限制点在船体曲面之外，即不满足设计要求。

3.3 优化方法与目标

目标船以设计吃水、15 kn航速为优化点，以降低该状态下的螺旋桨收到功率

P

为优化目标。优化分2轮进行，其中：第一轮为阻力优化，减小阻力不仅有助于成功实现线型优化，而且能加快阻力计算速度，先进行阻力计算可先对船体进行整体上的优化；第二轮为收到功率优化，即自航计算，2种计算均基于模型尺度进行，模拟水池阻力和自航试验得到模型尺度下的螺旋桨收到功率

P

，最终优化目标是使螺旋桨收到功率

P

最小。若时间允许，还可进行第二次迭代优化，进一步优化阻力和功率。

用于计算的软件是FLOWTECH公司的CFD软件SHIPFLOW，分别包括阻力计算模块和自航计算模块。

3.3.1 阻力计算优化

阻力计算采用势流与黏流相结合的方法，分别采用SHIPFLOW中的XPAN兴波阻力计算模块和XCHAP黏性阻力计算模块进行计算，目标船的弗劳德数为0.139，模型尺度雷诺数为5.48×10。

由于阻力计算速度较快，黏性计算网格采用global方法生成，网格数相对于自航计算更多，约180万个。

3.3.2 自航计算优化

自航计算更为耗时，需进行一定的简化，黏性计算网格采用zonal方法生成，即只对船体后半部分建立黏流计算网格，并进行黏流计算，这样可大大减少网格数量，缩短黏流计算时间，采用该方法的计算网格数约为50万个。

SHIPFLOW中的自航计算有3种方法。

1) 固定转速: 给定转速计算推力扭矩。

2) 自动：计算阻力，敞水，推力扭曲，寻找推力与阻力的平衡点。

3) 用户自定义：给定强制力系数，计算速度快。

考虑到仅优化1个速度点的功率，选用第三种方法进行自航计算，设置文件中的Prop命令给定桨盘面的

x

位置、桨轴高度、桨直径和桨榖直径，螺旋桨敞水计算采用升力线法，螺旋桨几何文件需输入桨叶数、盘面比、0.2～1.0半径处的螺距比、弦长、厚度和拱度等参数。

3.4 优化算法和优化结果

优化变量的数量较多，艏部变量有5个，艉部变量有13个，变量的组合通过CAESES中自带的Sobol优化算法生成，针对第3.3节所述的2轮优化，选取不同优化变量和变换范围，以减少优化方案的计算数量，在进行阻力优化时尽量减少艉部变量的变换范围，在进行自航优化时减少艏部的变量，把重点放在艉部变量优化上。采用Sobol优化算法生成的变量组合示例见图8。

图8 采用Sobol优化算法生成的变量组合示例

进行2轮线型优化之后得到2种线型方案，分别是基于阻力计算优化的线型和基于自航计算优化的线型。

采用SHIPFLOW得到的2种方案的计算结果对比见表1，其中：SHIPFLOW中的兴波阻力系数有

C

和

C

2种，

C

由船体表面的压力得到，

C

通过水面兴波得到；

W

为桨盘面处的名义伴流；

C

为摩擦阻力系数；

C

为黏压阻力系数；

C

为黏性阻力系数，即

C

与

C

之和；

K

为形状因子；

S

为无因次湿表面积；

P

为螺旋桨收到功率。2种线型方案伴流对比见图9，线型对比见图10。

表1 2种方案计算结果对比

图9 2种线型方案伴流对比

图10 2种线型方案的线型对比

由计算结果和线型对比分析可知：基于阻力计算优化的线型的黏压阻力系数比基于自航计算优化的线型的黏压阻力系数小2.86%，兴波阻力系数相当，而基于自航计算优化的线型的艉部外侧更为丰满，伴流稍大，且分布更加均匀，最终的收到功率明显更小，比基于阻力计算优化的线型小4.2%。由此可知，虽然基于自航计算优化的线型在阻力上并不占优，但由于该线型艉部产生的伴流更有利于螺旋桨推进，使得螺旋桨推进效率较高，最终螺旋桨的收到功率更小，快速性能更优。

4 结 语

船体艏部和艉部全参数建模和变换是进行线型优化的有效方法。阻力计算相对来说速度较快，有利于开展大量方案的优化计算。对经过阻力计算优化的方案进行自航计算优化，目标船的螺旋桨收到功率可进一步减小。同时，参数化变换可设定多种限制条件，从而得到满足实际使用要求的快速性能更优的模型。