小学数学几何概念建模之实践探究
张宏


[摘 要]对学生来说,几何概念一般是比较抽象的,学生直接认识起来比较费力,因此对于几何概念的建模,一直是许多教师想着力解决的问题。教师总结出几何概念建模的几个注意点:一是要重视从具体到抽象的过程;二是要重视对几何概念本质的探究;三是要重视变式的运用。
[关键词]几何概念;建模;三角形的高
[中图分类号] G623.5[文献标識码] A[文章编号] 1007-9068(2021)29-0076-02
在小学数学教学中,有关几何概念的教学是一个比较重要的内容。学生在学习时,对于几何概念往往把握不准。如何对几何概念进行建模,笔者做了很多尝试。就拿“认识三角形”这堂课来说,这是一节典型的几何概念教学课,课程要求学生认识三角形的基本特征、知道什么样的图形是三角形,并且认识三角形的高。对于“三角形的高”这一几何概念,不同的施教者采用的教学设计也不同,每一个设计在今后进行几何概念建模时都有一定的指导意义。下面笔者就以“认识三角形的高”教学为例,谈一谈在进行几何概念建模时应该注意的几个方面。
一、重视从具体到抽象的过程
概念一般都是比较抽象的,几何概念也不例外,学生直接认识起来比较费力,因此对几何概念的教学,教师需要通过具体事物引导学生去抽象、概括、认识。
例如,在“认识三角形”这一节课中对于“三角形的高”的认识,教学设计如下。
师:一些房屋的顶部是包含了三角形的“人字梁”结构,大家请看,从图中(图1)你能量出“人字梁”的高度吗?你量的是哪条线?
(单位:米)
生:量最中间的那条。
师:如果我只留下外面的三角形(图2),你还能量出它的高吗?怎么量的?(教师让学生在黑板上演示量法,演示完后,教师顺势讲解三角形的高的概念,并介绍三角形的高的画法)
对于初学者来说,“三角形的高”这个知识点要想真正理解是比较费力的,教师先是让学生找出能代表“人字梁”高度的那条高,紧接着将“人字梁”抽象为一个三角形,再让学生去找三角形的高,将找具体事物的高转变为找三角形的高。学生在“人字梁”的支撑下,通过脑海中建立的表象很顺利地找出三角形的高。
二、重视对几何概念本质的探究
对于“一个几何概念,为什么这样界定”的问题,学生不但要知其然,而且要知其所以然。对于几何概念“三角形的高”,如果学生只是认识了高和会作高,那还仅仅是停留在知识的表面。大家都知道,三角形的高是顶点到对边的垂直线段,虽然是简简单单的一句话,但是要想真正理解高,就需要知道三角形的高到底影响了三角形的什么特性,教师要让学生透过现象看本质,从而建构 “三角形的高”这一几何概念。
师:这两个三角形有什么不同(图3)?
生1:高度不同,左边的三角形个子矮,右边的三角形个子高。
(教师隐去左边的三角形)
师:你会量三角形的高吗?
(学生独立操作,教师请学生上台演示并总结量法)
师:其实测量三角形的高就跟测量人的身高类似,你能从下图中(图4)找到两者的共同点吗?
生2:都要站得直直的,而且要量最顶端。
教师先通过一高一矮两个三角形,让学生关注到两个三角形的不同点在于它们的高度不一样,这其实就是两个三角形底边上的高不同所引起的。接着教师让学生自己尝试测量三角形的高,由于学生脑海中已经初步有了对高的印象,自然会尝试着测量它的高,这个时候教师再适时纠正、总结方法,最后比较测量身高的方法与测量三角形的高的方法,找出两种测量方法的共同点,学生就能很自然地把握住三角形的高的本质特征:三角形的高其实就是顶点到对边的垂直线段。
三、变式的运用可以内化几何概念的建模
学生如何将学到的几何概念进行再加工,并内化为自己的知识,这需要教师采用多变的手段将几何概念进行深度加工。前面学生已经初步认识了三角形的高,但这是不够的,在认识三角形的高时,需要打破学生的思维定式,让学生体会三角形的高和底的对应关系,并且通过探索知道三角形高的条数,下面的三种设计通过不同的方法恰如其分地做到了这一点。
【设计一】
师:请同学们将下面这三个三角形底边上的高画出来(图5)。
师:大家都能很快地将三角形底边上的高画出来,这三个三角形有怎样的特点?
(学生一脸茫然,教师将三个三角形重叠得到图7后学生恍然大悟)
师:其实这三个三角形是同一个三角形。大家观察一下,发现了什么?
生:这个三角形一共有3条高,它的每一条边都可以作为底,并且每条底都有与它对应的高。
学生往往会形成思维定式:三角形的底只能是最下面的一条边,三角形的高一定是从上至下的。那怎样打破这种思维定式呢?只要通过旋转,让三个三角形合为一体,学生就会豁然开朗:原来刚刚画的高其实是同一个三角形不同边所对应的高啊!学生对三角形的高的认识得到完善。
【设计二】
师:请同学们分别将三个三角形底边上的高画出来(图8)。
学生给出以下答案(图9)。
师:从这些答案中,你们发现了什么?
生:这三个三角形都是一样的,但不同的底对应不同的高。
直接出示图8,底标在了同一个三角形中不同的边上,学生自然体会到三角形的每条边都可以作为底,在画出每条边对应的高后,将三个图形重合,让学生明白一个三角形有3条高。
【设计三】
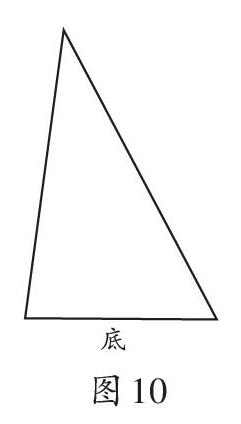
师:请同学们画出以下三角形的高(图10)。
(学生给出如图11所示答案)
(教师将图11在视屏展示台上进行手动旋转,让学生观察)
师:通过观察,你们发现了什么?
生:底和高是对应的,底在动,高也在动。
这一设计,原先只标注了三角形最下面的一条边为底,让学生画高,在学生画完高后,通过旋转图形,让底转到不同的位置,学生体会到底不一定都是在最下面,进而理解三角形的三条边都可以作为底,对底和高的对应关系有了深刻的认识。
三种设计都是通过三角形的高的变式,让学生在变化中体会三角形的底和高的对应关系,并知晓一个三角形有3条高。由上可见,变式的运用对几何概念建模的重要性。
借鉴以上对“认识三角形的高”的不同设计和分析,在今后对于几何概念的建模中,笔者相信大家一定能有所收获。
(责编 黄 露)

