热工水力系统程序RELAP 5的CCFL模型适用性分析

江鹏浩, 李 冬

(上海电力大学 能源与机械工程学院, 上海 200090)

冷却剂丧失事故(Loss of Coolant Accident,LOCA)是限制核电厂功率运行的重要设计基准事故之一。它是指一回路出现破口造成冷却剂丧失,堆芯未得到冷却导致温度升高甚至烧毁的事故[1-2]。在发生LOCA时,一回路冷却剂流量和压力下降,冷却剂可能无法继续按正常的工况进行循环,安注系统提供的冷却水要通过下降段向下注入堆芯,但堆芯内的大量蒸汽通过下降段向上从破口流出,产生了气液相向流动相互作用。倒流的冷却剂流量将会受到蒸汽的影响而减少,发生相向流动限制(Counter-Current Flow Limitation,CCFL)现象[3],从而影响事故的进程。CCFL现象的存在,使得冷却剂流量无法继续增加,削弱了传热效果。

由于CCFL现象的机理复杂,反应堆中不同结构处的气液相间作用特殊,因此需要针对不同结构的特点来研究合理的描述气液相间作用的模型[4],从而为安全设计提供参考,有效控制CCFL现象的发生。CCFL现象容易发生在气液流动方向相反的结构中。由于密度差和重力的影响,所以失水事故后,竖直管道中极易发生CCFL现象且非常明显。另外,在反应堆的各个结构中,竖直管道数量最多,因此研究竖直管道中CCFL现象的形成机理最具有代表性,并且对整个反应堆的安全运行有着重要意义[5]。

文献[6-7]通过实验和理论分析提出,CCFL的作用机理会随着管径的改变而发生转变。文献[8]通过研究发现,管道直径在一定范围内时,Wallis形式的数学关系式较Kutateladze形式的公式更适合拟合CCFL预测模型;在管径超出这一范围继续增大时,考虑到表面张力的影响,Kutateladze形式的数学关系式较Wallis形式的公式更适合拟合CCFL预测模型,但是目前对于管道影响CCFL机理的临界点仍存在较大争议。

目前CCFL现象的研究一般通过实验研究和数值模拟研究两种方式。实验回路的搭建成本高,即便这样也不能完全符合反应堆的真实情况,其可行性和可靠性都较差。数值模拟一般使用RELAP 5程序将反应堆简化为一维模型计算[9],虽然 RELAP 5 程序使用广泛,与已有的实验结果也能基本符合,但是其内置的 CCFL 模型中的关键参数需要用户输入,对于这些关键参数的研究还比较缺乏。本文使用RELAP 5程序对经典的简单数值管道中研究CCFL的Dulker实验台进行建模计算分析,以验证Wallis形式对CCFL模型的可行性,并分析注入不同的初始液相质量流量对CCFL现象的影响;然后以棒束通道为测试段的Karei实验为基础实验台进行建模,进一步探讨RELAP 5对棒束通道中CCFL现象的计算能力,以及适用于棒束通道的CCFL模型。

1 竖直管段内CCFL现象相间作用模型比较

由于不同结构处的气液两相相间作用机制差异较大,所以不同结构处CCFL现象的形成机理和表现形式也不相同,如发生水力突跃、形成波浪阻塞、液滴夹带甚至更剧烈的扰动等。研究CCFL现象的本质就是要研究气液两相相间作用机理,因此必须要对气液两相相间作用模型进行深入研究。目前在系统程序中广泛使用的CCFL模型主要有Wallis模型、Kutateladze模型和Bankoff模型,它们的通用结构为

(1)

式中:H——无纲量通量,下标g表示气相,下标f表示液相;

m——线性关系的斜率;

c——截距。

模型认为,在CCFL起始发生时,无量纲气液相流量的1/2次方满足线性关系,如图1所示。

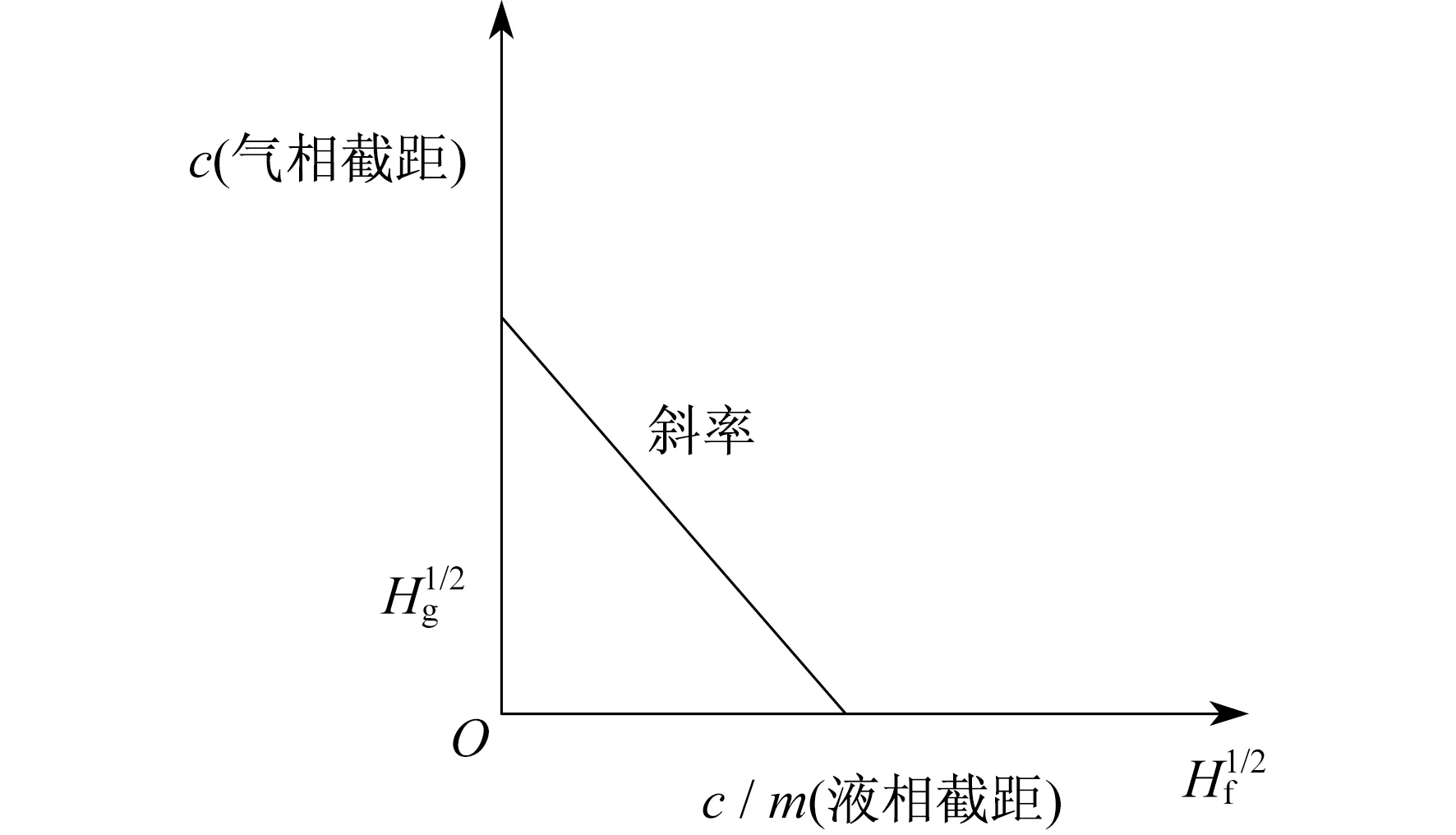
图1 CCFL模型无量纲气相与液相流量的关系

各个参数的具体计算公式如下。

(2)

(3)

w=D1-βLβ

(4)

(5)

式中:α——空泡份额;

v——速度;

ρ——密度,Δρ=ρf-ρg;

g——重力加速度;

w——长度尺寸;

D——水力直径;

L——拉氏毛细管长度常数;

σ——表面张力。

β取值在0～1之间。不同的取值代表不同的模型:β=0为Wallis 公式;β=1为Kutateladze公式(即Wallis认为该现象与水力学直径有关,而Kutateladze认为该现象与表面张力有关);0<β<1时,用户可依据Bankoff模型提出的建议进行输入[1],取值可以根据具体的几何结构进行选择。

2 不同模型的适用性研究

2.1 基于Dulker实验台的模型适用性研究

Dukler 实验台是经典的验证模型实验,实验可靠性高,因此本文使用 RELAP 5 程序对 Dulker 实验台进行建模分析,以验证 RELAP 5 程序对简单竖直管中 CCFL 现象的预测和计算能力,并且对 CCFL 模型中的参数选用进行优化。

2.1.1 Dukler实验台介绍及建模

Dukler实验台采用长为3.96 m和直径为0.050 8 m的管道进行气液两相CCFL现象试验,研究下落液膜与上升气流之间的相互作用[10]。Dukler实验回路如图2所示。

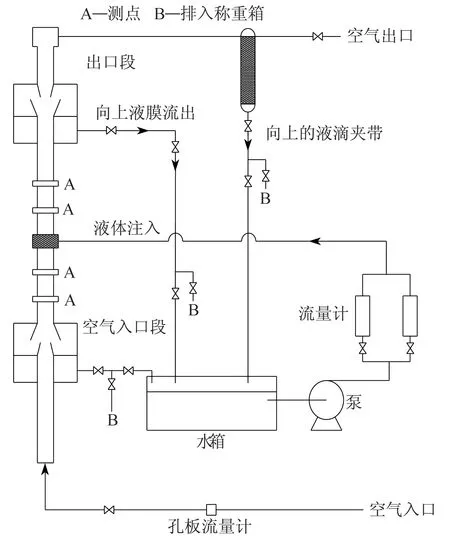
图2 Dukler实验回路示意

图2中,空气入口部分的设计是为了去除与空气流动方向相反的液体薄膜的下落,并为空气提供一个平滑的入口。入口由一个树脂玻璃管道组成,管道顶部有一个光滑的法兰连接到测试区域,底部有一个管道。在这一段下面是一根1.52 m长、0.050 8 m内径的有机玻璃管。为了防止入口的压力波动,液位必须保持恒定。下降的液膜通过一个膨胀喷嘴,使得液膜外径扩大。离开喷嘴后,液膜进一步展开,以避免与上升气流相互作用。

图3为RELAP 5程序模拟 Dukler 试验台的一维节点图。图3中:试验段包括PIPE 007,BRANCH 006,PIPE 005;PIPE 003用于平稳空气来流,减小入口扰动;空气从BRANCH 004注入测试管,流速由TDJ 002控制;液相从BRANCH 006注入,由TDJ 014控制流速;测试管流出液体从BRANCH 004 经PIPE 011排至水箱。在RELAP 5程序计算时,BRANCH 006-1选择使用 CCFL 模型的 Wallis 关联形式,用户输入模型参数为β=0,m=1,c=0.88。气液两相分别为空气和水。

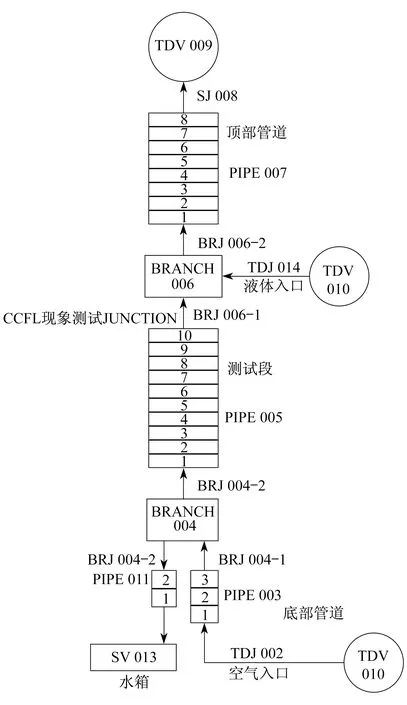
图3 Dukler实验台一维节点划分

2.1.2 计算结果分析

在Dukler的实验工况中,液相分别保持0.031 5 kg/s,0.063 0 kg/s,0.126 0 kg/s的质量流量从BRANCH 006向下注入;气相从管道底部注入,以0.000 067 kg/s2的速率线性增加。选用Wallis模型,通过RELAP 5程序对Dukler实验台进行计算。

图4 计算值与实验值的比较

由图4可以看出,选用Wallis模型时,对于液相注入质量流量较大的工况,测点A处气液质量流量的程序计算值与实验值非常接近;当液相注入流量较小时,程序计算值与实验值存在差异。

图5是使用CCFL模型,液相注入质量流量分别恒定为0.126 0 kg/s,0.063 0 kg/s,0.031 5 kg/s时,BRJ 006-1中液相质量流量随时间的变化对比图。

图5 不同液相注入下液相质量流量对比

由图5可以看出:随着气相质量流量的不断增加,液相质量流量起初保持不变;气相质量流量增加到一定程度时,液相质量流量会随之减小,这意味着CCFL开始发生;气相质量流量继续增加,流动振荡加剧,液相质量流量逐渐减小到零,流动停滞,甚至会出现液相反向流动的现象;液相注入质量流量越大,CCFL现象发生得越早,持续时间越长,液相流动停滞的时间也越晚。

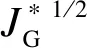
图6 选用CCFL模型时气液无量纲数的关系

图7 未选用CCFL模型时气液无量纲数的关系

由图6和图7可以看出:使用CCFL模型时,程序计算结果变化趋势与CCFL曲线通用形式基本吻合,但是m和c的值与所选Wallis模型有所差异,这可能是程序设置中一些用户自定义的参数选取问题所导致的,例如管道壁面摩擦因数。此外,在液相质量流量较小的区域出现不稳定的波动,不能完全与CCFL曲线吻合,说明程序对于低液相质量流量下CCFL现象的计算可能存在问题。

而不使用CCFL模型时,程序计算的值大多数超出了CCFL曲线的限制,低估了气液两相的相互作用,与实验结果相比差异较大。这说明必须通过CCFL模型对气液两相间的相互作用进行估计,以避免事故的发生。

通过对Dukler实验台实验数据和RELAP 5程序建模计算的对比可以得到:选用 RELAP 5程序的CCFL模型能够模拟气液相向流动限制现象,定性上符合实际物理过程,定量上基本能与试验相吻合;但CCFL模型系数选用有待进一步的优化。

2.2 基于Karei实验台的模型适用性研究

研究者们对于堆芯下降段中CCFL现象进行了多次实验,其中最为经典的实验台是 1989 年韩国原子能研究所(Korea Atomic Energy Research Institue,KAERI)对棒束通道的实验。KAERI 通过对棒束通道中的关键参数(如气液两相流量、空泡份额、压降)测量和程序计算结果对比分析,验证了 RELAP 5 程序对于棒束通道 CCFL 现象的计算能力,本文也使用 RELAP 5 程序对 Karei 实验台进行建模计算。

2.2.1 Karei实验台介绍及建模

使用 RELAP 5 程序对 Karei 实验台进行建模计算。首先验证程序对棒束通道 CCFL 现象计算的可用性,然后通过改变一些关键参数来探究 CCFL 模型中用户输入参数的影响因素[11]。实验采用常温常压下的水和空气进行。整个实验设备包括水和空气的供应设备,用于测试管段水和空气流量、差压,水位的传感器和测量工具,以及一些阀和泵等。整个测试管段如图8所示。

图8 棒束通道示意(mm)

管阵列具有与典型的17×17压水堆燃料管束相同的几何尺寸。实验在竖直棒束通道中模拟CCFL现象,下部充气室有两个入口,一个用于水,另一个用于空气。

整个实验过程为:打开水泵,水由顶部的水箱引入到测试管,并在流速控制器和传感器的控制下,模拟形成一种向下匀速流动的状态;空气由底部的进气室压出形成向上流动的气体,气体以一定的加速度不断增大,逐渐进入到测试段。

以入口液体的流速与时间的关系建模,有时RELAP 5模型会受到动量方程的影响,尤其是对气道的影响难以避免,因此需要特别注意采取建立单独节点的方式加以避免。将简单竖直管划分为6个控制体作为测试段,经过多次试验,发现将CCFL现象设置在JUN 004这一连接件上最合适。由于注气点和注液点的注入方式不同,气流注入时会产生曲线波动,所以实验时长的选择至关重要。经过反复试验和误差分析,发现300 s的持续时间可以完全忽略注入气流的曲线波动。

Karei实验台测试段的几何参数和边界条件如下:通道长度为1.5 m;边界压力为0.1 MPa;进口水温为282 K;进口气温为280 K;液体流量为0.04 kg/s;气相流量前10 s速度为0,10～200 s由0均匀增加到10 kg/s,后100 s均匀增加到20 kg/s。

RELAP 5程序建模节点图如图9所示。图9中:PIPE 003代表棒束通道;TDV 001和TDV 007分别是液体和气体的入口边界,分别从相反的方向注入,液体质量流量一直保持不变,气相质量流量逐渐增加;TDV 011和SV 009代表出口边界。

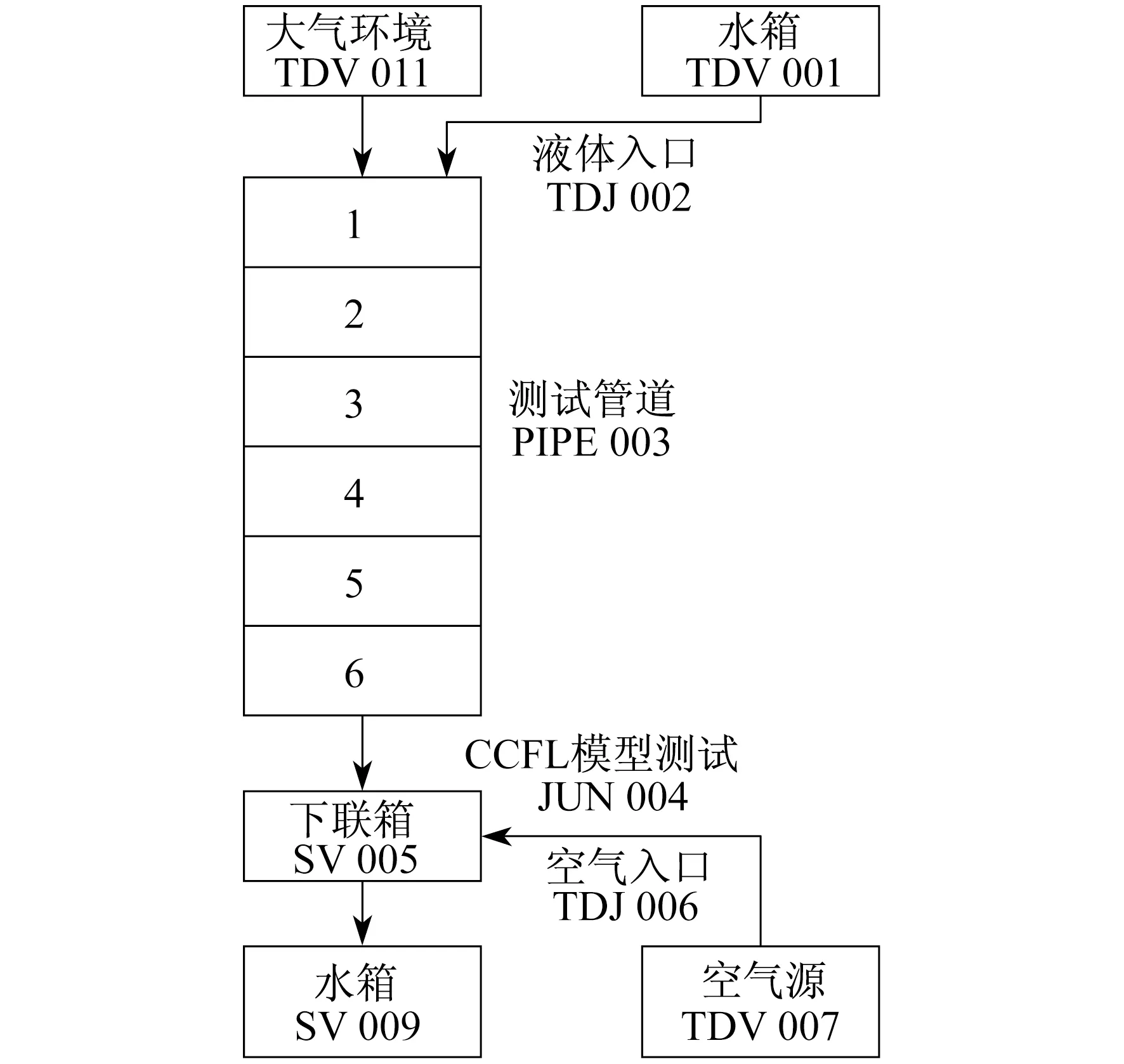
图9 实验台一维节点划分

2.2.2 计算结果分析

通过RELAP 5程序代码模拟计算,复现了实际实验的工况,通过对测试段的实验数据和计算结果的对比,分析程序中的CCFL模型对实际流动中CCFL现象的预测能力。JUN 004位于测试段末端,气液相互作用明显,因此本次模拟计算选择在JUN 004处开启CCFL模型,来探讨该模型对气液相间作用的影响。

在未开启CCFL模型时,气相质量流量在300 s内不断增加,直到完全发生CCFL现象。

液相质量流量的变化如图10所示。从图10可以看出,在110 s时,由于相间阻力的增大,液相向下流动受到限制,液相质量流量出现了小的波动,所以说明CCFL现象已经开始发生。

图10 未选用CCFL模型时JUN 004液相质量流量变化

利用计算得到的气液两相质量流量,通过式(1)计算出的气液两相表观速度无量纲数关系与实验数据对比情况如图11所示。

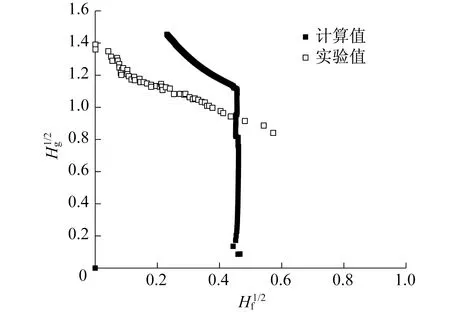
图11 未选用CCFL模型时气液表观速度无量纲数的关系

由图11可以看出,计算值曲线发生CCFL现象时的气相流量要明显高于实验数据。这意味着对高于程序计算值曲线的点来说,程序默认发生CCFL现象;对低于实验值曲线的点来说,程序默认不发生CCFL现象;但是对二者之间的点来说,实验值认为其发生CCFL现象,计算值却认为其不发生CCFL现象。这是由于程序未开启CCFL模型时,低估了气液两相的相间作用,而在真实的流动情况中,气体流量的变化对液相的流动会产生严重的影响。

当开启CCFL模型时,模型的形式以及关键的参数需要用户确定。当选择Wallis形式时,即输入β=0,m和c的值根据通流面积大小和以往的经验,选取m=1.0,c=0.88。这种情况下将计算结果与实验结果进行对比,结果如图12所示。

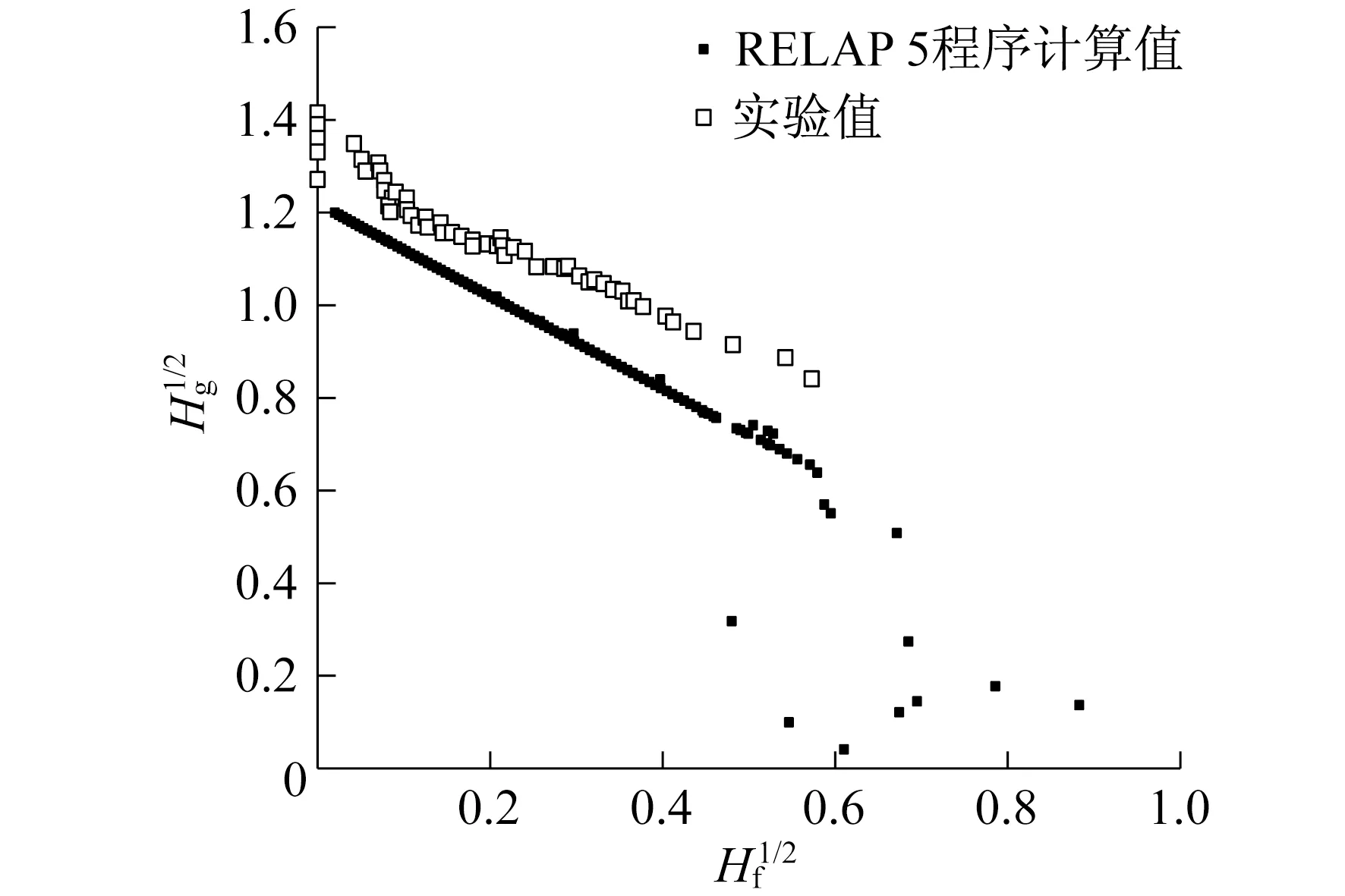
图12 选用Wallis形式CCFL模型时气液表观速度无量纲数的关系

由图12可以发现,开启CCFL模型后,程序计算结果绘制曲线的整体变化趋势与实验结果比较接近,但是Wallis模型计算结果中气液无量纲数曲线要整体低于实验值,意味着对高于程序计算值曲线的点来说,肯定不发生CCFL现象;对低于实验值曲线的点来说,肯定发生CCFL现象;但是对二者之间的点来说,实验值认为其没有发生CCFL现象,程序计算值却认为其发生CCFL现象。这与实际情况存在偏差。由此可以看出,选用Wallis形式的CCFL模型能大致预测CCFL现象的发生,但当气液两相流量在某些确定的范围内时,过于高估了气液两相之间的相间作用。

当选择Kutatekadze形式的CCFL模型时,输入β=1,m和c的值根据实验数据拟合,输入m=1.0,c=1.44,在这种情况下将计算结果和实验结果进行对比分析。液相质量流量的变化如图13所示。与未开启CCFL模型时(图10)相比,液相质量流量在90 s左右开始逐渐减小,到200 s时减为0,这说明开启CCFL模型后整个CCFL发生的时间都提前了。

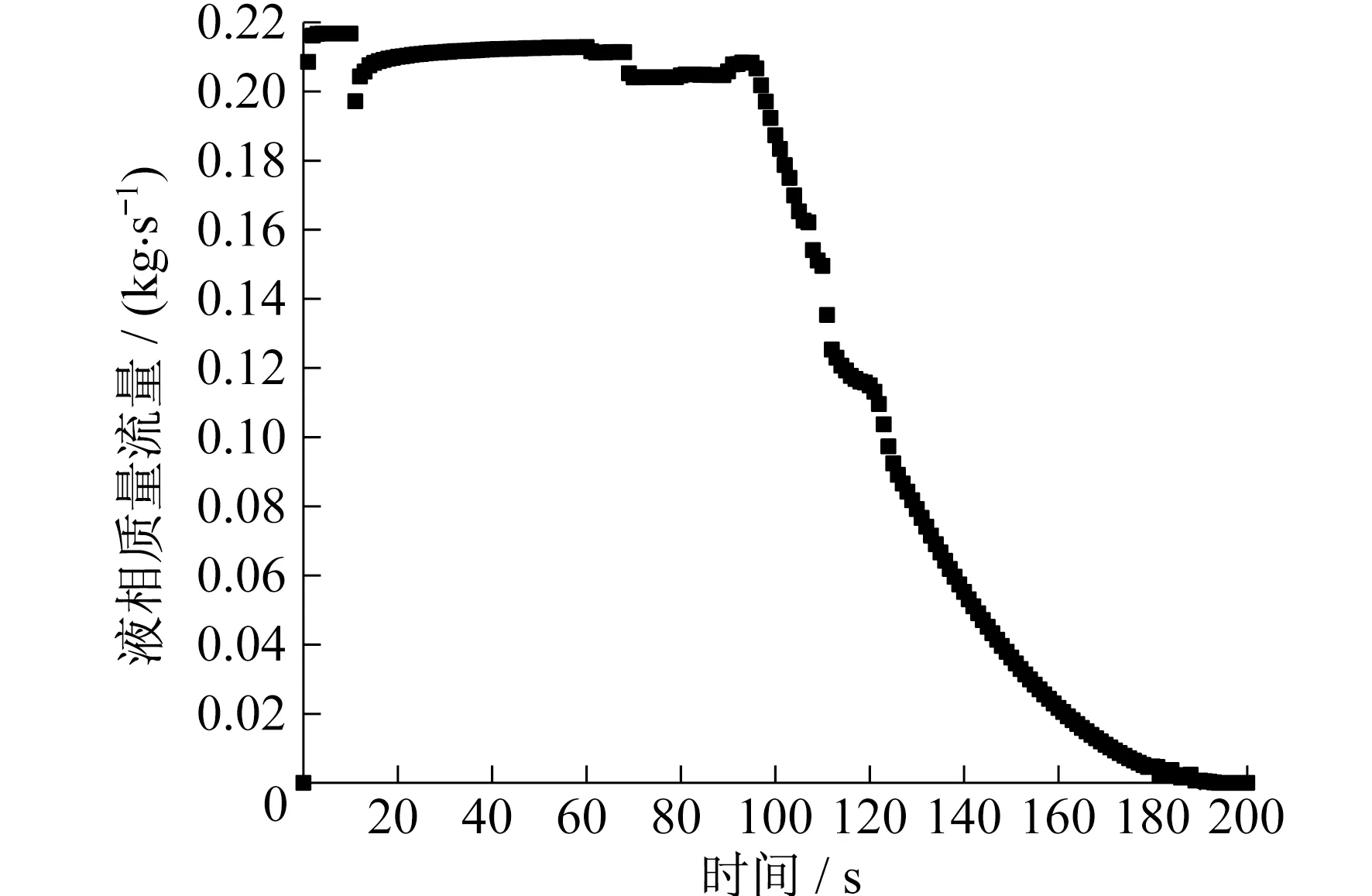
图13 选用Kutateladze形式CCFL模型时液相质量流量变化

通过程序计算出的气液质量流量的数据,根据式(1)拟合后的曲线如图14所示。由图14可以看出,程序计算值拟合出的气液表观速度无量纲数曲线与实验数据吻合较好,意味着程序能准确地预测和描述实验过程中的CCFL现象。

图14 选用Kutateladze形式CCFL模型时气液无量纲数的关系

通过对实验数据和程序计算结果的对比分析,可以验证RELAP 5程序对棒束通道内CCFL现象有一定的计算能力,但是对于不同初始液相流量对CCFL产生的影响还尚不明确,因此选取不同初始液相流量KL分别为0.01 kg/s,0.05 kg/s,0.08 kg/s对CCFL模型进行进一步验证。对比结果如图15所示。

由图15可以看出,不同的初始液相流量对CCFL现象发生的时间有影响,在保持气相流量一致的情况下,初始液相流量越小,CCFL现象发生得越早;但是无论初始液相流量怎么变化,计算结果都能很好地与CCFL曲线吻合,说明对于棒束通道来说,初始液相流量不是影响CCFL现象形成机理的主要因素,只是会影响CCFL发生的时间。由于Kutateladze形式的CCFL模型主要考虑表面张力的影响,所以可以推断棒束通道内中CCFL现象的出现与表面张力有关。

图15 不同初始液相流量时气液表观速度无量纲数的关系

3 结 论

(1) 针对经典的简单竖直管中CCFL研究的Dukler实验台的建模分析表明,使用Wallis形式的CCFL模型时,能很好地预测CCFL现象的发生。此外,在气相质量流量一定的情况下,初始液相质量流量越大,CCFL发生的时间就越晚。

(2) 以Karei实验为建模基础,进一步探讨RELAP 5程序对棒束通道中CCFL现象的计算能力和适用于棒束通道的CCFL模型。结果表明,使用Wallis形式的CCFL模型时,计算结果的整体趋势与实验数据一致,但是在一定范围的气液质量流量内,计算结果与实验数据呈现了不同的结果;使用Kutateladze形式的CCFL模型时,计算结果能很好地与实验数据吻合,说明Kutateladze形式的CCFL模型更适用于棒束通道。