基于层次分析法的商品装袋顺序综合评价模型探析

文/陆惠敏 冯慧茹 毕以霖 任思沅 王浬力（天津商业大学理学院）

从19世纪以来，零售行业一共经历了四个发展阶段[1]: 第一阶段是百货公司的兴起；第二阶段是连锁超市、便利店等业态的出现；第三阶段是C2C电子商务的飞速发展；第四阶段是线上线下的交互融合阶段，即新零售阶段。随着互联网、物联网、大数据和云计算等新一代信息技术的发展，电子商务也产生了更多的变化，无人超市的出现也是对传统零售方式的进一步提升[2]。无人超市挑战了传统的零售行业，逐渐成为当前零售行业的宠儿，线上与线下深度经营的“智能零售”不只是无人超市的代名词，更是衍生多元形态的契机[3]。无人零售，可以结合生物识别、计算机视觉、先进算法、移动支付等技术产业，改变传统零售业的服务模式和销售模式，采用更加智能化的方式降低人员成本，提高管理效率。

“24爱购”就是一家基于互联网应用的智能便利店，用户仅需在“24爱购app”或“24爱购微信小程序”进行选货、付款、下单，然后由自动取货系统将购买的物品取出，直接放入取货柜中，用户在24小时以内打开放置自己物品的格子门，直接拿走即可完成整个全自动化购物的闭环。但是纵观整个全自动化购物过程，其中并没有装袋环节，商品只是零散地放在取货柜的格子里，同时用户在取货时还要自带购物袋，这给自动化购物带来了取货时的不便，也降低了用户的体验感。为了解决自动化装袋环节中商品摆放顺序的问题，本文采用了层次分析法进行深入探究。

层次分析法（AHP）是一种将与决策有关的不同指标一一列出，设置目标层、准则层、方案层等不同的层次，通过对目标问题的固有本质、影响因素及其内在的关联进行分析，得到各个指标的权重，从而为繁复的决策问题提供简单的决策方法[4]。实际的装袋问题需要从多指标角度进行比较，直接建立靠近实际生活的模型会比较复杂且困难。因此选择层次分析法作为建立模型的基础，可以将复杂的问题简单化，在得到简单实用的决策方法的同时，还可以得到所有商品的不同指标对某个商品在装袋顺序中的影响程度，即不同指标在模型中的权重，从而确定商品在装袋过程中的先后顺序。故在研究商品排序问题时，利用层次分析法将会有着较为良好的效果。因此本文将选取“24爱购”的30种商品模拟超市购物流程，利用层次分析法，建立装袋顺序综合评价模型，随机抽取商品，对商品序列进行排序，从而得到自动化装袋顺序。

一、装袋顺序综合评价模型

构建装袋顺序综合评价模型的目的在于综合顾客购物结束后装袋环节的多维度评价指标，从而得到商品装袋顺序。在综合评价模型中，评价指标是商品的属性，是整个模型的基础；评价目标是通过模型得到各商品的综合评价得分，比较得分大小确定商品装袋顺序。

（一）综合评价模型的建立

通过对商品相关属性的研究以及对若干顾客的问卷调查结果，顾客在装袋过程中会考虑商品的各种因素，将这些因素归结为五类属性，即耐压程度X1、易碎程度X2、易融程度X3、重量X4、体积X5，基于层次分析法确定各属性对装袋顺序的权重系数ωi，计算得出综合评价得分Y。基于参考文献[5]本文建立了综合评价模型，可表示为：

（二）商品属性值

选取30种商品模拟超市购物流程，对商品的5类属性进行赋值，取值范围为1～9。X1为商品的耐压程度，数值越高代表越耐压；X2为商品的易碎程度，数值越高代表越不易碎；X3为商品的易融程度，数值越高代表越不易融；X4为商品的重量，数值越高代表商品越重；X5为商品的体积，数值越高代表体积越大。这30种商品的属性值如表1所示。

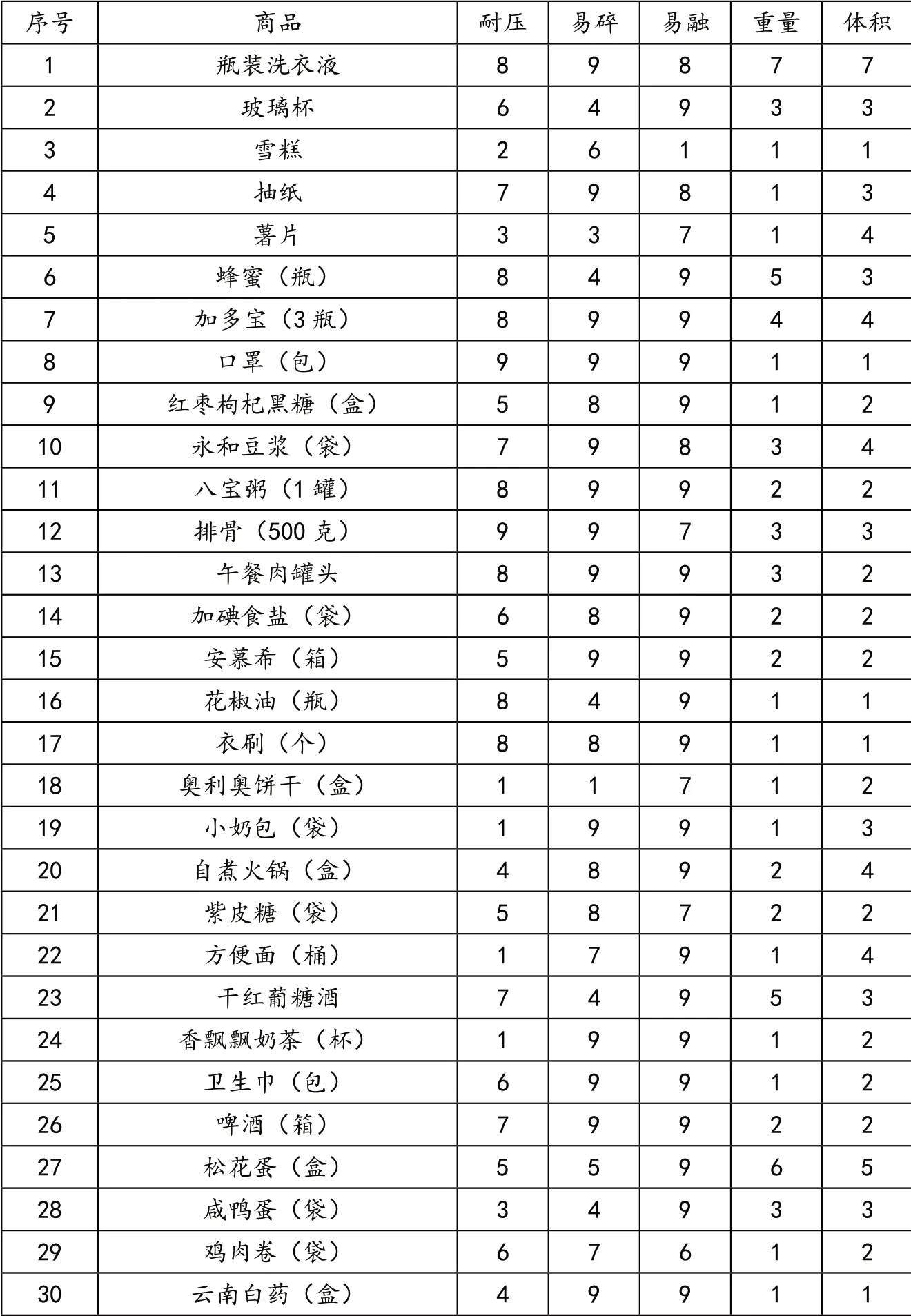
表1 商品属性值

二、综合评价模型求解及结果分析

（一）建立层次结构模型

根据耐压程度、易碎程度、易融程度、重量和体积等指标进行综合评价并作出决策，以瓶装洗衣液、玻璃杯、抽纸、雪糕、薯片为例建立层次结构模型如图1所示。

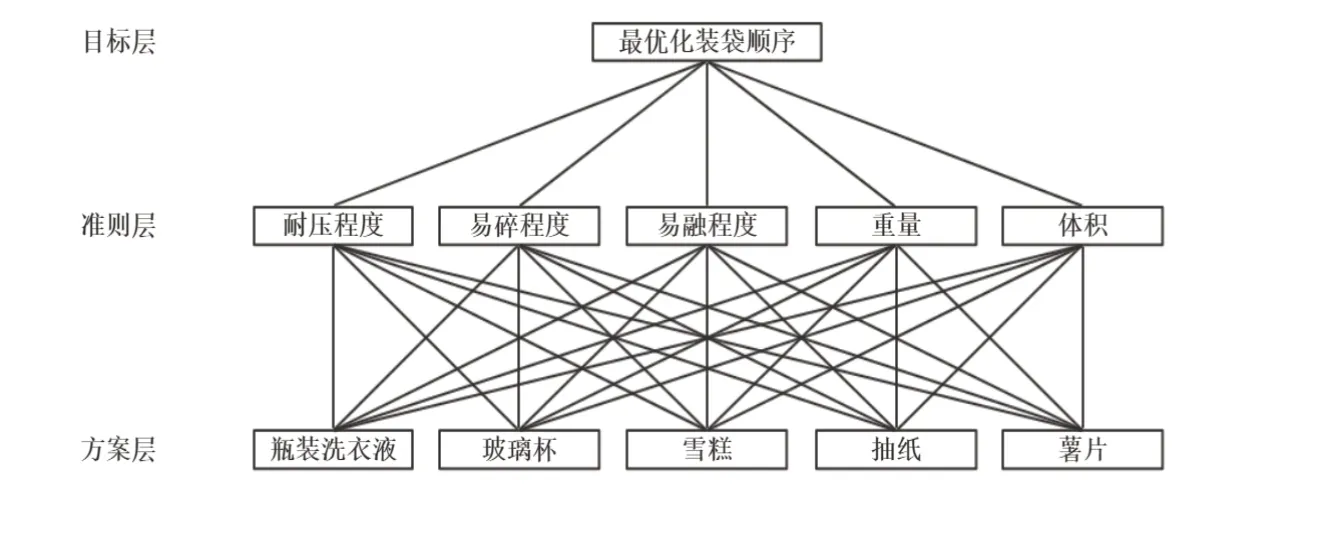
图1 商品装袋顺序层次结构图

（二）构造判断矩阵

用Santy的1～9标度法比较同一层两两指标间相对重要程度，如表2所示：

表2 构造判断矩阵的1～9标度法

构造判断矩阵：X=(Xij)5×5

由表2可知：

因此，判断矩阵X为正互反矩阵，并且X的元素具有传递性，即满足：

所以X为一致性矩阵。

1.考虑准则层对目标层的重要程度，顾客会权衡这些准则在自己心中占多大比重，这里根据耐压程度、易碎程度、易融程度、重量、体积设计调查问卷，得到判断矩阵X如图2所示。

图2 判断矩阵X

2.考虑耐压程度(X1)，对5种商品的耐压程度进行比较，构造判断矩阵B1如图3所示。

图3 判断矩阵B1

3.考虑易碎程度(X2)，对5种商品的易碎程度进行比较，构造判断矩阵B2如图4所示。

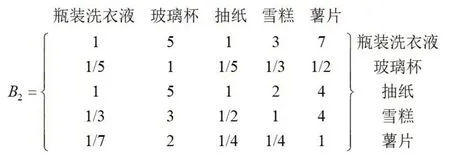
图4 判断矩阵B2

4.考虑易融程度(X3)，对5种商品的易融程度进行比较，构造判断矩阵B3如图5所示。

图5 判断矩阵B3

5.考虑重量(X4)，对5种商品的重量进行比较，构造判断矩阵B4如图6所示。

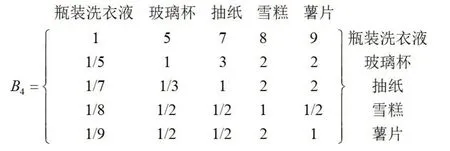
图6 判断矩阵B4

6.考虑体积(X5)，对5种商品的体积进行比较，构造判断矩阵B5如图7所示。

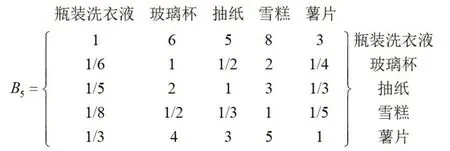
图7 判断矩阵B5

（三）层次单排序与一致性检验

1.准则层对目标层

（1）计算权重向量

利用MATLAB进行计算得到耐压程度、易碎程度、易融程度、重量、体积这5个因素相对于目标的权重向量为。

W=（0.4386,0.1412,0.0657,0.296 00.0585）T

权重向量反映了耐压程度对装袋顺序的影响最大，其次是重量，再次是易碎程度和易融程度，最后是体积。

（2）一致性检验

由线性代数知识可知：n阶正互反矩阵X为一致性矩阵的充分必要条件是其最大特征值λmax=n。基于此结论，对上述判断矩阵进行一致性检验[6]的步骤如下：

第一步：计算一致性指标

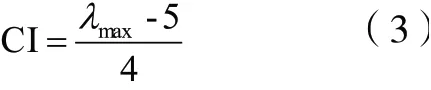
显然，CI值越接近于0，X的一致性越强；反之，一致性越弱。

第二步：计算随机一致性指标：RI

为衡量CI的大小，引入随机一致性指标R，随机构造1000个两两比较矩阵X1，X2，…X1000计算它们的一致性指标CI1，CI12，…，CI1000则相应的随机一致性指标为：

常用的1～16阶正互反矩阵的随机一致性指标值如表3所示。

表3 1～16阶正互反矩阵的随机一致性指标值

当CR＜0.1时，认为判断矩阵的一致性是可以接受的，否则需要对判断矩阵作适当修正。通过MATLAB计算得X的最大特征值为λmax=5.3523，一致性指标为CI=0.0881，一致性比率指标CR=0.0786＜0.1，这表明判断矩阵X通过了一致性检验。MATLAB代码如下所示：

2.方案层对准则层

通过MATLAB计算得出结果如表5所示，显然，B1，B2，B3，B4，B5均通过了一致性检验。

MATLAB代码如下所示：

（四）层次总排序与决策

方案层对目标层的组合权重(各方案得分)记为：

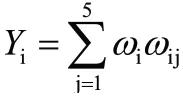
在层次单排序与一致性检验中，设方案层对准则层中的第j个因素Xj的层次单排序一致性指标为CIj，则层次总排序的一致性比率为

由MATLAB结 果 可 知CR=0.0346<0.1，说明层次总排序通过了一致性检验。层次总排序的组合权重为Y=(0.5094，0.1831，0.1575，0.0760，0.0741)T，因此装袋顺序为：瓶装洗衣液→玻璃杯→抽纸→雪糕→薯片。MATLAB代码如下所示：

表4 层次单排序的权重向量和一致性检验结果

（五）确定装袋顺序

1.将权重向量带入综合评价模型得：

计算得到Y=(7.7867,6.0352,5.63 41,3.1529,2.4991)，最终的装袋顺序为：瓶装洗衣液→玻璃杯→抽纸→雪糕→薯片。综合评价模型得出的结果与层次分析法得出的结果一致，充分证明了模型的可靠性和准确性，因此该综合评价模型可用于商品装袋顺序的模拟。

2.通过R代码进行购物模拟

利用R软件进行5次顾客购物模拟，每次从30种商品中随机抽取10种商品确定装袋顺序，R代码（“数据.csv”来源于表1）如下所示：

运行代码得到5次模拟的结果如图8-12所示：

图8 第1次模拟结果

第一次模拟装袋顺序为：瓶装洗衣液→口罩→衣刷→加碘食盐→卫生巾→紫皮糖→鸡肉卷→红枣枸杞黑糖→方便面

第二次模拟装袋顺序为：加多宝→八宝粥→永和豆浆粉→啤酒→玻璃杯→紫皮糖→红枣枸杞黑糖→自煮火锅→小奶包→方便面

第三次模拟装袋顺序为：午餐肉罐头→永和豆浆粉→干红葡萄酒→衣刷→抽纸→加碘食盐→花椒油→鸡肉卷→自煮火锅→雪糕

第四次模拟装袋顺序为：排骨→午餐肉罐头→蜂蜜→口罩→松花蛋→花椒油→卫生巾→玻璃杯→鸡肉卷→云南白药

第五次模拟装袋顺序为：瓶装洗衣液→排骨→蜂蜜→八宝粥→干红葡萄酒→安慕希→小奶包→薯片→奥利奥饼干

由此可知5次模拟结果与日常装袋的顺序基本一致，充分说明模型具有可行性和准确性。

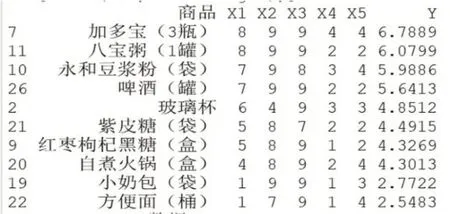
图9 第2次模拟结果

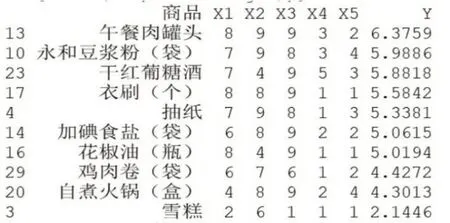
图10 第3次模拟结果

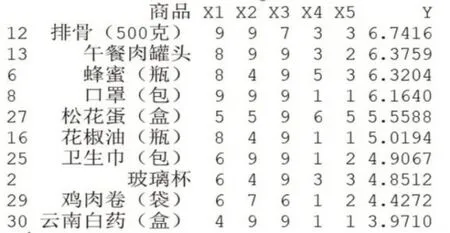
图11 第4次模拟结果

图12 第5次模拟结果

三、结论

本文利用了层次分析法对商品的五类不同指标进行评价，得出了指标值对决策的影响力大小，评价过程中构造的判断矩阵经过了一致性检验，说明判断结果是可以接受的。利用权重值给出综合评价模型，并随机选取不同类型的商品来验证模型的正确性，从而得到一个较为合理的商品装袋顺序模型，这为无人超市自动化装袋的整体过程提供了新思路。本模型存在一定的局限性，比如层次分析法具有主观色彩，商品选择有限，不适用于散装称重商品，因此商品装袋模型仍需进行优化。