基于改进型极限学习机的电子鼻气体浓度检测*
王 洁,陶 洋,梁志芳
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引言
电子鼻是一种仿生嗅觉系统,由气体传感器阵列和模式识别算法组成,主要用于气体识别[1],在环境监测[2]、食品检测[3]和医疗诊断[4]等多个领域均有所应用。电子鼻系统通过其内部的气体传感器阵列对气体信息进行采集,将气体信号转变为电信号,再通过模式识别算法的处理输出对应气体的浓度检测结果。
针对电子鼻模式识别系统,目前提出了多种网络模型,其中极限学习机是由黄广斌提出的一种典型单隐层前馈神经网络(Single-hidden Layer Feedforward Networks,SLFN)[5],与其他神经网络(BP 神经网络[6]、支持向量机[7](Support Vector Machine,SVM))相比,其结构简单,不需要反复迭代,学习速度快,泛化性能好,具有良好的函数逼近能力,因此被广泛应用于解决各种分类和回归的问题。但由于ELM 输入层与隐含层的权值以及隐含层的阈值是随机给定的,这将会降低网络模型对浓度的检测精度。
针对目前电子鼻在检测气体浓度精度不高的问题,本文利用粒子群算法的局部搜索能力和人工蜂群算法的全局搜索能力,将两个算法进行嵌入融合,并与极限学习机相结合,最终达到提高电子鼻气体浓度检测精度的目的。
1 基于PSOABC-ELM 的检测算法
本文结合粒子群算法[8](Particle Swarm Optimization,PSO)模型简单、局部搜索能力强和人工蜂群算法[9](Artificial Bee Colony Algorithm,ABC)种群丰富、全局搜索能力强的优点,提出一种PSOABC-ELM 算法。其具体思想是,以PSO 算法为主框架,结合ABC 算法中改进的跟随蜂和改进的侦察蜂阶段来提高粒子群算法的全局搜索能力。在该混合算法中,生成一个初始解,并计算每个个体的pbest。还增加了3个控制参数(pbestMeasure、Limit1 和Limit2),以确定执行算法的哪个阶段。pbestMeasure用于通过记录pbest 在迭代期间是否更新来管理种群中的个体,通过比较pbestMeasure的值与Limit1 和Limit2 的大小,来判断计算粒子新位置所采用的算法模型。重复迭代,通过不断更新粒子的位置,直至达到最小误差或者最大迭代次数终止,得到算法的最优解,将最优解作为ELM 神经网络的输入层与隐含层的权值和隐含层的阈值,降低随机给定权值阈值带来的误差。流程图如图1 所示,算法具体步骤如下:
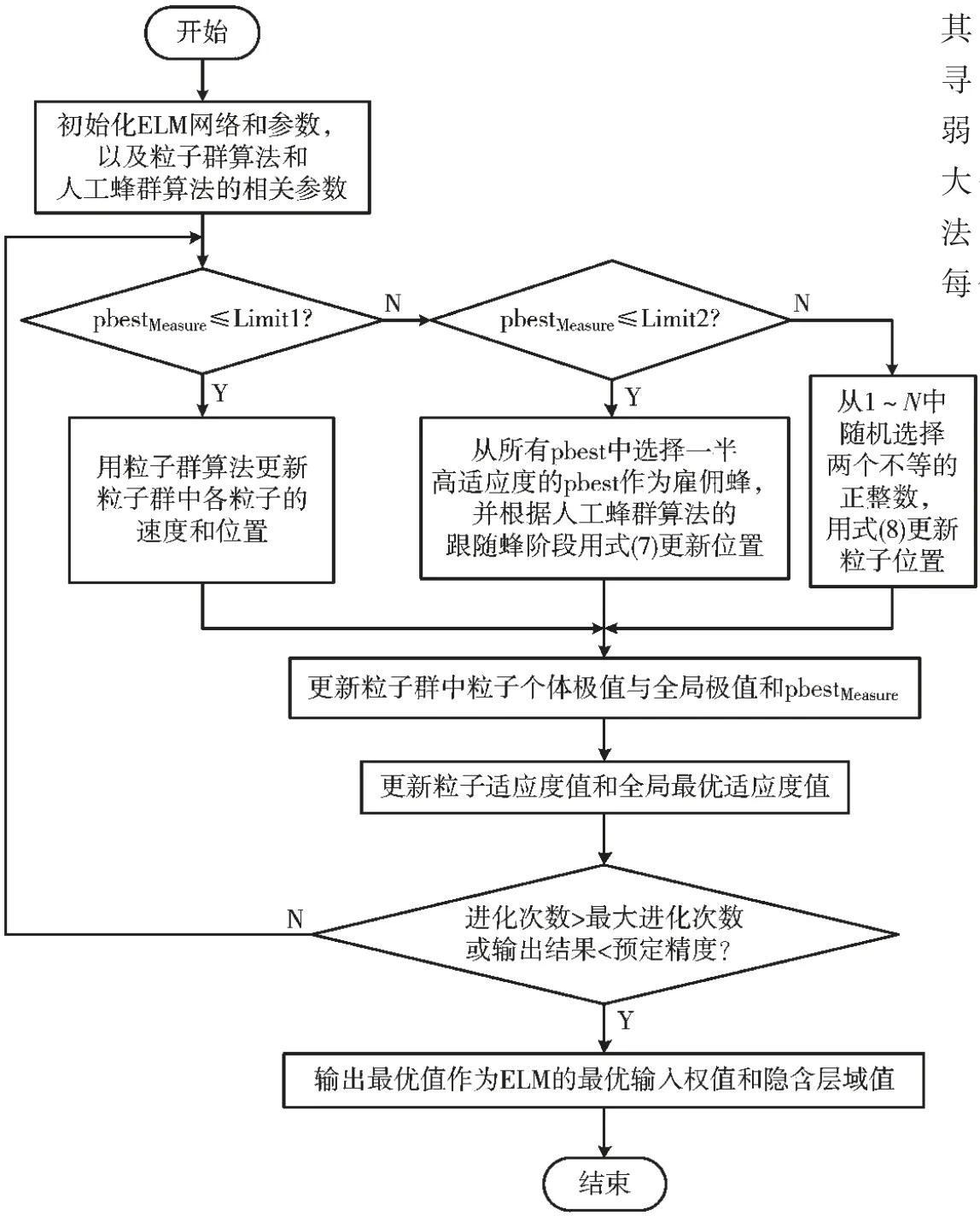
图1 PSOABC-ELM 算法流程图
(1)确定神经网络拓扑结构。得到具有n 个输入层节点、l 个激活函数为g(·)的隐含层节点、m 个输出层节点的ELM;形成N 个任意不同的维度为D 的训练样本集,随机产生输入层与隐含层的权值和隐含层的阈值。
(2)参数初始化。对粒子群算法和人工蜂群算法中所有参数初始化,同时计算控制参数Limit1 和Limit2,其中l1=0.01,l2=0.05;并将控制参数pbestMeasure初始化为0。

(3)选择适应度函数。本文选用均方误差作为最佳适应度函数,适应度值越小,个体越优秀。
(4)将处理后的数据输入模型,根据pbestMeasure判断当前个体执行哪个阶段。
①当pbestMeasure(i)≤Limit1,用传统的PSO 算法得到最优个体对应的粒子位置,算法的核心是对粒子的速度x和位置v 进行更新,其更新公式如下:

其中,ω 称为惯性因子,其值为非负,其值较大时,全局寻优能力强,局部寻优能力弱;较小时,全局寻优能力弱,局部寻优能力强[10];ωmax和ωmin分别为惯性权重的最大值和最小值,通过将ω 调整为一个合适的值,使得算法的全局寻优能力和局部寻优能力达到一个平衡;c1为每个粒子的个体学习因子,c2为每个粒子的社会学习因子,通常取c1=c2=2;r1和r2是[0,1]内均匀分布的随机数,可增加搜索随机性;Pid表示第i 个变量的个体极值的第d 维,Pgd表示全局最优解的第d 维。通常将位置和速度限制在[-xmax,xmax]、[-vmax,vmax]。
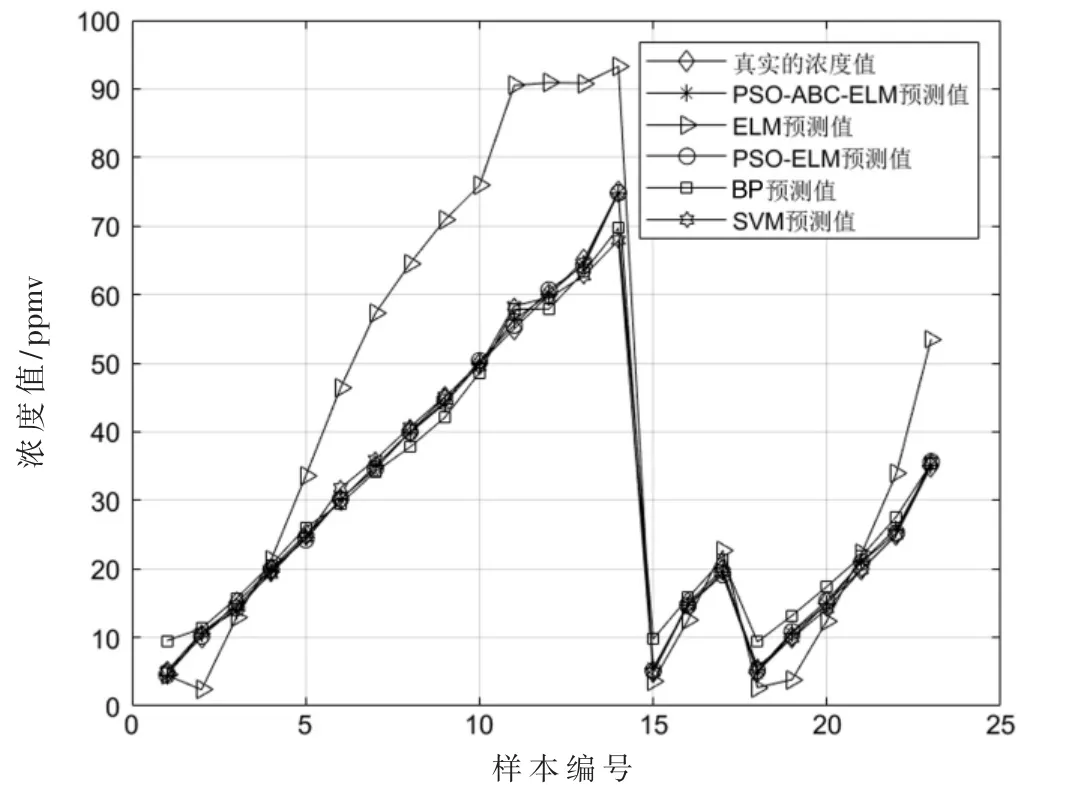
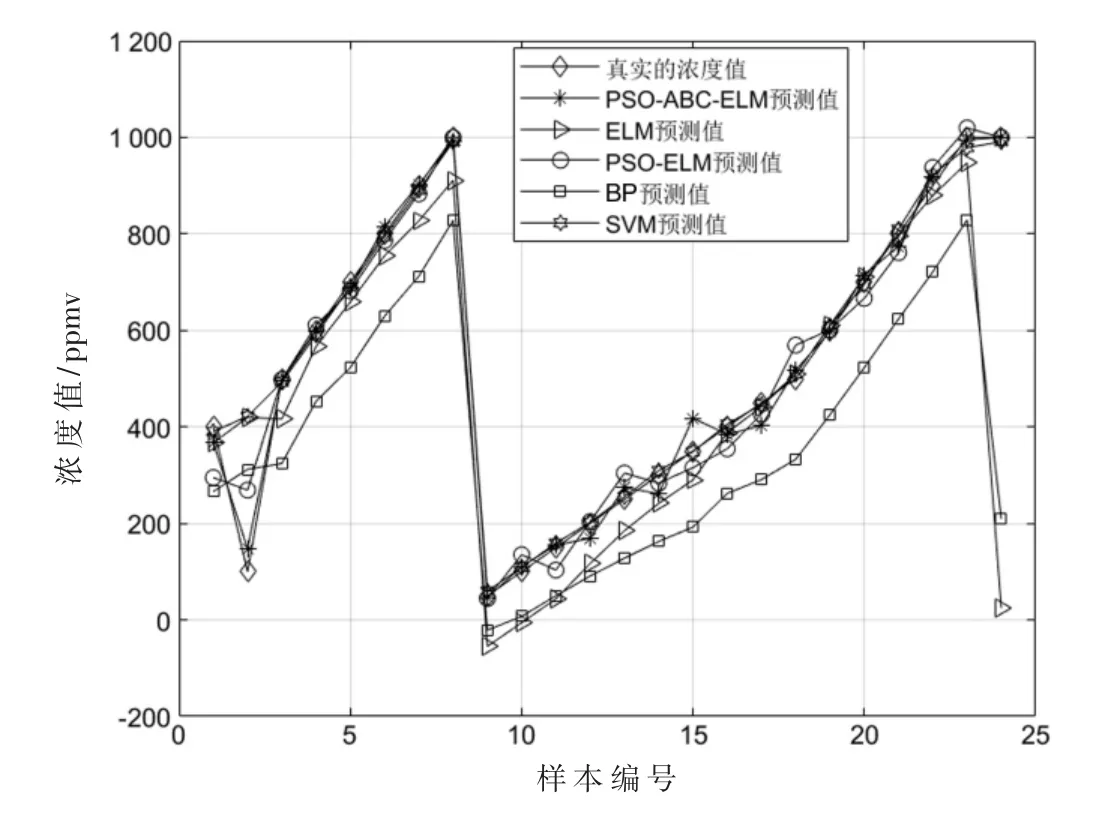
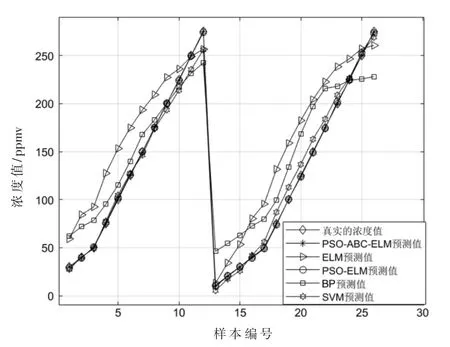
②如果Limit1 式中,fitness(xi)为第i 个跟随蜂的适应度值,pi为第i 个跟随蜂被选择的概率,SN 为蜜源数。一旦跟随蜂被选择,用式(6)计算通过贪婪算法选择第i 个跟随蜂原位置和新位置最优值,得到新的粒子位置; ③如果pbestMeasure(i)≥Limit2,从{1,2,…,N}中随机选择两个正整数k1≠k2≠i,用式(7)计算通过贪婪算法选择最优值得到新的粒子位置: 得到新的粒子位置后,更新粒子个体极值pbest 和全体极值gbest,如果更新了pbest 的值,则pbestMeasure的值设置为0,否则pbestMeasure将增加1。 对算法进行重复迭代,通过不断更新粒子的位置,直至达到最小误差或者最大迭代次数终止,得到算法的最优解,将最优解作为ELM 的最优输入权值和隐含层阈值。 (5)用训练的模型对测试集进行检测,并将检测结果与真实值进行比较,得到两个值之间的误差,通过对比误差得到结论。 该研究使用的数据来自加州大学欧文分校(University of California Irvine,UCI)机器学习数据库,数据集为不同浓度下气体传感器阵列数据集。该数据集收集了分别来自16 个化学传感器的6 种不同气体不同浓度的测量数据,这些数据提供了有关传感器在每次测量中暴露的浓度水平信息,可用于分析传感器回归问题[11-12]。 为充分验证本文提出的算法的有效性,本文选择BP 神经网络[13]、SVM神经网络[14]、ELM神经网络[15]、PSO-ELM[16]神经网络作为对比算法。实验基于这4 种对比算法以及本文提出的PSOABC-ELM 算法对传感器收集到的污染物气体进行浓度检测,为得到更好的网络检测性能,首先对高维的原始数据进行归一化处理,再利用主成分分析法(Principal Component Analysis,PCA)对数据进行降维,通过大量实验验证,最终确定提取6 个主成分数据作为电子鼻模型的输入数据。各模型参数设置如表1 所示。 表1 各模型参数设置 对各算法进行多次实验取平均值,各算法的检测效果可以由统计平均绝对误差(MAE)、均方根误差(RMSE)、相关系数(R)衡量,结果见表2,检测结果分别如如2~图7所示,其中图横坐标为样本编号,纵坐标为样本对应的气体浓度值,单位为ppmv。 图7 甲苯预测值与真实值结果对比 实验设置下各算法对不同气体的浓度检测效果如表2所示。通过表2可知,BP、SVM、ELM、PSO-ELM、PSOABC-ELM 算法对6 种污染物浓度检测结果与监测值的R 平均值分别为0.853 9、0.987 8、0.901 3、0.994 2、0.998 4,其中PSOABC-ELM 算法对6 项污染物的R 值均达到了0.99 以上。 表2 实验设置下各算法对不同气体的浓度检测效果比较 图3 乙烯预测值与真实值结果对比 图4 氨预测值与真实值结果对比 图5 乙醛预测值与真实值结果对比 图6 丙酮预测值与真实值结果对比 对比5 种算法对6 种气体的MAE 和RMSE,每种气体中PSOABC-ELM 的MAE 和RMSE 均为最低值,这意味着PSOABC-ELM 检测值与真实的浓度值最接近,拥有最佳检测效果。PSOABC-ELM 对6 种气体的MAE 除了氨的MAE 大于2 外,其余气体的MAE 均小于2。 为方便跟踪每类气体浓度的检测值与真实值之间的差异,图2~图7 分别给出了这6 种气体通过这5 种算法获得的气体浓度检测值与真实浓度值的跟踪曲线。由图可知,5 种算法对6 种气体的浓度检测值均可以较好地反映出污染物浓度变化的趋势,其中PSOABC-ELM对于6 种气体检测结果均与监测值基本拟合。 图2 乙醇预测值与真实值结果对比 综上可知,PSOABC-ELM 算法检测精度高,性能稳定可靠,应用PSOABC-ELM 算法的电子鼻系统可以成功地对空气污染物浓度进行检测。 本文针对电子鼻应用于气体污染物浓度检测时难以达到理想精度的问题,提出了一种PSOABC-ELM 算法,对电子鼻模式识别模块进行改进,并将其与BP、SVM、ELM 和PSO-ELM 算法进行比较。仿真结果表明,本文提出的算法有效提高了电子鼻对气体浓度检测的精度和可靠性。但其在气体浓度短时间内变化范围较大时误差会变大,今后的工作将针对本文提出的算法进行改进,提高在短时间内对变化范围较大的气体浓度检测精度,扩展应用范围。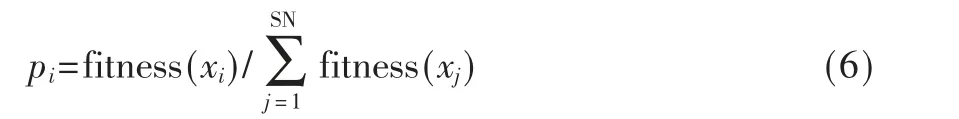

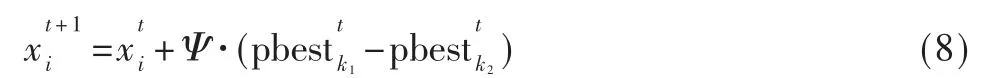
2 实验仿真及结果分析
2.1 实验数据集介绍
2.2 实验设置与仿真

2.3 实验结果分析




3 结论

