基于MIKE21水动力模型计算感潮河段闸下水位流量关系

王新强

(1.福建省水利水电勘测设计研究院，福州 350001；2.福建省水动力与水工程重点实验室，福州 350001)

1 概述

闸下水位流量关系计算作为水利水电工程设计中的关键性基础工作，具有非常重要的作用。在水利水电工程规划设计中，遇到设计断面附近无实测水位、流量或者实测资料不足的情况时，常常采用多种方法在水文调查和临时测流的基础上拟定水位流量关系[1-3]。目前，针对水位流量关系的研究较多，宋运凯等采用正交多项式和幂函数法计算得到春河伊春站水位流量关系[4]；梅立庚利用水力学法，采用一维恒定非均匀渐变流计算得到断面水位流量关系[5]；杨晓华等在研究自适应加速遗传算法求解的基础上得到水位流量关系[6]。李玉荣等通过对比三峡水库建库前后主要水文站实测资料，研究了三峡水库建库前后荆江低水水位流量关系[7]；张英骏等用密集的数据替代数学公式的模式,由计算机对收集的尽量多和新的实测水位流量数据两两直线内插后加权平均,直接得到推流流量结果,即无线推流方法[8]；程雪源等利用Excel拟合求解河流水位-流量关系曲线，提高了水流-流量关系曲线拟合的质量以及精度、效率等[9]；王浩以感潮河段水位预报作为研究对象，从河道洪水演算水文学的方法出发，综合考虑感潮河道洪水运动的基本特征，河道水位流量转换的基本方程等，研究出一种适用于感潮河段的水位预报方法[10]。

一般而言，水位流量关系指的是河道中某一横断面的流量与同时点水位之间的对应关系，一般以水位为纵坐标、流量为横坐标的水位流量关系曲线来表示，也可以选取适当的数学方程式，并根据曲线和数学方程式列出便于查读的水位流量关系表[12]，传统水位流量关系拟合方法计算比较方便，但是对于水流条件较为复杂的河道计算精度不高，尤其是河口感潮段河流，同时受径流和潮流共同作用，水流往复运动，闸下水位流量关系不易准确确定，本文根据木兰溪实测地形以及水文条件，利用MIKE21 软件建立木兰溪下游二维水动力数学模型，能够根据设计需要，模拟计算感潮段水闸下泄不同流量分别与高、低潮位遭遇的情况，得到闸下水位流量关系。

2 MIKE21 水动力模型

2.1 控制方程

MIKE21 水动力数学模型基于Navier-Stokes方程[11]。

具体控制方程如下：

(1)

(2)

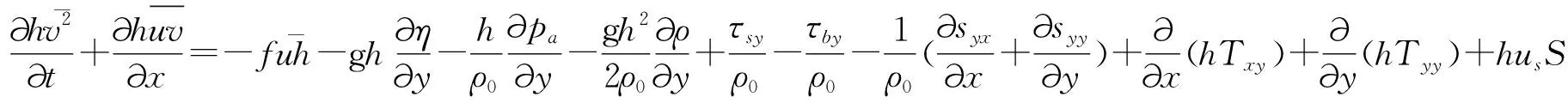
(3)

式中:

t——时间；

x,y——笛卡尔坐标系坐标；

η——水位；

d——静止水深；

h——总水深，h=η+d；

u,v——x,y方向上的速度分量；

f——Coriolis系数，f=2ωsinφ，φ表示所在地纬度，ω是指地球自转的角速度；

g——重力加速度；

ρ——水的密度；

sxx、sxy、syy——辐射应力的分量；

S——源汇项；

Txx、Txy、Tyx、Tyy——水平粘滞应力；

us,vs——源汇项的不同方向的水流速度。

2.2 求解方法

本次水动力数值模拟计算所用模型在空间上进行有限体积法离散，该方法将空间划分为不重复的控制单元，能够保证水动力模型中水量和动量守恒，模型在时间上的离散方法为显性欧拉法[12]。 二维浅水方程积分形式一般可以写成如下：

(4)

式中：

U——守恒变量的向量；

F——通量向量函数；

S——源项向量。

在Cartesian 坐标中，可以将上面的二维浅水方程表示成如下形式：

(5)

式中：

I——无粘性通量；

V——粘性通量。

3 模型建立与验证

3.1 模型建立

为了能够使模型计算结果更加合理、准确，本次水动力数学模型采用非结构网格对模型进行划分，模型的上边界定于木兰陂，并且考虑兴化湾江阴岛位置的潮位过程不受木兰溪洪水流量的影响，将数学模型建模下边界建至外海江阴岛，基于2007年实测地形进行验证计算，基于2010年1月实测地形进行工程计算，河道边界为防洪堤线(如图1所示)。

图1 木兰陂—江阴岛网格分布示意

3.2 模型相关参数

本次水动力数值模拟计算采用的参数主要有河道干湿边界、河道糙率、涡粘系数以及时间步长等。

模拟中设定完全湿单元与完全干单元的水深阈值分别为0.1 m与0.005 m，即水深大于0.1的单元为完全湿单元，水深小于0.005 m的单元不参加计算，水深介于两者之间的单元为半湿润单元。河道糙率在数值模拟中具有十分重要的作用，本模型根据实测水流资料率定、调试模型糙率，最终确定模型计算河段的糙率取值区间在0.028～0.035之间，模型中涡粘系数取值0.28 m2/s，时间步长取为0.01～30 s。

3.3 模型验证

为了使模型验证更加准确，分别采用2007年8月14—15日大潮及8月7—8日小潮两次水文测验资料进行验证计算，计算时下游出口边界由三江口实测潮位过程控制，河道内共有洋埕闸、宁海桥下和三江口3个水文测量断面。

大潮以及小潮时，沿程三江口测点、宁海桥下测点以及洋埕闸测点潮位、流速过程计算值与实测值的对比见图2～图5所示。

图2 大潮潮位计算值与实测值对比

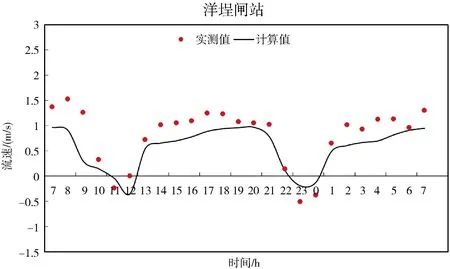
图3 大潮流速计算值与实测值对比

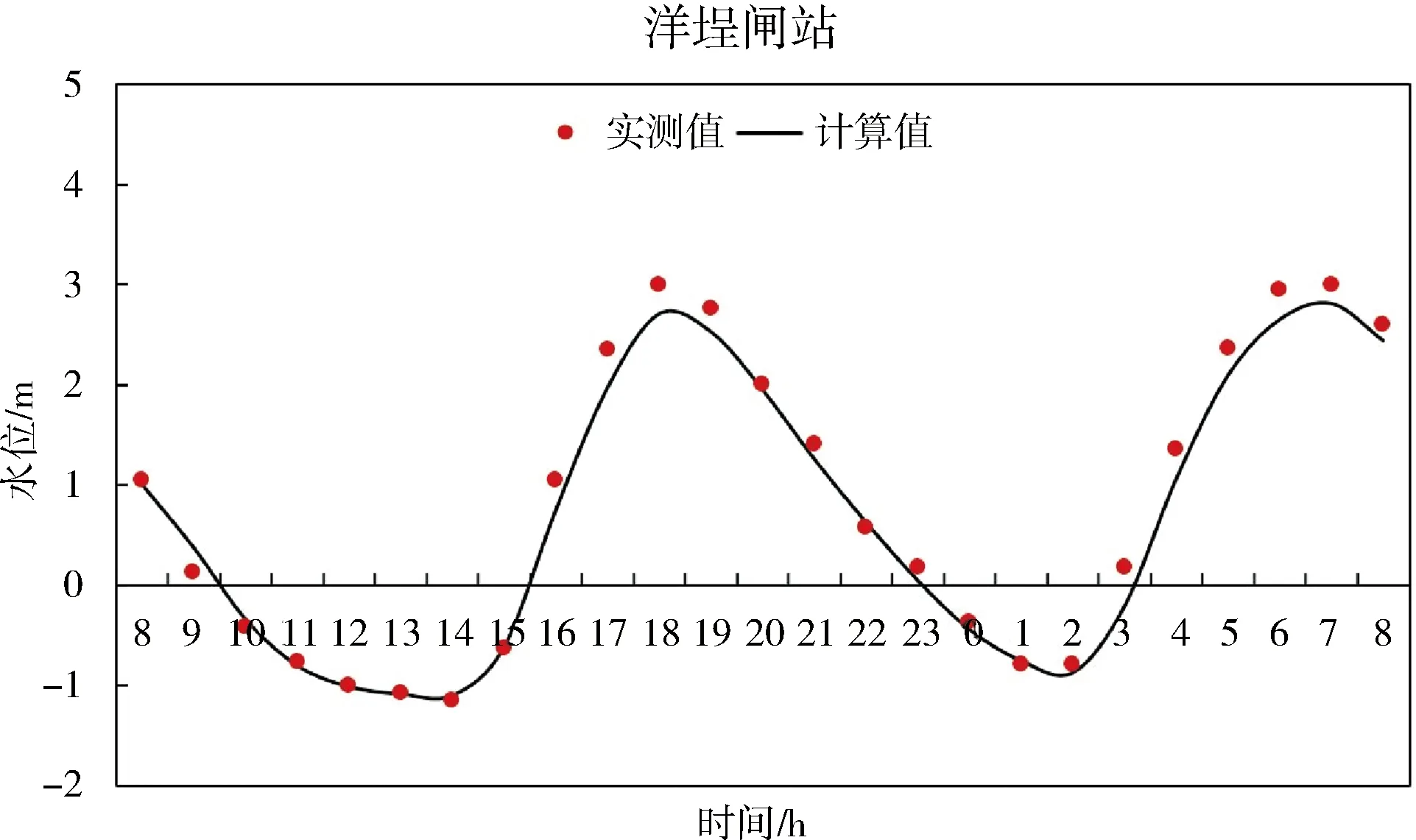
图4 小潮潮位计算值与实测值对比

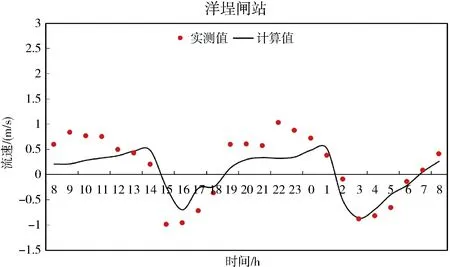
图5 小潮流速计算值与实测值对比

由验证结果可知，3个测点的潮位与流速计算值与实测值吻合性较好，符合相关规程的要求，比较准确地反映了木兰溪下游河道的水流运动规律，因此认为模型参数的选取是合理的，可以将此模型用于计算分析木兰溪宁海闸闸闸下水位流量关系。

4 宁海闸水位流量关系数值计算

木兰溪位于福建省东部沿海莆田市境内，下游为滨海南北洋平原(又称兴化平原)，木兰溪流域面积为 1 732 km2，河长为105 km，系闽中最大河流，木兰陂以下34.1 km河道为木兰溪下游感潮河段，潮流作用明显。拟建宁海闸水利工程处于木兰溪下游河口段，距离宁海桥下约800 m(木兰溪流域水系和拟建闸位置如图6所示)。水闸枢纽工程由闸室、门库、弧门支座、消能工、上下游接线护岸、控制房、管理房等建筑物组成，宁海闸闸室由河中央常规闸加两侧平面立轴式弧形钢闸门组成，其中立轴式弧门共布置2孔，单孔净宽为90.0 m，闸室底板顶高程为-0.50 m。其中常规闸共布置3孔，单孔净宽为25.0 m，闸室底板顶高程为-2.50 m。宁海闸设计洪水标准为100年一遇(P=1%)，校核洪水标准为300年一遇(P=0.33%)，设计防潮标准为50年一遇高潮位(P=2%)。闸上正常蓄水位为2.80～4.30 m，主汛期闸上的限制蓄水位为2.80 m。

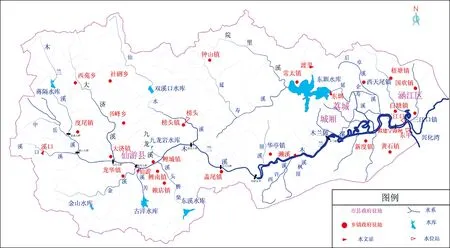
图6 木兰溪流域水系及拟建宁海闸位置示意

4.1 计算条件

本次宁海闸闸下水位流量关系数值模拟计算中，考虑水闸泄流分别遭遇低潮和高潮，通过利用MIKE21水动力模型仿真计算闸下水位流量关系，主要用于宁海闸闸下消能防冲的设计以及复核宁海闸的泄流能力。模型上边界为水闸各级下泄流量，下边界条件基于多年平均潮位过程进行数值模拟计算。

4.2 闸下潮位合理性分析

拟建宁海闸位于验证点宁海桥下游侧，通过验证结果可知实测值与计算值吻合良好(见图2)，另外计算现状条件下外海边界为多年平均潮位过程时，东甲潮位站潮位过程线，并与东甲站实际潮位过程线对比(如图7所示)，结果显示计算结果良好，所以，利用数值模拟计算得到闸下的多年平均潮位过程线是可行的(见图8)。由过程线可知，河道整体潮位分布形态正常，计算涨潮时东甲最高潮位为5.04 m，闸下最高潮位为5.03 m，仿真计算成果合理。

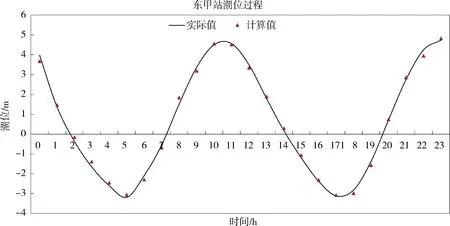
图7 现状条件下东甲站实际潮位与计算潮位过程

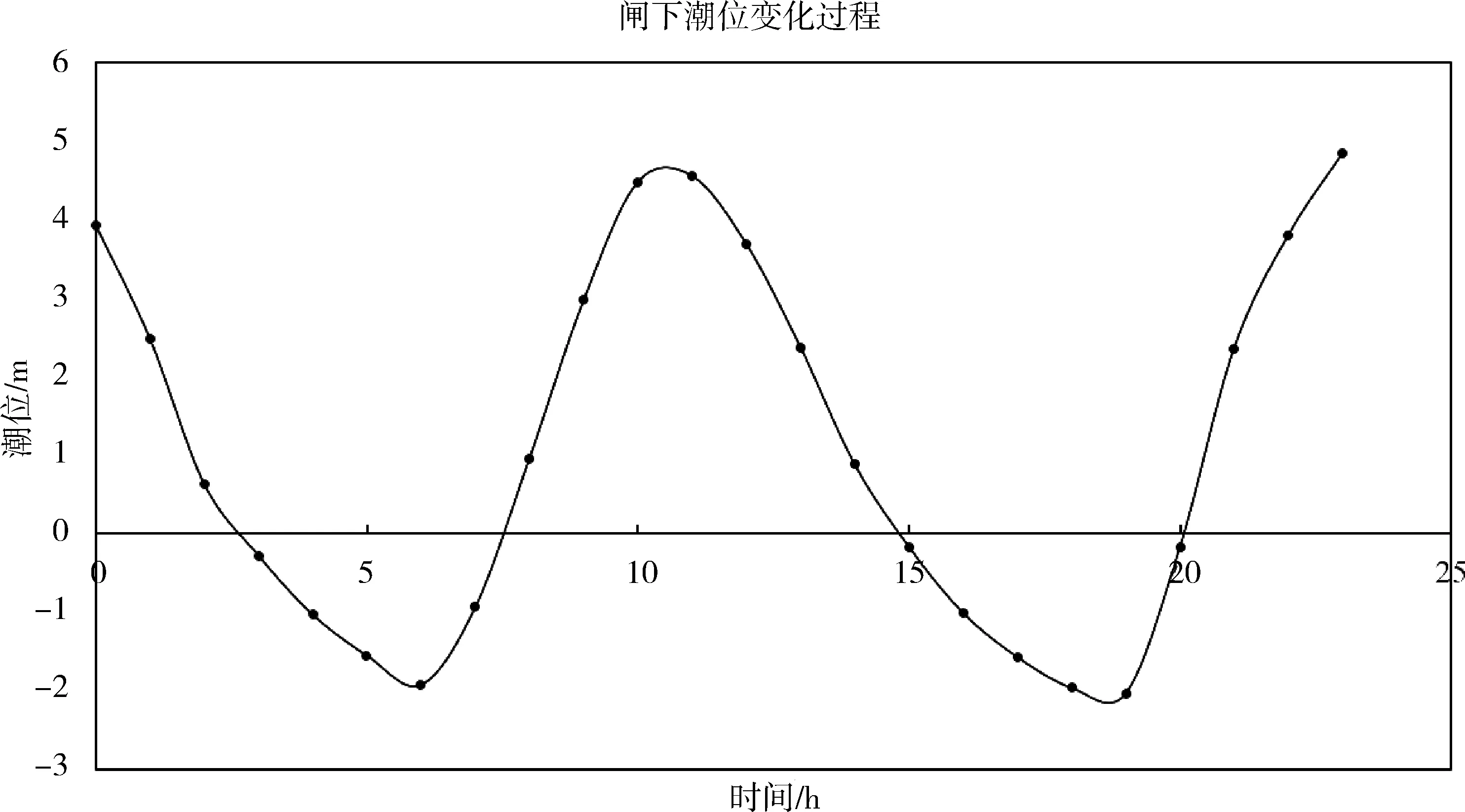
图8 现状条件下闸下多年平均潮位过程

4.3 闸下水位流量关系计算成果

本次利用二维水动力数学模型仿真计算水闸下泄各级流量分别与闸下低潮位、高潮位遭遇情况时宁海闸闸下水位流量关系，具体情况如下。

1) 泄流量遇低潮工况

利用MIKE21水动力模型仿真计算宁海闸下泄各级流量分别与低潮位遭遇工况下的闸下水位流量关系，并统计计算结果(见图9、表1)。

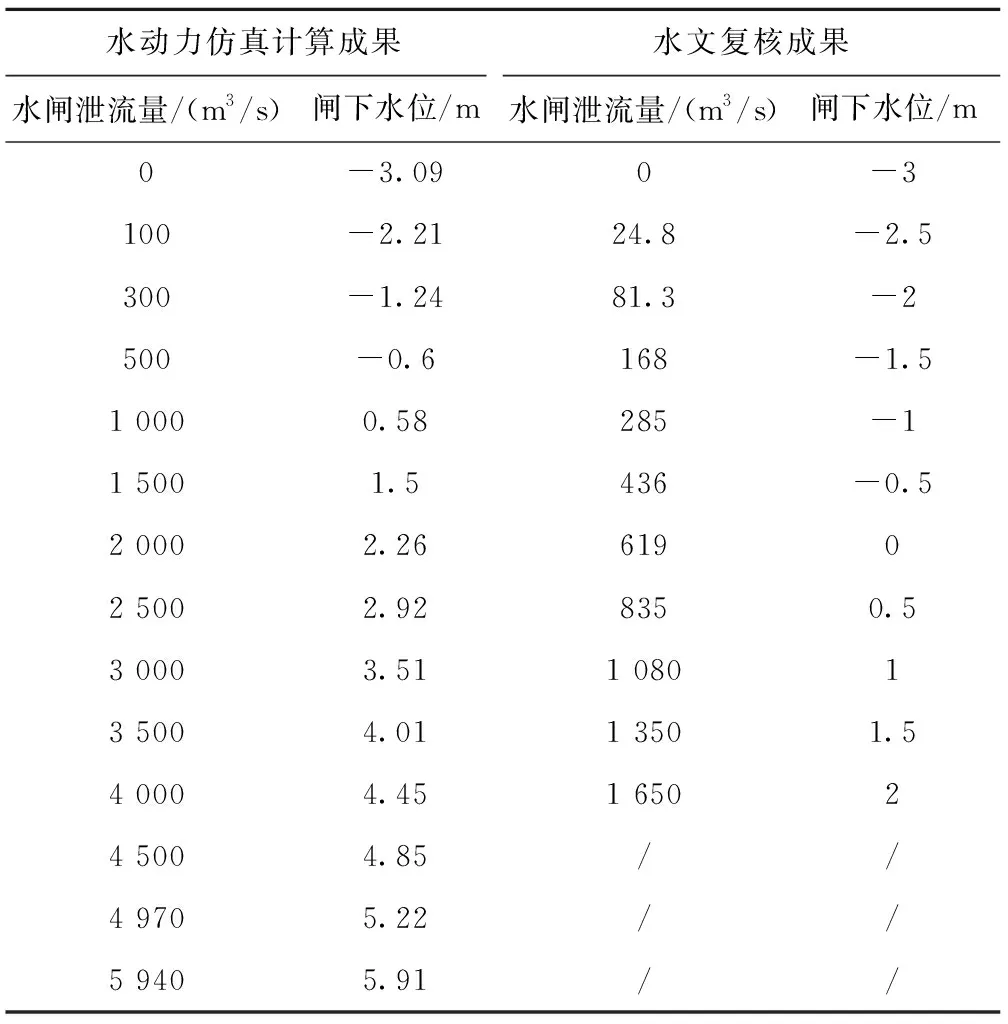
表1 宁海闸泄流量遇低潮工况时，闸下水位流量关系比较

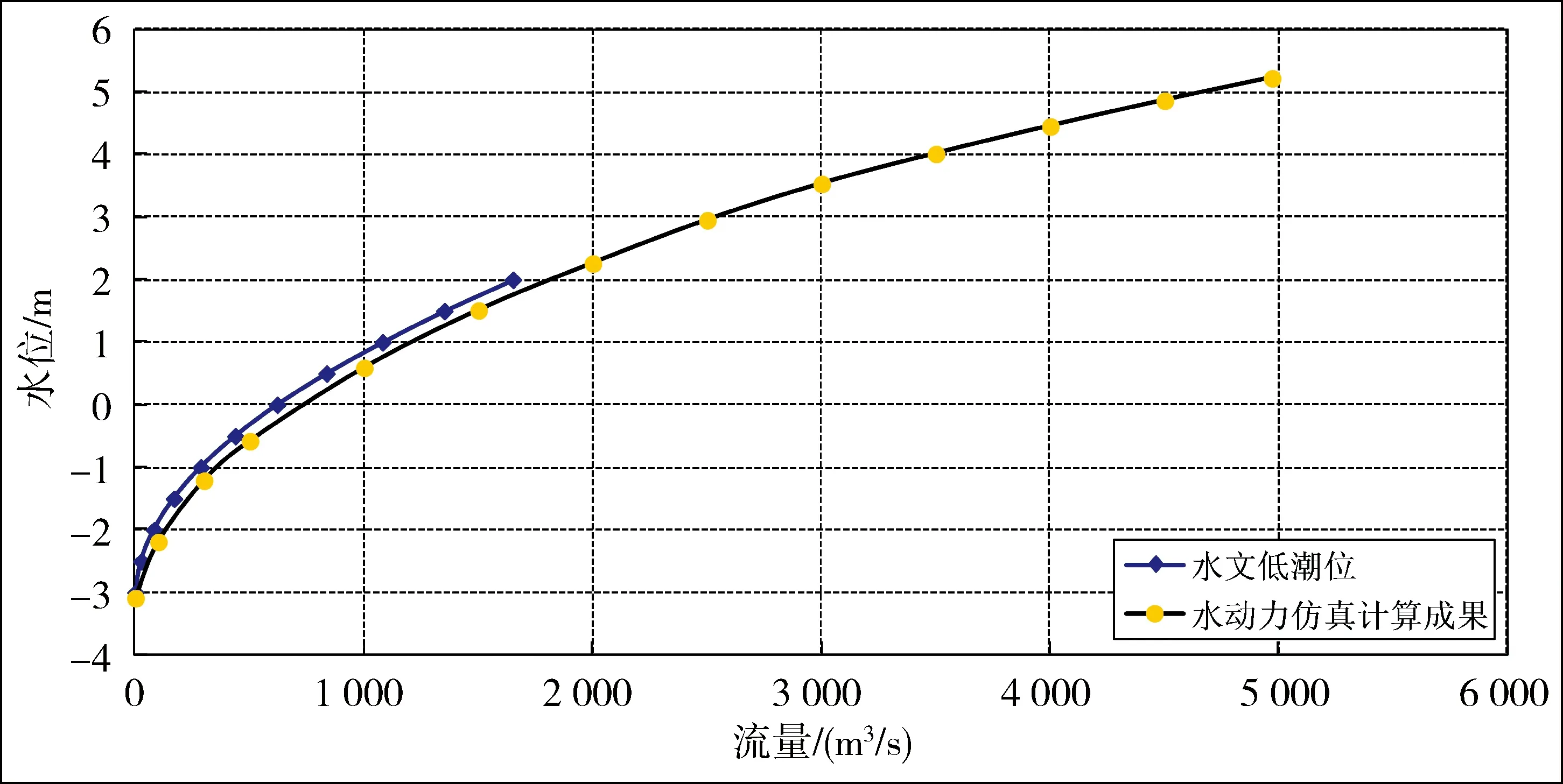
图9 宁海闸泄流量遭遇低潮时的水位流量关系

通过对比分析本次仿真计算成果与水文复核计算成果，可以看出，在相同流量下，水动力仿真计算得到的水位值稍低，两种方法计算得到水位流量关系整体趋势一致，可据此进行水闸消能防冲设计。

2) 泄流量遇高潮工况

利用MIKE21水动力数学模型计算水闸下泄各级流量分别匹配闸下多年平均潮位过程，计算得到宁海闸闸下水位流量关系。由于水文计算成果是考虑下游水位为平均高潮位2.19 m，故本次数模计算提取相同条件下的闸下水位与之对比。结果显示，在流量较小时，相同流量情况下，水文公式计算得到的水位值略小，随着水闸下泄流量的增加，相同流量下，水文公式计算的水位略高，两者结果相差较小，趋势较为一致，说明水动力仿真计算能够较准确的模拟下游潮位与径流共同作用下闸下水位流量关系，因此，对于洪水工况的水闸泄流能力问题，可依据水动力数模仿真计算成果进行复核(如图10、表2)。

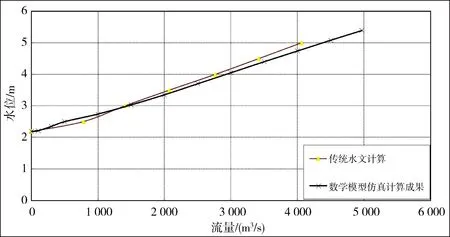
图10 宁海闸泄流量遭遇高潮时的水位流量关系

表2 宁海闸泄流遇高潮工况时，闸下水位流量关系

5 结语

通过实测地形、水文资料建立MIKE21水动力数学模型，在验证合理的基础上，利用该模型仿真计算宁海闸下泄不同量级流量分别遭遇低潮、高潮的工况，得到闸下水位流量关系。结果表明利用水动力数学模型仿真计算方法能够较准确的得到径流和潮流共同作用下感潮河段闸下水位流量关系，该方法相对传统水位流量关系计算方法更加仿真、准确，并且简明、直观、适应多种较复杂条件，计算结果可用于水闸消能防冲设计和复核水闸泄流能力。对于受潮流作用明显的闸下水位流量关系计算具有一定的参考价值，并且该模型建立后也可以进行河道水面线以及防洪影响分析计算等。