基于培养学生科学思维能力的高中物理教学设计——以“向心力”为例

吴梦雷

（江苏省扬州中学，江苏 扬州 225009）

学科核心素养是本轮课程改革的核心与关键，通过最近数年的研讨，教育界已基本达成共识，即学科育人的价值主要体现在培养学生正确的价值观念、必备品格和关键能力.具体到物理学科，核心素养主要包括“物理观念”“科学思维”“科学探究”“科学态度与责任”四个方面.这四个方面的能力是满足学生终生发展需要，以适应当下和未来社会发展挑战的重要保障.本文选择“科学思维”这个方面进行探讨.相较于“思考”，“思维”是一个上位概念，是指利用表象概念进行分析、综合、推理等认识活动的过程，“科学思维”则是指基于事实和证据，本着严谨务实的态度，运用归纳概括、演绎推理、模型建构、批判思维和创造思维等方法认识世界，解决物理问题的思维习惯与能力.培养学生的科学思维能力是物理课堂教学设计的核心目标，无论是情境的创设、实验的展示，还是探究的构思，都离不开提升学生科学思维能力这根主轴.向心力是促使物体做圆周运动的关键原因，其方向为什么指向圆心？大小与哪些变量有关？满足什么定量关系？这些问题都是提升学生科学思维能力的良好素材，教师在设计时通过情境转换、科学推理与论证、质疑创新等方法，可帮助学生深刻领悟自然现象背后的物理规律.

1 基于培养学生科学思维的教材分析

在2004版人教版教材中，向心力这一节内容置于向心加速度之后.学生在教师的引导下，运用极限思想，从理论上推导出向心加速度的方向、表达式之后，再结合牛顿第二定律，很快就能得出向心力的方向和表达式，最后通过圆锥摆粗略验证向心力的公式，逻辑性很强.而在2019版人教版教材中，却将向心力这一节内容调整到了向心加速度之前，让学生先通过定性实验感受向心力的方向和大小，再通过手摇式向心力演示器探究向心力与角速度、质量、半径之间的定量关系，归纳得出向心力的表达式，紧接着通过牛顿第二定律推导出向心加速度的表达式，最后再利用极限思想从理论上进行验证.

新一版的教材为什么做出如此调整？笔者觉得编者的用意可能有三个：一是与向心力相比，向心加速度的概念更为抽象，不利于学生在学习过程中调动生活经验；二是为了突出物理实验在培养学生科学探究能力和科学态度方面的重要作用；三是为了响应新课标将“探究向心力大小与角速度、质量、半径的关系”确定为学生必做实验的要求.

在新的知识框架下，学生通过上一节内容的学习，已经知道了圆周运动的概念，学会了从运动学的角度描述圆周运动的快慢，并掌握了相关物理量之间的定量关系.本节内容的任务是从动力学的角度，探究圆周运动中向心力与其它运动学参量之间的关系，归纳得到匀速圆周运动中向心力的方向、大小的计算公式.最后，针对生活中更为常见的变速圆周运动、一般曲线运动，教材简单介绍了研究的方法，由特殊到一般，循序渐进，符合学生认知规律和学科特点.

2 以科学思维为先导的教学过程设计

2.1 复习引入，理解描述圆周运动快慢的相关物理量的本质属性、内在规律及相互关系

问题1.为了描述质点做圆周运动的快慢，我们引入了哪些物理量？它们之间满足怎样的数学关系？

生：线速度v，角速度ω，周期T，频率f，还有转速n.如图1所示.

图1 物理量之间的关系

问题2.如果质点的线速度v大小不变，我们通常将这种运动称为“匀速圆周运动”.匀速圆周运动是匀速运动吗？

生：不是匀速运动.因为线速度v的方向一直在变化，所以匀速圆周运动是变速运动.

设计思路：复习的虽是“旧知识”，但只要有“新视角”，特别是有那些看似矛盾的叙述，可很快激起学生挑战的欲望，加深思维的深刻性.与此同时，若学生基于科学思维领悟了所学内容在整个知识架构中的位置及其关联，由此产生的“掌控感”将非常有利于培养学生学习的内在动力，因此复习引入时最好采用单元整体备课的视角.

2.2 构建模型，科学推理匀速圆周运动中物体所受向心力的方向

问题1.如图2所示，在松木板上用图钉固定细线的一端，另一端系个钢球.给钢球一个初速度，使其做圆周运动，为什么小球会慢慢停下来？在什么情形下，小球的转动可视为匀速圆周运动？

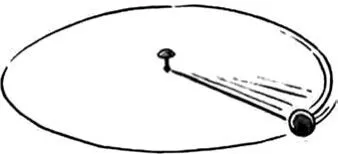
图2 钢球在细线牵引下绕图钉做圆周运动

生：小球慢慢停下来主要是因为受到了松木板的摩擦力.如果小球受到的摩擦力与重力、支持力、拉力相比非常小，可以被忽略，线速度v减小得非常缓慢，则小球的转动可视为匀速圆周运动.

问题2.做匀速圆周运动的小球受哪些力？合力指向哪里？

生：小球受重力、支持力还有细线拉力的作用.重力和支持力抵消，因此拉力就是小球受到的合力，沿半径指向圆心（图3）.

图3 小球的受力示意图

问题3.如图4（a）人们在游乐场中乘坐旋转飞椅时所做的运动，可等效成用细线悬挂的小球在水平面内做的匀速圆周运动（圆锥摆）.小球受哪些力？合力指向哪里？

图4 旋转飞椅和圆锥摆

生：小球受重力，还有细线拉力的作用.合力沿轨迹圆的半径指向圆心.

师：合力有没有可能不在水平面内，指向左下方？

生：不可能.因为小球运动状态的变化仅发生在水平面内，竖直方向是平衡的，所以合力一定处于水平面内（图4（b））.

师：在水平面内，难道就一定指向圆心吗？（学生一时语塞）下面我们利用极限思想从理论上进行论证.如图5所示，若小球自A点出发，沿逆时针方向做匀速圆周运动，经过极短的一段时间 Δt，抵达B点.将vA的首端平移到B点，连接vA、vB的末端，并指向vB，得到Δv，三者正好构成一个等腰三角形，其顶角Δθ与半径转过的角度相等，均非常小，因此该等腰三角形的底角趋向于90°，在极限情况下，可认为Δv⊥vA.将Δv的首端向下平移到A点，发现其恰好沿半径指向圆心，而Δv的方向也是加速度a的方向.根据牛顿第二定律，加速度a的方向也是合外力的方向.因此，我们就从理论上证明了做匀速圆周运动的物体，其受到合外力指向圆心，我们通常称之为向心力.

图5 小球从A运动到B的速度变化量

问题4.如图6，月球环绕地球做匀速圆周运动，向心力由什么力提供？粗糙转盘上的物块随转盘一起绕转轴做匀速圆周运动，无相对滑动，向心力由什么力提供？结合这些实例，思考向心力是一种新的性质的力吗？

图6 圆周运动的两个实例

生：地球施加的万有引力，圆盘施加的静摩擦力.向心力可有由引力、弹力、摩擦力等外力提供，也可以有若干个外力的合力提供，是一种按作用效果命名的力，并不是一种新的性质的力.

设计思路：不少学生觉得教材中的表述“大量实例都表明，做匀速圆周运动的物体所受的合力总指向圆心”含糊其辞，说服力不强.为此，笔者引导学生基于生活中的圆周运动建构出匀速圆周运动的模型，以科学思维为先导，采用严密的理论推导得出向心力的方向，进而回到生活中的圆周运动进行校验，教学流程更为流畅，更符合学生的认知预期.

2.3 实验探究，科学论证向心力与其它变量之间的定量关系

探究活动1.感受匀速圆周运动中的向心力.

问题1.如图7所示，在圆锥摆中，向心力Fn与细线拉力T、圆锥半顶角θ之间满足什么数学关系？

图7 不同半顶角情况下的受力示意图

生：Fn=Tsinθ.

师：如果小球的转速大一些，半顶角也会大一些.当θ→90°时，sinθ→1，此时Fn≈T，所以我们可以通过细线上拉力的大小来感知向心力的大小.请大家转动两个质量不同的糖果（图8），感受向心力Fn与角速度ω、半径r、质量m之间的定性关系？

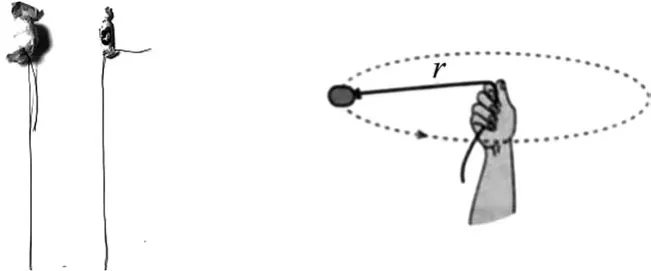
图8 旋转质量不同的糖果

学生体验后，汇报实验结果：（1）角速度ω越大，向心力Fn越大；（2）半径r越大，向心力越大；（3）质量m越大，向心力越大.

问题2.向心力Fn同时与多个变量有关，应采取哪种实验方向进行研究？

生：控制变量法.

问题3.当角速度ω、质量m、半径r增大时，向心力Fn都会随之增大.向心力Fn与这3个变量之间可能满足什么数学关系？

生：可能满足正比关系，也可能与变量的2次方、3次方，或者平方根满足正比关系.

探究活动2.利用向心力演示器探究Fn与角速度ω、半径r、质量m之间的数学关系.

问题1.如图9，分别将皮带置于塔轮上、中、下3层，观察左、右塔轮的转速之比？

图9 向心力演示器及塔轮示意图

生：当皮带置于最上层时，左侧塔轮转1圈，右侧塔轮也转1圈；置于中间那层时，左侧塔轮转1圈，右侧塔轮转2圈；置于最下面那层时，左侧塔轮转1圈，右侧塔轮转3圈.

问题2.因为ω∝n，所以在转速之比已知的情况下，角速度ω之比也是明确的.请同学们确保左右两侧旋臂上小球的质量m、转动半径r相等，在上述3种情况下，记录左右两侧套筒上漏出的标尺格数之比（向心力Fn之比）填入表1.

表1 探究向心力与角速度之间的关系

问题3.向心力Fn和角速度ω之间显然不是正比关系，猜一猜向心力Fn和什么成正比？

生：向心力Fn和向心加速度ω的平方存在正比关系（见表2）.

表2 探究向心力与角速度平方之间的关系

问题4.我们已经知道了Fn∝ω2，那如何利用向心力演示仪探究向心力Fn与质量m、半径r之间的关系呢？

生：（1）将皮带置于最上层，确保角速度ω相等，以及转动半径r相等，左右两侧放置质量之比为1∶2的铝球和钢球（表3），探究Fn与质量m之间的关系；（2）将皮带置于最上层，确保角速度ω相等，使用两个质量均为m的钢球，令左右两侧钢球转动的半径之比为1∶2，探究Fn与半径r之间的关系.如表4.

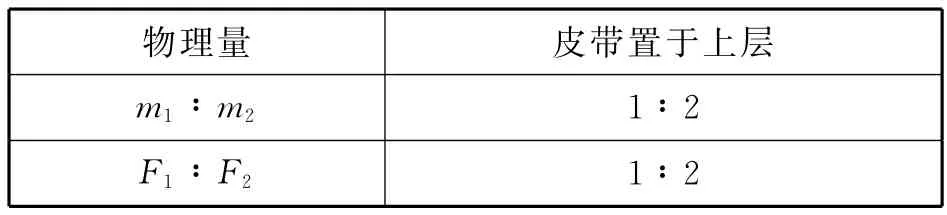
表3 探究向心力与质量之间的关系

表4 探究向心力与半径之间的关系

师：利用向心力演示仪，我们探究发现F∝m、F∝ω2、F∝r，合起来就是F∝m ω2r，若采用国际单位制，则有F=mω2r.上述探究过程看似严谨，实则存在一个硬伤，即支撑结论的数据太少，说服力不够.下面我们用更精确的DIS实验进行研究.

探究活动3.用朗威.无线向心力演示器（图10）研究向心力Fn与角速度ω、半径r、质量m之间的数学关系.

图10 无线向心力演示器

实验演示步骤1：探究向心力Fn与角速度ω之间的关系（使用质量为0.024kg的砝码在转动半径为0.10m的情况下进行实验）.

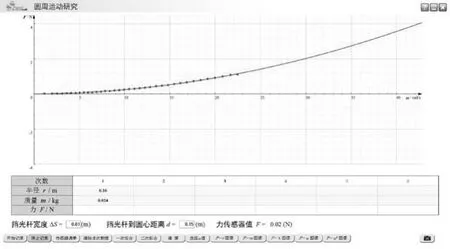
图11 向心力与角速度之间的函数关系

结论1：质量m、半径r一定时，向心力Fn的大小与ω2成正比（见图12）.

图12 向心力与角速度平方之间的函数关系

实验演示步骤2：探究向心力Fn与质量m之间的关系.使用质量分别为0.012kg、0.024kg、0.036kg的砝码进行实验，如图13所示.

图13 不同质量对应向心力的实验结果

结论2：角速度ω、半径r一定时，向心力Fn的大小与质量m成正比，如图14.

图14 向心力与质量之间的函数关系

实验演示步骤3：探究向心力Fn与半径r之间的关系，使用0.024kg的砝码，在转动半径分别为0.10m、0.09m、0.08m、0.07m的情况下进行实验，结果如图15所示.

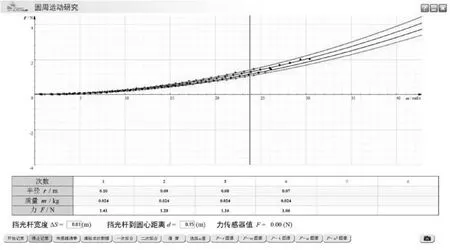
图15 不同半径对应向心力的实验结果

结论3：角速度ω、质量m一定时，向心力Fn的大小与半径r成正比.如图16所示.

图16 向心力与半径之间的函数关系

设计思路：知识的建构不是一蹴而就的，必须经过多次循环，才能实现最终的同化或者顺应.向心力大小的定量公式，笔者在实验的基础上，基于科学思维，设计了定性实验→半定量探究实验→DIS定量探究实验，学生逐步印证自己的猜想，既加深了对物理规律的认知，又提升了科学思维的能力.

3 培养学生科学思维的教学反思

科学思维是人类认识客观世界的方法论，其包含的模型建构、科学推理、科学论证、质疑创新这四个要素，类似一辆汽车的四个轮子，共同驱动人类的观念不断接近宇宙万物的本质属性、运行规律和内在关联.在高中物理课堂上，提升学生的科学思维能力是教学的核心目标之一，笔者在设计本节课的时候，在多个地方刻意进行了强化.

3.1 理想的匀速圆周运动哪里来？——突出模型建构

物理建模就是依据已有经验材料，对一类问题构建问题背景图景，并用物理模型解释和预测现象的科学思维能力的科学实践活动.[1]在授课伊始，笔者引用的两个例子都是生活中的圆周运动，物体会越转越慢，最终停止运动.怎样得到理想的匀速圆周运动呢？学生们很容易从质点模型建构的经验中得到启发，运用理想化的方法，忽略阻力对圆周运动的影响，将物体抽象为质点，即可构建出理想的匀速圆周运动模型.除了理想化方法，我们还可以采用类比联想、等效替代、假设验证等方法构建物理模型，让学生在建模的过程中感悟上述思维方法，辨析相关模型的使用前提，最终能够通过建模来解决实际问题.

3.2 旋转糖果时，为什么细线的拉力可以视为向心力？——突出科学推理

科学推理是基于经验事实建构物理概念，形成物理规律的过程，是发展科学思维的重要途径.教材中设计的感性体验方案，对于为什么能够用细线上的拉力代替向心力，没有详细说明，笔者从一般情形出发，利用极限思想，给予了合理证明，学生深以为然.课堂处处皆学问，细节之处见真章，对于教材上那些受篇幅所限，不能展开论述，而又非常重要的思维节点，我们一定要在教学设计时多下功夫，打通思维脉络，让学生融会贯通.

3.3 向心力与其相关变量之间都满足正比关系吗？——突出科学论证

科学论证是指分析综合、推理论证等方法在科学领域的具体运用.希门尼斯曾指出：科学探究作为一种为了理解自然世界而生产、辩护知识和信念的行动，论证尤其发挥着重要的作用.[2]学生常常可以在一定的事实基础上提出某些定性的观点，但是对于体系严谨，论证严密的物理学来说，那些带有体验色彩的模糊结论显然是难以服众的，必须在可重复实验的事实证据与结论之间形成逻辑关系清晰的思维链条，也就是整合学科知识（包括事实性知识、概念性知识和元认知知识[3]）、联结事实证据、观点，经过多层次递进推理，使之逐步走向定量和精确.本节课在探究向心力大小的决定因素时，笔者让学生经历了“定性→半定量→定量”的过程，边探究边论证，使其充分体悟科学思维的精妙与犀利.

3.4 匀速圆周运动的合外力一定指向圆心吗？——质疑创新

质疑创新是指基于事实证据和科学推理对不同观点和结论提出质疑和批判，进行检验和修正，进而提出创造性见解的能力与品格.在通过实例总结匀速圆周运动中合外力的方向时，学生们普遍认为沿半径指向圆心，此时笔者提出了两个质疑：（1）有没有可能不在轨迹圆平面内，指向左下方？（2）有没有可能在轨迹圆平面内，但不指向圆心？一下子就加大了学生思维的深度，促使学生养成更为严谨的思维习惯，不盲从，学会批判性思维.

4 结语

科学思维能力的培养可以渗透于教学的每一个环节之中.教师在教学设计时，可以通过巧妙创设物理情境，精准设置核心问题，培养学生依据事实、科学建模的学科素养；也可以通过巧妙设置递进问题，培养学生科学推理、科学论证的学科能力；还可以通过扩展设置发散性问题，培养学生质疑创新的学科精神.