阻尼环车轮对钢轨波磨的影响*

杨普淼 张银仙 许 岩 杨布雷 陈光雄

(西南交通大学摩擦学研究所 四川成都 610036)

我国地铁行业飞速发展，极大地提高了城市交通运输效率，但随之而来的钢轨波浪形磨损(波磨)现象困扰了研究人员多年[1]。列车通过有波磨钢轨路段时，轮对垂向力急剧变化，发生强烈的振动和噪声，影响车辆旅客乘坐的舒适度和车辆平稳性能，严重时导致脱轨等恶性交通事故发生[2]。波磨极大地影响了列车安全性能，国内外研究人员提出了许多抑制波磨的措施。GRASSIE[3]将波磨分类为P2共振波磨、车辙波磨、其他P2共振波磨、重载波磨、轻轨波磨和特定轨道结构波磨，并提出了不同解决办法。OOSTERMEIJER[4]指出改变钢轨材料属性能抑制波磨产生。VADILLO等[5]研究指出加设轨枕能抑制短波波磨产生。QIAN等[6]研究证实敷设钢轨阻尼减振器能有效抑制钢轨波磨的产生。崔晓璐等[7]研究了改变轮轨系统结构参数对波磨的影响，并提出最优结构参数。近年来，陈光雄教授提出了轮轨系统摩擦自激振动引起钢轨波磨的理论，并已得到国内外研究人员的认同[7-12]。

随着我国材料行业的飞速发展，材料性能得到了很大的提高。阻尼材料因其特殊减振性能[13]而逐渐被轨道交通研究人员使用。阻尼车轮应运而生，如，扣件阻尼垫、阻尼环[14]、车轮辐板阻尼涂层[15-16]等。其中，因为阻尼环安装简便(能直接镶嵌在轮辋上)，对车轮结构改动小而受到研究者和施工人员的青睐。日本车轮公司设计了橡胶包夹钢材质阻尼环，已用于实际生产。但关于阻尼环对钢轨波磨的影响研究还很少见到报道。

本文作者基于陈光雄教授[6]提出的摩擦自激振动理论，建立了牵引轮对-钢轨-轨枕组成的有限元模型[17]，模拟车辆稳态通过小半径(R≤350 m)曲线轨道工况，采用ABAQUS经典有限元复特征值算法进行了计算预测。文中首先通过与实测数据对比，验证了无阻尼环轮轨模型的正确性；然后在该模型车轮轮毂处添加阻尼环，对比研究有无阻尼环、阻尼环阻尼系数(β)、阻尼环安装位置以及单侧阻尼环宽度对钢轨波磨的影响。

1 模型的建立

1.1 轮轨模型

设定车辆稳态通过曲线半径小于350 m轨道，并以此建立牵引轮对-钢轨-轨枕三维有限元模型，进行仿真计算。车轮选用LM踏面，车轮直径840 mm；钢轨总长36 m；扣件间距625 mm，扣件类型选用DTVI2。车辆通过小半径曲线时，左右轮轨接触位置和接触角差异较大，高轨接触角约32°，低轨接触角约2.1°，如图1所示。

图1中，δR、δL分别为低轨和高轨轮轨接触角；FSVL、FSVR为轮对垂向悬挂力；FSLL、FSLR为轮对横向悬挂力；KRV、KRL、KSV、KSL分别为扣件垂向和横向刚度、轨枕垂向和横向刚度；CRV、CRL、CSV、CSL分别为扣件垂向和横向阻尼、轨枕垂向和横向阻尼。其中，KRV=8.79 MN/m，KRL=40.73 MN/m，KSV=340.136 MN/m，CRV=6 361.29 N·s/m，CRL=1 927.96 N·s/m，CSV=CSL=0.027 54 N·s/m，有限元模型如图2所示。

图1 轮轨接触位置、接触角和蠕滑力方向Fig 1 Wheel-track contact position,contact angle and creep force direction

图2 有限元模型Fig 2 Finite element model

为讨论阻尼环安装位置对波磨的影响，将阻尼环分别安装在外侧、轴侧和双侧(外侧和轴侧同时安装)，如图3所示。实际安装时阻尼环是镶嵌在轮辋中，文中为研究方便，进行了适当简化，将阻尼环贴放在轮辋边缘。

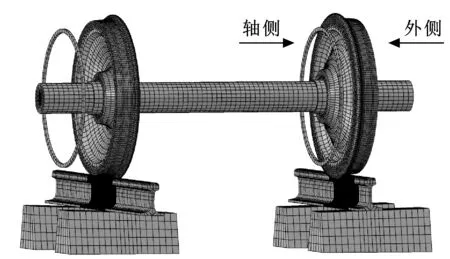
图3 阻尼环模型Fig 3 Damping ring model

1.2 复特征值理论分析

有限元分析中，复特征值法能预测系统发生摩擦自激振动频率和模态，故文中采用该方法预测不稳定振动趋势。假设两接触面(主面、从面)部分网格节点重合，在考虑摩擦力的前提下，对重合节点进行力学平衡计算，得到如下表达式：

(1)

式中：∂表示位移；M表示质量矩阵；C表示阻尼矩阵；K表示刚度矩阵。

忽略摩擦力时，质量、阻尼、刚度矩阵都是严格对阵矩阵。加入摩擦力后，质量、阻尼、刚度矩阵都将变为非对称矩阵。对公式(1)进行特征方程改写，得到以下公式：

(M(γn)2+C(γn)+K)σn=0

(2)

其中，γn是公式(2)求解的特征值，σn是公式(2)特征值对应的特征向量。σn可记作：

σn=αn+jβn

(3)

式中：αn是特征向量的实部，βn是特征向量的虚部，j为虚数。

对该特征向量进行多次迭代计算，得到第i阶模态。所以，当特征向量实部为正时，计算得到模态不收敛，即系统容易发生不稳定振动。但是一些实部为正，绝对值很小的特征向量，也不能引起系统不稳定振动。为了更准确地评定系统状态，引入等效阻尼比来表示系统是否存在不稳定振动，其计算公式为

ζ=-2αn/(|βn|)

(4)

式中：ζ是等效阻尼比。

当ζ为负时，系统发生不稳定振动，且绝对值越大，发生不稳定振动的趋势越强，文中使用该指标来判断系统是否有发生摩擦自激振动趋势。

2 计算结果及分析

2.1 有无添加阻尼环模型分析

根据陈光雄教授提出的摩擦自激振动理论，当车辆通过小半径(R≤350 m)曲线，导向轮对中内轮蠕滑力饱和，容易引起摩擦自激振动。有限元模型模拟车辆通过小半径曲线的计算结果如图4所示。无阻尼环中，等效阻尼比ζ最小为-0.023 78，对应频率为502.32 Hz。线路实测波磨频率为200～1 000 Hz[18]，地铁通过小半径曲线时速约55 km/h。根据速度、波长和频率关系[19]，得到波长约为30.4 mm，符合线路实测数据。该频率对应的模态如图5所示，外轨几乎没有变形，内轨发生严重变形。这表明当系统发生摩擦自激振动时，内轨产生波磨而外轨不会产生波磨，这点与线路实况高度吻合，所以文中模型能用于预测波磨计算。

图5 频率f=502.32 Hz时无阻尼环轮对的模态(ζ=0.023 78)Fig 5 Mode of the wheelset without damped ring at frequency of 502.32 Hz(ζ=0.023 78)

文中所有阻尼环材料参数采用ABAQUS中的瑞利阻尼[20]，α=0、β=1×10-5。后文所有计算材料参数，如未特殊说明，都取该数值。由图4可以看出，当车轮外侧添加阻尼环以后，得到阻尼比ζ=-0.021 22，f=512.99 Hz。最小等效阻尼比对应的频率差异不大，绝对值有一定的减少，根据公式(4)可得，绝对值越小，系统发生不稳定振动的趋势越小，从该对照组可以得出轮对添加阻尼环能一定程度上抑制轮轨系统波磨产生。这是因为，波磨是一种轮轨低频不稳定振动现象，当轮轨接触部位产生不稳定振动时，由于轮辋材质较硬，阻尼环硬度低，阻尼环将会发生变形；阻尼材料两边所受合应力相互抵消，故能起到减振吸振效果，能吸收一部分不稳定振动源的能量，即抑制波磨产生。

图4 有、无阻尼环轮对时频率-等效阻尼比关系Fig 4 Relationship between frequency and equivalent damping ratio of wheelset with and without damping ring

2.2 外侧阻尼环阻尼系数对钢轨波磨的影响

分别取阻尼系数β为1×10-6、1×10-5、1×10-4和1×10-3，研究轮对外侧阻尼环阻尼系数β对轮轨系统波磨发生趋势的影响，结果如图6所示。4组阻尼系数值对应的模型等效阻尼比都大于无阻尼环模型的等效阻尼比值，这说明添加不同阻尼系数的阻尼环都能降低波磨产生的趋势。当阻尼系数β的数量级为10-6和10-5时，系统都存在2个负等效阻尼比，等效阻尼比系数分别为-0.022 23和-0.021 22，数值差异不大，如图7所示。阻尼系数的量级达到10-4和10-3时，与前两组对比，等效阻尼比增加了9倍左右且只存在一个负等效阻尼比，如图8所示。

图6 等效阻尼比随阻尼系数β的变化Fig 6 Variation of equivalent damping ratio with damping coefficient β

图7 β=1×10-6时频率-等效阻尼比关系Fig 7 Relationship between frequency and equivalent damping ratio at β=1×10-6

图8 β=1×10-4时频率-等效阻尼比关系Fig 8 Relationship between frequency and equivalent damping ratio at β=1×10-4

在β=1×10-3时，模型无负等效阻尼比(此处为方便表示，将该ζ记为0)，表示轮对在通过小半径曲线时，不会产生任意频率的摩擦自激振动，理论上能完全抑制波磨的产生，如图9所示。阻尼系数β代表材料的吸振抗振能力，研究表明随β的数量级提升，阻尼材料的减振性能逐渐升高，吸收不稳定振动能力增强。模型抑制波磨发生的能力逐渐增加。当β数量级为10-4和10-3时，系统稳定性有显著提高。

图9 β=1×10-3时频率-等效阻尼比关系Fig 9 Relationship between frequency and equivalent damping ratio at β=1×10-3

2.3 单侧、双侧添加阻尼环模型稳定性分析

阻尼环安装位置分为外侧、轴侧和双侧，如图3所示。3组模型计算结果如图10所示。

图10 阻尼环不同安装位置的等效阻尼比计算结果Fig 10 Calculation results of equivalent damping ratio at different installation sites

在轴侧添加阻尼环后，进行复特征值计算，得到等效阻尼比ζ=-0.020 68，f=510.12 Hz。相比外侧安装阻尼环计算得到的ζ=-0.021 22，等效阻尼比绝对值在减小，系统发生不稳定振动的可能性有所降低。双侧(外侧和轴侧)添加阻尼环后，计算发现ζ=-0.020 27，f=518.12 Hz，轴侧添加阻尼环，等效阻尼比绝对值又有所减小，系统稳定性更好一些。

可见，外侧、轴侧和双侧添加阻尼环后，利用阻尼材料的减振特性，吸收振源能量，三者在不同程度上才能抑制波磨的产生和发展。3种阻尼环安装位置的等效阻尼比虽呈上升趋势，但等效阻尼比差异在0.001左右，对系统稳定性影响的差异不大。

2.4 单侧不同阻尼环几何尺寸对波磨的影响

设置阻尼环截面为矩形(如图11所示)，且矩形宽度D分别为16 、18.5、21 cm，研究轴侧阻尼环几何尺寸对波磨的影响，计算结果如图12所示。D=16 cm时，ζ=-0.020 46，f=511.46 Hz；D=18.5 cm时，ζ=-0.020 68，f=510.12 Hz；D=21 cm时，ζ=-0.020 53，f=514.83 Hz。可见，三者的等效阻尼次差异在0.000 1量级。据此得到，轴侧不同阻尼环尺寸对轮轨系统稳定性的影响大致相同，但抑制钢轨波磨能力都高于无阻尼环轮轨模型，与2.3节所得结论类似。

图11 阻尼环截面图Fig 11 The cross section of damping ring

图12 轴侧不同宽度阻尼环的等效阻尼比计算结果Fig 12 Calculation results of equivalent damping ratio of damping ring on axis side with different width

设置矩形宽度D分别为17、19.5 和22 cm，研究外侧阻尼环不同宽度对系统稳定性的影响，计算结果如图13所示。矩形宽度为17 cm时，ζ=-0.021 63，f=511.46 Hz；矩形宽度为19.5 cm时，ζ=-0.021 22，f=512.99 Hz；矩形宽度为22 cm时，ζ=-0.021 58，f=511.12 Hz。可见，随阻尼环宽度的增大，ζ绝对值先减小后增大，当D=19.5 cm时，ζ绝对值最小，系统稳定性最高，该宽度为外侧阻尼环的最优尺寸。波磨大多发生小半径曲线内轨，其接触状态如图1所示，轮轨接触位置相对更靠近外侧阻尼环，系统整体稳定性对外侧阻尼环结构变更为敏感，所以外侧阻尼环结构变化更能影响系统稳定性。

图13 外侧不同宽度阻尼环的等效阻尼比计算结果Fig 13 Calculation results of equivalent damping ratio of damping ring on outer side with different width

3 结论

(1)地铁通过小半径曲线(R≤350 m)时，内轨的蠕滑力饱和，有极大的可能性发生摩擦自激振动，即发生波磨。轮对添加阻尼环后，能有效减缓钢轨波磨的发生趋势。

(2)阻尼环车轮抑制波磨产生趋势的能力随着阻尼系数β的增大而增大。β=1×10-3时，阻尼环轮轨模型能完全抑制波磨的产生。

(3)外侧、轴侧和双侧3种安装位置的阻尼环都能有效减缓钢轨波磨的产生，但不同安排位置对钢轨发生趋势的抑制能力差别不大。

(4)安装在轴侧的阻尼环，其宽度变化时抑制车轮波磨的能力没有明显差别。安装在外侧的阻尼环，其宽度增加时，抑制车轮波磨的能力呈先增加后减小的趋势，存在最优的阻尼环宽度(如文中的宽度19.5 mm)，使得阻尼环车轮的波磨抑制能力最佳。