结构参数对压裂双弯头冲蚀及流致变形的影响*

杨思齐 樊建春 张来斌

(中国石油大学(北京)安全与海洋工程学院 北京 102249)

水力压裂是一种广泛应用的油气井开发增产措施，在压裂过程中，高压的压裂液通过地面高压管汇系统运输到井下形成微裂缝，压裂液中所携带的固体颗粒作为支撑剂保持裂缝张开，从而提高油气生产效率[1]。作为关键的压裂设备，高压管汇系统不仅承受极高的内压载荷，还遭受流体中的固体颗粒冲蚀磨损。在整个高压管汇系统中存在大量双弯头元件，高压携砂压裂液在双弯头中多次改变流向,使得双弯头结构极易发生由冲蚀和变形破坏带来的穿孔甚至爆裂等危险事故，对现场作业构成重大威胁[2]。

对于冲蚀磨损问题，许多学者利用试验或数值模拟的方法，在这方面做了大量研究。在冲蚀试验方面，张继信等[3]对30CrMo平板试样进行冲蚀磨损实验，研究了不同冲击速度下材料冲蚀磨损性能。AL-BUKHAITI等[4]开展了泥浆冲蚀试验，研究了不同冲击角度下材料冲蚀磨损变化规律。ARABNEJAD等[5]对不同碳钢材料开展了冲蚀试验研究，分析了材料表面硬度对磨损率的影响。孙秉才等[6]研究了材料应力状态对其抗冲蚀性能的影响。在数值模拟方面，WANG等[7]利用CFD模拟，分别研究了颗粒的粒径及弯头二次流对石油管道冲蚀的影响。陈宇和马贵阳[8]利用DPM模型，对异面三通管在不同流速、不同颗粒直径、不同质量流量下的冲蚀严重度进行了模拟计算。宋晓琴等[9]针对天然气集输管道90°弯头，分别研究了集输压力、重力方向、流速等参数对其冲蚀影响。上述对于冲蚀磨损的相关研究，大多是通过改变流体流动参数进行研究，侧重于结构参数对冲蚀的影响较少。在实际压裂工况下，流体参数的选择往往是由储层地质特征及油气井开发需要决定，难以实现主动修改压裂液流动参数以减缓冲蚀磨损程度，由此从管汇结构参数的角度分析其对冲蚀率的影响从而改善管件冲蚀磨损状态是很有必要的。

随着计算流体力学(CFD)和计算结构动力学(CSD)的发展，CFD-CSD耦合仿真成为了分析管道流固耦合问题有效的分析方法，郭庆[10]利用FSI分析方法，研究了不同管道支撑结构、不同管道长度和不同管内流体流速对流固耦合作用影响。ZHU等[11]针对三通管结构，分别讨论了流速、管径比和分叉角度对管件流场参数、变形及等效应力的影响。然而，很少有学者将冲蚀磨损和结构变形进行综合分析。并且，现有的研究往往只侧重于对单弯头的分析，针对双弯头结构的相关研究较少。因此，本文作者利用ANSYS Workbench多物理仿真平台，对高压管汇双弯头结构在压裂工况下的冲蚀磨损和流致变形进行了综合分析；采用了DPM模型和双向FSI方法，通过一系列数值模拟，分别讨论了双弯头管汇结构参数如连接直管长度、管道内径及弯管间连接角度对其冲蚀率和变形程度的影响。

1 建模及网格划分

文中选用压裂双弯头管汇作为研究对象，进出口直管长度为1 500 mm，弯头内径Di在50～90 mm之间变化，管道壁厚为18 mm保持不变。管道外径为Do=106 mm，连接直管长度Lc在Do～6Do之间变化，连接角度θ分别为0°、90°和180°，弯头曲率半径R保持为2Di。以Di=70 mm，Lc=1.5Do=159 mm，θ=90°的模型作为参照案例，其管壁及管内流场建模如图1所示。

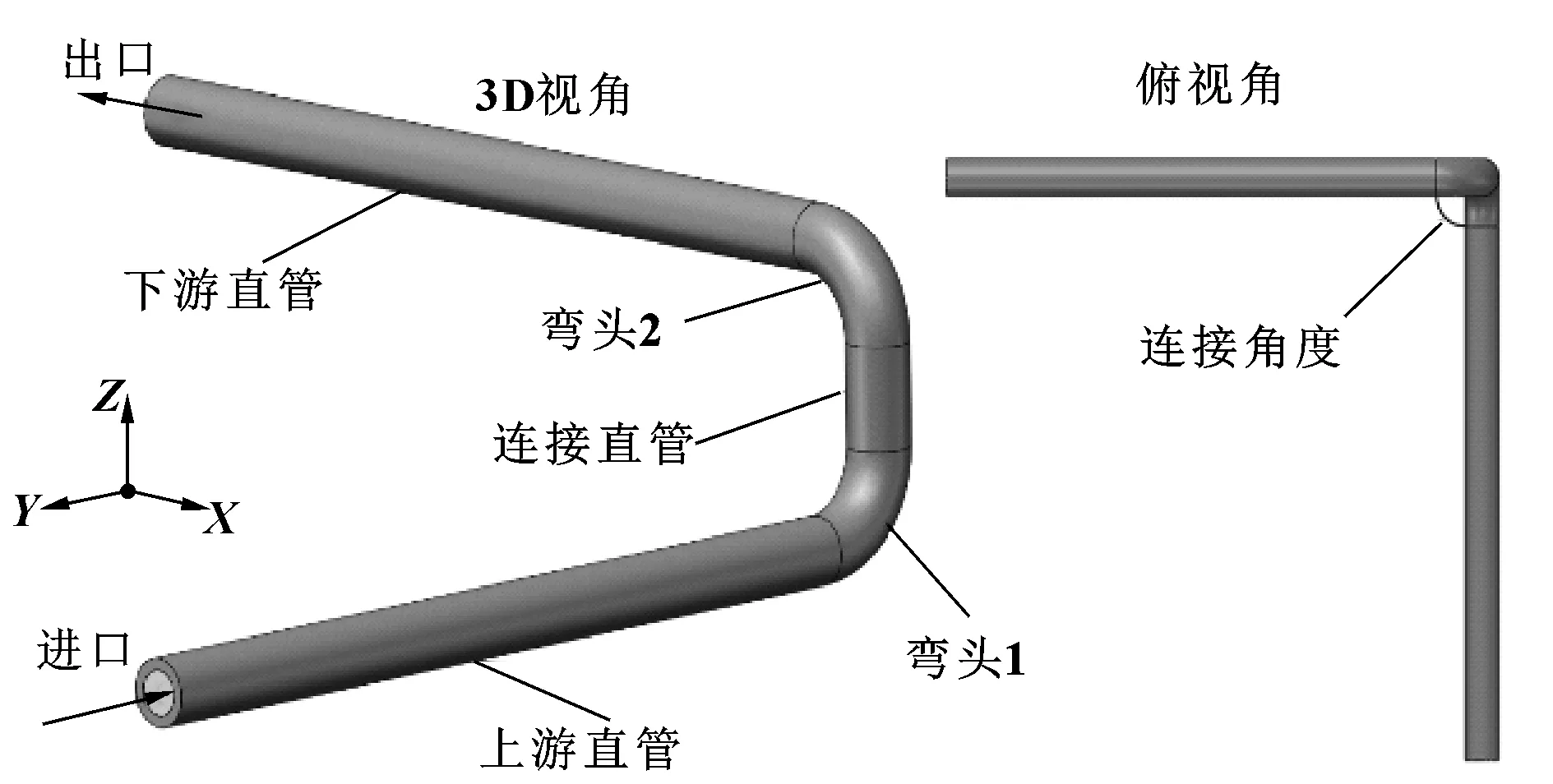
图1 双弯头结构三维模型示意Fig 1 3D schematic of double-elbow structure

文中使用多区域扫掠法分别对流场区域及管壁结构区域进行六面体网格划分。为确定合适的网格数量，开展了网格无关性验证。分别计算了4种不同网格尺寸下弯管的最大冲蚀率(Emax)，结果如表1所示，可以看出，Emax的最大差异出现在M1和M2网格之间，而其最小差异出现在M3和M4网格之间。出于平衡结果准确性和节省CPU计算时间的考虑，文中的所有仿真模型均使用M3网格尺寸，流场和管壁计算域网格划分如图2所示。

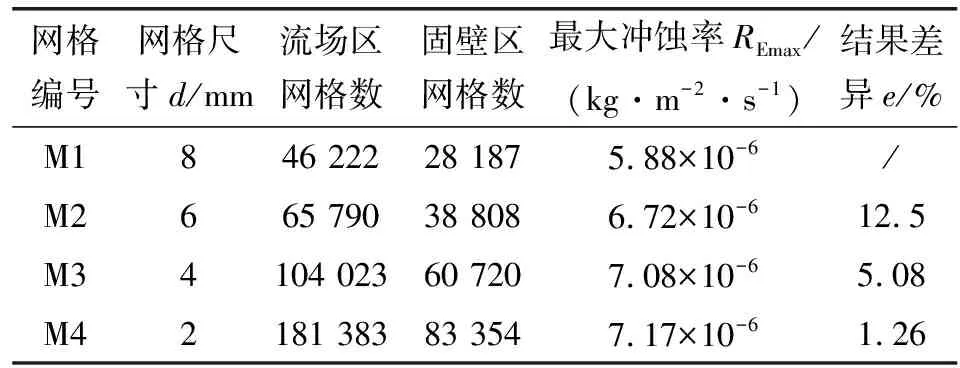
表1 网格无关性验证(Di=70 mm， Lc=1.5 Do，θ=90°)Table 1 Grid independence verification (Di=70 mm， Lc=1.5 Do，θ=90°)

2 流固耦合模拟设置

2.1 流固域边界条件

根据压裂现场实际工况，建立了流场的边界条件。管道入口和出口边界分别设为速度进口和压力出口。进口流量为35 m3/h,湍流强度设置为5%，并以与液体相同的速度均匀地注入球形颗粒，对颗粒-壁面碰撞采用反射条件。流场中液体和颗粒的参数如表2所示。出口压力设定为80 MPa以模拟高压环境。对于管壁结构，其内壁设置为FSI耦合边界，并考虑为无滑移。管道进出口边界设置为固定支撑。管壁材料选用35CrMo钢，其密度为7 850 kg/m3，弹性模量为212 GPa，泊松比为0.286。

表2 压裂液中液体和颗粒参数Table 2 Fluid and particle parameters

2.2 数值模拟方法

数值模拟在ANSYS Workbench平台上完成。分别在FLUENT和ANSYS力学分析模块中对流体和固体域进行计算。并在System coupling模块中完成了这2个区域之间的双向FSI计算，得到了流场和结构场的计算结果。在流体域中，将RNGk-ε湍流和DPM模型应用于流场中。冲蚀数学模型选择塔尔萨大学提出的E/CRC模型[12]，所使用模型数学方程为

(1)

式中：E为冲蚀速率;C是通过冲蚀试验得出的经验常数，其值可以通过试验结果进行修改(E/CRC模型中给出的C=2.17×10-7);HB为材料布氏硬度;Fs是颗粒形状系数;up是颗粒速度;n是速度指数(n=2.41);F(θ)是冲击角多项式方程。

在空间离散设置中，压力项和对流项可以基于二阶离散格式和二阶迎风格式进行处理。此外，在内壁设置动态网格，以适应流固耦合边界上的网格变形。在流固界面上，以耦合边界上的力和位移作为变量进行迭代计算，时间步长设为0.001 s，计算在1.0 s后完成，并将完成的仿真结果用于研究。

3 计算结果及分析

3.1 仿真模型验证

为验证仿真模型准确性，将所建立的基于E/CRC方程的冲蚀计算模型与ZENG等[13]开展的一项X65弯管固液两相冲蚀试验进行了比较。试验开展在一个环路管道系统中，流动的携砂液流速为4 m/s，颗粒尺寸为400～500 μm，颗粒密度为2 650 kg/m3。试验结束后，利用阵列电极测量沿弯头(内径50 mm)外侧中心线几个不同点位的冲蚀率。文中依照文献[13]开展的冲蚀试验参数，利用所建立的CFD仿真模型得到了弯头外侧中心线的冲蚀率分布结果。根据试验结果修正公式(1)中的经验常数C为1.16×10-8。图3显示了仿真预测结果和试验结果的对比，可以看出，模拟值与试验值具有较好的吻合性。

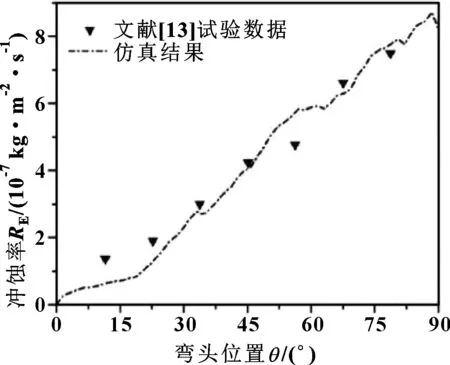
图3 模拟与试验结果对比Fig 3 Comparison of simulation and test results

3.2 压裂工况下双弯头管汇冲蚀结果

对参照案例的结果进行分析，图4所示为流场整体压力分布和2个弯头处的速度分布。可以看出，直管内压力分布均匀，但2个弯头内有明显的压力梯度，最大和最小的压力分别出现在弯头的外侧和内侧。图5展示了2个弯头进出口截面处的二次流矢量，由于弯头处存在径向压力梯度，高速流动的压裂液通过2个弯头时会形成涡流，涡流引起的二次流随主流继续发展。在离心作用和二次流的作用下，颗粒主要对弯头外侧进行冲击，所以弯头的冲蚀主要是发生在其外侧，特别是靠近弯头处。

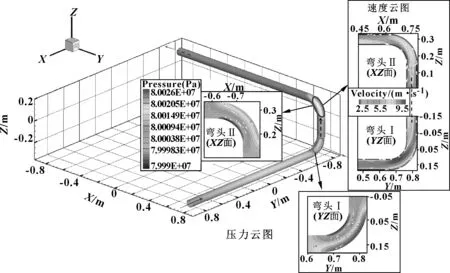
图4 流场压力和速度分布Fig 4 Pressure and velocity distribution of double-elbow

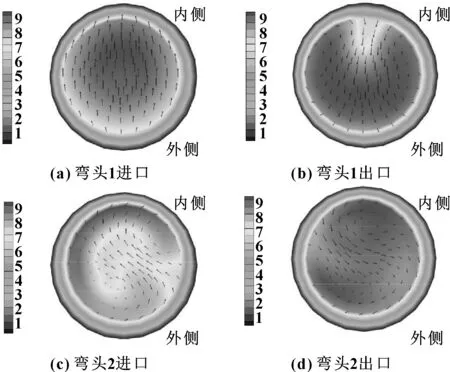
图5 截面二次流矢量Fig 5 Secondary flow vector in a cross-section normal to thepipe axis at the first elbow entrance(a);the firstelbow exit(b);the second elbow entrance(c)；the second elbow exit(d)

双弯头管汇的冲蚀率云图及颗粒轨迹如图6所示，可以看出，第二个弯头的冲蚀程度高于第一个弯头。这种现象可以通过分析颗粒轨迹得到解释，虽然一些颗粒在第一个弯头外侧处积聚，并由于惯性力的作用对外侧管壁进行冲击，但是由于离心力和流体对颗粒的拖曳力作用下，大部分颗粒会随着流体沿着连接直管的外侧流动并流至第二个弯头处。由于流体运动方向发生了2次变化，更多的颗粒将积聚在第二个弯头处，从而第二个弯头相比第一个弯头受到更多颗粒的冲击，导致第二个弯头的冲蚀更严重。因此在现场检测时，应该更注意对第二个弯头的冲蚀情况进行检测，避免出现由冲蚀磨损带来的管道损伤。

图6 冲蚀率云图和颗粒轨迹Fig 6 Erosion rate contour and particle trajectory

双弯头管汇的流致变形云图如图7所示，可以看出，2个弯头和连接直管的管壁受流体作用下的变形较大。另外，从图7还可以发现，由于离心力和压力梯度的影响，弯头外侧受到更大的流体动力作用，从而管壁外侧的变形大于内侧。

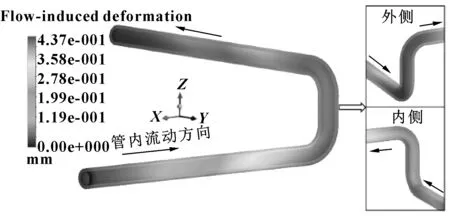
图7 管壁流致变形分布Fig 7 Flow-induced deformation of the double-bend

3.3 双弯头连接直管长度对冲蚀结果的影响

不同连接直管长度Lc的双弯头管汇冲蚀率云图如图8、9所示。当Lc≤4Do时，随着连接直管长度增加，冲蚀率逐渐降低，这是由于随着连接直管长度增加，颗粒在流经第一个弯头后发展更加充分，在第二个弯头处积聚的颗粒数减少，从而降低了第二个弯头的冲蚀率。在这过程中，双弯头最大冲蚀率随着连接直管长度增加呈线性下降的趋势。

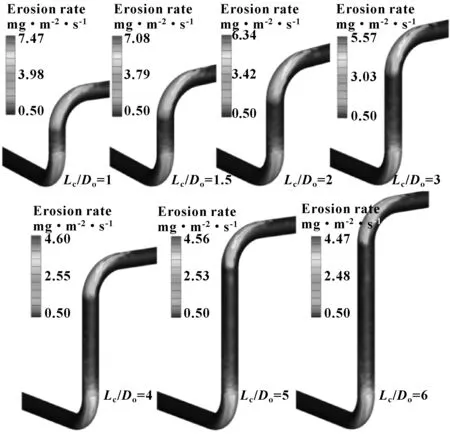
图8 连接直管长度对冲蚀率的影响Fig 8 Effect of connection straight pipe length on flow erosion

图9 不同连接直管下最大冲蚀率曲线Fig 9 The maximum erosion rate versus withconnection straight pipe length

当Lc>4Do时，随着连接直管长度的增加，冲蚀率变化不大，这是由于当直管长度足够大时，管内流动充分发展。另外，随着第二个弯头冲蚀率的降低，2个弯头的最大冲蚀率逐渐接近。

不同连接直管长度下双弯头管汇的流致变形情况如图10所示。由于结构系统刚度的变化，管件变形程度随着连接直管长度的增加而增大。最严重的变形(dmax=0.505 mm)发生在最长连接直管长度处(Lc=6Do)。不同连接直管下最大流致变形如图11所示，可以看出连接直管长度和冲蚀率之间的关系可拟合为二次多项式。

图10 连接直管长度对流致变形的影响Fig 10 Effect of pipe inner diameter on flow-induced deformation

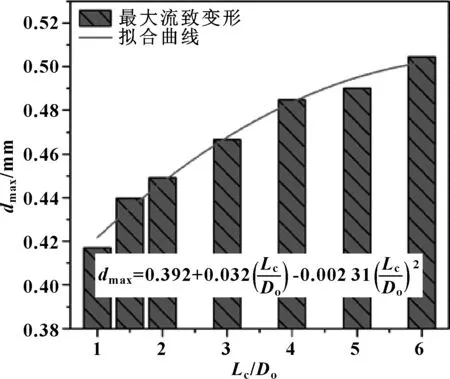
图11 不同连接直管下最大流致变形曲线Fig 11 The maximum deformation versus withconnection straight pipe length

综合考虑冲蚀率和流致变形结果，2个弯头之间的连接直管长度宜设计为Lc=4Do。这样可以在不发生严重的流致变形情况下，有效降低双弯头的冲蚀磨损破坏。

3.4 管道内径对冲蚀结果的影响

不同内径下的双弯头管汇冲蚀率云图如图12所示，管道内径变化对其冲蚀程度影响很大。随着管径增大，双弯头管汇冲蚀率逐渐降低，最小内径(Di=50 mm)时，冲蚀率为7.21×10-5kg/(m2·s)，是最大内径(Di=90 mm)时的约65倍，这种由内径差异带来的较大冲蚀率变化可以从两方面得到解释:一方面，管道内径增大会导致弯头外侧遭到颗粒冲击的面积随之增大，从而降低管壁遭受冲蚀破坏的程度;另一方面，在相同的进口流量下，管道内径的减小会导致流速的迅速增大，从而使冲击到管壁的颗粒带有更大的动能。不同管内径下的最大冲蚀率如图13所示，可以看出，双弯头的冲蚀严重程度随着管道内径的增大呈幂指数衰减。

图12 管内径对冲蚀率的影响Fig 12 Effect of pipe inner diameter on flow erosion

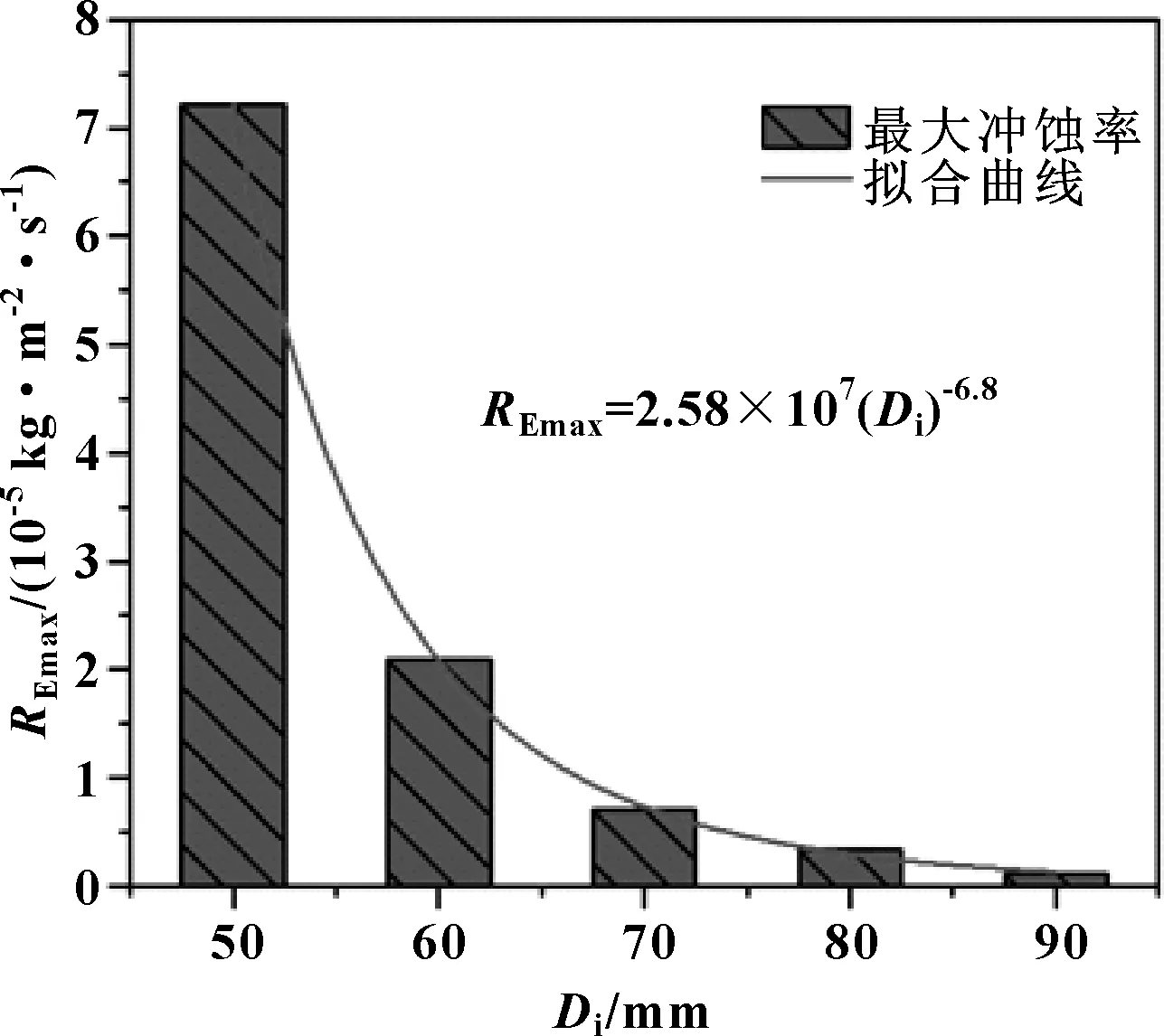
图13 不同管内径下最大冲蚀率曲线Fig 13 The maximum erosion rate versus with pipe inner diameter

管内径对双弯头流致变形结果影响如图14所示，随着管径增大，流致变形增大。这个结果可根据管道弹性力学理论进行解释，在壁厚相同的情况下，承受高内压载荷的管壁，其应力随着管道内径增大而增大，从而使管道变形程度增大[14]。不同管径下的流致变形结果如图15所示，随着管道内径从50 mm增大到90 mm，其最大变形呈线性增大，管壁最大变形从0.296 mm增大到0.632 mm。

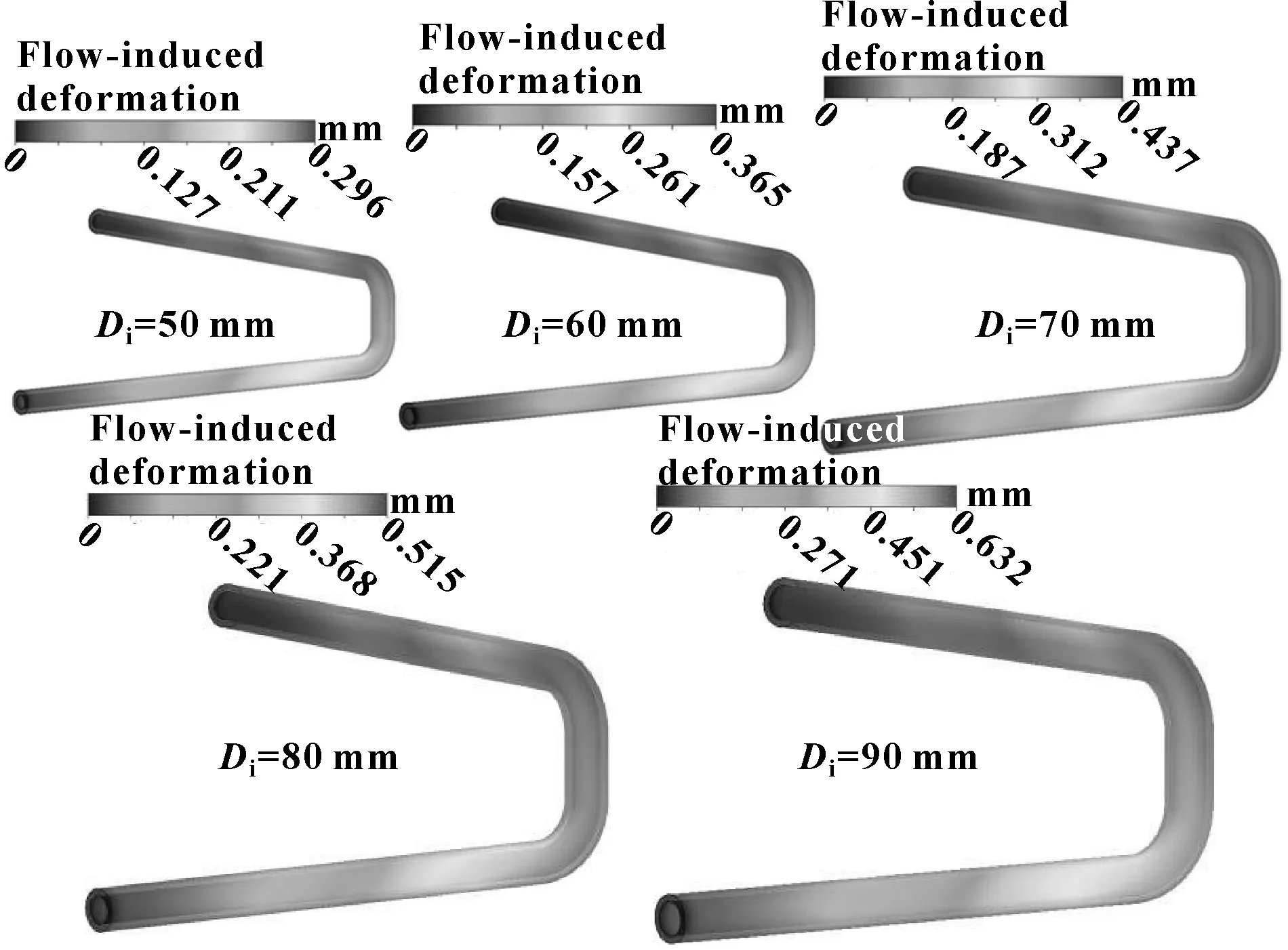
图14 管内径对流致变形的影响Fig 14 Effect of pipe inner diameter on flow erosion

图15 不同管内径下最大流致变形曲线Fig 15 The maximum deformation versuswith pipe inner diameter

3.5 双弯头连接角度对冲蚀结果的影响

通过改变2个弯头之间的连接角度，可以使流体经过双弯头管汇的流动方向发生改变，不同连接角度的双弯头管汇冲蚀率变化和颗粒轨迹如图16所示。可以看出，当连接角度为0°时，冲蚀最为严重。这是由于在这种情况下，2个弯头的外侧均在同一方向上，大部分颗粒流经第一个弯头后会沿着连接直管对第二个弯头外侧进行冲击。相反，当连接角度为180°时，沿着连接直管流向下游的颗粒仅有少部分会积聚在第二个弯头处，使得第二个弯头冲蚀程度降低，从而导致整个管件冲蚀严重程度下降。

图16 弯头间连接角度对冲蚀率的影响Fig 16 Effect of fluid turning direction on flow erosion

双弯头管汇的流致变形结果如图17所示。系统结构刚度随着双弯头连接角度的变化而变化，连接角度为90°时会造成最大的变形。将2个弯头从异面改为同面后，变形程度下降。综合考虑冲蚀率和变形结果，双弯头管汇的连接角度设计为0°是最为合理的。

图17 弯头间连接角度对流致变形的影响Fig 17 Effect of fluid turning direction onflow-induced deformation

4 结论

(1)当2个弯头之间的连接直管长度Lc≤4Do时，双弯头管壁最大冲蚀率随着连接直管长度增加而减少。当Lc>4Do时，流动发展充分，连接直管长度对冲蚀率的影响不大。对于流致变形，双弯头结构的变形随着连接直管长度增加而增加。综合考虑冲蚀磨损和变形结果，双弯头之间的连接直管宜设计为Lc=4Do。

(2)管道内径的变化对双弯头的冲蚀和流致变形影响很大，随着内径的增大，冲蚀率呈幂指数下降，但同时会导致变形程度增加。综合考虑两者影响，对于双弯头管汇，其管内径不宜过大或过小。

(3)双弯头之间的连接角度变化对冲蚀磨损和流致变形程度也有影响，当2个弯头之间的连接角度为0°时，其冲蚀和变形程度均为最低。