应力符号规定的差异与注释
马文国,张 刚,杨有贞
(1.宁夏大学 物理与电子电气工程学院,宁夏 银川 750021;2.宁夏大学 固体力学研究所,宁夏 银川 750021;3.宁夏大学 学术期刊中心,宁夏 银川 750021)
物理量的精确描述需要对具体的研究对象进行量化处理,一般需要进行大小或方向的约定,使其后续的使用更符合常识和逻辑。在材料力学、弹性力学和土力学中,应力符号的规定略有不同,给教学和研究中相关问题的理解带来了一些不便,主要的原因是研究应力的方法有所差异。
材料力学中应力符号的规定未按坐标轴方向进行约定[1—3],而是根据内力求解应力,规定沿截面外法线方向的应力为正应力,能使研究对象发生顺时针转动趋势的应力为正剪应力[1—3]。弹性力学中应力的正负是与坐标系方向有关,若某截面的外法线方向与坐标轴正方向一致,就称该截面为一个正面,该面上的应力以沿坐标轴正方向的规定为正,负面上沿着坐标轴负方向的应力规定为正,反之为负,正应力和剪应力均适用于此规定[4—5]。弹性力学与材料力学所规定的正应力的正负号一致,即以拉应力为正,压应力为负。这两种力学规定的剪应力参考正方向有差异,材料力学中每个面上的两个剪应力总是一正和一负成对出现,而弹性力学中每个面上的剪应力均为正值。这种规定上的差异容易使初学者陷入理解误区。土力学应力符号规定与弹性力学完全相反[6—7]。这种规定主要是考虑到土是一种受静水压力影响的压硬性地质材料,以压应力为正的规定更适合描述土力学的特点。
材料力学中剪应力符号规定是按照力偶矩平衡问题进行推导的,由此推导出了剪应力互等定理,但应该重视基于剪应力的力偶矩的矢量性,即微元体承受两个大小相等方向相反的力偶矩。这种力偶矩矢量性表明了剪应力至少在材料力学的体系中不存在矛盾或者错误,是建立于客观基础上的物理规律,理论上也是自洽的,这和材料力学中一点的应力状态规定的剪应力的正负性没有矛盾的地方。材料力学中采用该规定可以方便使用应力圆(莫尔圆)进行问题的几何求解。同一个受力体系在弹性力学中的规定虽然和材料力学有所差异,但是剪应力作用产生的效果是完全一样的,剪应力体现在力偶矩的正负上,不同体系采用了不同的表示方法而已。本文综合分析了三种力学应力符号的规定、主应力及主方向表达式的差异,并采用应力张量表示一点的应力状态,进一步明确了材料力学、弹性力学和土力学在本质上都是统一的。
1 应力符号的规定
1.1 三种力学应力符号规定的示意图
图1a、图1b 和图1c 分别给出了材料力学、弹性力学和土力学中一点的三向应力状态。图1 仅给出了三个正面上的受力状态,另外三个面的应力状态完全和正面相反,材料力学和弹性力学的正应力规定受拉为正。图1a,材料力学中的剪应力τxy,τyz,τzx规定为正,τyx,τzy,τxz规定为负。图1b,弹性力学中的τxy,τyz,τzx,τyx,τzy,τxz均为正,并且材料力学与弹性力学中τxy,τyz,τzx规定的正方向相反,这是形成误区的根源。图1c,土力学中的所有应力均规定为正,此规定和弹性力学完全相反,正应力的正负号规定以压为正,剪应力的正负号规定是,在与坐标轴一致的正面上,方向与坐标轴方向相反的为正,反之为负。为理解三种力学中应力符号规定的差异,简单起见,采用平面应力讨论一点的应力状态,不论是哪种力学的符号规定,对应的结果都是一致的。
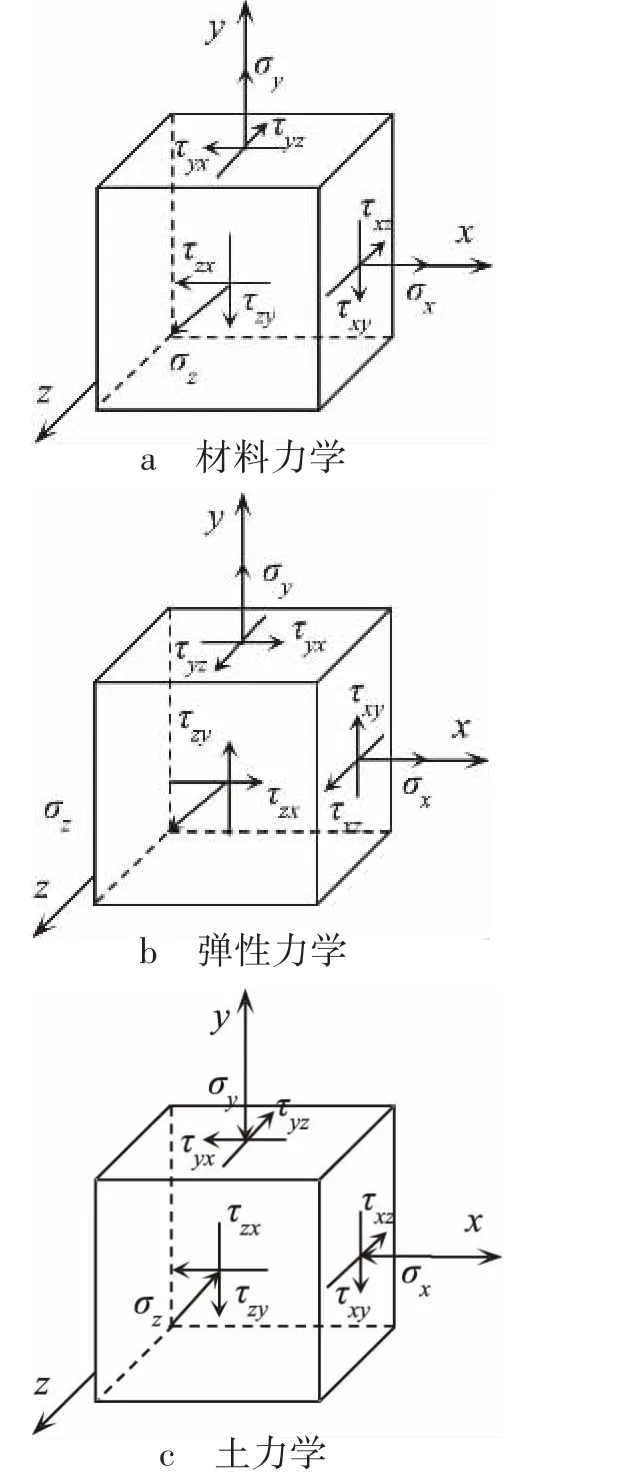
图1 材料力学、弹性力学和土力学对应的应力状态
1.2 平面应力状态下材料力学中斜截面上的应力
材料力学中的剪应力互等定理是从微元体力偶矩平衡推导出剪应力在数值上是相等的,剪应力是矢量,对单元体产生力偶矩,该力偶矩可以看作是一种广义的作用力和反作用力,大小相等,方向相反,如图2a 所示。一点的应力状态的解析法或图解法(莫尔圆法)中规定了剪应力对单元体内任意点的力偶矩为顺时转向时规定为正,如图2 所示,τxy为正,τyx为负,即剪应力互等关系为τxy=-τyx。该应力符号的规定和坐标系没有关系,正应力和截面外法线一致的规定为正,剪应力使得单元体产生顺时针旋转的规定为正,应强调剪应力是以力偶矩的矢量形式进行标定的[1—3,8—9]。同时规定从x 轴逆时针旋转到单元体任意斜截面的法线方向的角度α 为正,根据应力单元的受力特点,α∈[-π/2,π/2]。
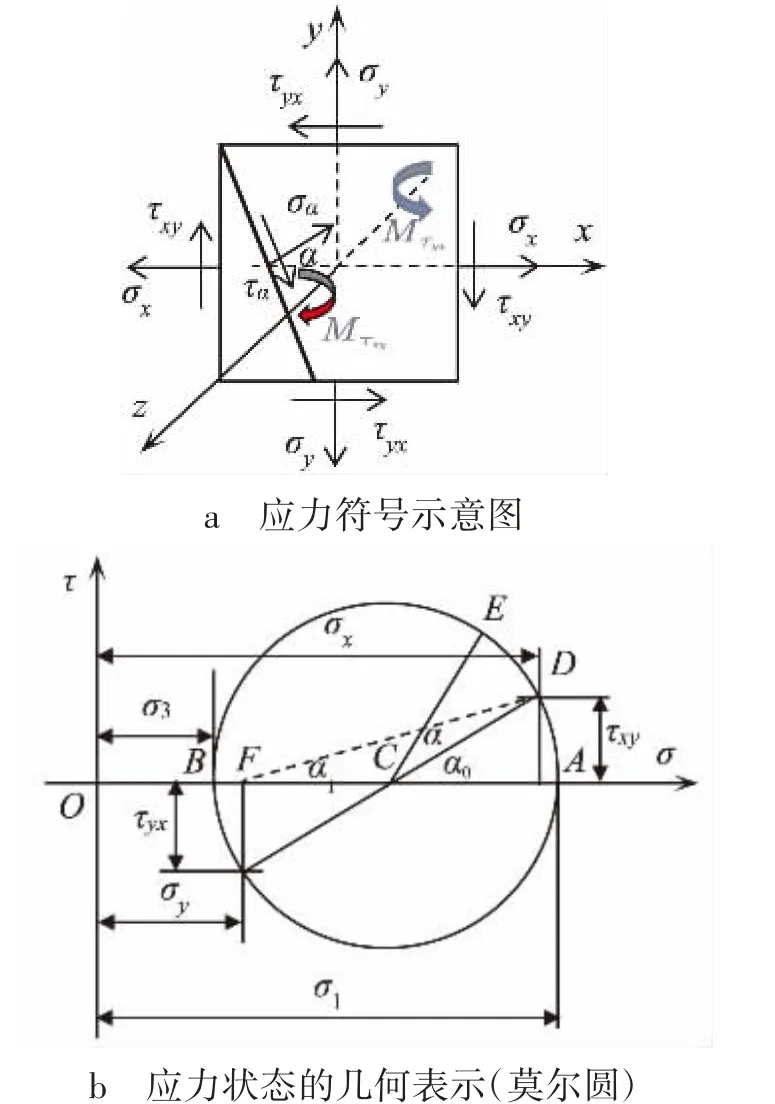
图2 平面应力状态下材料力学应力符号与莫尔圆
这些规定的优点是可以借助Mohr 提出的应力圆来确定一点的应力状态,是一种几何方法,相对于解析法,简单直观,不用记公式,物理意义明确,容易理解和应用,在工程精度要求不高的条件下,莫尔圆是一种非常完美的求解方法。缺点是在没有计算机绘图的条件下,没有解析法那样精确,不能有效地扩展到三维一般应力问题的求解,并且三向应力状态下,一般需要事先通过解析法求得三个主应力的大小,然后才能获得任意斜截面上的应力状态,也不能直接确定主应力的方向。
平面应力状态下,图2a 单元体斜截面法线与x 轴夹角为α 的正应力、剪应力和主应力方向可以根据图2b 的应力圆求解,三者的表达式分别为式(1)~(3):
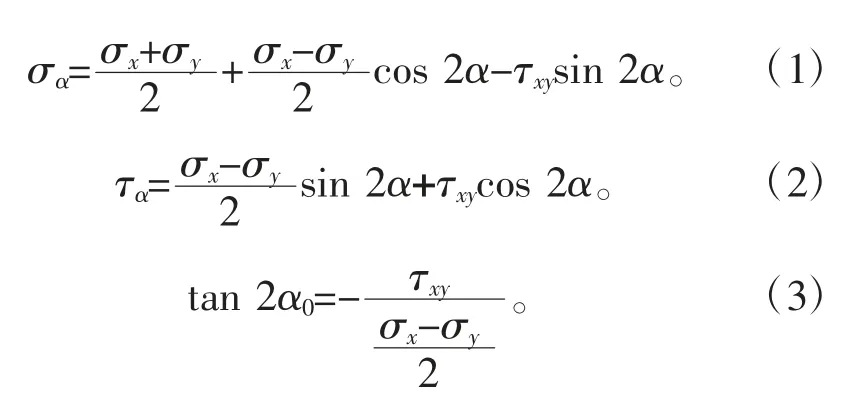
1.3 平面应力状态下弹性力学中斜截面上的应力
弹性力学和材料力学的应力符号的差异主要在于弹性力学中的应力符号与坐标系相关。弹性力学中的正应力与材料力学中的规定是一致的,而剪应力的规定有差异[10]。弹性力学规定,在正面上(外法向与坐标轴方向一致的面),剪应力与坐标轴正方向一致的为正,在负面上(外法向与坐标轴方向相反的面),剪应力与坐标轴负方向一致的为正;图1b 中空间单元体上的正应力和剪应力均为正值,与材料力学中剪应力符号的规定有差异,此时剪应力互等关系为τxy=τyx。在平面应力状态下(图3),仅给出应力单元体,不能再使用莫尔圆求解,若要使用莫尔圆求解,必须切换到材料力学的约定。弹性力学根据任意斜截面法线方向与坐标轴的方向余弦求解微元体的x 和y 方向的平衡方程,并将此平衡方程投影到该斜截面的法线方向和切线方向,即可以获得该斜截面上的正应力和剪应力表达式,分别为式(4)和式(5)。
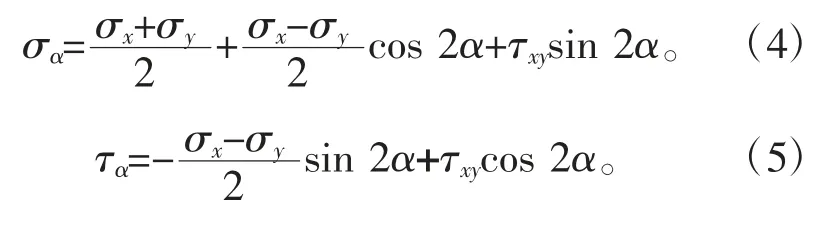

图3 平面应力状态下弹性力学应力符号
弹性力学中主应力方向和材料力学表达式形式有差异,通常在斜截面上使得剪应力等于零,求解平面应力状态下的主应力后获得最大主应力方向,几何上表示为如图2b 中α1,表达式如式(6)所示。这和材料力学中确定主应力的方法是一致的,只是表示主应力方向的习惯不同而已,本质完全一样。
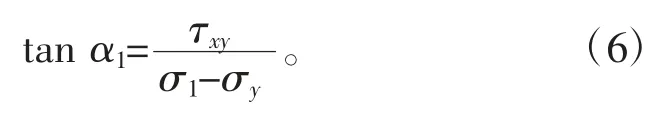
材料力学和弹性力学在剪应力的正方向的规定有差异,此差异将导致材料力学和弹性力学推导出同一斜截面上的不同应力计算公式和主应力方向。从式(1)、式(2)、式(4)和式(5)可以看出任意斜截面上的应力表达式的不同,弹性力学和材料力学在斜截面上的应力公式在带有sin 2α 的项上有差异。主应力方向分别采用圆心角2α0和角度α1进行表示。材料力学中的最大主应力方向(式(3))完全由单元体的受力状态直接可以求解。而弹性力学中最大最小主应力的计算公式通常使斜截面上的剪应力等于零,得出主应力求解公式,一般先确定主应力σ1后再确定主应力的方向。从式(3)和式(6)可以看出,材料力学和弹性力学求得的主应力方向也不一样。
弹性力学中正应力和剪应力是和坐标系相关的,这种定义有利于说明一点的应力沿着某个方向,在笛卡尔坐标系中沿着x,y 和z 的分量的具体值。这种标定方法的优点是方便使用连续介质力学或应力张量对一点的应力状态进行描述,剪应力虽然都是正值,但是产生的力偶矩和材料力学是完全相同的,没有本质的差异,对三维问题同样适用。缺点是在平面应力状态下使用莫尔圆求解仍然需要切换为材料力学的约定。
1.4 平面应力条件下土力学中斜截面上的应力
土力学中关于应力符号的规定与弹性力学完全相反,这是根据地质类材料的力学特性进行的一种约定,土是一种具有压硬和摩擦特性的材料,相对于金属材料在受力过程中通常会出现明显的体积变化。根据图1c 所示,图4 给出了平面应力条件下土力学的应力符号和斜截面应力平衡分析的示意图。

图4 土力学应力符号和斜截面的应力平衡
图4 中的正应力和剪应力均为正值,斜截面的外法线与x 轴的夹角为α,求解主应力和主方向使用莫尔圆更为直接,此时,剪应力的符号规定与材料力学相反,即以使单元体有逆时针转动趋势时为正。斜截面上的正应力和剪应力使用σα和τα来表示,假设斜截面的面积为dA,侧面和底面的面积分别为dAcos α 和dAsin α,把作用于截取部分的应力投影于斜截面的外法线和切线方向,所得平衡方程为

根据剪应力互等定理,τxy和τyx在数值上相等,以τxy替换τyx,并简化式(7)和式(8)得:
式(9)和式(10)与弹性力学中斜截面上的正应力与剪应力表达式式(4)和式(5)完全一样。这里根据土力学的受力特性进行了斜截面上正应力和剪应力的推导,斜截面上的正应力σα和剪应力τα都是α的函数。而式(9)、式(10)与材料力学中的公式有所差异。对式(9)、式(10)的角度α 求导可得极值,并确定主应力方向。
对公式(9)的α 求导,得:
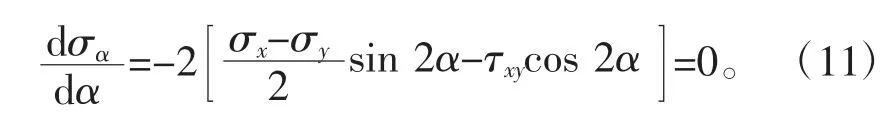
当α=α2时,能使式(11)中,则在α2所确定的截面上,正应力即为最大值或最小值,所以最大或最小主应力所在的方位为
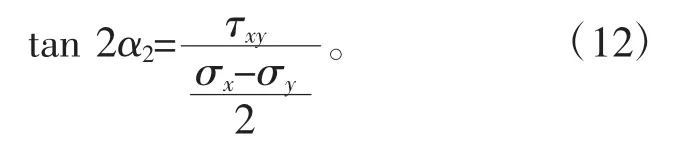
式(12)与材料力学的主应力方向表达式式(3)相差一个负号。由式(12)可以求出相差π/2 的两个角度α2,它们确定两个相互垂直的平面,分别是最大正应力和最小正应力所在的平面。由式(12)求出相应的正弦和余弦值,可求出相应的最大和最小正应力为

一般约定σx是截面单元上数值较大的那一个,即σx≥σy,公式(12)确定的两个α2中,绝对值较小的一个确定σ1所在的平面。
根据公式(1)~(13)可以看出,材料力学、弹性力学和土力学分别有各自的应力符号体系,虽然形式上有所差异,但本质上是统一的。
2 张量形式的统一理解
根据1.1~1.3 节的描述,无论是材料力学、弹性力学还是土力学,主要是剪应力的符号规定有所差异,但是剪应力产生的力偶矩具有相同的效果。这可以从材料力学中一点的应力状态的图解法(莫尔圆)及弹性力学和土力学中一点的应力状态的张量形式进行说明。材料力学中的莫尔圆如图2b,弹性力学和土力学中的应力张量如下式:
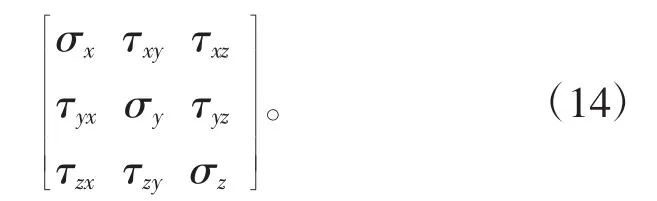
材料力学中的一对剪应力产生大小相等、方向相反的力偶矩,但在莫尔圆中直接使用τxy=-τyx,主要因为莫尔圆采用了标量化的几何方法,把应力的大小和方向在莫尔圆上用长度和相对应的夹角分开表示,剪应力产生的效果已经体现在剪应力的正负值上,本质上体现了剪应力产生的力偶矩的平衡。由图2a 可知:

在平面应力状态下,弹性力学和土力学中采用的张量形式(式(14))的二维情况如下式:

式(16)分别是平行于x 和y 方向的应力矢量,这里主要讨论τxy和τyx产生的力学效果。张量中的任何分量都是矢量,矢量把大小和方向放在一起考虑,这里不能像莫尔圆中直接把剪应力写成τxy=-τyx,因为剪应力已经具有各自的方向性,否则会出现剪应力使得单元体发生旋转而产生加速度的问题,会产生和剪应力互等定理强调的力偶矩平衡相互矛盾的结论。所以不论是材料力学、弹性力学或土力学,使用莫尔圆和张量形式求解一点的应力状态都完全是协调的,不存在任何矛盾,只是学科发展中有着自己的规范而已。在通常的平面应力计算中,莫尔圆比张量形式更直观简洁,但是张量表示的应力状态在代数上更完备,更适合于三维应力空间问题的求解。
3 结论
(1)本文对材料力学、弹性力学和土力学中应力符号规定的合理性和统一性进行了比较详细的说明,材料力学中应力符号的规定主要来自于截面上内力的集度与法线的一致性和剪应力使单元体的旋转趋势来确定应力符号的正负,这种规定与坐标系无关。弹性力学中应力符号的规定完全依赖于坐标系,正(负)面上的应力和坐标轴正(负)向一致的为正,相反为负。土力学的应力符号体系完全与弹性力学相反,主要是为了描述地质类具有压硬和剪胀性材料而采取的合理方法。
(2)平面应力状态下,一点的应力状态无论采用材料力学中的应力圆还是弹性力学中的应力张量表示,都能得出相同的结果。应力圆对应力状态的求解直观,容易理解。应力张量求解主应力及其方向在数学上有严密的理论体系,但是相对于应力圆求解应力状态更复杂一些。三向应力状态下,应力张量求解主应力和主方向相对应力圆的图解法更为合理。
(3)在土力学应力符号规定与弹性力学完全相反的体系下,推导了一点的应力状态的主应力及其方向,土力学与弹性力学主应力的表达式完全相同。土力学与材料力学主应力方向的表达式相差一个负号。

