基于产量水肥利用效率对滴灌西兰花水肥制度的优化

陈华斌，田军仓，2，3*，沈 晖，2，3，刘大铭

西兰花是重要的经济蔬菜作物之一[1—2]。西兰花种植中，为了追求经济效益，水肥浪费现象极其严重[3—8]。灌水量、施肥量是影响植物生长的主要因素，是作物提质增效的关键[9—15]。近年来，国内一些学者研究了灌水量、施肥量对作物生长指标及光合、产量和品质的影响[9，13，16]。为了确定灌水量对西兰花的影响，赵鹏志等[4]通过二因素三水平随机区组试验，得到西兰花产量最高、光合指标最高、品质最好的水肥组合为灌水量2 175 m3/hm2、施肥量1 200 kg/hm2。张辉等[17]采用双因素交互试验设计寻找适宜当地西兰花的水氮组合，结果表明，灌水量为田间持水量的60%，硝态氮与铵态氮比例为5∶5 时，西兰花的产量、水氮利用效率、干重等表现最优。李录山等[18]寻找西兰花最优水肥组合，结果表明，中水中肥，西兰花产量最高，保护酶系统活性较高，最适宜当地作物生长要求。

目前，对滴灌西兰花水肥最优组合的确定多为水肥二因素三水平。为了适应宁夏本地环境，本文进行膜下滴灌西兰花二元二次正交旋转组合试验，确定最适合本地种植西兰花的滴灌灌水量和追肥量组合，为西兰花提质增效提供科学依据。

1 材料与方法

1.1 试验地概况

试验于2020 年7—9 月份在宁夏银川市贺兰县永兴村试验基地进行（106°32′E，38°39′N）。试验地年平均气温10.92 ℃，年平均日照时数2 620.5 h，年平均降水量186.4 mm。其中，生育期降水量为113 mm。土壤类型为沙壤土，0～20 cm 土壤干容重为1.34 g/cm3，pH值为8.11，碱解氮为59 mg/kg，有效磷为30.2 mg/kg，速效钾为167 mg/kg，0～60 cm 土壤田间持水率为21.43%。

西兰花品种为“耐寒优秀”，其基肥为友谊复合肥（N-P2O5-K2O，15-15-15），整地覆膜时均匀撒施300 kg/hm2。采用文丘里施肥器进行水肥一体化随水追肥，肥料为心连心尿素（w（总氮）≥46%）、俄罗斯阿康公司生产的复合肥（N-P2O5-K2O，16-16-16）。西兰花采用膜下滴灌，滴灌带直径16.0 mm，滴头间隔35 cm，滴头流量1.6 L/h。

1.2 试验设计

采用二元二次正交旋转组合试验，选取灌溉定额W 和纯追肥量F 两个因素，每个因素设置1.414，1，0，-1，-1.414 五个水平，试验共16 个处理，每个处理重复3 次，共计48 个小区。T9～T16 是同一处理的重复，重复间差异体现试验田位置不同和环境差异产生的误差。每个处理为1 条垄，分上、中、下3 个小区，每个小区对应1 个重复，旨在研究不同水肥组合对宁夏贺兰县西兰花生长、产量和品质的影响。

根据已有试验的研究经验并结合当地的农业生产情况，确定灌溉定额和施肥量的上下限分别为3 045 m3/hm2和1 305 m3/hm2，2 152 kg/hm2和922 kg/ hm2。各因素水平（Xpj）和变化间隔（Δj）为

式中：X1j表示因素的下限；X2j表示因素的上限；j 为因素个数；γ 为星号臂。二元二次通用旋转组合试验方案见表1。

表1 西兰花种植试验方案设计

注：表中纯追肥量包括氮肥量、磷肥量和钾肥量。

试验田长44 m，宽35 m。每垄对应1 个试验处理，每个处理分上、中、下3 个小区，小区长11 m，宽0.8 m，面积为8.8 m2。西兰花种植方式为温室内育苗，育苗完成移栽至试验田内，移栽时间为2020 年7 月21 日，收获时间为2020 年9 月21—30 日。西兰花采取垄上移栽种植，垄面宽80 cm，垄沟宽40 cm，垄高20 cm，每垄上种植2 行西兰花，垄上覆黑色地膜，株距为35 cm。西兰花灌溉方式为膜下滴灌，采取2 行1 管模式，滴头间距为35 cm。6 月25 日育苗，四叶一心时定值，移栽时间为7 月21 日。

1.3 检测指标及方法

（1）产量及品质的测定。西兰花采收期每个处理选取上、中、下3 个小区，小区长为11 m，采收小区内西兰花，测量其鲜重，并折算成每公顷产量。维生素C 按照钼蓝比色法测定，可溶性糖按照蒽酮比色法测定，可溶性蛋白采用考马斯亮蓝G-250 染色法测定，硝酸盐采用紫外分光光度法测定，可溶性固体按照阿贝折射仪测定。

（2）灌溉水分利用效率计算。

式中：IWUE为灌溉水分利用效率，kg/m3；Y 为产量，kg/hm2；TW为总灌水量，m3/hm2。

（3）偏氮肥生产力计算。

式中：PNP为偏氮肥生产力，kg/kg；Y 为产量kg/hm2；TF为总追氮量，kg/hm2。

1.4 数据处理

数据统计用Excel 2010，显著性检验和方差分析用Spss 26（Tukey 法和LSD 法），线性回归及其检验用DPS 7.05，相关图形绘制使用Origin2018。

2 结果与分析

2.1 不同水肥处理对西兰花产量和水肥利用率的影响

由表2 可知，T1 西兰花产量最高为25 668 kg/hm2；T6 次之，产量为24 766 kg/hm2；最低为T3，产量为18 690 kg/hm2。由T5 与T9～T16 比较可以看出，在施肥量为1 537 kg/hm2时，灌水量由1 305 m3/hm2增加到2 175 m3/hm2时，西兰花产量增加明显。T1和T2 相比，可以发现当灌水量为2 790 m3/hm2，施肥量从1 103 kg/hm2增加到1 972 kg/hm2时，对西兰花产量影响显著（P＜0.05），说明灌水量为2 160 m3/hm2时，西兰花产量随着施肥量的增加而增加。由T1 与T9～T16 比较可以看出，当灌水量和施肥量分别由2 175 m3/hm2、1 537 kg/hm2增加到2 790 m3/hm2、1 972 kg/hm2时，T1 处理的西兰花产量和T9～T16 处理差异显著（P＜0.05），说明在T1 的水肥组合下西兰花产量最高。T1 较CK 增加了8.4%，T3 较CK 降低了26.7%。

不同水肥处理西兰花灌溉水分利用效率和偏氮肥生产力见表2。T5 灌溉水分利用效率最高为14.32 kg/m3，T6 灌溉水分利用效率最低为8.13 kg/m3。由T5 与T9～T16 比较可知，同一施肥水平下，灌溉水分利用效率随灌水量的增加而减少。T5 比CK增加了31.5%，T6 比CK 降低了25.3%。T7 偏氮肥生产力最高，为39.79 kg/kg，T3 偏氮肥生产力最低，为18.89 kg/kg。由T8 与T9～T16 比较可知，同一灌水量下，偏氮肥生产力随施肥量的减少而增加。T7比CK 增加了45.4%，T3 比CK 降低了31.0%。2.1.1 回归方程的建立

表2 不同水肥处理对西兰花产量、灌溉水分利用效率和肥料偏生产力的影响

2.1.2 回归方程的显著性检验 经方差分析可知，F回归=13.53，F0.05（5，10）=3.326，F回归＞F0.05（5，10），显著水平P=0.005 1，则回归方程的F 检验显著，表明根据试验数据建立的回归方程可靠，具有应用价值；回归方程相关系数R2=0.90，拟合程度好。

2.1.3 回归系数的显著性检验 采用t 检验法进行回归系数显著性检验。结果表明，一次项中灌溉定额x1和二次项中施肥量x2对西兰花产量影响极显著，其他项均不显著。回归方程可化简为

2.1.4 主因素分析 主因素分析主要是分析灌溉定额、施肥量对西兰花产量的影响效应。试验所建立的回归方程中2 个因素均为规范变量，偏回归系数不受因素取值大小和单位的影响，其绝对值的大小可以直接反映各个因素对西兰花产量的影响程度。由表3 可知，水肥因素对西兰花产量的影响大小为灌溉定额x1＞施肥量x2。其中，灌溉定额对西兰花产量影响极显著，说明该试验条件下，灌溉定额是主要因素。

表3 回归系数t 检验结果

2.1.5 单因素分析 对式（5）进行降维处理，即将回归方程中的灌溉定额、施肥量中的2 个因子固定在零值，即可求得单因素对西兰花产量的一元二次回归模型：

式中：y1，y2分别为单独考虑灌溉定额和施肥量对应的估计值，kg/hm2。令xj分别为-1.414，-1，0，1，1.414，通过式（7）～（8）计算得出相应的预测产量，可分别得出单因素不同水平对产量的曲线效应图（图1）。

由图1 可知，产量随着灌溉定额的增加而增加；当施肥量编码小于0 时，产量随着施肥量的增加而增加；当施肥量编码大于0 时，产量随着施肥量的增加而降低。

图1 单因素对产量的影响

2.1.6 交互作用分析 灌溉定额与施肥量的交互作用见图2。由图2 可知，产量受灌水量和施肥量的交互影响，当灌水量一定时，产量随着施肥量的增加先增加后减少，当施肥量编码值为0 时，产量达到最大值；当施肥量一定时，产量随着灌水量的增加而增加。通过模型寻优发现灌水量、施肥量编码组合为（1.414，0），即灌水量为3 045 m3/hm2，施肥量为1 537 kg/hm2时，西兰花产量最高可以达到26 658 kg/hm2。

图2 灌溉定额与施肥量的交互作用

2.2 不同水肥处理对西兰花品质的影响

由表4 可知，维生素C 的质量比在T1 时最大，为705 mg/kg；在T3 时最小，为612 mg/kg；T1 比T3提高了7.8%，T3 处理比CK 降低了6.9%。可溶性糖的质量比在T1 时最大，为41.5 mg/g；在T3 时最小，为19.8 mg/g；T1 比T3 提高了109.6%，T1 比CK 提高了14.6%。可溶性蛋白的质量比在T8 时最大，为6.4 mg/g；在T6 时最小，为3.9 mg/g；T8 比T6 提高了64.1%，T8 处理比CK 提高了20.7%。可溶性固体质量分数在T8 最大，为10.17%；在T6 最小，为7.98%；T8 比T6 提高了27.4%，T8 处理比CK 提高了16.1%。硝酸盐的质量比在T3 时最大，为1 392 mg/kg；在T9时最小，为765 mg/kg；T3 比T9 提高了81.9%，T3处理比CK 提高了44.8%。

表4 不同水肥处理对西兰花品质的影响

综上所述，T1 处理的维生素C、可溶糖的质量比最高，可溶性蛋白的质量比、可溶性固体质量分数都较好，硝酸盐一般。

2.2.1 回归方程的建立

2.2.2 回归方程的显著性检验 经方差分析可知，F回归=9.02，F0.05（5，10）=3.326，F回归＞F0.05（5，10），显著水平P=0.012 7，则回归方程的F 检验显著，表明根据试验数据建立的回归方程可靠，具有应用价值；回归方程相关系数R2=0.85，拟合程度好。

2.2.3 回归系数的显著性检验 采用t 检验法进行回归系数显著性检验。结果表明，一次项中灌溉定额x1和二次项中施肥量x2对西兰花中维生素C 的影响极显著，其他项均不显著。回归方程可化简为

2.2.4 主因素分析 主因素分析主要是分析灌溉定额、施肥量对西兰花维生素C 的影响效应。试验所建立的回归方程中2 个因素均为规范变量，偏回归系数不受因素取值大小和单位的影响，其绝对值的大小可以直接反映各个因素对西兰花中维生素C的影响程度。由表5 可知，水肥因素对西兰花中维生素C 的影响大小为灌溉定额x1＞施肥量x2。其中，灌溉定额对西兰花中维生素C 影响极显著，说明该试验条件下，灌溉定额是主要因素。

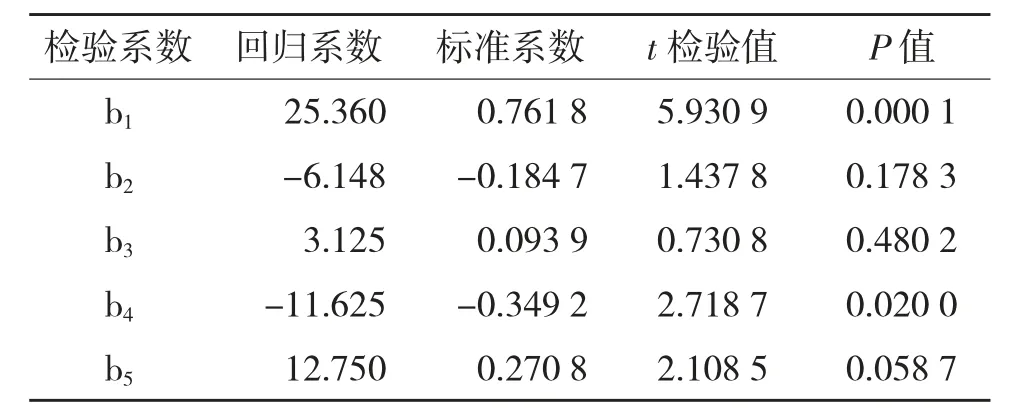
表5 回归系数t 检验结果

2.2.5 单因素分析 对式（9）进行降维处理，即将回归方程中的灌溉定额、施肥量中的2 个因子固定在零值，即可求得单因素对西兰花中维生素C 的一元二次回归模型：

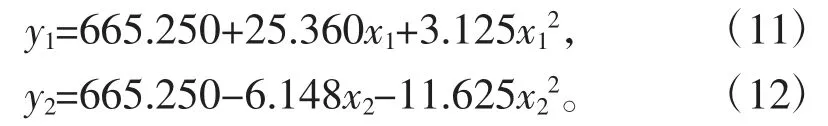
式中：y1，y2分别为单独考虑灌溉定额和施肥量对应的估计值，mg/kg。令xj分别为-1.414，-1，0，1，1.414，通过式（11）～（12）计算得出相应的预测维生素C，可分别得出单因素不同水平对维生素C 的曲线效应图（图3）。

由图3 可知，维生素C 的质量比随着灌溉定额的增加而增加；当施肥量编码小于0 时，维生素C随着施肥量的增加而增加；当施肥量编码大于0 时，维生素C 随着施肥量的增加而降低。

图3 单因素对维生素C 的影响

2.2.6 交互作用分析 灌溉定额与施肥量的交互作用见图4，维生素C 受灌水量和施肥量的交互影响，当灌水量一定时，可以看出维生素C 的质量比随着施肥量的增加先增加后减少，当施肥量编码值为0时，维生素C 的质量比达到最大值；当施肥量一定时，维生素C 的质量比随着灌水量的增加而增加。

图4 灌溉定额与施肥量的交互作用

通过模型寻优发现灌水量、施肥量编码组合为（1.414，1），即灌水量为3 045 m3/hm2，施肥量为1 972 kg/hm2时，西兰花维生素C 的质量比最高可以达到708 mg/kg。

3 结论

（1）在T1 时，西兰花产量最高，为25 668 kg/hm2；T3 最低，为18 690 kg/hm2。灌溉水分利用效率在T5时最高，为14.32 kg/m3；在T6 时最低，为8.13 kg/m3。偏氮肥生产力在T7 时最高，为39.79 kg/kg；T3 时最低，为18.89 kg/kg。

（2）在T1 时，维生素C、可溶性糖的质量比最大，分别为705 mg/kg，41.5 mg/g；在T3 时最小，分别为612 mg/kg，19.8 mg/g。在T8 时，可溶性蛋白的质量比、可溶性固体质量分数最大，分别为6.4 mg/g，10.17%；在T6 时最小，分别为3.9 mg/g，7.98%。硝酸盐质量比在T3 时最大，为1 392 mg/kg，在T9 时最小，为765 mg/kg。

（3）建立了灌水量及施肥量对西兰花产量、维生素C 质量比的影响模型，模型达到显著水平，对试验最优水肥组合进行验证，结果有很好的重现性，表明模型准确。通过验证，得到灌水量是影响西兰花产量、品质的主要因素，施肥量是次要因素。

综合上述分析，从西兰花产量、水肥利用效率、品质及回归模型寻优水肥组合可以得到，在降水量为113 mm 时，灌水量为2 790～3 045 m3/hm2，施肥量为1 537～1 972 kg/hm2时，可以获得较高的产量（2 6147.72～2 6657.88 kg/hm2）及较优的西兰花品质（维生素C 质量比为707.52～710.40 mg/kg），是适宜本地西兰花种植推广的较优水肥组合方案。