面向车辆目标的路侧多摄像机双向匹配交接方法*

陈 明，武一民，高博麟，郑凯元

（1.河北工业大学机械工程学院，天津300130；2.清华大学车辆与运载学院，北京100084）

前言

随着智能网联汽车云控系统和智能交通系统的快速发展，路侧感知成为了车路协同感知的重要组成部分，在提高感知精度、扩大感知范围等方面发挥着不可或缺的作用［1］。其中在复杂环境中利用摄像机跟踪运动目标是路侧感知中十分具有挑战的问题。目前单摄像机下的目标跟踪方案相对成熟，但受制于有限的视野范围，基于单摄像机的目标跟踪无法覆盖更大的区域。与此同时，大量摄像机往往独立工作，各个摄像机之间对于目标的感知信息不能被充分利用，导致同一目标在不同摄像机间被识别为不同身份，为构建目标的全局轨迹增加了困难。而多摄像机目标跟踪技术通过利用两个或两个以上的摄像机，根据摄像机部署关系与目标信息，对视野中的同一目标进行身份一致性标记，从而实现跨视野、长时段的目标连续跟踪。

根据摄像机间视野的分布情况，研究可分为有重叠视野与无重叠视野两个方面。在有重叠视野方面，目前主要采用的研究方法有3类。（1）基于特征匹配的目标交接法通过提取目标的某一外观特征，或融合多个外观特征，对目标之间的外观相似程度进行度量，将相似度较高的两目标进行匹配。所选取的外观特征包括颜色［2］、轮廓［3］、纹理［4］等，但由于不同摄像机间视角及亮度存在差异，同一目标的特征在不同相机间可能会存在较大的差异，影响匹配准确率。（2）基于环境信息与摄像机标定的交接方法通过对三维环境建模和标定摄像机信息，建立相机与场景的映射关系，将目标映射至同一坐标系下进行目标交接［5-6］。但这类方法从信息的获取难度和计算的复杂程度都比较大，实现起来较为困难。（3）基于视野分界线的目标交接方法是一种简单有效的方法，自Khan等［7］提出摄像机视野分界线是进行目标交接的重要基础后，很多研究人员采用同步视频［8］、特征点匹 配［9］等 方 法结合L-M（levenbergmarquardt）［10］、随 机 采 样 一 致 性（random sample consensus，RANSAC）［11］算法来不断优化投影矩阵，以准确地恢复视野分界线，进而根据目标点与分界线的位置关系，对目标进行筛选，从而实现目标交接。这类方法易于实现，但忽略了目标与目标之间的关系，在面对目标密集的场景时，交接的准确性会受到影响。综上所述，现有重叠视野内的目标交接方法一般利用目标的位置、外观信息进行交接，但路侧视角下车辆目标交接由于场景复杂，目标密集，现有方法存在一定缺陷，需做出进一步改进。

针对上述问题，本文中提出基于双向匹配的车辆目标交接方法。通过建立两个具有重叠视野的摄像机的投影关系，生成视野分界线并划分重叠视野，将重叠视野内的目标经投影后基于目标间的位置信息进行双向的匹配，根据提出的双向匹配矩阵与矩阵标识符输出匹配结果。为了应对多个目标间距较近时仅依靠位置信息无法区分目标的问题，引入车辆目标的外观特征，根据颜色直方图度量车辆外观的相似度，以提高目标交接准确性。

1 单应矩阵

具有重叠视野的摄像机，其公共视野内的目标在无遮挡情况下可同时被两个摄像机检测并投影为坐标系下的同一坐标点，因此目标的位置信息是交接过程中的主要特征之一。通过求解单应矩阵，可划分重叠视野以确定需要交接的感兴趣目标，并建立目标在摄像机间的投影关系。

当图像中的三维场景点处在近似平面的平面上（如地平面）或在低视差的区域中，可通过单应矩阵，将处在重叠视野的该场景点从一个图像平面上映射到另一图像平面上［12］，如图1所示。

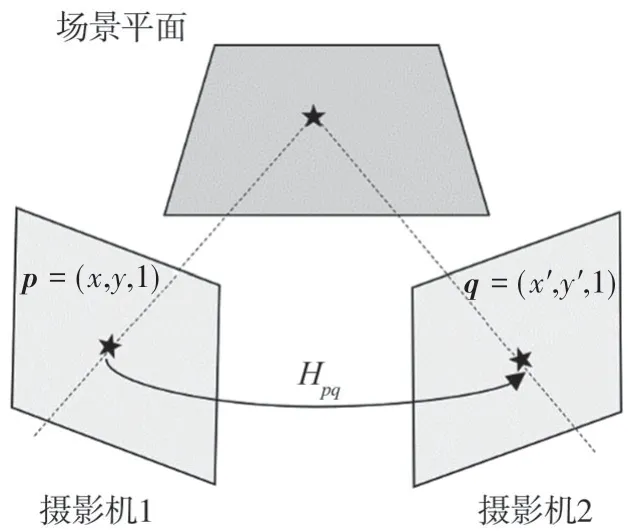
图1 单应变换示意图

假设某一实际场景中有一三维场景点处在地平面上，其在摄像机1视野中的像素坐标点为p=(x，y，1)，在另一摄像机2视野中的像素坐标点为q=(x’，y’，1)，则有如下变换关系：

即

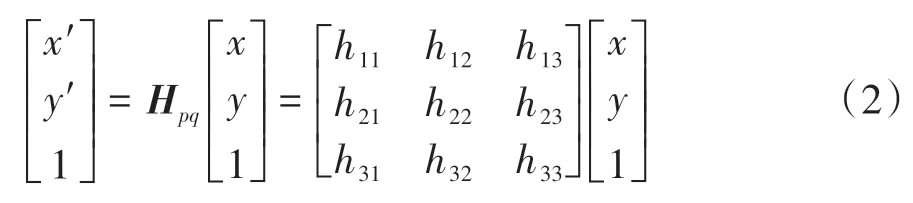
其中单应矩阵Hpq是3×3的非奇异矩阵，具有8个自由度，至少需要4对匹配的坐标点对，就可计算出单应矩阵。在计算单应矩阵时，研究人员普遍采用尺度不变特征变换（scale invariant feature transform，SIFT）、加速鲁棒特征（speeded up robust features，SURF）等方法来获得用于计算单应矩阵的特征点。但在路侧视角下的道路场景中效果并不理想，原因主要有三：首先，单应矩阵实际上是平面到平面间的映射，当摄像机的视野中存在多个平面时，所得的单应矩阵并不准确［13］；其次，在道路场景中，路侧摄像机视角下的道路表面通常具有较为均匀的纹理，往往无法有效地提取出足够多的特征点；此外，道路表面存在大量形状、颜色相似的车道线与标识线，导致在对数量较少的特征点进行匹配时，还会存在较多误匹配，最终无法准确计算单应矩阵。

因此采用如下方式：假定两相邻摄像机编号为i和j，在两摄像机的重叠视野内，选取不共线的4个标定点，在摄像机i视野中表示为P1、P2、P3、P4，摄像机j的视野中为P'1、P'2、P'3、P'4。将标定点代入式（2）中计算出摄像机i到摄像机j的单应矩阵Hij，另由下式

可求解摄像机j到摄像机i的单应矩阵Hji。通过单应矩阵Hij与Hji，可将两摄像机视野平面中的任意一点投影至另一摄像机中。将摄像机i的视野边界点经投影与Hough变换［14］，可生成摄像机i的视野分界线其中E∈{T，B，L，R}，表示摄像机视野的上、下、左、右4条边界，如图2所示，得到两摄像机的重叠视野作为目标交接过程的感兴趣区域。

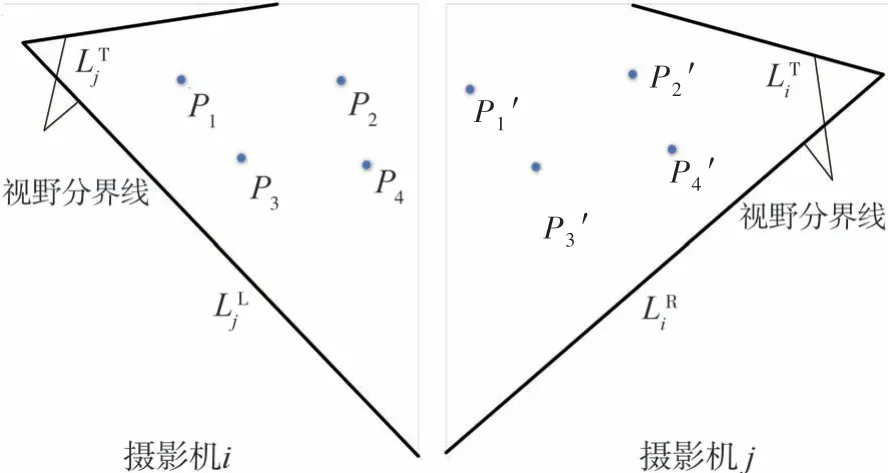
图2 视野分界线与重叠视野示意图

2 双向匹配策略

2.1 单向匹配矩阵

确定单应矩阵与重叠视野后，可根据目标的位置信息对目标进行初步交接。不同于视野分界线法中基于目标点与分界线距离的交接判定方式，本文中更关注目标与目标间的位置关系。通过对待交接目标的检测点进行单应投影，得到待交接目标在另一摄像机视野中的投影点，从而进行交接。

基于单摄像机的目标检测，可得到单帧每个车辆目标的二维检测框。此时如果直接采用检测框中点进行投影，将会形成刺穿点［13］，无法得到该目标正确的中心投影点。因此，选择车辆检测框下框线的中点作为该目标在当前摄像机视野内的检测点，利用式（1）可将摄像机i中该目标的检测点映射至摄像机j的视野中进行匹配，如图3所示。

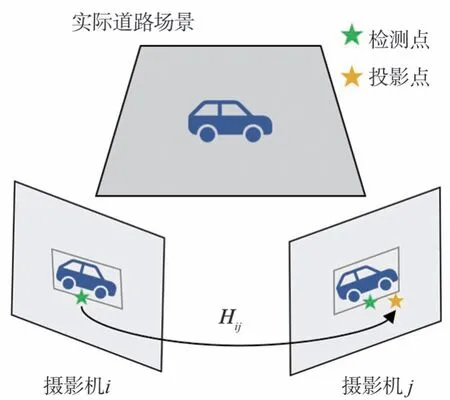
图3 车辆目标投影匹配示意图

由此得到重叠视野内每个车辆目标在图像坐标系下的检测点与投影点位置坐标，然后计算摄像机j中每个待交接目标的投影点与该视角下所有检测点的欧氏距离，得到距离矩阵Dij，公式如下：

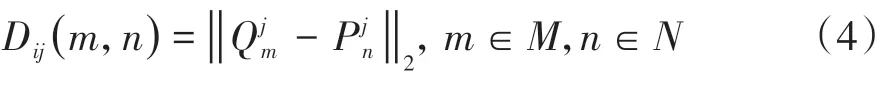
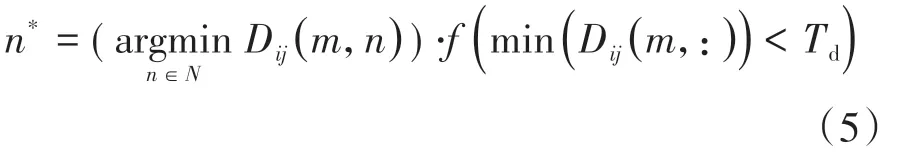
式中：f(∙)为指示函数，若“∙”为真，则取值为1，若“∙”为假，则取值为0；距离误差阈值Td表示匹配过程中对于投影位置误差的容许程度。根据待交接目标与候选目标的单向匹配结果，构造单向匹配矩阵矩阵中元素值按下式确定：即对于判定单向匹配的待交接目标与候选目标，其对应行列的元素为1，否则为0。

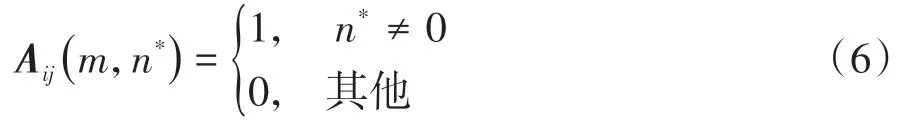
2.2 匹配约束机制

由于目标交接的过程是目标ID间“一对一”的映射关系，单向匹配矩阵应满足［15］：

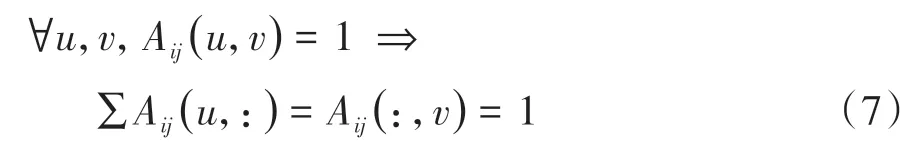
但仅通过上述的单向匹配过程，在目标密集的场景，极易出现两个或两个以上候选目标同时与同一目标进行匹配，出现“多对一”的匹配结果。

为了解决匹配过程中存在的关联冲突问题，使关联过程符合匹配一致性原则，提出一种匹配约束机制：如果第m+1个待交接目标与最近的候选目标的距离小于阈值，判断最近邻的候选目标是否已被前一待交接目标匹配，若未被匹配，则将最近邻的候选目标与当前待交接目标进行匹配。否则，比较匹配冲突的目标对的距离，选取距离最近的目标对进行匹配，另一待交接目标与次近邻的候选目标进行匹配。

2.3 双向匹配

在约束机制下得到的单向匹配矩阵，反映了由摄像机i中的待交接目标投影至摄像机j后的单向匹配结果。但仅依靠目标单向投影后的位置信息进行匹配，效果并不理想，存在较多的错误匹配。为了改善这种情况，提出一种双向匹配策略。该策略的流程如图4所示。

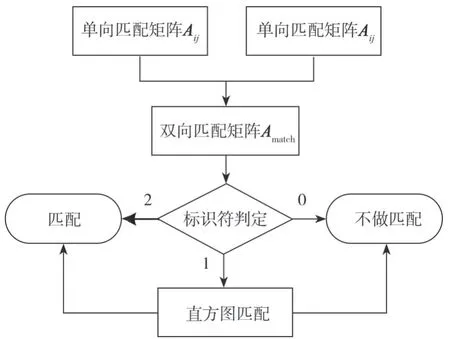
图4 双向匹配策略流程图

按照2.1节和2.2节中的方式将摄像机j中的目标向摄像机i中反向投影，投影过程中采用的单应矩阵由式（2）获得，在约束机制下进行目标匹配并生成单向匹配矩阵AN×Mji，单向匹配矩阵AN×Mji是反向投影（摄像机j到摄像机i）后的目标单向匹配结果。在得到双向的匹配结果后，需要将两次的匹配结果加以综合，从而对每个目标的交接情况做出判断。匹配结果的综合方式由式（8）表示。

Amatch∈{0，1，2}N×M为双向匹配矩阵，矩阵中的每个元素作为匹配标识符，表示双向匹配的判定结果，如式（9）表示：

Amatch(m，n)=2表示双向的匹配结果均判定两目标相匹配，此时判定为同一目标，进行一致性的身份认定；Amatch(m，n)=1表示双向的匹配结果不一致，此时仅依靠目标位置无法做出准确的交接判定，因此，需要进一步依据两目标的外观特征进行验证，并以此作为最终的匹配结果；Amatch(m，n)=0则表示对两目标不做匹配。

3 颜色直方图匹配

在车辆密集的场景下，车辆间距较小，仅依靠目标位置信息进行目标交接，可能因投影过程中的误差，导致错误交接的发生。因此引入目标外观特征，在两次单向匹配结果不一致时，依靠外观相似度进行二次匹配。为使整个算法的计算复杂度不至过高，同时保证对低分辨率图像的匹配结果的鲁棒性，采用车辆的颜色特征，通过提取待匹配目标与候选目标的颜色直方图，经量化后计算目标相似度，进而得出匹配结果。

电子图像在显示时一般用RGB颜色模型，但与人眼对颜色的实际感知有比较大的区别，同样也并不适合用与车辆外观的匹配。本文中采用的HSV颜色模型，是一种与人眼的视觉感知相一致的模型，其通过色调（Hue）、饱和度（Saturation）和亮度（Value）3个与视觉特征有关的量计算描述，更接近于人们对颜色的主观认识，并且对光照的鲁棒性更强，适用于路侧的应用场景。

首先将获取到的RGB模型图像转化为HSV模型［16］：

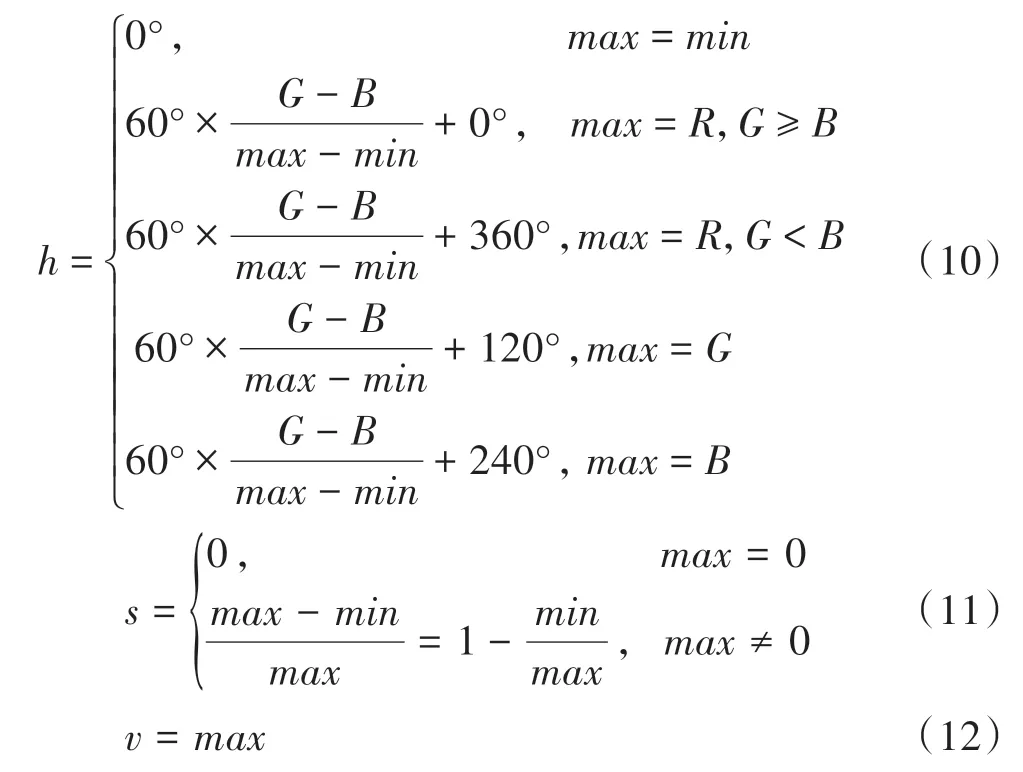
接着将三维分量降维，转化为一维颜色特征向量，计算表达式如下：

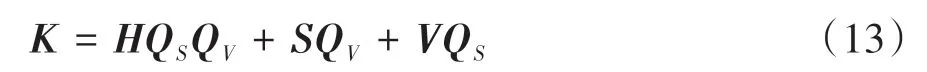
式中：QS与QV分别为S和V分量的量化级数；K为量化后的目标直方图，取值范围是［0，255］。

Bhattacharyya匹配是度量直方图相似性的方法之一，其他方法包括相关匹配、交集匹配等。由于在直方图相似度的所有方法中，这种方法产生了更精确的匹配［17］，因此采用Bhattacharyya法进行度量。Bhattacharyya匹配的表达式如下：

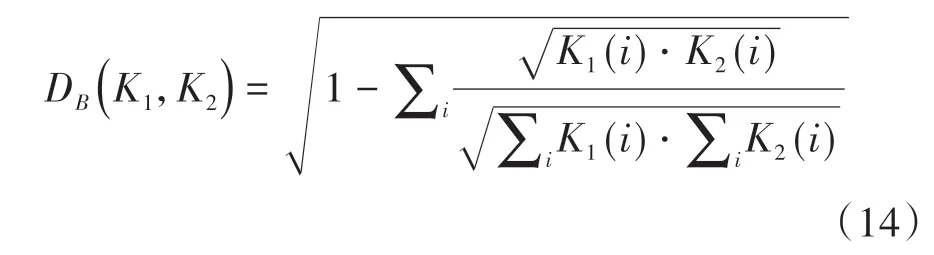
式中：DB为匹配分数；K1为待交接目标的直方图；K2为候选目标直方图。对于匹配得分，分数越低表示匹配的相似度越高。

4 实验验证

为了验证本文算法的有效性，在真实道路中部署4台分辨率为640×480的摄像机，覆盖路段、路口两个场景，摄像机具体的部署情况如图5所示。将单个摄像机下目标检测和跟踪算法处理后得到的数据，包括各个摄像机中车辆的ID以及目标检测框的位置与大小，作为本文实验的输入数据。

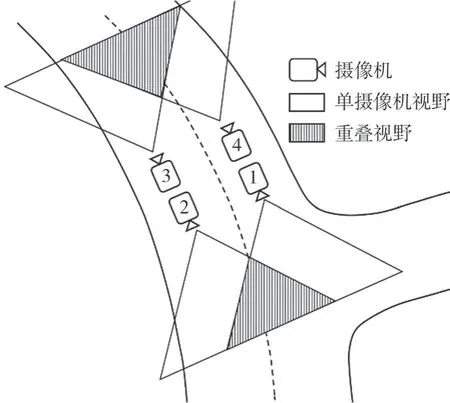
图5 摄像机部署示意图

图6 展示了路口场景的两摄像机在某一帧下的匹配结果。其中图6（a）与图6（b）分别为摄像机1与摄像机2的感知结果，绿色标识为当前摄像机的目标检测点，黄色标识为来自相邻摄像机的投影点，车辆目标的ID已在图中标出。

图6 两摄像机第151帧匹配结果

正确的匹配方式是ID11与21为同一目标，ID12与22为同一目标，而ID为13的车辆由于在摄像机1中被完全遮挡，在当前帧不进行交接。两摄像机对应的单向匹配矩阵如式（15）和式（16）所示。

其中单向匹配矩阵的2行分别对应摄像机1中ID为21与22的2个目标，3列分别对应摄像机2中ID为11、12与13的3个目标，各元素表示目标两两之间的单向匹配结果。可以看到，摄像机1的匹配结果是正确的（目标11与21相匹配，12与22相匹配），但摄像机2的匹配结果中出现了错误的匹配结果（目标13与22误匹配），得到的双向匹配矩阵Amatch如下：

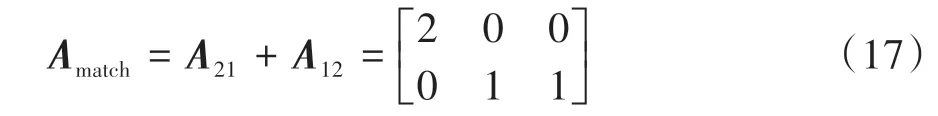
此时摄像机1中ID为22的待交接目标有两个可能的交接目标（目标12与13），计算两种匹配组合的颜色直方图相似度。经计算，待交接目标与两候选目标的直方图匹配分数分别为0.413和0.481，说明候选目标中的前者与待交接目标的直方图差异更小，相似度更高，故依据直方图的二次匹配结果，将ID为12与22的目标相匹配，从而实现正确的目标交接。

为进一步验证方法的有效性，本文中分别统计了两个场景下某一时段车辆目标交接的实验结果。

4.1 路段场景

路段场景下单帧最大车流量为7辆，目标总数为552，剔除误检、漏检的无效帧后，有效帧数为252帧。对路段场景划分其重叠视野后如图7所示。

图7 路段场景

实验选取的指标为漏匹配与误匹配［18］，两指标数值越小，说明方法的漏匹配与误匹配个数越少，匹配的准确度越高，对比方法为单向匹配，其中路段实验结果如表1所示。

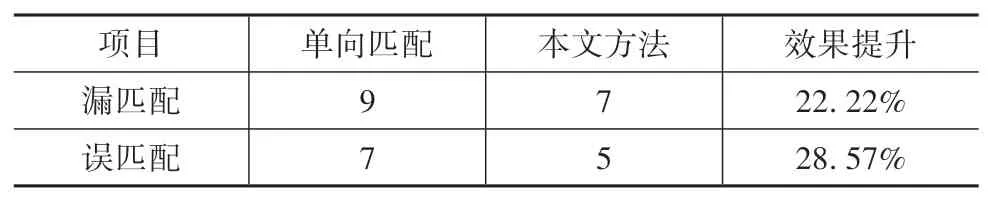
表1 路段场景实验结果

从实验结果可看出，在车辆密度相对较小，道路较为平直的路段场景中，所提出的方法减少了22.22%的漏匹配与28.57%的误匹配，相比于单向匹配结果有显著提升。

4.2 路口场景

路口场景下车辆更加密集，目标数量更多，单帧最大车流量为12辆，有效帧数为259帧，目标总数为892。路口场景划分重叠视野后如图8所示。

图8 路段场景

统计路口场景下所有帧漏匹配与误匹配的结果如表2所示。

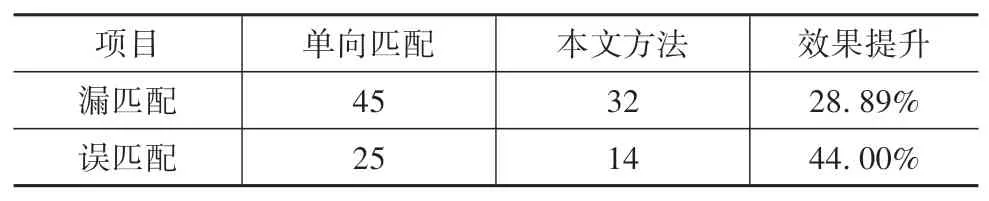
表2 路口场景实验结果

在路况较为复杂的路口场景中，道路物理场景复杂，车辆密度较大，行驶方向多变，增加了目标交接的难度，此时无论是漏匹配还是误匹配，所提出的方法相比于单向匹配都有显著提升，漏匹配降低了28.89%，误匹配降低了44.00%。由此可以看出，本文所提出的方法无论在路况简单的路段场景还是交通环境复杂的十字路口，都可以有效地解决重叠视野下车辆目标的交接问题。

5 结论

为了解决路侧视角下车辆目标在多摄像机间的目标交接问题，提出了双向匹配目标交接方法。利用摄像机间变换关系对重叠域内车辆目标进行投影，并由此设计了双向匹配策略，根据匹配矩阵标识符结合颜色直方图相似度输出结果。经实验验证，所提出的方法对比单向匹配方法，在路段场景下漏匹配降低22.22%，误匹配降低28.57%；路口场景下漏匹配降低28.89%，误匹配降低44.00%。

由于路侧不同部署位置的摄像机间存在着视角差异、亮度变化等挑战，双向匹配交接方法仍有改进之处。匹配过程中距离误差阈值的大小会对漏匹配与误匹配产生趋势相反的影响，通过迭代优化方法求取最优阈值可进一步提高交接准确性。