基于HS⁃FCM模糊聚类的快速多目标车辆跟踪算法*

章军辉，付宗杰，郭晓满，李 庆，陈大鹏，3，赵 野

（1.中国科学院微电子研究所，北京100029；2.江苏物联网研究发展中心，无锡214135；3.无锡物联网创新中心有限公司，无锡214135；4.昆山微电子技术研究院，苏州215347）

前言

实现精准可靠的目标轨迹跟踪是多目标跟踪（multi⁃object tracking，MOT）的主要任务，而强杂波环境下的数据关联、多源数据融合策略等问题一直是MOT领域研究的热难点［1-3］。MOT问题的一般处理流程如图1所示。

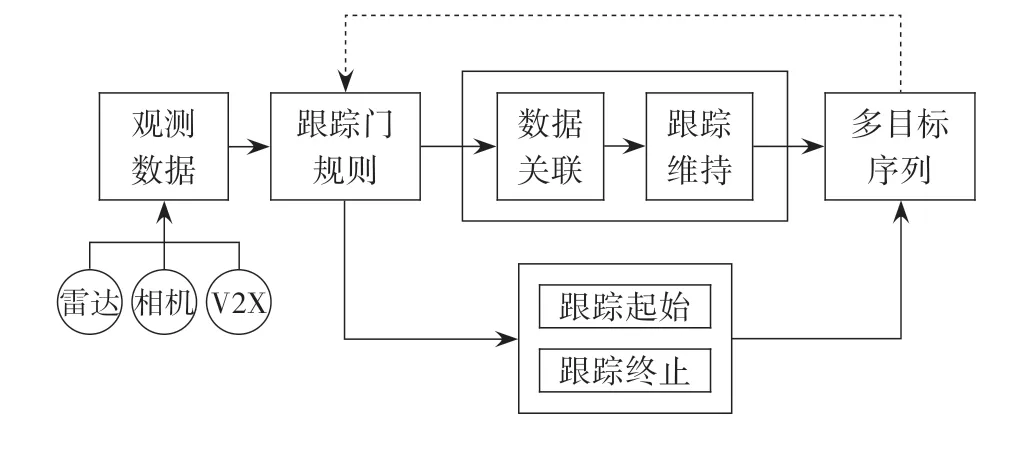
图1 多目标跟踪处理流程

目标的表达通常是采用形状或外观来描述的。对于点表达的目标跟踪问题，点关联的方法主要包括确定性方法与统计性方法。确定性方法通常是在一系列约束条件下寻求关联成本最小化的解，如贪婪搜索法［4］。统计性方法利用位置、速度、加速度等目标的属性来建立状态空间模型，并在一定程度上考虑了模型不确定性以及观测噪声，如联合概率数据关联（joint probability data association，JPDA）［5-6］、多假设跟踪（multiple hypothesis tracking，MHT）［7-8］、概率多假设跟踪（probabilistic multiple hypothesis tracking，PMHT）［9-10］等。对于量测数据落入跟踪门相交区域的情况，将难以确定这些量测是源于哪个目标。基于贝叶斯理论的JPDA算法能够较好地解决杂波环境下相交波门内的量测关联问题，但在跟踪目标数较多或杂波较密集的情况下，存在确认矩阵拆分组合爆炸的现象［6］。基于全邻最优滤波器与Bar-Shalom确认矩阵的MHT算法，通过建立多个候选关联假设，并利用后续的量测来消除当前扫描周期的不确定性，理论上其跟踪效果是相对较优的，不过与JPDA算法一样，其计算复杂度随着目标与量测个数呈指数增长。PMHT算法是基于EM（expectation maximization）策略而设计的，并且认为量测关联过程是相互独立的，故其关联复杂度仅随目标个数呈线性增长，但在标准PMHT算法中所有量测结果皆源于不尽合理的目标假设，所以跟踪效果易受虚假量测的影响。

车辆跟随行驶是日常道路交通环境中最主要的行车工况［11-12］。在强杂波环境下经典数据关联方法的跟踪效果往往不太理想，主要原因如下：①关联概率的计算复杂度较高，影响跟踪效果的实时性［13-14］；②源于不同传感器的数据在时空上存在着较大差异，加大了数据可靠关联的难度［15-16］；③传感器本身的局限性，导致量测存在着一定的不确定性［17-18］。

传统的通过穷举量测-目标所有可能的关联事件或关联假设来估计最优关联的方法，无法完成精确求解，在一定程度上制约了技术的可实施性。考虑到点迹-航迹关联判决本身存在着一定的模糊性与不确定性，本文中发展了一种快速多目标车辆跟踪算法。首先，对多目标车辆跟踪问题进行了数学描述，并建立了相机像素坐标系与世界坐标系的空间映射关系；其次，基于模糊理论将点迹-航迹关联问题转换成量测模糊聚类问题，通过求解各候选量测与聚类中心的模糊隶属度，间接计算出JPDA算法中不确定性量测与各目标的关联概率，再利用概率加权融合对多目标状态进行滤波估计；再次，考虑到机动目标的惯性因素，在车辆密集工况下通过合理调整卡尔曼增益对量测更新进行抑制，以解决目标短暂跟丢问题；最后，通过实车试验对该算法的跟踪效果进行了验证与探讨。

1 多目标观测模型

1.1 数学建模

在车辆跟踪过程中，车辆被视为一种小机动性目标，常用的机动目标运动模型有匀速运动模型、匀加速运动模型等。综合考虑计算实时性与目标的机动性，定义目标运动模型为分段式匀速运动模型，并借助雷达或V2V模块来动态更新各阶段机动目标的纵向速度。此外，对于视觉目标跟踪（visual object tracking，VOT）问题，考虑到相机测距的局限性，将辅以雷达来实时校正车间纵向距离。

1.1.1 多目标观测模型

在多目标车辆跟踪过程中，感兴趣目标（objects of interest，OOI）是位于主车道以及左右车道且距离自车最临近的前方车辆。如图2所示，忽略目标车辆的垂向运动，以自车作为坐标原点，建立车辆水平坐标系。

图2 多目标车辆跟踪的水平坐标系

对于第i个感兴趣的目标车辆，不妨令该目标的纵向距离是di，y(k)，纵向速度是vi，y(k)，横向距离是di，x(k)，横向速度是vi，x(k)，以xi(k)=[di，y(k)，vi，y(k)，di，x(k)，vi，x(k)]T作为状态向量，yi(k)=[di，y(k)，di，x(k)]T作为观测模型输出，建立离散状态空间方程：

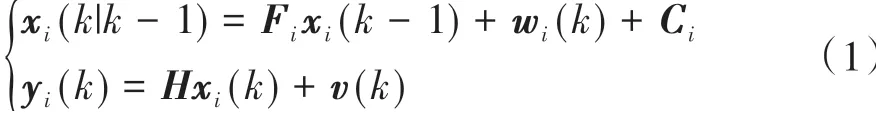
式中：xi(k-1|k)表示基于k-1时刻对k时刻第i个目标的状态预测；yi(k)是对第i个目标的量测预测；Fi是目标i的状态转移矩阵；H是视觉传感器的量测矩阵；Ci是状态校正项；wi(k)是过程噪声；v(k)是视觉传感器的量测噪声。其中，i∈[1，3]是目标标签。

1.1.2 模型参数

假设过程噪声wi(k)为服从N(0，Q)分布，量测噪声v(k)服从N(0，R)分布。多目标观测模型中各系数矩阵满足：

式中：Ts是采样周期；Δvi，y是纵向相对速度，用于定期校正分段式匀速运动模型。

1.2 空间融合

如图3所示，建立相机像素坐标系与世界坐标系的空间映射关系。

图3 相机标定模型

图像数组（即像素坐标）与像平面坐标之间的关系如下：

式中：u、v分别表示像素在图像数组中的列数、行数；(u0，v0)是投影中心点；dx、dy分别表示像素在像平面坐标系中x轴、y轴上的物理尺寸。

像平面坐标与相机坐标之间的关系如下：

式中f是焦距。

相机坐标与世界坐标之间的关系如下：

式中：R3×3=Rx(α)Ry(β)Rz(θ)是旋转矩阵；t3×1是平移向量。α、β、θ分别表示世界坐标系中x轴、y轴、z轴的旋转角，且满足：

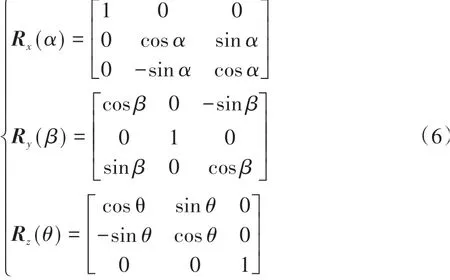
从而，三维世界点P与其在像平面上投影点p的关系满足：

式中：ξ是比例因子；p=[u，v，1]T是二维图像中投影点p的齐次坐标；P=[Xw，Yw，Zw，1]T是三维世界点P的齐次坐标是相机的内参矩阵，用以实现相机3D坐标到2D坐标的转换；[R3×3|t3×1]是相机的外参矩阵，用以实现将点从世界坐标系到相机坐标系的转换。

2 多目标状态滚动估计

2.1 数据关联

数据关联是将源自各传感器的量测数据与相应的目标航迹进行关联的过程。对于回波落入跟踪门重叠区域的情形，引入关联概率，用以表示不确定性量测与各个源目标之间的关联程度。

2.1.1 定义

定义1.马氏距离

定义L维模型预测向量与量测向量之间的马氏距离为

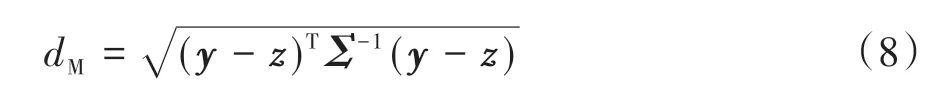
式中：dM是马氏距离；y是模型的预测向量；z是当前周期内的量测向量；Σ是协方差矩阵，且满足

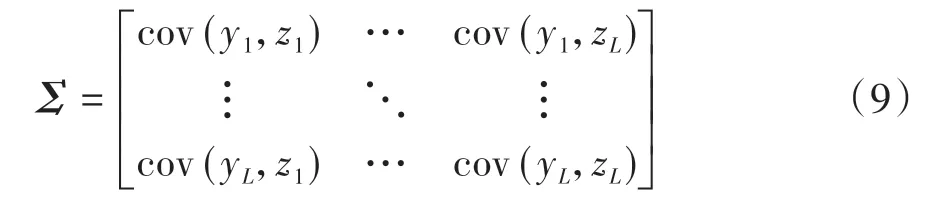
马氏距离是一种加权欧氏距离，当协方差矩阵为单位矩阵时，马氏距离即为欧式距离。由于不同特征的度量标准之间存在着较大的差异，通过欧氏距离来量化评估往往缺乏一定的合理性，而马氏距离在一定程度上归一化了不同变量之间量纲的影响，使得特征之间的关系更加符合实际情况。然而在求解过程中存在协方差矩阵求逆运算，当协方差矩阵为奇异矩阵时会影响到马氏距离计算的数值稳定性，为此要求总体样本数大于样本的维数，以确保协方差矩阵可逆。

定义2.有效观测集

式中：z*是有效观测集；δ是约束上界。

根据定义1与定义2，能够为判断回波是否落入目标的跟踪门内提供一种量化依据。

2.1.2 问题描述

问题1.计算复杂度

随着跟踪目标与有效回波数量的增多，对确认矩阵的拆分次数将会骤增，一般呈指数增长趋势，容易导致组合爆炸问题，影响计算实时性。

问题2.航迹合并现象

如图4所示，三角形为目标，黑点为量测。稀疏工况下，目标之间相距较远，公共量测源来自于杂波的可能性较大；车辆密集工况下，落入公共区域的量测数相对偏多，用来更新目标航迹的组合量测趋于接近，容易产生航迹合并问题，造成目标短暂跟丢的现象。

图4 测量分布特性

2.2 模糊聚类

对于一个航迹或目标来说，所有落入其跟踪波门内的有效量测与目标的关联概率之和为1，构成一个完备事件组，因此可将点迹-航迹关联问题视为一种量测模糊聚类问题，通过求解量测样本与聚类中心的隶属度来间接地计算量测与目标的关联概率。

2.2.1 FCM算法

硬C-均值（hard c-means，HCM）聚类算法的隶属度取值为0与1，聚类速度较快，但其对样本的分类标准是硬性的，聚类结果往往不够准确。模糊C-均值（fuzzy c-means，FCM）聚类算法是基于HCM对样本与聚簇之间的隶属关系进行模糊化，将隶属度取值从HCM算法的二值｛0，1｝扩展到［0，1］区间，使得聚类结果更为合理些。

令量测样本集Z={z1，z2，…，zm}，簇类中心C={c1，c2，…，cn}，模糊隶属度矩阵

定义聚类损失函数为

FCM算法是通过最小化聚类损失函数来实现量测的模糊分类。采用Lagrange乘子法，可得隶属度、聚类中心的迭代式：

其中，迭代终止条件满足|Δci|<ε，ε是约束上界，或者通过限制最大迭代次数来终止。

FCM算法存在的缺陷：①对初始聚类中心敏感；②目标函数的非凸性易致求解极值陷入局部最优，且收敛速度较慢；③未考虑特征的差异性，即有用特征与冗余特征对聚类的贡献值相同。

2.2.2 S-FCM算法

抑制式模糊C-均值（suppressed fuzzy c-means，S-FCM）通过调整隶属度来突出主要因素并抑制次要因素，以增强量测样本对第p类聚类中心的吸引力，减弱对其余类聚类中心的吸引力，从而提高了算法的收敛速度［19］。

对隶属度进行修正：

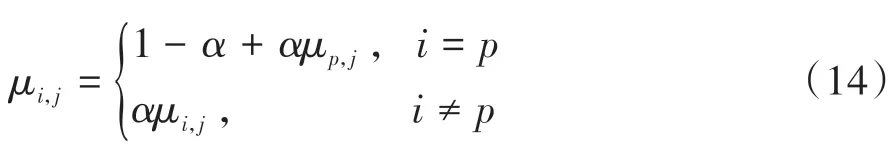
式中：μp，j=max{μi，j}；i∈[1，n]表示量测样本对第p类聚类中心的隶属度是极大的；α是抑制因子，α∈[0，1]，当α=0时，S-FCM退化为HCM，当α=1时，S-FCM即为FCM。

S-FCM算法存在的缺陷：①S-FCM提高了模糊聚类算法的收敛速度，但其聚类效果不及FCM；②当最大隶属度较小时，S-FCM存在过早收敛的隐患。

2.2.3 HS-FCM算法

半抑制式模糊C均值聚类（half suppressed fuzzy c-means，HS-FCM）算法的设计目标是在收敛速度与聚类效果之间寻求平衡。引入抑制门限，对隶属度进一步修正，即

当i=p时，

当i≠p时，

式中β是抑制门限，当β越小时，HS-FCM算法效果越趋近于S-FCM，当β越大时，HS-FCM算法效果越趋近于FCM。建议抑制因子α选取0.5，抑制门限β选取0.5。

2.3 状态滚动估计算法

2.3.1 滚动估计

基于JPDA算法框架，通过互联规则构造统计距离，然后基于模糊数学中的模糊聚类方法，计算各候选量测与观测区域内不同目标的关联概率，再利用概率加权融合方法对各目标状态与协方差进行更新。下一次采样时刻，时域移动一步，并重复上述过程，以实现对各目标状态的滚动估计。一步迭代算式如下。

（a）预测更新

式中：xi(k|k-1)表示对k时刻目标i的状态进行预测；Pi(k|k-1)是对k时刻目标i状态预测的协方差；Q是过程噪声的协方差。

（b）关联概率更新

基于HS-FCM算法得到量测样本的隶属度，对关联概率进行更新。

（c）量测更新

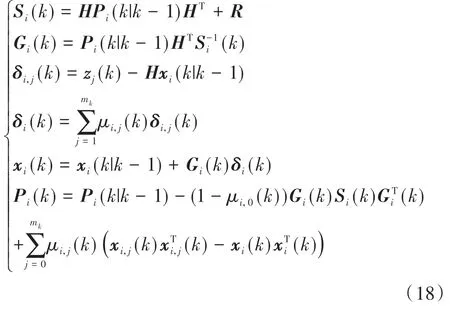
式中：Si(k)是量测协方差；Gi(k)是卡尔曼增益；zj(k)是量测向量；δi，j(k)是量测新息；δi(k)是组合新息；μi，j(k)是k时刻量测j源于目标i的概率；μi，0(k)表示没有量测与目标i关联；xi，j(k)表示基于量测j对目标i的标准卡尔曼滤波估计；xi(k)、Pi(k)分别为k时刻的滤波估计和状态预测的协方差，作为下一步迭代的输入。其中：

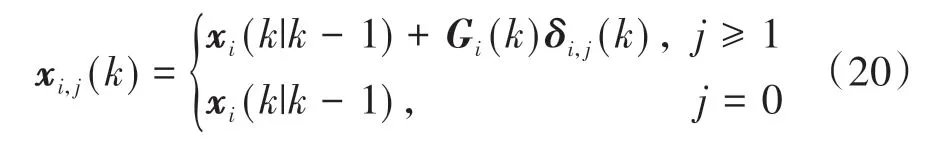
2.3.2 算法改进

为了减少计算量，对式（18）中的状态估计协方差Pi(k)进行优化：

相比式（18）而言，式（21）将无须额外计算各个量测j对目标i的卡尔曼滤波估计xi，j(k)，从而在一定程度上降低了计算复杂度。

车辆密集工况下，虽然量测样本与目标之间的欧式距离较近，但该量测未必源于这个目标，比如总体方差较小时，需要很接近才归为该类，因此建议在车辆密集工况下采用马氏距离代替欧式距离进行聚类。稀疏工况下仍采用欧式距离进行聚类，以期在聚类可靠性与计算复杂度之间寻求平衡。此外，考虑到机动目标的惯性因素，在车辆密集工况下通过合理调整卡尔曼增益对量测更新进行抑制，以克服目标短暂跟丢的问题。

3 仿真验证

试验场景为一段市郊道路工况，通过实车采集雷达与相机数据，再进行离线仿真验证。雷达与相机的主要参数见表1。

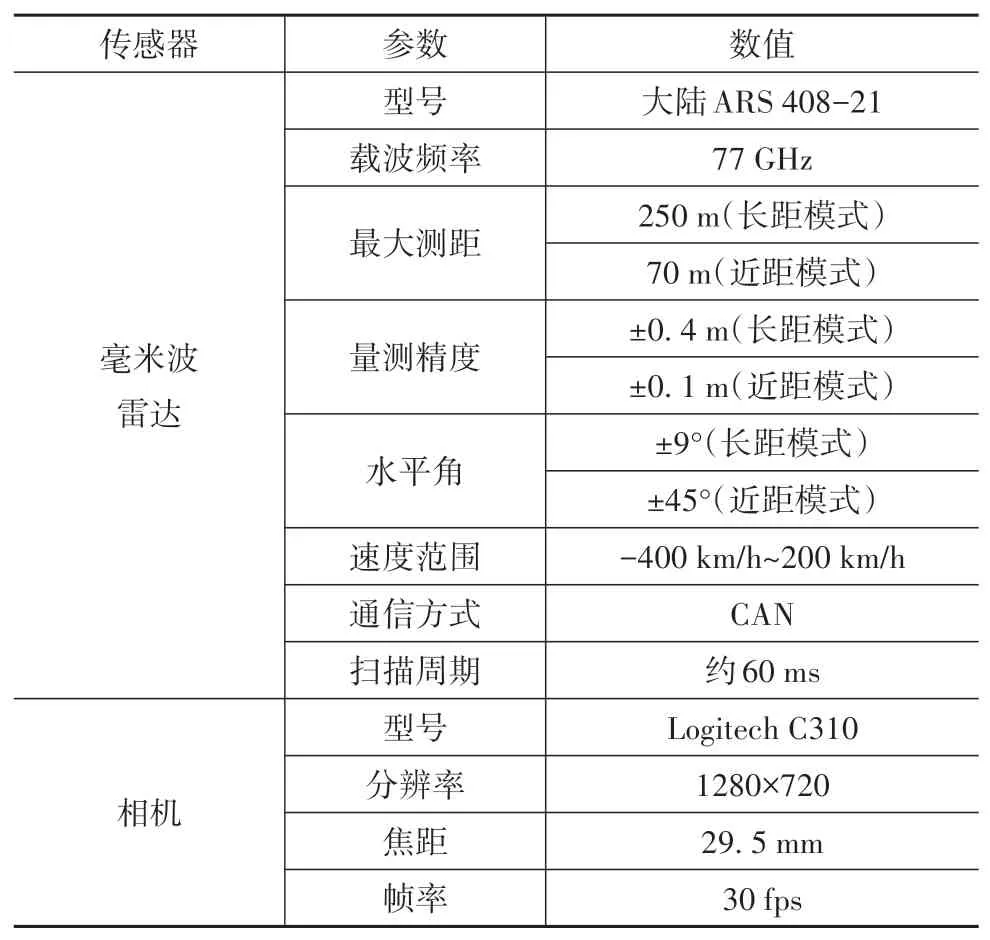
表1 雷达与相机的主要参数

考虑到毫米波雷达较优的纵向测距能力，本文中将雷达的纵向测距数据作为纵向参考，记为REF，将基于YOLO框架的视觉多目标检测算法，记为YOLO估计。

图5 为在一段市郊道路工况下采用YOLO框架对多车道OOI目标车辆进行检测的结果。在车辆检测跟踪过程中，仅标识感兴趣的目标车辆，这是由于OOI目标车辆相对自车来说所构成的追尾威胁较为明显。

图5 多车道OOI目标车辆检测结果

图6 为主车道OOI目标车辆纵向运动估计的对比情况。

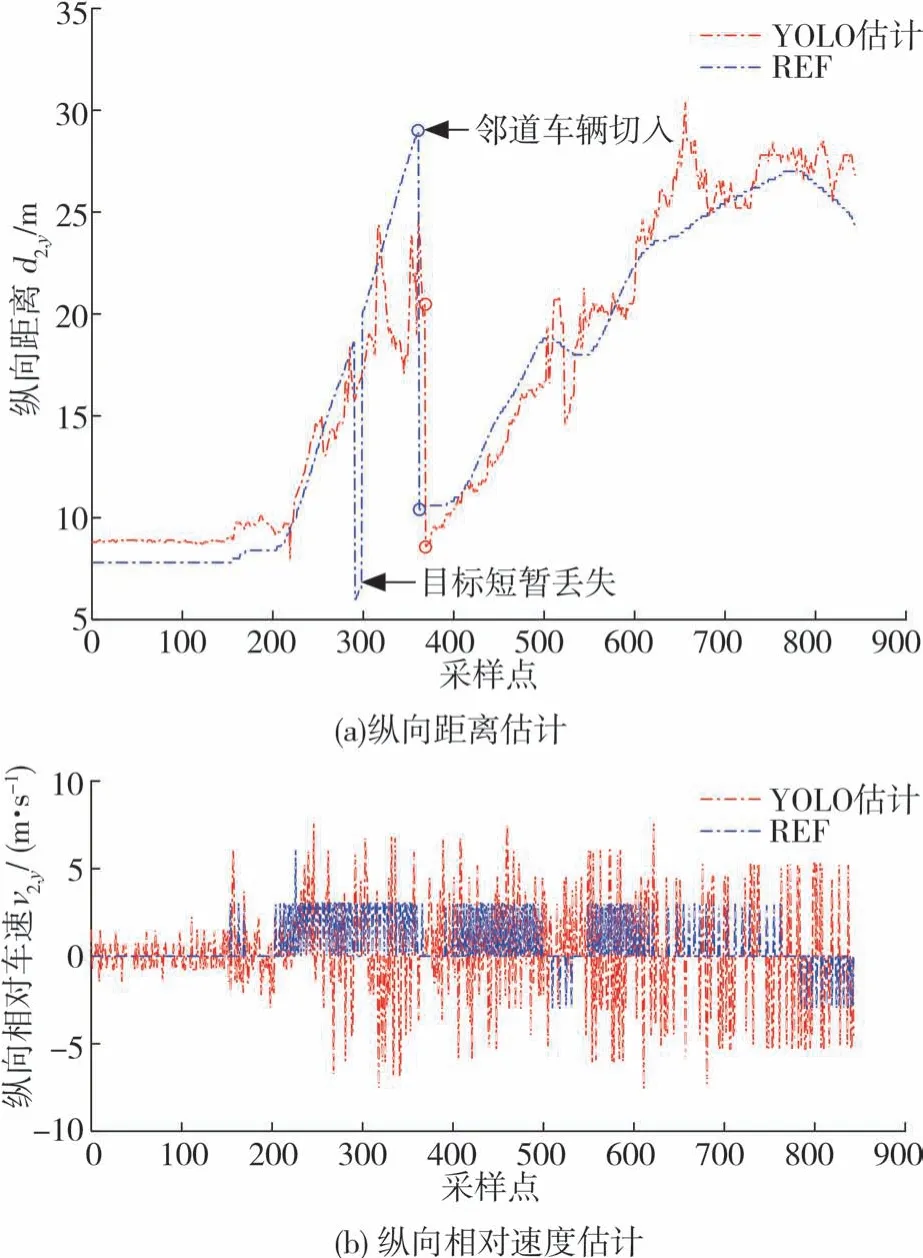
图6 主车道OOI目标车辆纵向运动估计对比

由图可见，在接近第300个采样点时刻，雷达采样点出现目标短暂丢失现象，这是由于雷达可能探测到邻近车辆，而妨碍了对前方车辆的精准跟踪。在300-400采样区间，由于邻道车辆的切入，更新了当前跟踪的OOI目标车辆，进而导致跟踪轨迹发生了陡变。

图7 为基于改良JPDA滤波的主车道OOI目标车辆纵向运动估计的对比情况。在车辆密集工况下，通过调整卡尔曼增益对量测更新进行抑制，以增加预测的置信度，基于改良JPDA滤波后的雷达估计能够较好地解决图6中雷达估计出现的目标短暂丢失问题。此外，在200-800采样区间，基于改良JPDA滤波后的YOLO估计曲线抖动较小，纵向距离的均方根误差由0.118 3降为0.070 7，较好地抑制了视觉量测误差，从而在一定程度上增强了视觉跟踪性能。

图7 改良后的主车道OOI目标车辆纵向运动估计对比

图8 为基于改良JPDA滤波与标准JPDA滤波估计的对比情况。两者滤波后的轨迹都更接近于雷达的状态估计，也进一步表明JPDA滤波对量测抖动有较好的抑制效果。此外，改良JPDA滤波避免了标准JPDA滤波过程中确认矩阵复杂的拆分组合环节。

图8 改良JPDA与标准JPDA滤波估计对比

图9 为主车道OOI目标车辆横向运动估计的对比情况。在200-800采样区间，雷达估计的横向距离的均方根误差为0.023 3，YOLO估计的横向距离的均方根误差为0.010 2。相对来说，雷达横向跟踪性能易受扰动因素影响。

图9 主车道OOI目标车辆横向运动估计对比

图10 与图11分别为左右车道OOI目标车辆运动估计的对比情况。整体上来看，基于改良JPDA的滤波算法能够较好地实现多目标跟踪，且视觉的横向跟踪效果较优，雷达的纵向跟踪效果较佳。

图10 左车道OOI目标车辆运动估计对比

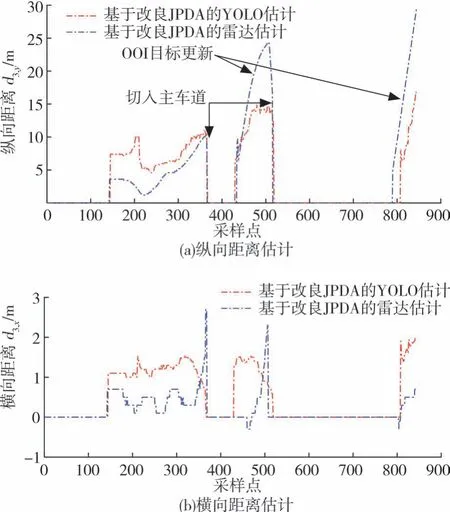
图11 右车道OOI目标车辆运动估计对比

4 结论

为了提高密集杂波环境下多目标数据关联的可靠性与实时性，本文中设计了一种多目标车辆跟踪算法，主要结论如下。

（1）基于模糊理论将点迹-航迹关联问题转换成量测模糊聚类问题，利用模糊隶属度来代替JPDA算法中不确定性量测与各目标的关联概率，能够一定程度上降低计算复杂度。

（2）在车辆密集工况下通过合理调整卡尔曼增益对量测更新进行抑制，能够较好地解决目标短暂跟丢的问题。

（3）在调试过程中发现，合理选取HS-FCM算法中的抑制因子与抑制门限以改善聚类效果，能够一定程度上避免航迹合并现象，后续将进一步深入对该问题的研究。