基于EGO加点策略的动力电池包多目标优化*

王普毅，白影春，林程，武振江，王保华

（1.北京理工大学，电动车辆国家工程实验室，北京100081；2.湖南大学，汽车车身先进设计制造国家重点实验室，长沙410082；3.西北机电工程研究所，咸阳712099；4.中汽研（天津）汽车工程研究院有限公司，天津300300）

前言

动力电池包是电动汽车动力系统的重要组成部分，在确保结构承载能力和机械防护能力的前提下，开展针对电池箱的轻量化设计可提升动力电池能量密度进而延长电动汽车续驶里程。

国内外研究人员围绕电池箱结构轻量化和结构安全做了大量的研究工作。赵红伟等［1］采用拓扑优化方法实现了电池箱的轻量化设计。陈静等［2］和Chen等［3］采用轻质材料实现了电池箱的轻量化和强度设计。孙小卯［4］根据静力学、模态和疲劳分析结果，对电池箱进行改进设计，提高了其动、静态性能和疲劳寿命。Choi等［5］采用热塑性纤维复合材料研制了一种轻量化电池组壳体，并完成了冲击振动和耐久性分析；朱新春［6］完成了极限工况下电池箱的轻量化和形貌优化。兰凤崇等［7］采用拓扑优化、综合多项性能和质量的多目标优化，提升了电池箱动、静态特性和轻量化水平。李志杰等［8］运用复杂系统安全理论结合电动汽车实际工况，提出机械外力下基于整体精细化模型可量化、层次化的动力电池包系统安全性评价方法。黄培鑫等［9］建立了动力电池包结构及其内部精细化模型和分析方法，兰凤崇等［10］在此基础上分析了电连接结构在稳态随机振动和瞬态冲击下的损伤和接触可靠性。尽管以上研究工作为电池箱轻量化和安全性设计提出了方法和思路，但针对基于代理模型的动力电池包结构多目标优化和通过动态更新代理模型以实现高效全局优化方面的研究仍较少。

在实现高效全局优化方面，Jones等［11］提出了单目标优化问题的高效全局优化（efficient global optimization，EGO）策略，优化算法通过求解期望改进（expected improvement，EI）函数的最大值来确定EI点，进而用于模型更新。Koji等［12］通过超体积指标来寻求Pareto前沿（Pareto front，PF）EI点，但超体积指标求解复杂、耗时，且存在较大计算误差。Yang等［13］在粒子群优化（particle swarm optimization，PSO）算法中增加辅助代理模型，采用EGO策略寻找优势粒子和更新非劣解，在高效求解单目标全局优化方面取得了较好效果。Lin等［14］提出了一种基于代理模型的多目标优化智能抽样方法，该方法在当前优化解最大化最小距离点、极端采样点、最近边界点之间进行权衡，进而获得新的采样点并用于代理模型的更新，但确定加权系数过于依赖经验。以上研究在高效全局寻优方面为动力电池包结构的多目标优化提供了思路，然而针对复杂结构的高维多目标优化设计问题，有必要在优化过程中降低计算复杂度和难度，实现快速求解。

本文中针对动力电池包结构多目标优化问题，在分析初始设计的基础上，提出多目标优化模型和优化流程。根据优化流程，基于试验设计和Pareto法则开展变量影响分析以缩减优化参数；基于样本点构建的优化目标KRG模型，采用多目标粒子群优化（multi⁃objective particle swarm optimization，MO⁃PSO）算法求解多目标优化问题；以过程优化解为插值点构造EI采样函数，采用EGO加点策略求解新增样本点，进而更新代理模型。最后，使用测试函数对优化方法进行验证，并将其用于随机振动下的电池包结构的多目标优化。

1 动力电池包初始设计

1.1 某型电池包初始设计参数

某型动力电池包主要由电池箱（即电池包的壳体）、电池模组和电池管理系统组成，初始总质量为549.5 kg。电池箱作为电池结构的主要组成部分，初始设计质量为90.55 kg，其组成零件材料采用高强钢，初始设计参数和材料性能如表1所示。表1中，支板包含前、后支板；横梁包含前、后、左、右和中横梁；纵梁包含前、后、第一、第二、第三和第四纵梁；托架包含左、右托架；压板包含上、下压板。

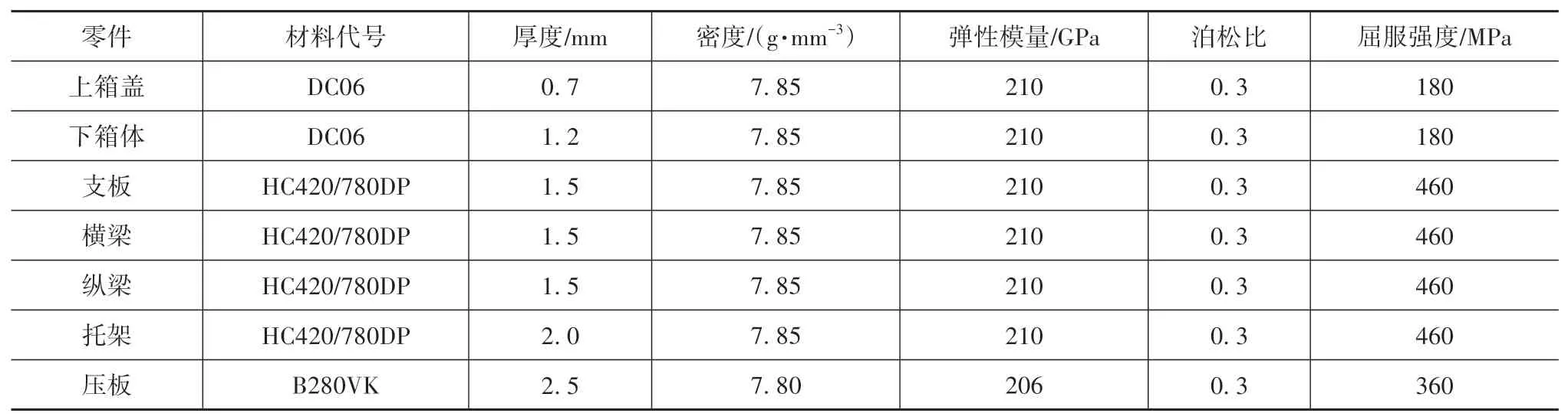
表1 电池箱主要零件初始几何参数与材料特性

1.2 电池包初始设计模态分析

电池包结构阻尼小，通常被当做线性结构来分析［9，15］，其简化自由振动动力学方程为

式中：M和K分别为系统质量矩阵和刚度矩阵；ẍ(t)、x(t)分别为加速度和位移向量。

考虑约束模态引入的附加刚度K'，由式（1）可得约束模态频率ω的方程为

如图1所示，约束电池包托架6个自由度，利用Lanczos法获取前6阶模态。分析结果显示，电池包初始1阶模态频率值达到了31.52 Hz，高于常见车辆激振频率范围（17-25 Hz）。

图1 电池包有限元模型及约束位置

2 优化模型和优化流程

2.1 优化模型的建立

提高电池包1阶模态频率可使其远离低频共振区，降低结构部分质量可提升电池能量密度。因此，电池包多目标优化模型可表示为

式中：f1（x）和f2（x）分别为电池包质量和1阶模态频率；x=［x1，…，xk，…，xm］表示电池箱零件厚度；xl和xu分别为设计变量上、下边界。

2.2 优化流程

为解决上述优化问题，本文中提出了基于EGO加点策略的多目标粒子群优化（EGO-MOPSO）流程，如图2所示。首先根据分析要求定义初始条件。其次，通过多变量试验设计样本和多变量影响分析，选出对目标贡献较大的变量作为优化对象。然后，以上述条件为基础生成新试验样本，构建优化目标的KRG模型。使用MOPSO算法求解优化问题，并采用过程优化解构建EI采样函数，利用EGO加点策略求解EI采样点，进而获取真实填充样本，用于更新代理模型。最后，若满足条件则输出结果。为防止样本重合而导致KRG模型构建失败，采用过滤策略删除重叠样本。

图2 电池包结构优化流程

3 基于EGO加点策略的多目标优化

3.1 试验设计和优化设计变量的选取

以电池箱19个零件厚度作为设计变量（x1~x19），以电池包的总质量和1阶模态频率作为响应，通过拉丁超立方抽样完成试验设计，并利用多变量线性影响分析和Pareto法则分析变量对响应的影响，结果如图3和图4所示。图中分别列出了对电池包的总质量和1阶模态频率影响较大的7个设计变量。为充分缩减优化规模，并优先考虑变量对电池包模态性能的影响，最终选择电池箱的上箱盖、下箱体、后支板、前支板、第二纵梁、左横梁和右横梁等7个零件（图5）的厚度值作为设计变量，优化设计的取值范围如表2所示。最后，以此为基础再次开展试验设计，获得用于后续优化所需的试验样本。

表2 设计变量取值范围及初始值 mm

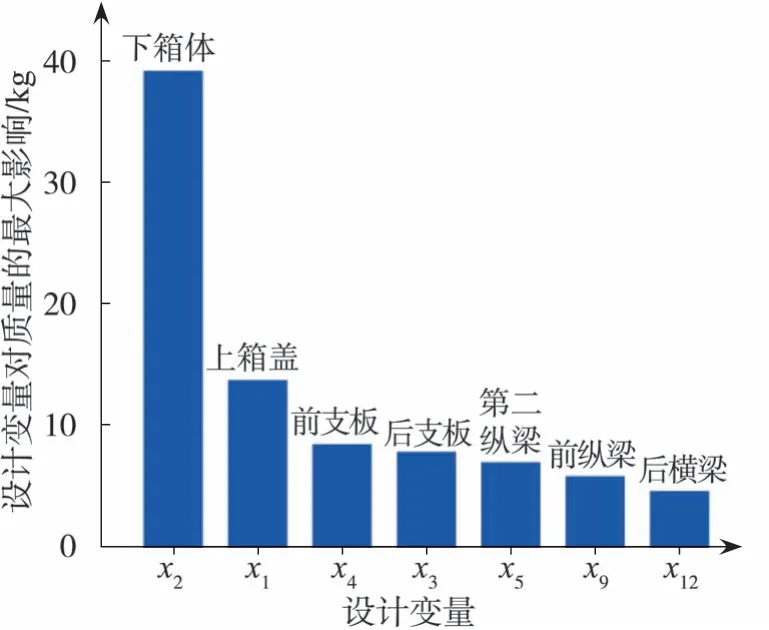
图3 设计变量对电池包质量的影响

图4 设计变量对电池包1阶固有频率的影响

图5 电池箱的优化零件

3.2 构建优化目标的代理模型

KRG模型因具有无偏估计特性、可选相关函数范围广且灵活，而得到广泛应用［16-17］。本文构建优化目标所用的KRG代理模型可表示为

式中：G（x）为全局近似模型；z（x）为局部偏差，其均值为零、方差为σ2、协方差非零。

3.3 多目标粒子群优化

采用MOPSO算法，可调参数少，无需梯度信息，仅通过粒子速度和位置的不断进化而得到最优解，算法易实现且效率高［18］。

由式（3）多目标参数优化问题可描述为

式中：Ff（x）为粒子适应度函数，即目标函数值；Rm为设计变量域，m=7；x=［x1，…，x7］。

另外，在粒子群优化算法中，第i个粒子的速度更新策略为

式中：vi(t-1)和vi(t)分别为更新前后粒子的速度；w为惯性权重系数；wd为惯性权重阻尼率；xi为粒子当前位置为当前粒子局部最优位置为当前粒子全局最优位置；C1为局部学习因子；C2为全局学习因子。

相应地，第i个粒子的位置更新策略为

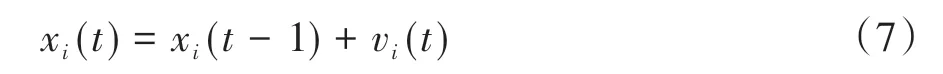
为避免算法过早收敛，算法中采用变异策略来更新粒子速度和位置，以尽量避免局部最优。变异函数系数为

式中：pm为变异系数；t为当前迭代数；N为最大迭代数；mu为变异率。

MOPSO算法设置如下：种群规模取100，最大迭代数取80，权重系数取0.5，个体学习因子取1，全局学习因子取2，惯性权重阻尼率取0.99，外部存档网格数取10，变异率取0.1。

3.4 基于EGO加点策略的代理模型更新方法

一次性的代理模型对于近似复杂结构高维优化问题往往精度不理想。为此，基于EGO加点策略，通过有针对性地增加样本点来快速开发设计域和提高模型精度［11，13］。

EGO以KRG为代理模型，点x处的预测值f̂(x)~N(μ，s2)，其均值μ和方差s2由当前模型确定，以EI函数作为填充采样准则［11］，即

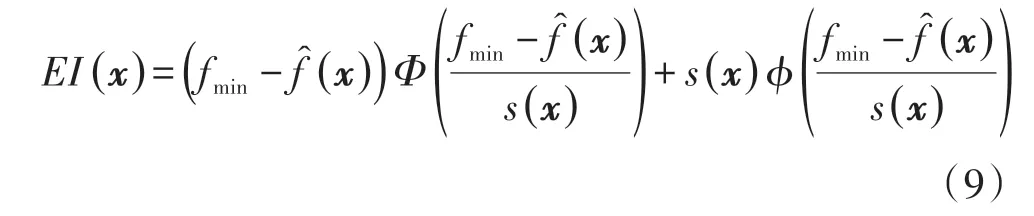
式中：fmin为当前最优响应；f̂(x)和s（x）分别为当前模型预测响应和标准差；Φ（·）和φ（·）分别为标准正态概率分布和概率密度函数。EI（x）值越大，表明在x处的近似精度就越差，设计空间应在此处增加样本点。代理模型更新流程如下。

输出：第k次更新后的样本Sk。

步骤1：开始。

步骤2：若k>n且σδ≤3%，转步骤9。

步骤3：更新代理模型，获得mass_new_KRG和freq._new_KRG。

步骤4：利用MOPSO获得Pareto解和目标函数值，即（xk，f1，k）和（xk，f2，k）。

步骤5：以（xk，f1，k）和（xk，f2，k）为插值点集，构建mass_Pareto_KRG和freq._Pareto_KRG代理 模型、mass_EI和freq._EI函数。

步骤6：求解EI点mass_xnew和freq._xnew、EI点响应mass_xnew_f1，2和freq._xnew_f1，2。产生新样本点。

步骤7：新样本点过滤。若全部为重叠点，转步骤4。

步骤8：样本更新为Sk+1，k=k+1。转步骤2。

步骤9：输出优化解。

步骤10：结束。

该流程始于第一次获得更新样本之后。

步骤2是对填充采样和样本更新是否结束的判断。若满足要求，转步骤9，输出优化解。否则，在步骤3构建新质量模型mass_new_KRG和1阶模态频率模型freq._new_KRG。

步骤4采用MOPSO算法求解优化问题，获得Pareto解和目标值，组成插值点集（xk，f1，k）和（xk，f2，k）。

步骤5和步骤6构建基于电池包质量和1阶模态频率KRG模型，即mass_Pareto_KRG和freq._Pareto_KRG。由式（9）构造质量和1阶模态频率的EI采样函数，即mass_EI和freq._EI，期望函数最大的点即为两个优化目标的EI采样点，即mass_xnew和freq._xnew。进而获得新样本点（mass_xnew，mass_xnew_f1，2）和（freq._xnew，freq._xnew_f1，2）。

步骤7对新样本点进行过滤。新试验点若满足式（10），则判定该点为重叠试验点。

max{|xi，j-xnew|，|f1，j-f1，new|，|f2，j-f2，new|}≤ε（10）式中：xi，j、f1，i和f2，i分别表示已有样本中第i个试验点的第j个变量、质量和1阶模态频率，i=1，…，N，j=1，…，7；xnew，j、f1，new和f2，new分别表示新试验点的第j个变量、质量和1阶模态频率响应；ε为给定阈值，文中取为10-3。若填充采样点均为重叠试验点，则转入步骤4。

在步骤8中，将获取新试验点填充到原样本Sk中，得到新样本Sk+1。由算法流程可知，只需至少存在一个不重叠的填充采样点，便可实施样本更新。回到步骤2中，若不满足条件，则对代理模型进行更新。

3.5 优化终止条件

将同时满足不少于试验样本更新次数n和不大于新增试验点预测值相对误差的标准差σδ作为收敛条件，其中n=10，σδ=3%。

4 优化结果分析与讨论

使用测试函数ZDT1和ZDT3对EGO⁃MOPSO进行验证［19-20］，并与MOPSO对比。随后用于电池包结构多目标优化。优化计算均在同一条件下运行。其中，硬件：CPU⁃Intel Core i5⁃7360U，2.3 GHz，内存8 GB；软件：Win10（64位）操作系统；MATLAB（R2020a）。

4.1 优化算法数值测试与验证对比

4.1.1 测试1

ZDT1函数为

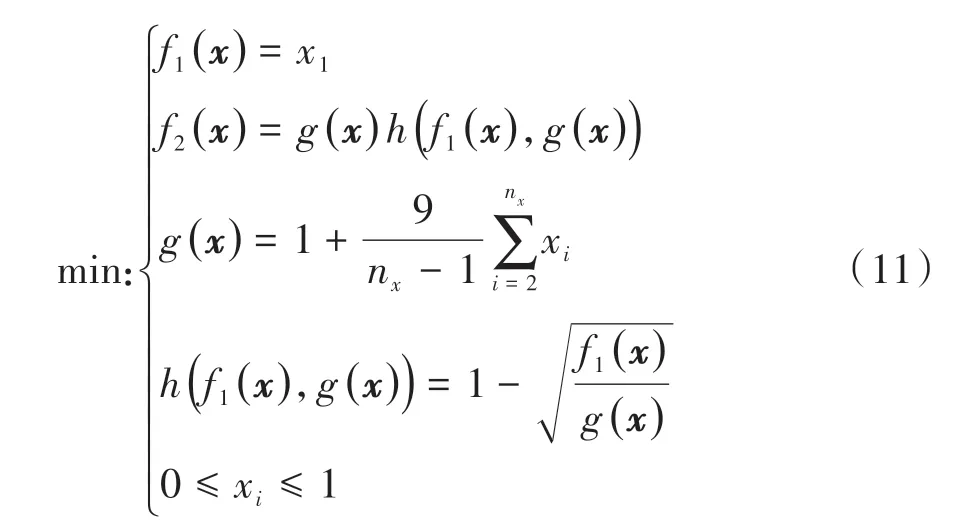
式中nx为变量个数，本例中取2。

初始样本数取100，MOPSO种群规模取100，最大迭代数取20，非劣解存储容量取30。经过3次加点，结果如图6所示。

图6 使用ZDT1函数验证时的PF对比

4.1.2 测试2

ZDT3函数为

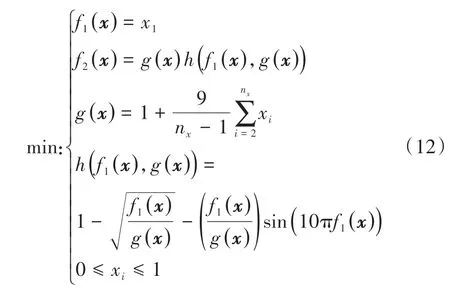
式中nx为变量个数，本例中取2。

初始样本数取180，MOPSO种群规模取100，最大迭代数取40，非劣解存储容量取50。经过4次加点，结果如图7所示。

图7 使用ZDT3函数验证时的PF对比

从图6和图7看出：对于以ZDT1函数为代表、PF呈连续分布的优化问题，通过加点3次便能使优化结果快速收敛至真实PF附近；对于以ZDT3函数为代表、PF呈断续分布的优化问题，在较少的初始样本和迭代次数条件下，也能通过加点4次较快地靠近真实PF。

4.1.3 收敛性能和PF分布均匀性评价

多目标优化算法收敛性能、PF分布均匀性的常用评价指标［19］为反向世代距离（inverted generational distance，IGD）。IGD值越小，表明算法越好。沿用测试函数优化求解设置，随机生成3组不同的初始样本，每组样本分别使用MOPSO和EGO⁃MOPSO进行优化求解10次。计算平均IGD和平均耗时；ZDT1和ZDT3函数分别按3次和4次加点验证设计。

两种算法的平均IGD和平均耗时如表3和表4所示。结果显示，EGO⁃MOPSO的IGD值明显占优，但求解耗时稍长。经分析，多消耗的求解时间主要花在EI点计算模块，但这部分时间占比较小。在工程应用中，为寻求更高质量的IGD，特别是在提高计算机硬件性能的情况下，多消耗的这点求解时间是可接受的。

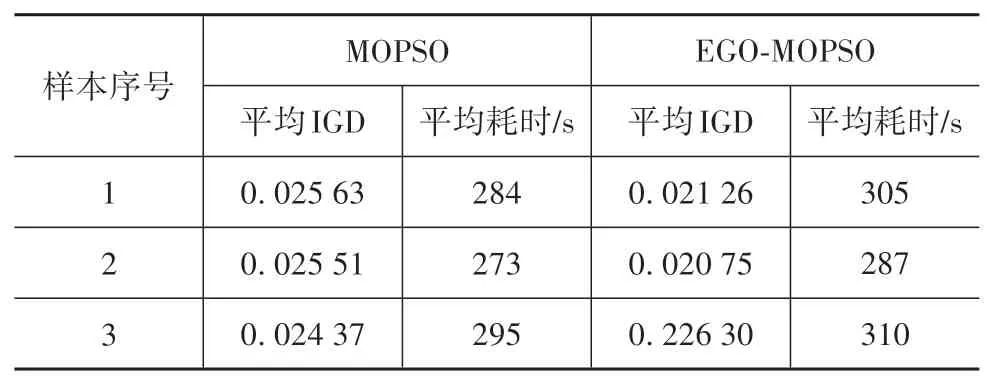
表3 两种算法求解ZDT1的平均IGD和平均耗时

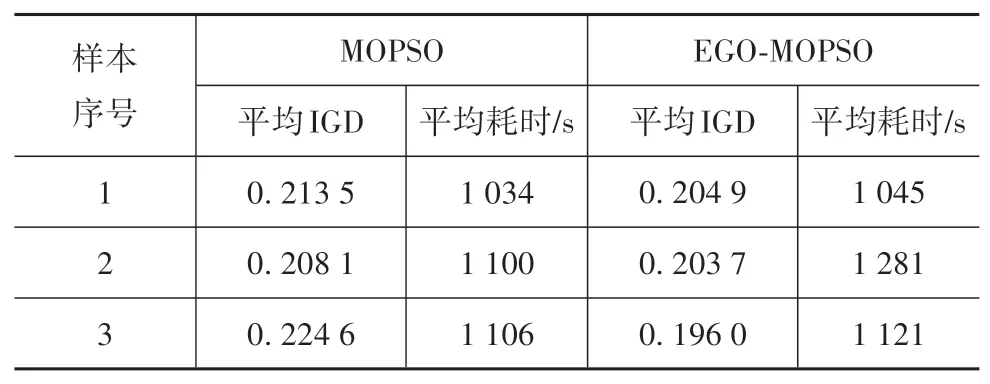
表4 两种算法求解ZDT3的平均IGD和平均耗时

4.2 电池包结构多目标优化结果分析

经数值验证有效后，将所提出的优化方法应用于某电池包结构多目标优化。

4.2.1 计算资源消耗

选取256个初始试验点，样本最大更新次数设置为10。优化过程一共产生12个EI采样点，包括两个质量采样点和10个1阶模态频率采样点，计算总耗时约230 min。其中，EI采样点的物理响应须调用有限元分析，耗时较长。

4.2.2 EGO加点策略效果与收敛性分析讨论

表5 为优化前后的代理模型精度对比。由表可见，使用该方法后，目标响应代理模型预测精度有较明显的提高。决定系数分别增加到0.979 9和0.913 1，增加了2.4%和2.8%；均方根误差分别减小到0.98 kg和0.14 Hz，减小了29.5%和6.7%，说明所用方法可有效提高代理模型精度。

表5 优化前后的代理模型精度

如图8所示，使质量最小的EI点处，质量和1阶模态频率值仅在第5个试验样本循环中出现小幅波动，其余均相同。在EI点处的响应预测值也达到较高精度，相对误差小且稳定；质量和1阶模态频率预测相对误差标准差分别为0.001 3%和0.124%。

图8 质量最优时EI点的预测相对误差

如图9所示，使1阶模态频率最大的EI点处的质量和频率预测值在小幅波动后迅速收窄。在EI点处的响应预测值也达到较高精度，相对误差较小且迅速趋于稳定；质量和1阶模态频率预测相对误差的标准差分别为0.393%和1.05%。

图9 1阶模态频率最优时EI点的预测相对误差

图10 给出了试验样本更新过程中第2、4、6、8、10次多目标优化的PF。图中显示，质量小于545 kg时，几次迭代后的PF几乎重合，这主要是由于使质量最小的期望改进很快趋于一致的缘故。在质量大于545 kg、1阶模态频率大于32 Hz后，PF出现了小幅震荡，这主要是由于不断新增了使1阶频率最大的期望改进样本点的缘故。但随着更新次数的增加，1阶频率最大的期望改进也很快接近一致，因此PF点也趋于平稳、均匀，并向第10次试验样本更新后的PF靠拢收敛。

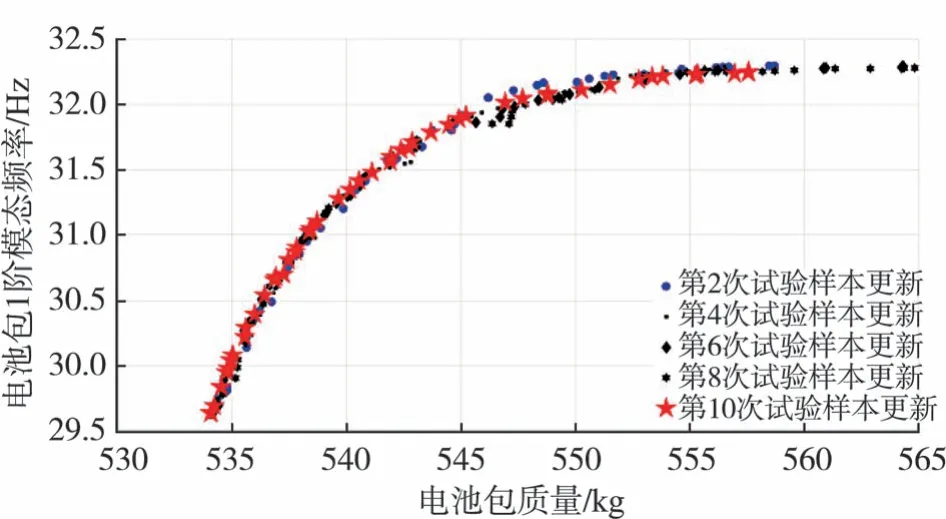
图10 多目标优化迭代过程中的PF

以上分析结果表明，本文所提出的优化方法能够高效完成质量和1阶模态频率的设计域全局寻优和填充采样。利用新试验点更新代理模型，提高了模型精度。同时，随着MOPSO的循环寻优，多目标优化解也逐渐趋向稳定。

4.2.3 多目标优化结果的分析与讨论

如图11所示，“MOPSO”代表加点之前的PF；“EGO⁃MOPSO”表示满足收敛条件的PF；矩形框内的点是优于初始设计的优化值。结合验证结果可以看出，使用EGO加点策略后，在不断改善代理模型精度的同时，PF点逐渐趋于均匀和稳定。

以优于初始设计值为标准，选择图11中矩形框内“EGO⁃MOPSO”PF上的13个点作为初选目标值和优化解进行数据圆整，得到表6中的5组候选设计变量组合。

图11 多目标优化PF及初始设计对比

表6 圆整后的优化设计变量值 mm

4.3 随机振动工况下的优化解

根据“电动汽车用动力蓄电池安全要求”中规定的电池包随机振动测试要求，选取表6中的5组优化解，按表7中载荷要求进行电池包结构强度分析。为高效完成分析，选择工况最恶劣的Z向进行载荷加载，计算结果如表8所示。

表7 随机振动载荷加载要求

表8 中第4组和第5组解在结构应力方面表现较好，且具有相同的最大结构应力。选择质量较小的第4组解进行结构强度分析，电池包结构应力云图如图12所示。

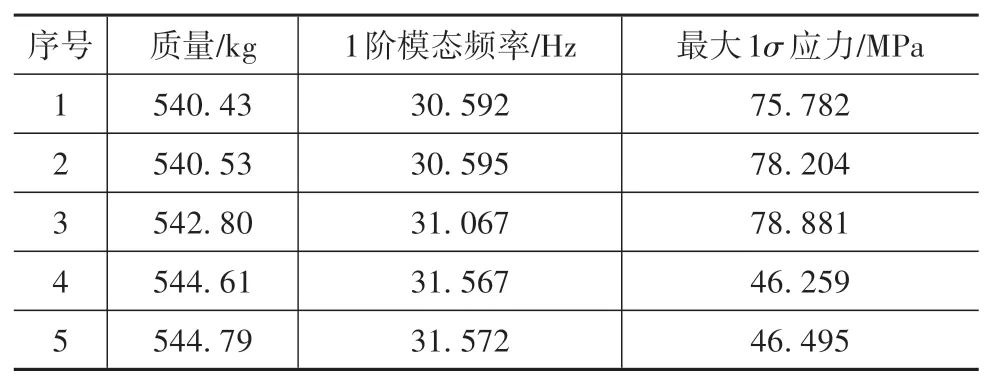
表8 随机振动工况下（Z轴）的优化解

图12 第4组优化解对应的电池包结构应力云图

图12 中电池包结构整体应力水平较低，最大应力位于上箱盖中后部。根据Steinberg应力三区间法理 论［21］，第4组 解 对 应 的 结 构 最 大3σ应 力 为138.777 MPa，小于材料屈服强度（180 MPa），可满足随机振动下结构强度的要求。

5 结论

（1）以电池包为研究对象，提出了基于EGO加点策略的多目标粒子群优化方法。数值验证和优化分析结果表明，该方法实现了代理模型的高效更新，具有较好的收敛性和多目标优化值分布均匀性。

（2）基于EGO⁃MOPSO方法开展了电池包结构多目标优化和随机振动分析。结果表明，随机振动下的优化结构最大3σ应力为138.777 MPa，低于材料屈服强度，满足强度安全要求；结构最大可减质量4.89 kg。

（3）通过测试函数和电池包结构多目标优化验证，表明所提出的方法有效可行，可为复杂结构的多目标优化提供重要的参考。