基于机器学习算法的煤矿汽车机械设备故障诊断模型

李玉吉，曹旭辉，王江宏，赵 欣

(陕西国防工业职业技术学院，陕西 西安 710300)

煤炭是我国当前较为重要的资源之一[1]，能够顺利进行煤矿生产，是现阶段社会中所要研究的关键方向[2]。顺利运行的煤矿汽车机械设备能够使为煤炭生产提供重要保障，并且是煤炭企业的核心技术[3]。在煤炭生产环节，生产环境较为恶劣[4]，煤矿汽车机械设备的安全性能也时常无法保障，因此，通过有效方式保障煤矿汽车机械设备的顺利运行[5-6]，能够顺利提升煤炭生产的质量。许多学者对检测故障问题进行研究，如徐青青等[7]研究诊断煤矿机械轴承故障方法，刘永亮[8]研究诊断煤矿机械齿轮箱故障方法，但当故障发生率较高时，依然存在泛化错误等问题，并且随着故障的增加还会发生检测精度降低等事件。低秩鉴别投影算法能够有效判别结构，还能有效进行泛化，采用低秩鉴别投影算法，能够有效提取故障特征[9]。神经网络方法能够基于人脑的思维想法，诊断噪声较强等存在问题的信息[10-11]。因此本文设计基于机器学习算法的煤矿汽车机械设备故障诊断模型，通过低秩鉴别投影算法提取故障特征，再根据特征，采用ART神经网络学习算法进行故障诊断。

1 故障诊断模型

1.1 特征提取

采用基于低秩鉴别投影算法，提取煤矿汽车机械设备故障特征，该算法判别结构描述功能较强，并且还拥有全局资源描述功能，可以改善新样本的提取速度[12]，获取明显的投影矩阵。

1.1.1 低秩鉴别投影算法

该算法的主要过程是：首先获取低秩表示模型的系数矩阵L，并将其划分为噪声、类内、类间，并使类间与类内散度分别保持够大以及够小，之后赋予经线性投影资源恒定的低秩结构，并维持较强的数据低维空间聚类能力[13]。通过L表示系数矩阵，由式(1)描述低秩表示模型：

(1)

式中，λ>0；E为噪声；E2，1为l2，1范数，其定义了噪声的规范。

(2)

若低秩矩阵经式(3)变化后未发生改变：

y=PT

(3)

式中，P为投影矩阵。

yi，j的计算公式为：

(4)

(5)

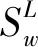
同时，依据式(6)表示类间散度：

(6)

为达到资源划分合理，同时投影后噪声保持最低，所以需要最小化PTei，j的范数，计算公式为：

(7)

通过式(8)判断最优投影的过程：

(8)

式中，类内与噪声散度被r所维持。

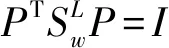
1.1.2 低秩鉴别投影算法步骤

(1)以数据集X为基础，定义其为c类，求出最优相似矩阵L，对L的获取采用非精确增广拉格朗日乘子法。

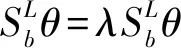
1.2 ART神经网络学习算法改进

ART神经网络是由两层神经元构成，分别是比较层与识别层，其通过识别层中的一个单一神经元进行类别判决。并且能够在线学习，自适应性较好。通过什么方式解决逐步削弱神经网络的学习率和邻域，对于学习的聚类精度和收敛速度非常重要，因此通过墨西哥草帽函数改进ART神经网络学习算法。通过逐渐削弱幂函数，可以提升收敛效果，提供较好的聚类条件，因此，通过式(9)削弱学习速率η：

(9)

式中，a1通常值为0.05。

邻域函数通过墨西哥草帽函数描述，在邻域中，获胜神经元和内神经元i的间距与侧反馈的强度存在关系，具体为：

(10)

式中，rij为竞争层神经元的间距；δ(t)为邻域的可用水平方向的长度。rij的计算公式为：

rij=‖wi-wj‖

(11)

式中，wi和wj为关联竞争性神经元的权值，并通过幂函数逐步削弱，具体为：

(12)

式中，a2通常取0.5。因此得出调整权值方式为：

(13)

经迭代后，计算过程趋弱了邻域区域外划分故障的作用，提升了邻域内划分类的作用，并通过非线性函数，提升收敛效果。由式(14)、式(15)计算神经网络识别层的发送：

(14)

(15)

式中，ξ为神经网络的门限值，在开始过程中通常取值0.6，ξ∈[0，1]，而操作过程中与操作完成时期取值0.8，通过在0～1区域内逐次0.05添加ξ的值，以改善诊断效果，研究分类程度，使ξ每个周期的值都能被监测到，最终获取矢量输出。

1.3 改进ART神经网络的建立

(1)学习阶段1。①获取输入最优投影矩阵的列向量；②开始运行ART网络权值，向其中导入最优投影矩阵的列向量；③与竞争层相关联的神经元，在获取某一类样本时被启动，之后样本输出值高于其他所有值，各类竞争神经元与神经元的间隔由欧氏距离描述；④估量邻域函数值和调整权系数；⑤逐步削弱学习率和邻域水平方向的长度；⑥循环操作步骤③，一直到总体样本都经过操作；⑦迭代次数增加，当迭代次数大于最大迭代次数情况下完成。

(2)学习阶段2。循环操作步骤②—⑥，T2=200，η0=0.04，δ0=1，ξ=0.8，逐步削弱学习率和邻域水平方向的长度，向所选样本添加网络，选取另一组最优投影矩阵的列向量提供网络输入，并折返，在样本平稳地与兴奋神经元链接时结束。T=t+1，在t>T2情况下完成操作。将神经元的相关权系数发送并保存，即完成ART神经网络的操作过程，最终实现煤矿汽车机械设备故障诊断。

2 验证性实验

将本文模型应用于某煤矿企业中，分析该企业煤矿汽车设备的故障发生情况。并选取文献[7]一种煤矿汽车机械轴承故障诊断模型、文献[8] 煤矿汽车机械齿轮箱故障诊断模型作为本文模型的对比模型，通过以下实验验证故障诊断效果。随机选取25个故障进行分析，分析不同诊断模型的故障识别能力，分析结果如图1所示。根据图1可知，随着故障样本数量的提升，3种模型的故障识别能力逐渐下降，文献[7]模型的故障识别能力始终保持最低，并且随着故障数量增加识别率迅速下降，而文献[8]模型的故障识别率要高于文献[7]模型，但依然低于本文模型，本文模型在故障数量增加时，故障识别率保持缓慢下降的形式，从最高96%逐渐降低至87%，并且一直高于其他2种模型，本文模型的故障识别效果较好。

图1 故障识别能力Fig.1 Fault recognition capability

对故障诊断模型进行分析，选取所存在的10个故障，分析3种模型故障诊断的泛化性能，分析结果如图2所示。根据图2可知，随着故障的提升，不同模型设备故障诊断的泛化错误逐渐较高，文献[7]模型的泛化错误最高要达到4.88%，而文献[6]模型的泛化错误最高也要达到4.71%，并且2种模型的泛化错误都要同时高于本文模型，因此，本文模型在设备故障诊断过程中，存在较少的泛化错误。

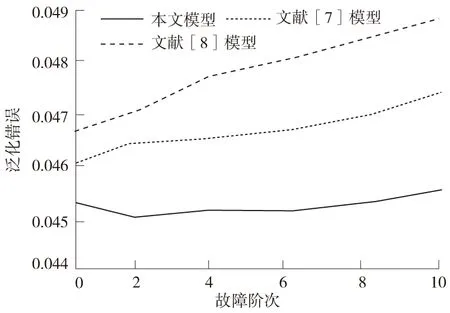
图2 不同模型的泛化错误Fig.2 Generalization error of different models

测试数据选取4 000个正常设备数据，5 000个异常样本，分析训练后不同模型的ROC曲线对比，分析结果如图3所示。根据图3可知，在误检率为0.03时，3种模型的诊断进度较为接近，但误检率达到0.15时，3种模型出现较大差距，并且本文模型的诊断精度始终高于另外2种模型，因此，本文模型具有较好的泛化能力。

图3 不同模型的ROC曲线Fig.3 ROC curves of different models

对比3种模型，分析在信噪比不同的情况下故障诊断的程度，分析结果如图4所示。根据图4可知，由于信噪比逐渐下降，不同模型的故障诊断准确率也随之降低，文献[8]模型的诊断准确率在信噪比为5、0、-5、-10 dB时，要高于文献[7]模型，但信噪比为20、15、10 dB的情况下，文献[8]模型诊断准确率低于文献[7]模型，并且文献[8]模型的最高故障诊断准确率为80%，文献[7]模型最高只达到82%，而本文模型的最高诊断准确率为92%，且在信噪比不同的情况下，本文模型的诊断准确率始终高于另外2种算法。因此，本文模型的诊断准确率较高，并且拥有较好的抗噪声能力。

图4 不同模型故障诊断结果Fig.4 Fault diagnosis results of different models

设定最高诊断煤矿汽车机械设备故障次数为50次，分析3种模型在不同诊断次数下的均方根误差，分析结果如图5所示。根据图5可知，随着诊断次数的上升，不同模型的均方根误差均有所下降，文献[7]模型与文献[8]模型在诊断次数为50次时均方根误差分别为0.032与0.037，而本文模型在诊断次数为20次时，诊断均方根误差下降至0.02，说明此时本文模型可以完成煤矿机械设备全部故障诊断，故障诊断效率高，优势显著。

图5 不同模型的均方根误差Fig.5 Root mean square error of different models

3 结论

本文有效结合低秩鉴别投影算法和改进ART神经网络学习算法，构建基于机器学习算法的煤矿汽车机械设备故障诊断模型，根据低秩鉴别投影算法，提取故障特征，之后采用改进ART神经网络学习算法，通过两阶段的学习，实现煤矿汽车机械设备故障诊断。在未来阶段，可在此基础上加深研究，细化设备故障的类型，提升故障诊断的效率。