变压器多维信息融合及状态评估

李震领，马 辉，李永光，周忠新

(1.中国广核新能源控股有限公司，北京 100070；2.北京金风慧能技术有限公司，北京 100176；3.国网新疆电力有限公司，新疆 乌鲁木齐 830002；4.大唐辽宁分公司，辽宁 沈阳 110000)

电力变压器在电网中有着非常重要的作用，一旦发生故障，会对电力系统造成巨大破坏，因此对电力变压器进行状态评估[1]，在发生故障前检修，有利于变压器的状态维护和管理。目前电力变压器的评估方法主要是基于单个或少量状态参数，而变压器的实际运行状态需要参考多种影响因素，同时由于传统检测方法是将大量单一数据送至中央处理器进行计算，占用了大量通信资源，且效率低下[2]。变压器的状态参数受运行环境影响变化速度快，如果能就地对状态进行评估，再将评估后的结果送至云计算中心，可提高效率。随着泛在电力物联网的建设，不同类型的传感器的信息数据可以互联互通，为变压器的状态参数进行信息融合准备了条件，就地评估变压器状态，然后将评估的状态送至云计算中心，提高了处理效率[3]。利用改进的DS证据理论进行多维度信息融合的大数据技术为解决以上问题提供了可能，综合考虑各影响因素，正确评估变压器运行状态[4-8]。本文对电力设备建立了有效的基于多维度信息融合的电力变压器状态评估与故障诊断体系；利用支持概率距离对证据理论算法进行改进，设计了基于支持概率距离的多维度变压器状态评估模型。

1 变压器参数评估方法

1.1 评估指标选取

反映变压器运行状态参数的指标有很多，选取指标体系时应充分考虑指标的全面性、可行性和科学性，综合考虑指标获取的实时型和准确性，最终选取指标为油色谱指标、油中微水含量、局部放电、套管介损、套管等值电容、绕组温度、顶层油温、变压器外壳振动、铁心接地电流[9]。

1.2 评估指标体系构建

1.2.1 评估指标体系

根据变压器状态参数评估导则，把其运行情况分为4个等级，分别为正常状态、谨慎状态、异常状态和严重状态，不同等级对应不同的限定值[10]。

1.2.2 评估指标权重

为了确定状态量对其健康状况的影响程度，需要计算指标权重，权重系数越大说明其对变压器健康状况影响程度越高[11]。本文的解决方案采用了层次分析法(AHP)和权重系数法协同确定各个确定指标权重。在计算权值之前先要构建判断矩阵，且每一个准则对应一个比较判断矩阵。设判断矩阵A特征值为λ，求出特征向量λmax，然后得到归一化后的ω*，归一化后的权重向量ω计算公式如下[12]：

(1)

式中，rij为第i项指标相对于第j项指标的重要性之比。主客观权重组合W=[w1，w2，…，wn]，其中：

Wi=αωi+βvi(i=1，2，…，n)

(2)

式中，α、β分别为主客观权重系数。

1.2.3 定量指标归一化

由于反应变压器状态参数的指标具有不同的量纲。因此，在评估之前需要进行归一化处理[13]。对于监测数据越低越优和越高越优型指标，量化公式分别为：

(3)

(4)

式中，a1与a2分别为指标数据的最大值和最小值；x为指标的实际测量。每个指标的选取参考《电力变压器运行规程》。

2 变压器多维度信息融合方法

2.1 传统D-S证据理论

D-S证据理论对不确定性问题和多传感器数据信息融合方面具有较强优势[14-15]。假定需要对某个问题进行判定，该问题的答案只能是中的某一个元素，将该相互独立事件的集合U称为识别框架[16]，见式(5)—式(6)。

U={U1，U2，…，Ui，…，Un}

(5)

定义识别框架U的所有子集组成的一个集合，称为U的幂集，记为2U，即：

(6)

在识别框架U中，问题的所有答案都在集合m：2n→[0，1]，并且满足以下关系式：

m(∅)=0

(7)

(8)

式中，m为识别框架U的基本指派概率，即m(A)表示支持A发生的概率。

问题的置信度是通过客观证据进行主观判断得到的，在进行数据融合时需要满足以下条件：①确定目标问题的集合；②将不同传感器采集的信息给出基本概率赋值函数。

2.2 传统D-S合成规则

在同一个目标框架下，通过一定的规则将不同传感器采集到的数据进行融合，利用概率分配函数进行刻画。假设中有2个证据体E1和E2，它们与之对应的基本信任函数函数为m1(X)和m2(X)，相应的交集分别为A和B，即有：

(9)

相应的D-S证据合成规则可表示为：

(10)

式中，m1(X)和m2(X)分别为对应的基本概率赋值函数。

3 改进的D-S理论

传统的D-S证据理论开展证据整合时，可能出现同主观常识相违背的情况。使得传统的D-S证据理论的应用范围受到一定局限。为了避免上述缺陷，本文基于信任因子大小进行权重赋值，并利用支持概率函数对D-S证据理论融合方法进行改进，从而获得期望证据。其主要思路是根据证据和证据集对应的欧式距离，测算出该证据的冲突度。然后利用支持概率距离原理量化可信度。这样可有效降低高冲突类型的证据对合成结果的影响。

3.1 证据冲突度的衡量方法

设定集合框架U=[θ1，θ2，…，θn]，旗下有E1、E2两证据，基本概率设定为m1、m2，焦元设定为A、B，则E1、E2两证据间的Jousselme距离为：

(11)

式中，D为2n× 2n的正定矩阵，其元素分配如下：

(12)

式中，D(A，B)为Jaccard系数，代表焦元A和B之间具备的同质性。

由此，E1与E2证据间的Jousselme距离可变换为：

d(m1，m2)=

(13)

=‖m1‖2

(14)

=‖m2‖2

(15)

(16)

假定有所需论证的事件有n个证据，则结合式(12)、式(13)可设置证据距离矩阵为Dn×n：

Dn×n=

(17)

由此可设置证据Ei到证据集E之间的欧式距离如下：

(18)

式中，Si为证据Ei对应的冲突指标，反映该证据和其余证据间的差异性。

由式(18)可知，证据冲突值越低，同其他证据的同质性越好，则可信度值(Crdi)高，此时满足：si→1，Crdi→0，且可信度随Si增大而减小。为尽可能避免证据在论证过程中的随机因素干扰及降低拟合函数的误差。结合支持概率理论进行欧式距离改进。

3.2 基于支持概率距离的改进

当出现相互冲突的证据体，它们含有不确定性的非单点子集和不确定的子集，D-S合成规则将会产生悖论，出现不能使用的情况。支持概率距离的证据理论优化组合方法流程图如图1所示，整个改进的具体步骤如图1所示。

图1 基于支持概率距离的证据组合方法流程Fig.1 Process of evidence combination method based on support probability distance

(1)计算支持概率。焦元A的支持概率数SPFEm为：

(19)

对于同一个识别框架下的2个证据体，对应的支持概率函数为SPFEm1和SPFEm2，则它们之间的支持概率可表示为：

(20)

对于n个在同一识别框架下的证据体，它们之间的支持概率可表示为：

(21)

(2)求取相似函数。在同一识别框架下的n个证据体，任意两个证据体之间的相似函数为：

(22)

(3)计算证据体之间支持测度函数：

(23)

(4)证据体可信度函数。得到证据体的支持测度函数后，与之相应的证据体的可信度函数为：

(24)

式中，Crd(mi)为证据体Ei被其中最大支持测度的证据体所支持的可信程度。

(5)初始证据源的修正。将每个证据体的可信测度作为折扣率，即αi=Crd(mi)，对这些证据源进行二次修正。

(25)

(6)对修正后的证据源进行融合。采用经典证据理论合成规则对修改后的证据源进行融合：

(26)

4 变压器状态评估

变压器状态评估主要包括信息采集及处理、特征提取、数据融合、模式识别和评估决策。多种传感器采集得到变压器各种特征信息，然后对得到的数据进行分析，使用该模型进行数据融合得到最终决策。本文设计的改进证据理论状态评估模型如图2所示。

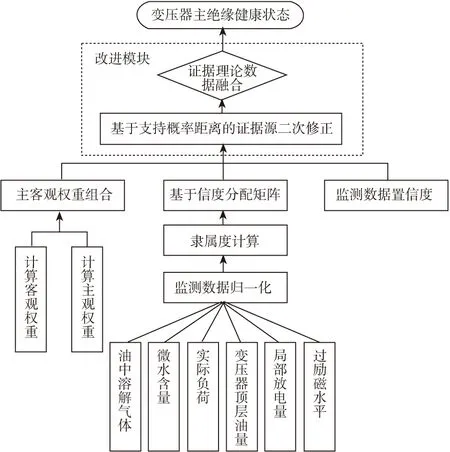
图2 基于多信息融合的电力变压器在线评估模型Fig.2 On-line evaluation model of power transformer based on multi-information fusion

4.1 变压器状态参数评估系统

把电力变压器的状态评估看作成一个多属性评估，将整个评估系统分为3个层级，指标级为各传感器采集的具体信息，上传到子系统级，子系统级进行分为5类，代表了变压器各部分状态，系统级为最终评估结果，具体结构如图3所示。

图3 变压器状态评估系统架构Fig.3 Compressor condition assessment system architecture

将图2中的的变压器状态评估模型使用图3的状态评估系统进行评价，得到相应模型的最终评估结果，而评估指标的权重确定见3.2所述。

4.2 评估指标权重确定

结合常用判断矩阵准则，对判断矩阵中的元素两两比较，然后得出重要性程度表。权重的组合为：

wi=αwi+βvi，i=1，2，…，n

(27)

式中，α和β为判断矩阵得到的主客观权重系数。

4.3 评估指标隶属度估算

采用半梯形隶属度函数来描述评估指标，半梯形的隶属度函数定义：

(28)

这里的k=2，4，6，8，……。

半梯形隶属度函数的分布函数如图4所示：

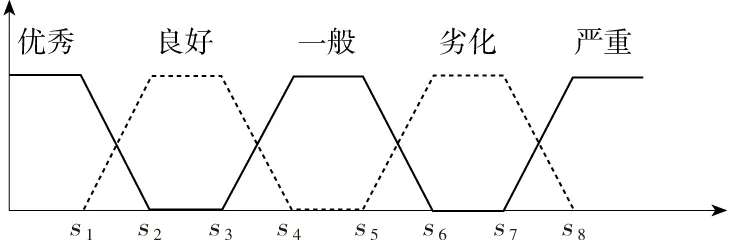
图4 隶属度函数分布Fig.4 Membership function distribution

采用上述半梯模型，划分状态等级概率，可得到判断矩阵P(H)：

(29)

4.4 基于支持概率的证据源修正

根据判断矩阵P(H)以及各状态指标综合权重w进行融合得到综合评估模型M：

M=

式中，wi为第i个评估指标的综合权重；mi(hj)为第i个评估指标在第j个状态等级的基本概率赋值；mi(U)为第i个状态指标的不确定度得到M后，计算n个状态指标之间的支持概率距离

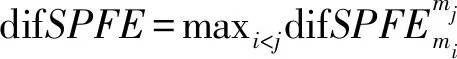
(31)

5 实例分析

以某500 kV变压器的变压器绝缘在线监测数据为例验证所提出方法的状态参数信息融合方法的实用性。按照章节3的步骤，先对传感器采集的状态参数归一化处理，然后计算隶属度函数，最后得到概率分配矩阵，根据概率分配矩阵的结果来判断变压器的状态。

建立变压器状态参数指标的判断矩阵K，计算得到K的相似性程度Cr=0.008 9<0.1，满足相似性要求。计算得到最大特征值4.215，进行标准化计算，得到变压器状态参数指标的主观权重向量为W1=[0.303 0 0.213 7 0.155 4 0.102 8 0.097 6 0.075 8]。利用层次分析法结合熵权法计算客观权重：W2=[0.256 7 0.278 6 0.145 6 0.132 8 0.138 8 0.187 2]。最后得到综合权重值为Wc=[0.260 0 0.228 9 0.163 5 0.143 2 0.1165 6 0.108 7]。对权重进行正规化处理得到W=[1.003 3 0.875 6 0.643 4 0.472 3 0.487 8

0.447 1 0.415 6]。计算置信度CF(Xi)，在此次实验中，500 kV变压器状态指标的置信度[18]选取0.9。得到基本概率分配，其计算公式：

(32)

计算得出基本概率分配矩阵M：

(33)

对初始证据源进行修正融合，同时采用传统D-S证据理论方法和概率证据距离方法对初始证据源M进行融合，与传统证据理论和Jousselme距离融合方法进行，结果比较见表2。

表2 3种变压器状态参数融合方法结果比较Tab.2 Comparison of results of three fusion methods for transformer state parameters

由表2可知，本文方案对决策模型可判定该变压器主绝缘状态评价结果为优，与实际情况相同。传统证据理论方法的评价结果为良，与实际不同；基于Jousselme证据距离的融合方法有较大的模糊性，达不到参数融合评估要求。为说明该法在证据论证结果的准确性，用200组油气样本数据，分别用传统D-S证据理论、基于Jousselme距离的融合及本文方法进行论证。选取变压器常见故障类型进行展示，结果见表3。

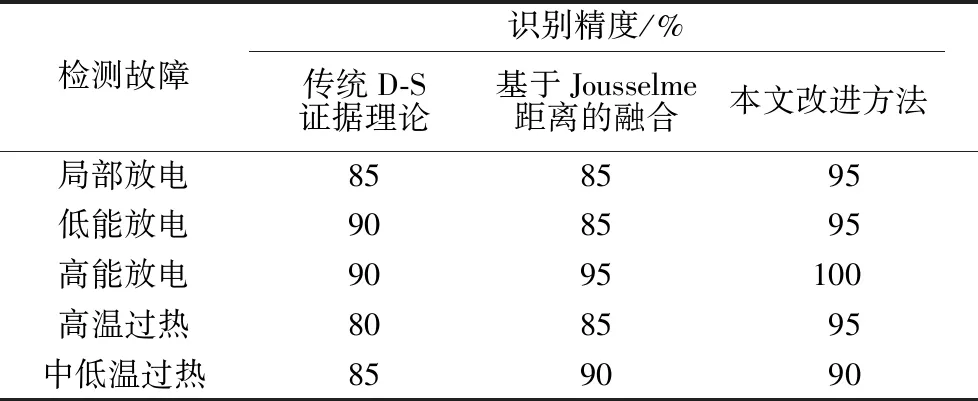
表3 诊断结果展示Tab.3 Diagnosis result display

由表3可知，利用本文方法检测变压器故障类型，可具备更高的识别精度，能很好地克服论证过程中的模糊量干扰。相比于解析关系，利用概率方法更能挖掘变压器故障数据的内部关联。

6 结论

(1)提出了变压器状态参数的评估模型，解决了不同维度参数的权重计算问题。

(2)针对现有变电站设备在线监测系统信息处理中存在“数据过剩而信息不足”的问题，提出基于支持概率距离函数改进D-S证据理论的变压器状态参数多维度信息融合模型，并以变压器为对象进行了验证、分析。所提方法提供了在线监测信息分析和变电站设备状态诊断的信息聚合处理框架，具有很好的应用前景。