火灾下考虑震损的方垫板加强T型节点抗火性能

许继祥, 杨龙龙, 韩建平, 仝义鸽

(兰州理工大学 土木工程学院, 甘肃 兰州 730050)

钢管结构以其优越的力学性能和快速的施工速度被广泛应用于空间结构和大跨结构，如海洋平台、体育馆和火车站等.而T型节点因其节点构造形式简单，传力路径明确，承载能力较高，故常被采用.目前，传统设计中对T型节点仅单独考虑火灾作用或地震作用，未对震后火灾的耦合作用进行联合考虑设计.然而历次事故统计表明，地震后引发次生火灾的概率是极高的，这样在震后火灾作用下T型节点的安全性能储备会不足.另外，由于T型节点的破坏往往发生在主管与支管相交的区域内，故选择在节点的薄弱部位进行加固是非常有必要的.因此，对震后火灾作用下方垫板加强T型圆钢管节点的抗火性能进行分析研究具有重要的现实意义.

目前，国内外许多学者对钢管结构的相贯节点做了大量的研究[1].Lee等[2]通过几何参数分析，对海洋建筑结构中的T型节点的静力强度进行了深入细致研究.王悦等[3]研究了T型圆管相贯节点的静力性能及应力集中情况，讨论了一些基本几何参数对节点应力集中系数的影响规律.翟晓鹏等[4]运用有限元方法分析了T型节点焊接的残余应力与变形，阐述了该T型节点焊接变形的类型、残余应力分布规律及控制焊接变形的措施.Zhu等[5]用试验的方法研究了内置加强环的空心圆钢管T型节点在轴向压力作用下的承载力，并与未加强的T型节点进行了比较分析，发现内置加强环能大幅度提高节点的极限承载力.刘明路等[6-7]对T型圆钢管节点和内置加强环的管节点用有限元方法分别计算了在高温下的极限承载力，通过参数分析发现采用内置加强环的管节点在高温下的承载力会有较大的提高.杨杰等[8-9]用有限元的方法分别对T型方管节点和圆管节点的抗火性能进行了分析，得到了荷载水平与临界温度的关系以及管节点的失效机理.郭永俊[10]对钢桁架T型方管节点和钢桁架加强型T型方管节点的抗震性能进行了分析研究，得到了支管宽度和荷载循环次数对抗震性能的影响.贺欢欢等[11]研究了加强型T型钢连接空间中柱节点的抗震性能，发现T型钢加强连接的延性和耗能能力相比普通T型钢连接提升了30%左右，且具有良好的抗震性能.张红燕等[12-13]对T型圆钢管节点和主管管壁加厚的T型圆钢管节点进行了火灾后的滞回性能和抗火性能研究，分析发现火灾后T型圆钢管节点的滞回性能降低程度不大，管壁加厚能有效提高T型圆钢管节点的耐火性能.Gao等[14]用试验和有限元相结合的方法研究了垫板加强T型节点在火灾后的滞回性能，得到了不同的几何参数对节点滞回性能的影响.Jin等[15]研究了T型圆钢管节点在火灾后的力学性能，发现通过增加支管的直径和主管的厚度能够有效地提高节点的残余强度.王彬彬等[16]和韩祎等[17]分别利用有限元软件研究了张弦梁结构和内配型钢钢管混凝土柱的失效模式、临界温度和耐火极限，为本文后续研究方垫板加强T型节点抗火性能奠定了基础.

综上所述，对于T型节点的研究主要集中在常温和高温下的一些基本力学性能，而未考虑震损这一重要因素，因此本文结合已有的研究结果，提出损伤变量模型，利用有限元软件ANSYS对考虑震损的方垫板加强T型圆钢管节点抗火性能进行了深入分析研究.

1 有限元模型

1.1 计算模型的选取

为准确了解无量纲重要参数支管直径与主管直径的比值β、主管直径与其两倍壁厚的比值γ、支管壁厚与主管壁厚的比值τ、支管外表面到方垫板边缘的距离与支管直径的比值η及垫板厚度与主管厚度的比值τd对火灾作用下考虑震损的方垫板加强T型节点的损伤演化规律、反应过程及临界温度影响规律，本文根据应用于实际工程的节点尺寸及加固类型选取了20组样本进行参数分析研究，各样本详细尺寸构造如图1和表1所示，其中L为主管长度，D为主管外径，T为主管厚度，l为支管长度，d为支管外径，t为支管厚度，ld为垫板长度，td为垫板厚度，δd为支管外部到垫板外边缘的距离.表中主支管直径、主支管壁厚、垫板长度及厚度的单位均为毫米(β=d/D,γ=D/2T,τ=t/T,η=δd/d,τd=td/T).

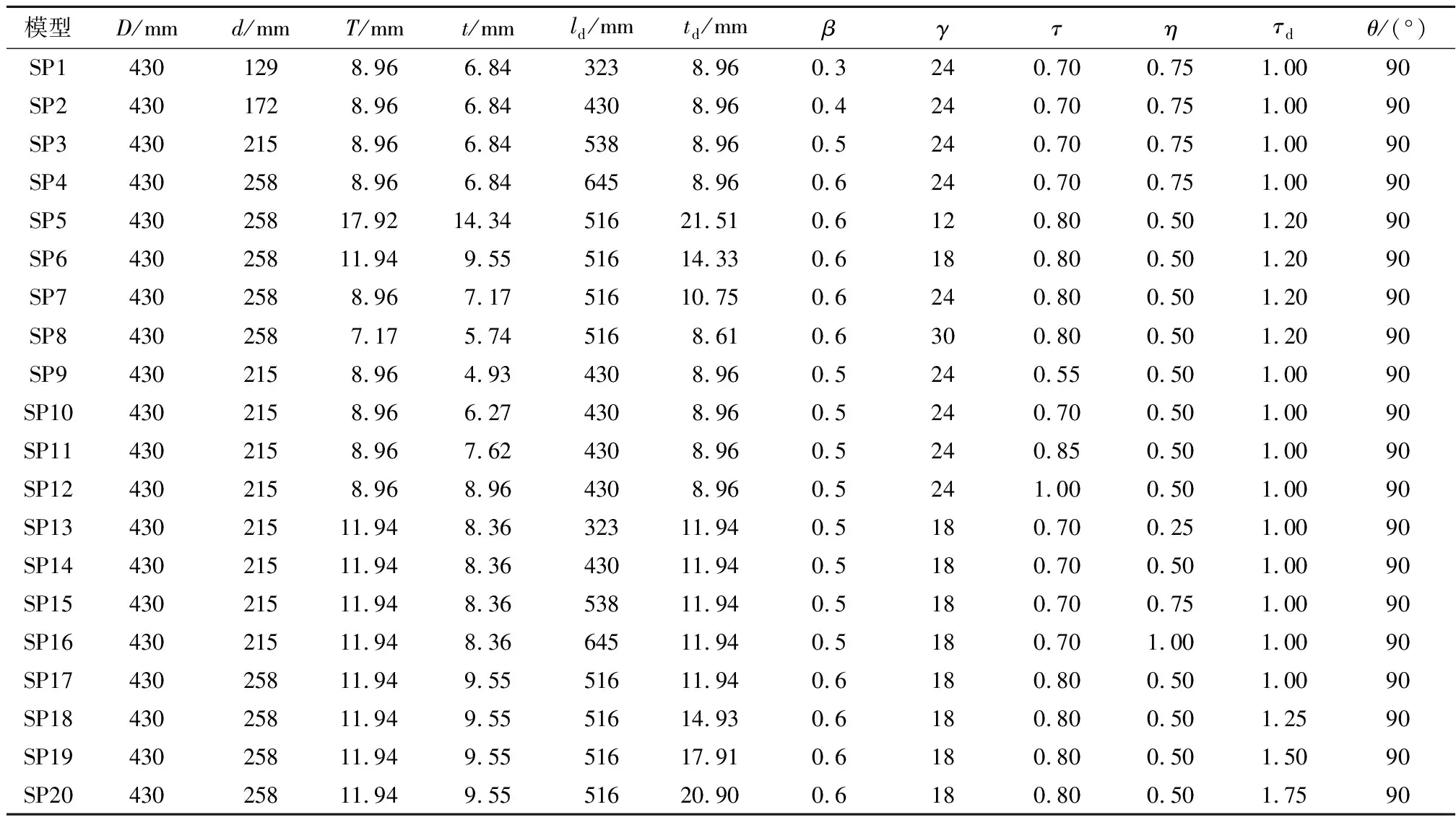
表1 方垫板加强T型圆钢管节点有限元分析模型参数取值Tab.1 Values of finite element analysis models indexes of tubular T-joints with square doubler plate

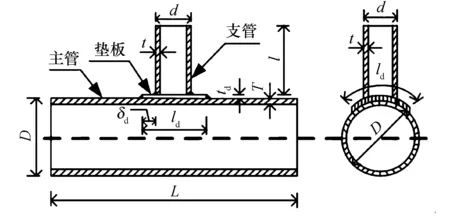
图1 方垫板加强T型圆钢管节点几何尺寸Fig.1 Dimension of tubular T-joint with square doubler plate

1.2 单元类型、网格划分及边界条件

为了准确模拟方垫板和主管表面接触属性，本文选取了ANSYS(14.0)中的实体单元SOLID186单元.SOLID186是一个高阶3维20节点固体结构单元，每个节点有3个沿着x、y、z方向平移自由度，它既考虑了大变形和空间各向异性，也能满足接触功能使用的条件.

为保证计算精度、网格质量和提高计算效率，方垫板加强T型圆钢管节点被切分成了3部分.主支管相交区域为第一部分，主管两端及支管上半部分分别为第二、三部分.由于方垫板加强T型节点的失效主要发生在主支管相交区域，且该区域受力形式及变形较其他两部分复杂，因此在划分网格时，第一部分采取加密措施.第二、三部分的受力及变形相对简单，为提高计算效率，网格划分时采取稀疏措施.最后为保证模型的贯通及整体性，对所有网格进行了压缩与合并.划分网格后的有限元模型如图2所示.

图2 有限元模型Fig.2 Finite element model

本文计算模型的边界条件与已有文献[12]的试验模型的边界条件一致，主管左端全部被约束形成固端，主管右端只允许向右发生水平位移，支管的顶端只允许发生向下的竖向位移.模型的边界条件如图3所示.

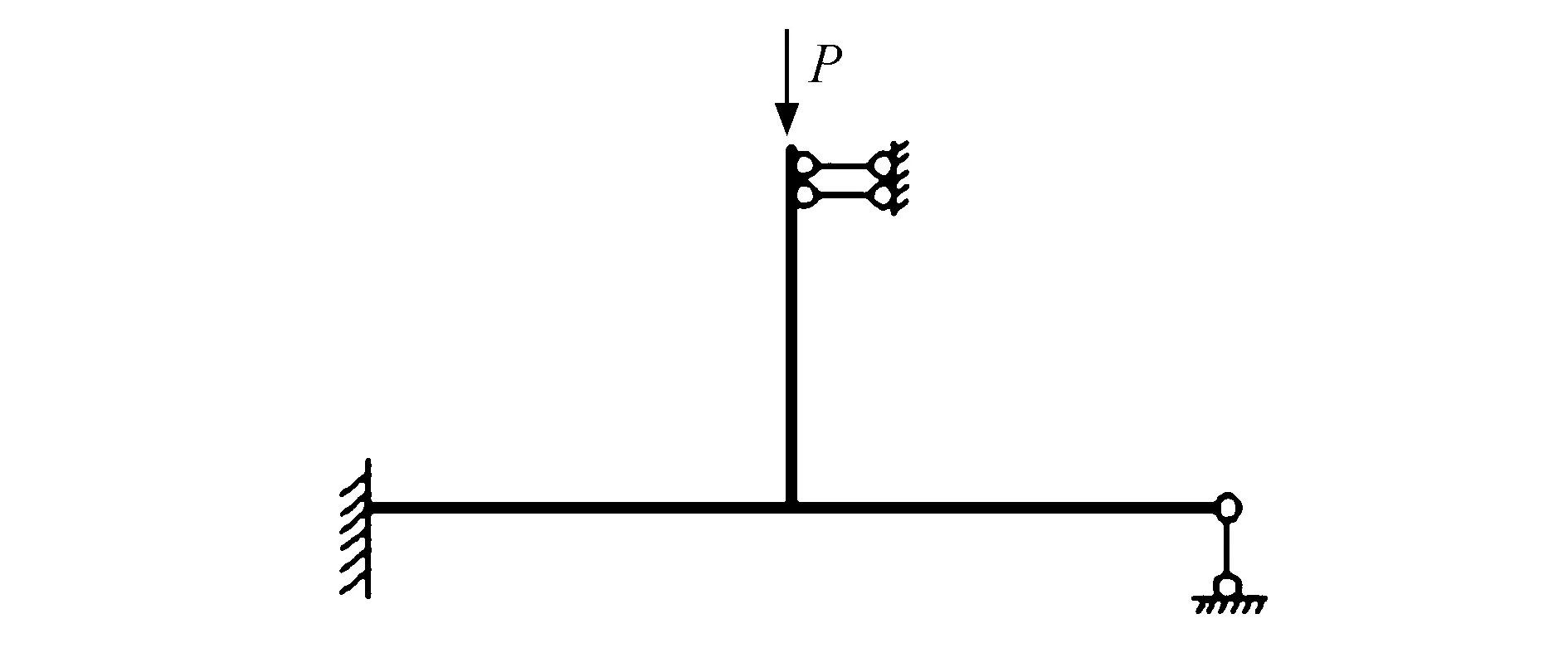
图3 方垫板加强T型节点边界条件Fig.3 Boundary condition of tubular T-joint with square doubler plate

1.3 材料本构模型

常温下，本文采用的钢材弹性模量和屈服强度分别取206 GPa和295 MPa.

高温下钢材的本构关系按我国《建筑钢结构防火技术规范》[18]中的规定取值.

高温下钢材弹性模量:

ET=χTE

(1)

式中：ET为温度Ts时钢材的弹性模量,MPa；E为常温下钢材的弹性模量,MPa；χT为高温下钢材弹性模量折减系数：

(2)

Ts为温度，℃.

高温下钢材屈服强度：

fyT=ηTfy

(3)

fyT为温度Ts时钢材的屈服强度，MPa；fy为常温下钢材的屈服强度，MPa，fy=γRf,f为常温下钢材的强度设计值，MPa；γR为钢构件抗力分项系数；ηT为高温下钢材强度折减系数：

(4)

不同温度下钢材的本构关系如图4所示.

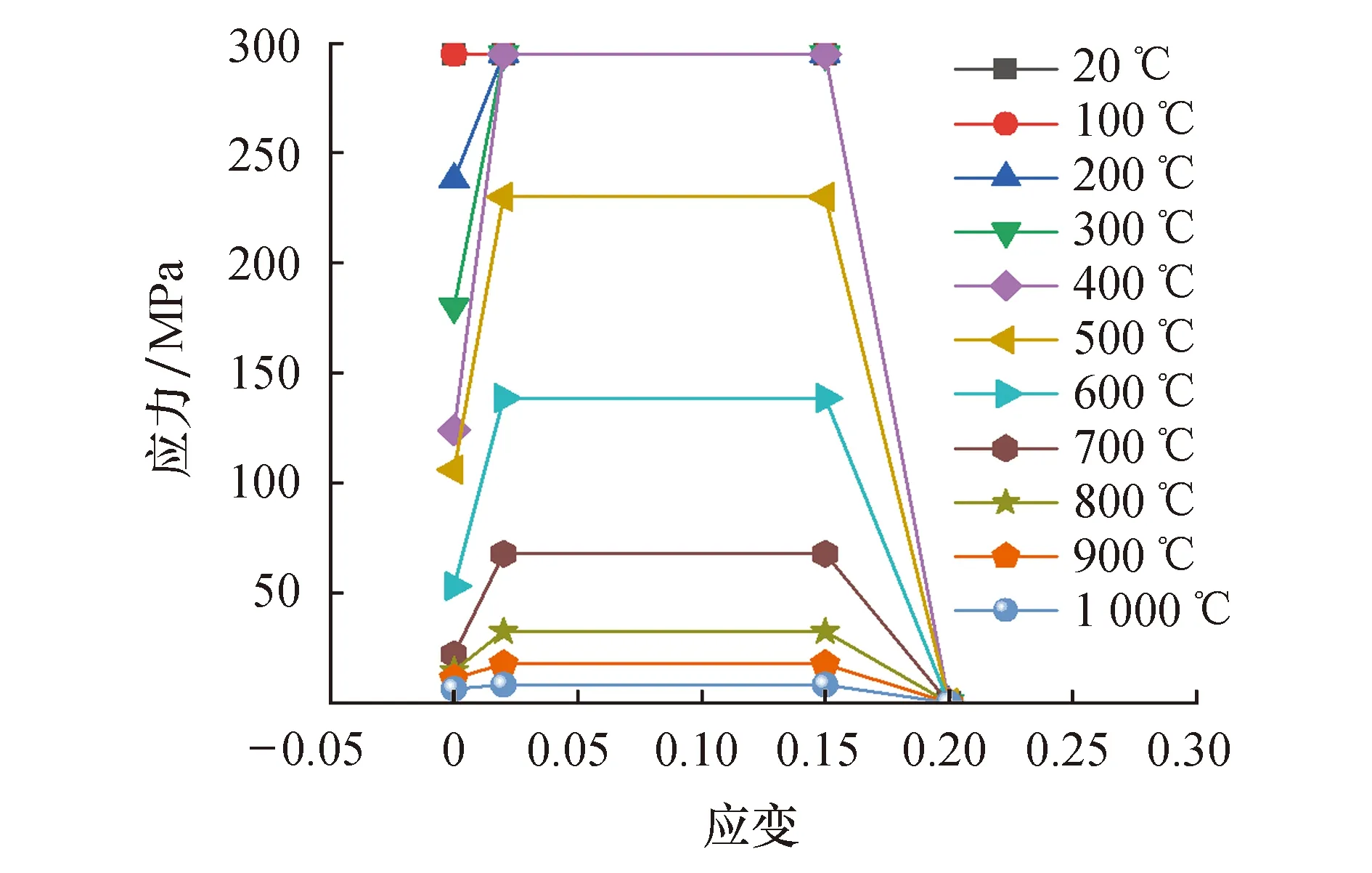
图4 高温下钢材应力-应变关系Fig.4 Stress-strain relationship of steel at elevated temperatures

1.4 升温曲线

为对考虑震损的方垫板加强T型圆钢管节点抗火性能进行研究，本文选取了国内外学者广泛采用的ISO834标准升温曲线，其表达式如下：

T=T0+345lg(8t+1)

(5)

式中：T为升温过程中环境温度；T0为升温前环境温度,20 ℃；t为升温时间.

1.5 算例验证

为了确保有限元分析结果的有效性和准确性，需对有限元模型进行验证.分别选取文献[19]中EX-11试验和文献[20]中SP2试验来进行有限元模型在常温(20℃)和高温后的验证.图5为EX-11试验与有限元的荷载-位移曲线对比，试验得到的极限承载力为305 kN，有限元计算结果为320 kN，有限元结果比试验结果大4.9%.图6为EX-11试验与有限元在方垫板加强T型节点的主管与支管相交处竖向变形的对比.图7为SP2试验与有限元的荷载—位移曲线对比，试验得到的极限承载力为243.21 kN，有限元计算结果为252 kN，有限元结果比试验结果大3.6%.图8为SP2试验与有限元在火灾后的失效模式对比.通过以上比较分析发现：有限元模拟结果与试验结果吻合较好，相对误差均在5%以内，表明用该模型对火灾作用下考虑震损的方垫板加强T型节点进行抗火性能参数分析是可行和有效的.

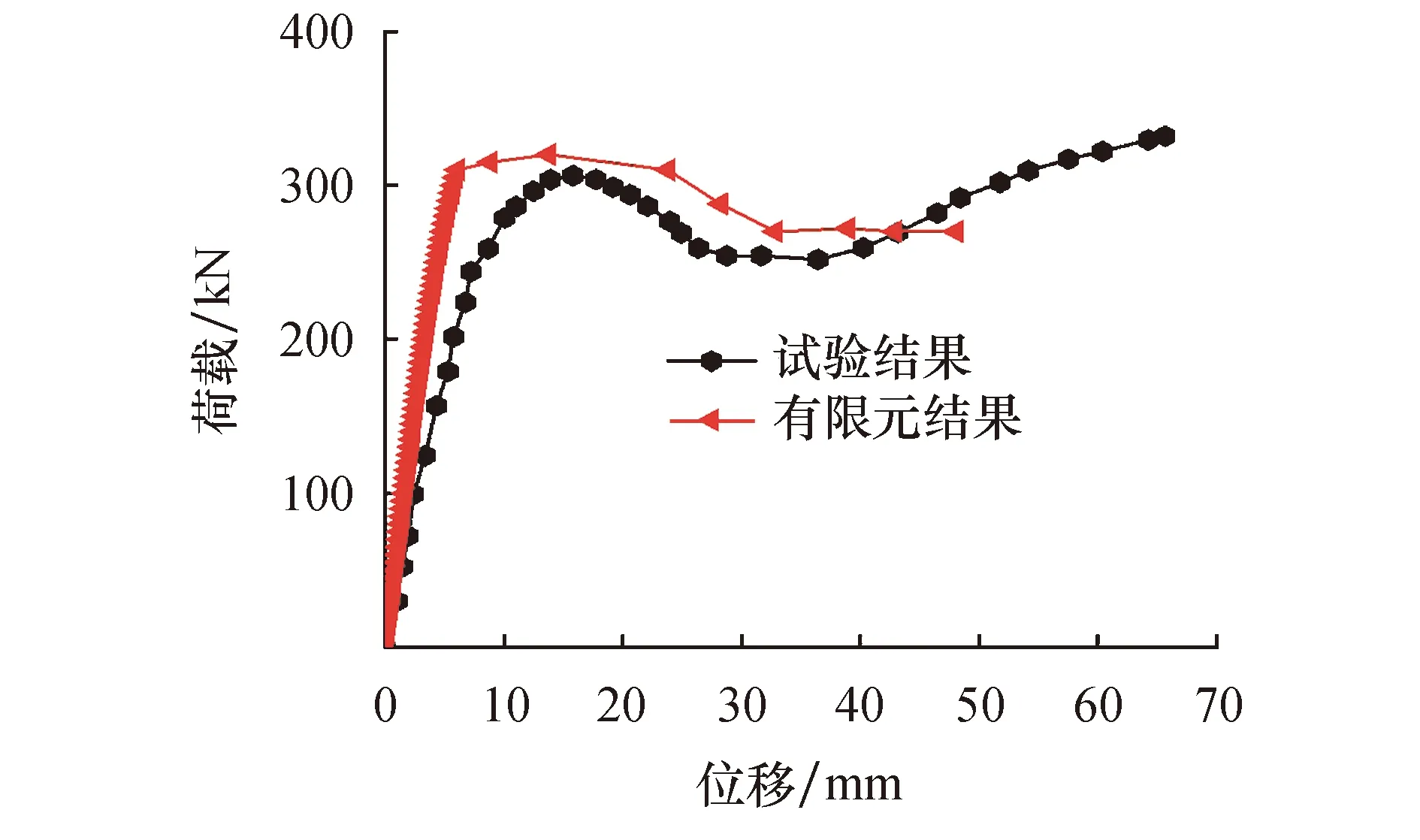
图5 常温下EX-11试验与有限元荷载-位移曲线对比

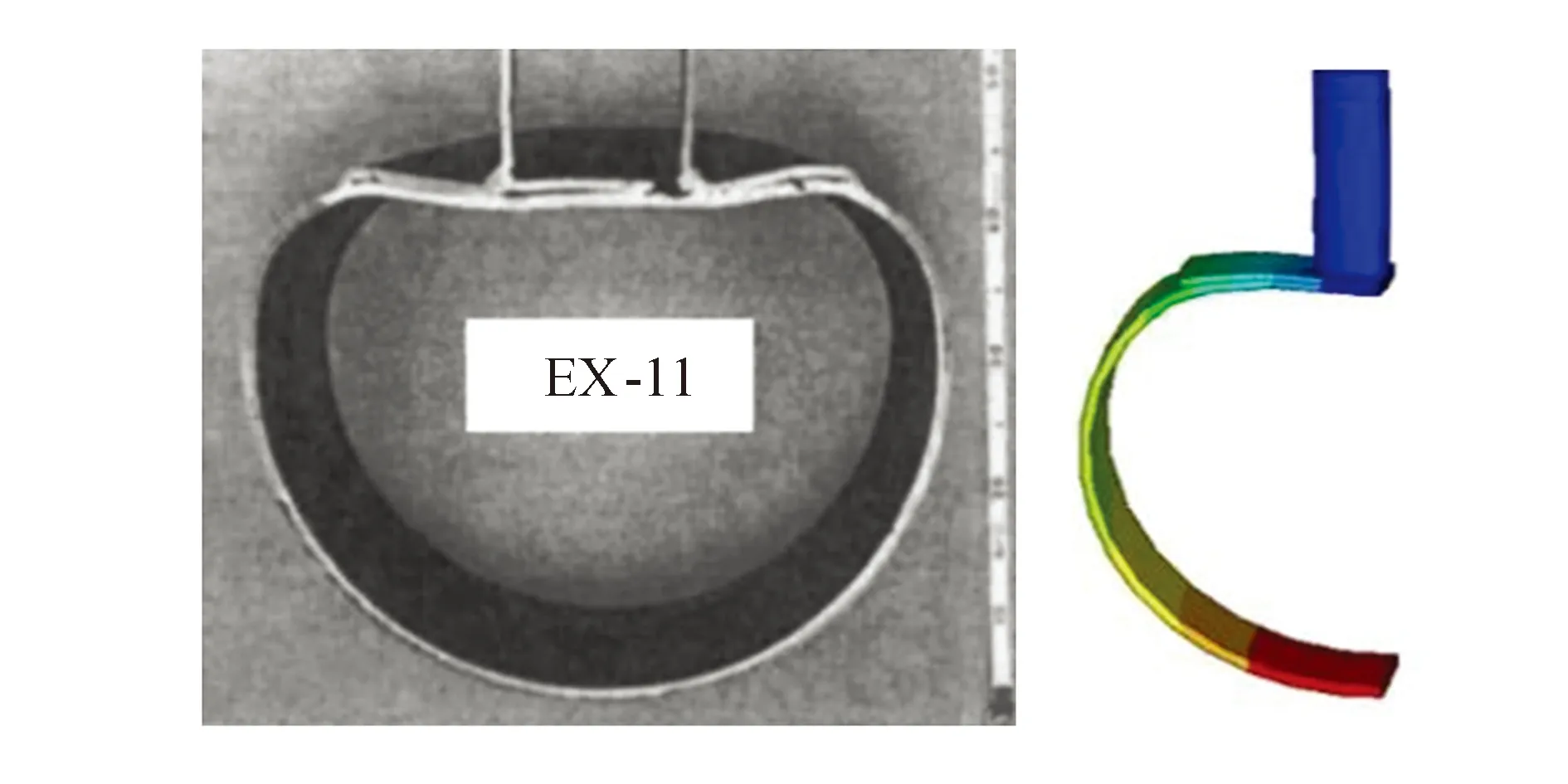
图6 常温下EX-11试验与有限元竖向变形对比Fig.6 Comparison of vertical deformation between EX-11 experiment and finite element model at room temperature

图7 火灾后SP2试验与有限元荷载-位移曲线对比Fig.7 Comparison of load-displacement curves between SP2 experiment and finite element model after fire

图8 火灾后SP2试验与有限元模型失效模式的对比

2 损伤变量模型

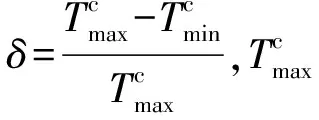
为了考虑震损这一关键因素，本文定义了损伤变量模型，用来描述材料、构件或结构在地震作用下的劣化程度.损伤变量定义如下式：

(6)

3 参数分析

为了准确确定方垫板加强T型节点临界温度，在第三步分析过程中，采用力控制的L2收敛准则来判断程序的收敛性.在确定临界温度时，为了使计算结果与实际受力情况接近，取程序收敛的前一荷载步所对应的温度为临界温度.

3.1 β的影响

由图9可知，当β恒定时，方垫板加强T型节点的临界温度随着损伤变量的增大而减小，且损伤变量对方垫板加强T型节点的临界温度影响较大.

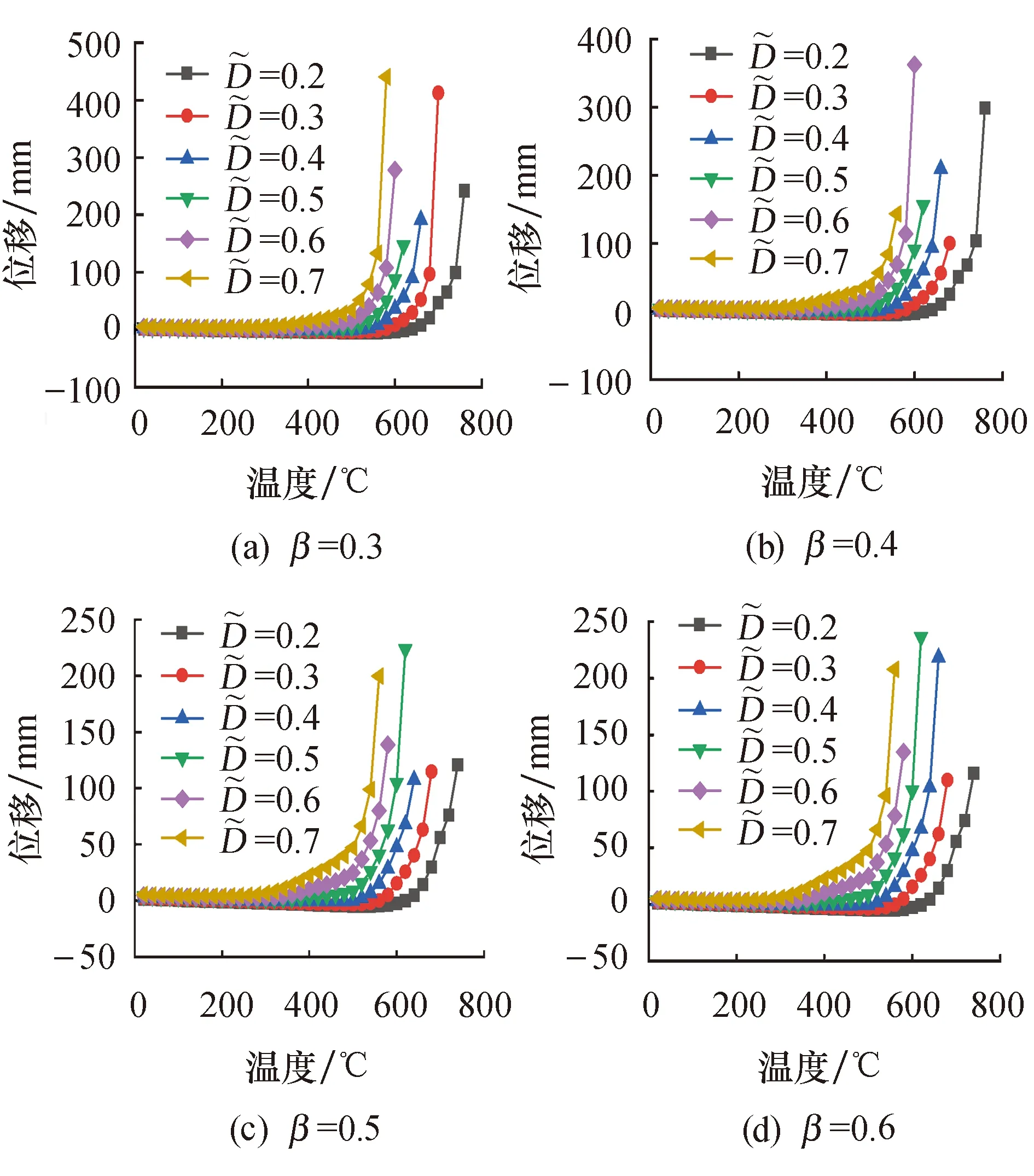
图9 不同参数β的位移-温度曲线Fig.9 Displacement-temperature curves under different β

由表2可知，当β恒定时，损伤变量增大会导致方垫板加强T型节点最大和最小临界温度减小约27%；当损伤变量恒定，直径比β的增大会导致方垫板加强T型节点最大和最小临界温度减小在2%～7%之间.

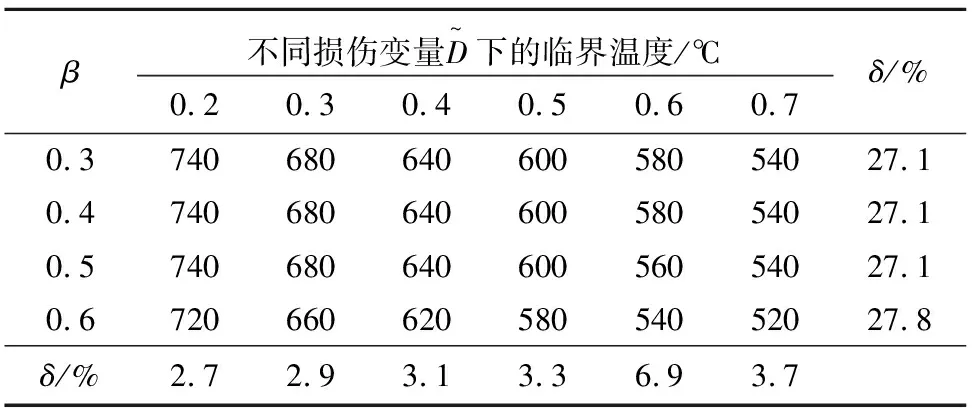
表2 损伤变量和β对临界温度的影响Tab.2 Influence of damage variables and β on the critical temperature

3.2 γ的影响

为了得到参数γ在不同的损伤变量下对方垫板加强T型节点临界温度的影响规律，分别计算了γ=12、18、24、30时方垫板加强T型节点的临界温度.图10为不同参数γ所对应的位移-温度曲线，表3为损伤变量和γ与临界温度之间的关系.

图10 不同参数γ的位移-温度曲线Fig.10 Displacement-temperature curves under different γ

由图10可知，方垫板加强T型节点竖向位移为100 mm左右时所对应的温度为临界温度.对恒定参数γ，随着损伤变量的增大方垫板加强T型节点的临界温度减小，且损伤变量对方垫板加强T型节点的临界温度影响较大.

由表3可知，当γ保持不变而损伤变量增大时，方垫板加强T型节点的最大和最小临界温度会减小约27%，此规律与β大致相同；当损伤变量恒定时，参数γ的增大导致方垫板加强T型节点最大和最小临界温度增大2.7%～7%.

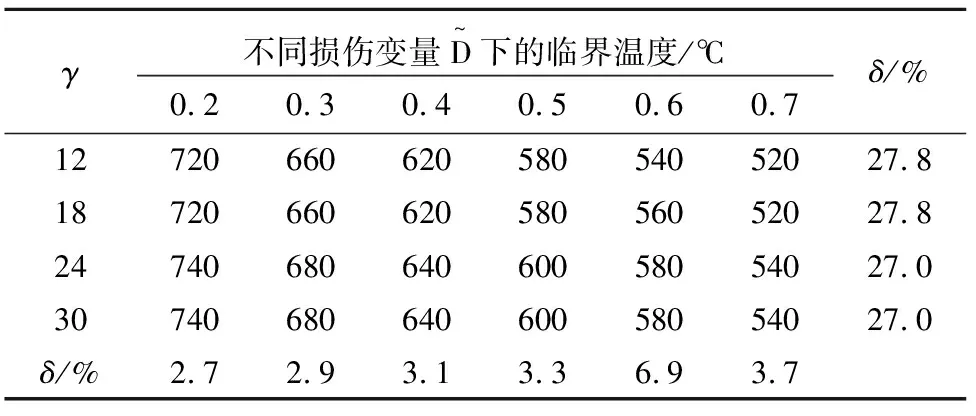
表3 损伤变量和γ对临界温度的影响Tab.3 Influence of damage variables and γ on the critical temperature

3.3 τ的影响

为了得到参数τ在不同的损伤变量下对方垫板加强T型节点临界温度的影响规律，分别计算了τ=0.55、0.70、0.85、1.00时方垫板加强T型节点的临界温度.图11为不同参数τ的位移-温度曲线，表4为损伤变量和τ与临界温度之间的关系.

由图11可知，当参数τ恒定时，方垫板加强T型节点的临界温度随着损伤变量的增大而减小，且损伤变量对方垫板加强T型节点的临界温度影响较大.

图11 不同参数τ的位移-温度曲线Fig.11 Displacement-temperature curves under different τ

由表4知，当参数τ恒定时，随着损伤变量的增大方垫板加强T型节点的最大和最小临界温度会减小约27%，此规律与β和γ大致相同；当损伤变量保持不变时，随着参数τ的增大方垫板加强T型节点最大和最小临界温度会增大2.7%～7%.

表4 不同的损伤变量和τ对对临界温度的影响Tab.4 Influence of different damage variables and τ on the critical temperature

3.4 η的影响

为了得到参数η在不同的损伤变量下对方垫板加强T型节点临界温度的影响规律，分别计算了η=0.25、0.50、0.75、1.00时方垫板加强T型节点的临界温度.图12为不同η所对应的位移-温度曲线，表5为损伤变量和τ与临界温度之间的关系.

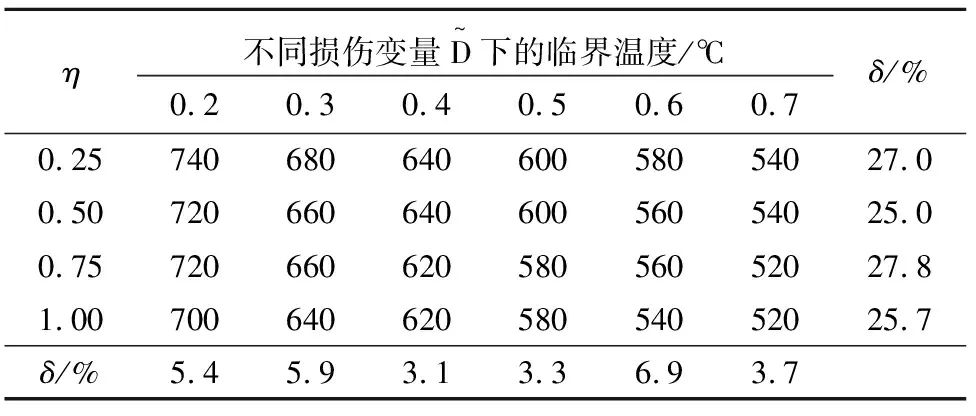
表5 损伤变量和η对对临界温度的影响Tab.5 Influence of damage variables and η on the critical temperature

图12反映了不同的损伤变量和参数η下温度和位移之间的关系.由图12可知，当参数η恒定时，

图12 不同η所对应的位移-温度曲线Fig.12 Displacement-temperature curves under different η

随着损伤变量的增大方垫板加强T型节点的临界温度减小，且损伤变量对方垫板加强T型节点的临界温度有较大的影响.

由表5知，当参数η恒定时，损伤变量的增大会使方垫板加强T型节点的最大和最小临界温度减小，且减小量为25%～27%.与参数β、γ和τ相比，参数η对应的临界温度下降量较大；当损伤变量恒定而参数η增大时，方垫板加强T型节点最大和最小临界温度会减小3.1%～7%.

3.5 τd的影响

为了得到参数τd在不同的损伤变量下对方垫板加强T型节点临界温度的影响规律，分别计算了τd=1.00、1.25、1.50、1.75时方垫板加强T型节点的临界温度.图13为不同τd所对应的位移-温度曲线，表6为损伤变量和τd与临界温度之间的关系.

图13反映了不同的损伤变量和参数τd下，方垫板加强T型节点位移和温度之间的关系.由图可知，对恒定的参数τd，损伤变量的增大会导致方垫板加强T型节点临界温度减小，且损伤变量对方垫板加强T型节点的临界温度影响较大.

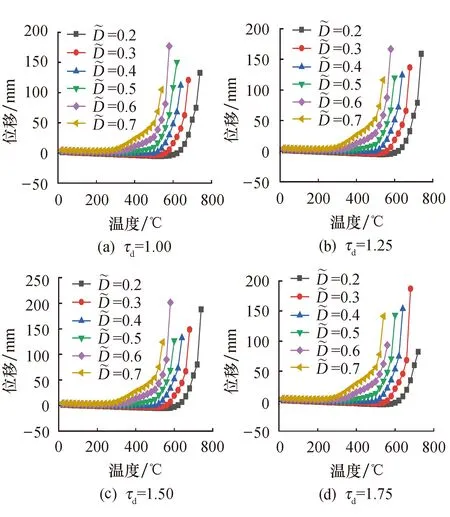
图13 不同τd的位移-温度曲线Fig.13 Displacement-temperature curves under different τd

由表6知，当参数τd恒定时，随着损伤变量的增大，方垫板加强T型节点的最大和最小临界温度减小25%，与参数β、γ、τ和η相比，参数τd所对应的临界温度下降量最小；当损伤变量恒定而参数τd增大时，方垫板加强T型节点最大和最小临界温度几乎不发生变化.

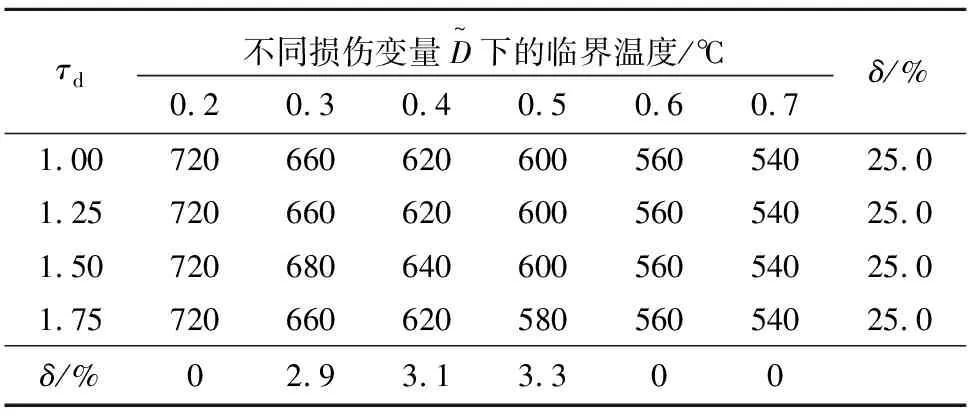
表6 损伤变量和τd对临界温度的影响Tab.6 Influence of damage variables and τd on the critical temperature

4 结论

利用有限元软件ANSYS分析火灾下考虑震损的方垫板加强T型节点抗火性能，由于该类节点形式常用于海洋平台等结构，故以下结论对于分析海洋平台震后火灾性能有一定的借鉴作用.

1) 通过分析损伤变量及参数β、γ、τ、η和τd对方垫板加强T型节点抗火性能的影响，发现损伤变量对方垫板加强T型节点临界温度影响最大，且方垫板加强T型节点临界温度随着损伤变量的增加呈线性减小趋势.当其他参数恒定不变时，临界温度随损伤变量的增大而减小，减小量约为27%.

2) 参数β、γ、τ、η和τd的变化对方垫板加强T型节点临界温度的影响较小，参数β和η的增大会导致方垫板加强T型节点最大和最小临界温度减小2.7%～7%；参数γ和τ的增大导致方垫板加强T型节点最大和最小临界温度增大2.7%～7%；参数τd对方垫板加强T型节点临界温度几乎没有影响.

3) 通过分析损伤变量及参数β、γ、τ、η和τd可知：在进行海洋平台等结构抗火性能设计时，应该通过增加径厚比和壁厚比(即在主管厚度保持不变的前提下通过增加支管厚度和主管直径)来适当提高方垫板加强T型节点在震损下的抗火性能.