余挠对与余倾斜模

吴德军, 移晨刚

(兰州理工大学 理学院, 甘肃 兰州 730050)

倾斜模与余倾斜模是同调代数与代数表示论的重要研究对象.倾斜理论最早出现在Bernstein等[1]证明Gabriel定理中,提出了反射函子和Coxeter函子,并给出了倾斜模的相关定理.Brenner等[2]给出了倾斜模的定理.倾斜模在对偶函子的作用下即为余倾斜模,倾斜模与余倾斜模是代数表示论中一个重要的分支.

余挠对是由Salce在阿贝尔群范畴[3]和在模的近似理论的深入研究中提出[4].记KC=A∩B是余挠对C=(A,B)的核.设M是R-模.则ProdM表示同构于模M的直积的直和项所构成的模类.对于任意的余挠对C=(A,B),若A是余倾斜类,则对n-余倾斜模C,KC=ProdC[4].汪建等[5]给出了完备遗传余挠对的核是倾斜模的直积的直和项的充分条件.受此结论的启发，本文给出完备遗传余挠对的核是余倾斜模的直积的直和项的充分条件.

1 预备知识

在本文中,R是具有单位元的任意环,R-Mod是左R-模范畴.先给出涉及到的一些符号、定义和性质,参见文献[4,6].

符号.设C是R-Mod的全子范畴,n是非负整数.类C⊥,⊥C,C⊥∞和⊥∞C的定义如下：

对于C={C},用C⊥,⊥C,C⊥∞和⊥∞C依次代替{C}⊥,⊥{C},{C}⊥∞和∞⊥{C}.

余挠对.设A和B是在R-Mod中的类.称E=(A,B)是余挠对[3-4],若满足A=⊥B,且B=A⊥.

设C是模类,则C⊆⊥(C⊥),且C⊆(⊥C)⊥.若E=(A,B)是余挠对,则称KC=A∩B为C的核.

称余挠对(A,B)是完备的[4],若满足下面两个条件中的一个条件:

1) 对任意的R-模M,存在正合序列0→M→B→L→0,其中B∈B,且L∈A.

2) 对任意的R-模M,存在正合序列0→D→C→M→0,其中C∈A,且D∈B.

纯内射模.称左R-模M是纯内射模[6],若对每个R-模的纯正合列0→T→N,有Hom(N,M)→Hom(T,M)→0是正合的.用PI表示纯内射模类.显然,每个内射模是纯内射模.

引理1设R是环,M是纯内射模.则(⊥∞M,(⊥∞M)⊥)是完备遗传余挠对.

在下文中,对于R-模M,记KM=⊥∞M∩(⊥∞M)⊥.由引理1知,C=(⊥∞M,(⊥∞M)⊥)时,KC=KM.关于余挠对更详细的内容,可参考文献[4,6].

Gorenstein内射模.称R-模G为Gorenstein内射模[7],若存在内射模正合序列

使得

1)G≅ker(f0);

2) 对任意的内射模L,HomR(L,E)是正合的.

显然,每个ker(fi)和coker(fi)都是Gorenstein内射模.

设n是非负整数.R-模G的Gorenstein内射维数GidRG≤n当且仅当存在R-模正合序列0→G→G0→…→Gn→0,其中Gi是Gorenstein内射模,0≤i≤n[7].由文献[7]命题2.7知,R-模G∈GIn当且仅当G的第n个上合冲Ω-nG是Gorenstein内射模.由文献[7]定理2.29知,若idRM<∞,则GidRM=idRM,并且任意的内射维数有限的Gorenstein内射模是内射模.

以下,GIn={G|GidRG≤n,G∈R-Mod}.若R-模G∈GIn当且仅当G的第n个上合冲Ω-nG是Gorenstein内射模.

引理2设G是R-模,M是纯内射模,n是非负整数.则下述论断成立：

2) 若G∈In,则(⊥∞G)⊥⊆In.

3) 若M∈GIn,则(⊥∞M)⊥⊆GIn.

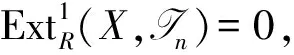
强Gorenstein内射模[9].若存在内射R-模的正合序列

满足:

(1)M≅ker(f)；

(2) 任意的内射R-模L,用Hom(-,L)作用上面正合序列仍保持正合,则称M是强Gorenstein内射模.

由上面定义知,所有的内射R-模是强Gorenstein内射模,强Gorenstein内射模在直积下封闭.文献[9]定理2.7,证明了一个R-模是Gorenstein内射模当且仅当它是强Gorenstein内射模的直和项.通过该证明过程，可以给出下面的引理.

R-Mod的全子范畴C称为厚子范畴,若C在直和项下封闭,并且具有三分之二性质:对R-模正合序列0→A→B→C→0,其中任意两项在C中,则第三项也在C中[10].

内射余挠对[11].设A是有足够多内射模的阿贝尔模范畴.称完备余挠对(W,F)是内射余挠对,若满足W是厚子范畴,且W∩F与内射模对象的类一致.

引理4对于任意的强Gorenstein内射R-模N,下述论断成立：

1)⊥N是R-Mod的厚子范畴；

2) 若N是纯内射模,(⊥N,(⊥N)⊥)是内射余挠对.

2) 由文献[4]推论3.2.12知，(⊥N,(⊥N)⊥)是完备余挠对.另一方面，由1)知⊥N是厚子范畴.又因为内射模是强Gorenstein内射模,所以由文献[11]命题3.6即证.

余倾斜模.左R-模C称为余倾斜模[4],如果满足：

(C1) idRC≤n;

(C3) 存在r≥0和长正合序0→Cr→…→C0→W→0，其中Ci∈ProdC,i≤k,W是R-Mod的内射余生成子.

若n≤ω,并且C∈In的余倾斜模,则C称为n-余倾斜模.类⊥∞C(⊆R-Mod)是由C诱导出的n-余倾斜模类.显然,(⊥∞C,(⊥∞C)⊥)是遗传余挠对,称为由C诱导的n-余挠对.由文献[12]定理4.2的证明，可以得到下面的引理.

引理5设C=(A,B)是环R上的完备遗传余挠对.若A是n-余倾斜模,则对于余倾斜R-模C,有KE=ProdC.

2 主要定理的证明

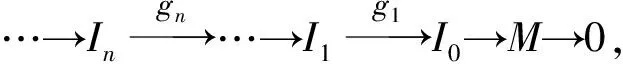
引理6设G是R-模,n是正整数.则下列条件等价：

1) GidRG≤n;

2) 存在R-模正合序列

其中:idREj≤n,使得对任意的内射R-模L,有

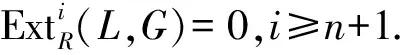
2)⟹1) 要证明GidRG≤n,即证明Ω-nG是Gorenstein内射模.考虑正合序列0→coker(fm+2)→Em→coker(fm+1)→0.由文献[6]引理8.2.2知,可以构造交换图,如图1所示.

其中:行和列都是正合的,Ft,k是内射模.因为对所有的n≥0,idREm≤n,所以Ω-nEm是内射模.记Ω-nG=Ω-ncoker(f1),则有下面正合的交换图,如图2所示.

图1 交换图

Fig.1 Commutative diagram

…→Ω-nEm→Ω-nEm-1→…→Ω-nE0→Ω-nG→0

Ω-ncokerfm+1

0 0

图2 交换图

Fig.2 Commutative diagram

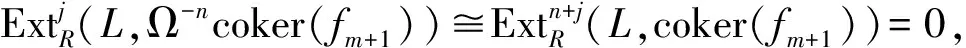
引理7设R是环,C=(A,B)是R-模完备遗传余挠对.如果KE⊆In,B⊆GIn和G∈B,那么存在强Gorenstein内射模N∈B,使得Ω-nG是N的直和项.

证明设G∈B,因为(A,B)是完备余挠对,所以存在R-模正合序列

Ω-ncokerfm+1

0 0

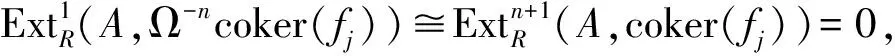
其中:coker(h-j)是Gorenstein内射模,并且coker(h-j)∈B,j≥1.另一方面，Ω-nG是Gorenstein内射模,且Ω-nG∈B,所以存在R-模正合序列

其中:Ej是内射模,coker(hj)是Gorenstein内射模,并且coker(hj)∈B,j≥1.

将E-和E+连接起来,获得内射模正合序列

使coker(hj)是Gorenstein内射模,且coker(hj)∈B.设N=∏coker(hj),则由引理3知,N是强Gorenstein内射模,故N∈B,且Ω-nG是N的直和项.

命题1设M是纯内射模，n是非负整数.则下列条件等价：

1) 存在强Gorenstein内射模N∈(⊥∞M)⊥,使得Ω-nM是N的直和项;

2) (⊥∞M)⊥⊆GIn,KM⊆In.

2)⟹1) 由引理1知,C=(⊥∞M,(⊥∞M)⊥)是完备遗传余挠对,再由条件知,B=(⊥∞M)⊥⊆GIn,KM⊆In,则由引理7可证.

注1假设M是纯内射模且idRM≤n,N是强Gorenstein内射模.Ω-n(M⊕N)可认为是Ω-nM⊕N.因为Ω-nM是内射模,所以显然Ω-nM⊕N∈(⊥∞(M⊕N))⊥是强Gorenstein内射模.因此,M⊕N满足命题1的条件1).

证明因为idRM≤n,所以存在正合序列

其中：Ej是内射模.因为N是强Gorenstein内射模,所以存在正合序列

则有

0→M⊕N→E0⊕E→…→En⊕E→0

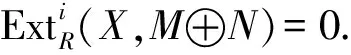
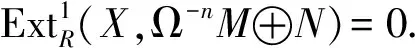
引理8[5](维数转移) 设R是环,n是正整数,M是R-模,存在R-模正合序列0→K→Tn→…→T1→L→0,则下述论断成立：

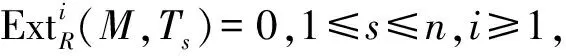
定理1设R是环,C=(A,B)是完备遗传余挠对,In(GIn)是内射维数(Gorenstein内射维数)至多是n的R-模类.则对于任意正整数n,下述条件等价：

1) KC=ProdC,C是n-余倾斜模;

2) KC⊆In,B⊆GIn,KC在直积下封闭;

3) KC⊆In,A=⊥∞C∩⊥∞X,其中C是n-余倾斜模,X是强Gorenstein内射R-模类;

进而,若对于纯内射模G,A=⊥∞G,并且Ω-nG是G的第n次上合冲,则以上条件等价于:

4) A=⊥∞C∩⊥∞N,其中C是n-余倾斜模,N是强Gorenstein内射模,且N是纯内射模;

5) KC在直积下封闭,存在强Gorenstein内射模M∈B,且M是纯内射模,使得Ω-nG是M的直和项;

6) KC在直积下封闭,存在强Gorenstein内射模N∈B,且N是纯内射模,使得⊥(Ω-nG)=⊥∞N.

证明1)⟹2) 由假设知,A∩B=ProdC,C是n-余倾斜模,idRC≤n,所以KC⊆In.因此,只需证明B⊆GIn.设M∈B,下证GidRM≤n.因为(A,B)是完备余挠对,所以存在R-模正合序列

使得Xj∈KC,coker(fi)∈B.存在R-模正合序列0→Cn→…→C0→W→0,其中Ci∈ProdC,W是内射余生成子.从而,对于任意内射模WI,存在R-模正合序列

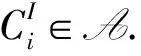
应用引理7，对于任意L∈B,存在强Gorenstein内射模NL∈B,使得Ω-nL是NL的直和项.设X={NL|L∈B},则{C}∪X⊆B.下证A=⊥∞C∩⊥∞X,显然A⊆⊥∞C∩⊥∞X.下证A⊇⊥∞C∩⊥∞X.假设任意的模L∈B和H∈⊥∞C∩⊥∞NL,由文献[12]定理3.11知,CogennC=⊥∞C,所以存在R-模正合序列

0→H→C′0→C′1→…→C′n-1→Kn→0

又因为C′j∈KC,0≤j≤n-1,由引理8中2)知：

L∈(⊥∞C∩⊥∞NL)⊥⊆(⊥∞C∩⊥∞X)⊥

因为L是B任意的模,所以B⊆(⊥∞C∩⊥∞X)⊥.因此，⊥∞C∩⊥∞X ⊆A.故A=⊥∞C∩⊥∞X.

由条件知,KC⊆In,则K∈In.因此

即K⊆(⊥∞C)⊥.显然K∈⊥∞C.由KC=ProdC知,K∈ProdC.因此KC⊆ProdC.即证.

3)⟹4) 由条件知,对于纯内射模G,A=⊥∞G,C=(⊥∞G,(⊥∞G)⊥)是完备遗传余挠对,用2)⟹3)相似的证明方法知,A=⊥∞C∩⊥∞NG,其中NG是强Gorenstein内射模,使得Ω-nG是NG的直和项.

2)⟹5) 由引理7可证.

5)⟹2) 由条件知,(A,B)=(⊥∞G,(⊥∞G)⊥),KC=KG.由命题1可证.

6)⟹5) 由条件知,⊥∞(Ω-nG)=⊥∞N.因为N是强Gorenstein内射模,所以⊥N=⊥∞N.因此,⊥∞(Ω-nG)=⊥N.进而,Ω-nG∈(⊥N)⊥⊆GIn,应用引理4中2)知,(⊥N,(⊥N)⊥)是内射余挠对.由引理7知,存在强Gorenstein内射模M∈(⊥N)⊥,使得Ω0(Ω-nG)是M的直和项,显然Ω0(Ω-nG)=Ω-nG.由条件知,N∈B=(⊥∞G)⊥.因此,M∈(⊥N)⊥=(⊥∞N)⊥⊆(⊥∞G)⊥,故M∈(⊥∞G)⊥.即证.

推论1设C是n-余倾斜模,N是强Gorenstein内射模,且N是纯内射模.则KC⊕N=ProdC.

证明记C=(⊥∞(C⊕N),⊥∞(C⊕N)⊥),A=⊥∞(C⊕N)=⊥∞C∩⊥∞N.由定理1中4)⟹1)即证.