基于聚类和随机矩阵理论的用电行为刻画方法
吴丽珍, 张永年, 陈 伟, 郝晓弘
(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 国家级电气与控制工程实验教学中心, 甘肃 兰州 730050)
随着我国能源互联网战略的不断推进,电网建设也趋向于智能化,用户用电量和用电行为方式也呈现出多元化的特征[1].在我国电力体制改革的背景下,电力行业逐步进入以市场为导向的新层面,同时因为体验型经济逐渐兴起,传统的对电力用户无差化服务已无法满足用户多样化需求,因此,准确地对电力用户用电行为分析,实现对电力用户用电的精准分类并提供差异性服务成为了供配电领域的发展关键[2-3].研究电力用户的基本信息数据对用户用电行为的影响对于用户用电策略的制定有着重要意义.
近年来,国内外学者通过用电大数据挖掘,在用户用电行为分析方面做了相关研究.张斌等[4]针对单一聚类方法的不足,通过对不同聚类方法优缺点的分析,提出一种层次聚类与划分聚类相结合的聚类方法用于负荷聚类.朱文俊等[5]在利用自适应K-means算法对电力用户进行局部聚类分析基础上,提取局部负荷曲线并构建局部模型,并利用传统聚类算法对局部模型进行分析,获取全局负荷曲线模型,进行用户用电态势感知.但是,上述方法由于算法需要处理的数据类型较多,且存在大量的无用数据,因此数据处理所需时间较长.陆俊等[6]提出一种基于用电特征优选策略的自适应用户用电行为分析方法,以减少计算复杂度和提高聚类准确率,但其仅对用户用电特征数据进行处理分析,而对于用户基本信息数据并未加以利用,降低了电力用户分类的准确性.目前大多数研究是利用用户数据对用户进行分类,对于在利用有限的数据信息情况下,分析电力用户的基本信息数据与用户用电行为之间的关联性方面的研究较少,而该方面研究对于电力公司用电策略的制定有着重要意义.随机矩阵理论(random matrix theory,RMT)作为一种统计学工具,在分析数据之间关联性方面有着较为突出的效果.
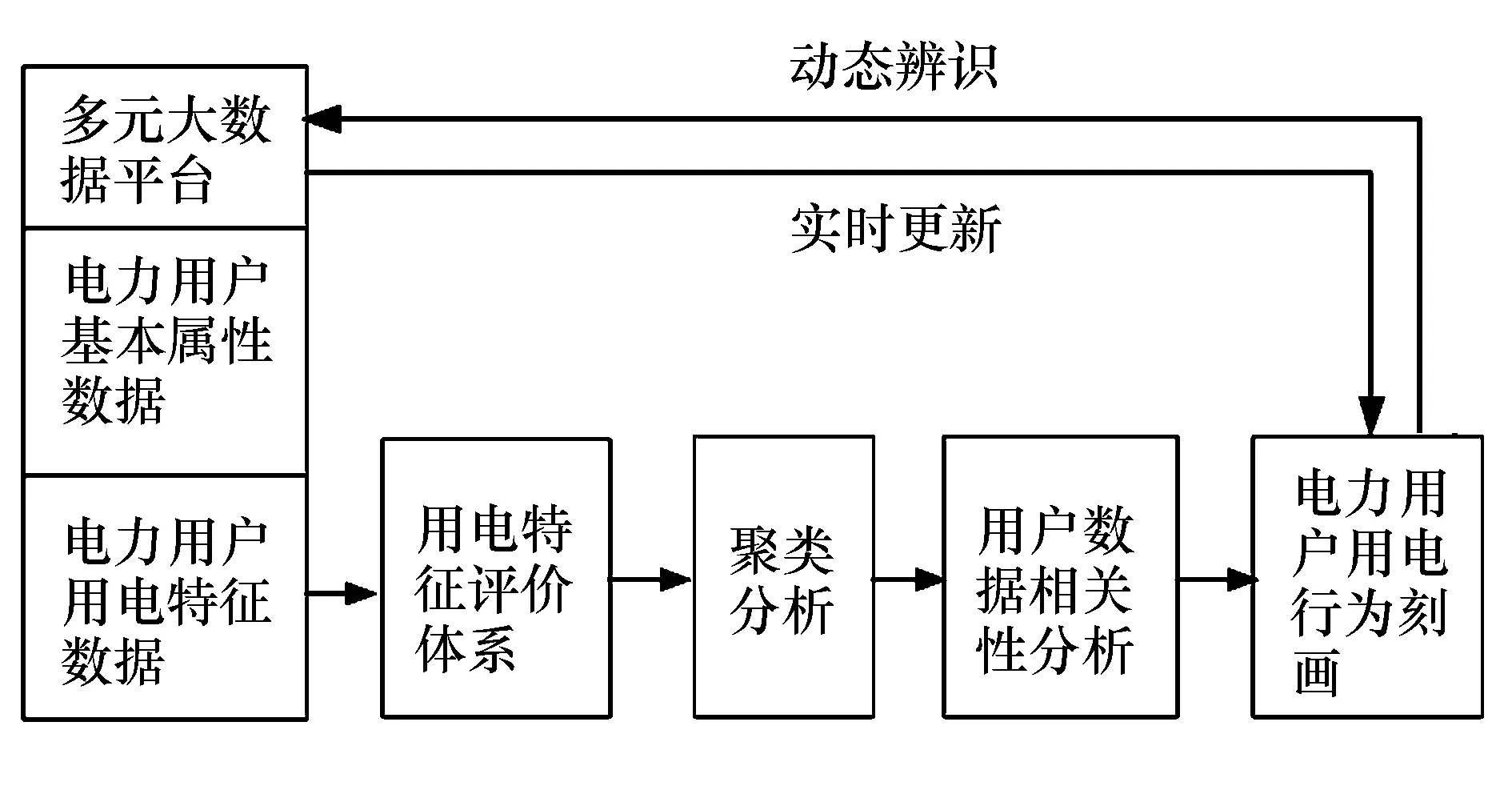
因此,本文提出一种基于K-means聚类和随机矩阵理论的电力用户用电行为刻画方法.首先,通过熵权法构建用电特征评价体系,选取用户优选用电特征数据,利用K-means聚类算法对电力用户进行分类.然后,利用随机矩阵理论对各用电群体构建用电行为分析模型,分析基本信息数据对各类用户用电行为的影响程度,刻画不同用电模式用户的用电行为,为供电公司制定营销策略提供理论支撑.
1 用户群体划分方法
对于一个电力用户个体,所采集的数据主要包括两类,一类是电力用户的基本属性数据,包括经济情况、气候数据、用户理想电价、节假日等数据,通过对该属性分析可以预估电力用户对于电力的消费能力[7].第二类是电力用户的用电特征数据,主要包括历史电价、历史负荷曲线、日负荷率、峰时耗电量等,从其中可以了解用户的用电模式及用电习惯[8].由于供电结构的改革,如何给用户提供精准化用电服务成为了很重要的一个研究部分.但是在实际情况中,供电公司为每一个用户提供一个用电策略显然是不可能的,因此,需要对具有同种用电行为模式的用户进行群体划分,利用群体策略来替代个体策略,可以提高供电公司的服务效率.
1.1 用电特征量的优选方法
由于用户对不同用电特征的行为响应不同,通过选取对该类用户最有效的用电特征评价体系来刻画用户用电行为,能够去除多余信息,减少数据量,提高分析速度.此外,用电特征与用户用电行为之间关系紧密,各用电特征间存在较大的关联性,分析中存在信息冗余以及重叠现象,会使得分析效果变差.因此,可以考虑利用熵权法求取权重值有效评价用户用电特征.
设有m个用户群体,n个用电特征,得到评价体系的初始数据矩阵:X={xij}m×n.其中,xij表示在第j个用电特征在第i个用户下的特征数值.由于不同用电特征的量纲不同,为了使得不同量纲之间具有可比性,需要对原始数据标准化,其变换公式如下式所示[9]:
(1)
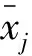
特征信息比重pij和信息熵值hj计算公式[10]为
利用信息熵值hj求解权重值wj,计算公式为
(4)
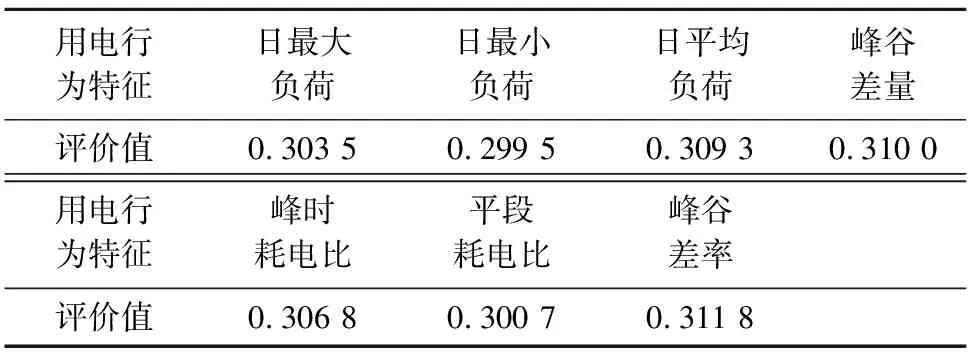
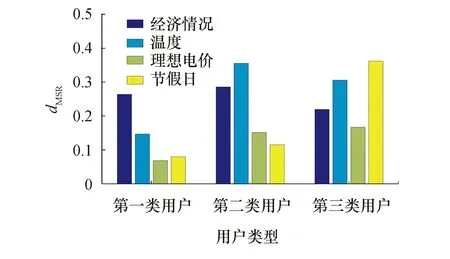
式中:0 根据评价方法对该类用户的各用电特征进行评价,选取最优用电特征,并建立优选特征集.从每次搜索中选取权重值最大的用电特征放入已选特征集中,并利用已选特征集进行特征分析,直到其性能达到目标值为止.优选特征集评价值与目标值为 式中:Y(j)为已选特征优选集评价值;wj为第j个用电特征的权重值;C为目标阈值,一般取值为0.1~0.5;E为目标值.当E值小于C时,优选特征集选择结束. 用电行为特征优选方法流程图如图1所示. 图1 用电行为特征优选方法流程Fig.1 Flow chart of user behavior feature optimization 聚类分析是在不了解一批样本中其类别或者其他特征归属的情况下,利用某种相似性度量方法,将特征极为相似的样品归为一类的方法.目前常用的聚类方法有K-means算法、K-medoi算法、Clarans算法、Pam算法等.由于K-means算法简单,易于实现,算法放入可伸缩性较好,且适用各种数据类型,已经在数理统计、模式识别和数据挖掘等领域适用[11-12].由于是利用优选用电特征数据对电力用户用电行为进行刻画,很大程度上减少了数据量.算法进行聚类分析时,每次的迭代过程所用时间更少,在总体时间复杂度上面会远小于传统聚类算法.因此选用K-means算法进行聚类分析.算法步骤为: 步骤1:根据优选特征集,提取样本用户群体优选用电特征数据集X={x11,…,x1i;x21,…,x2i;xn1,…,xni},其中n为用户个数,i为优选特征个数,xni表示第n个用户的第i个用电特征值. 步骤2:数据处理.由于数据中存在不同特征量,因此数据具有不同的性质属性和度量单位,为使得数据具有同样的标准,需要对数据进行中心化变换,如下式所示: (7) 式中:xmi是第m个数据所包含的第i个特征;m=1,2,…,n. 步骤3:令迭代次数I=1,选择初始聚集点为C1,C2,…,Ck,记为Cj(I),j=1,2,…,k. 步骤4:计算每一个数据点与所选k个聚集点之间的欧式距离d(x′mi,Cj(I)),m=1,2,…,n;j=1,2,…,k.如果满足下式,则x′mi∈Cj: (8) 步骤5:计算k个新的聚类中心: (9) 式中:N为Cj中聚类点个数. 步骤6:判断若Cj(I+1)≠Cj(I),j=1,2,…,k,则I=I+1,返回步骤3;否则算法结束. 步骤7:输出聚类结果,算法结束. 聚类的效果用目标函数U来表示: (10) U值越小,聚类效果越好.因此,算法通过对U值的不断优化来得到更好的聚类结果,当U值为极小值时,聚类结果最优. 利用K-means聚类法对电力用户群体划分后,为了对用户用电行为进行刻画,需要分析用户基本信息数据和用户用电行为之间的关联性.RMT能够对包含多维数据信息的矩阵进行随机性分析,挖掘数据间的信息与关联性,得到用户用电行为与基本用户信息之间的相关性和联系,从而实现对用户用电行为的刻画[13]. 协方差矩阵是数理统计以及其他领域分析系统状态较为常用的一个统计量.M-P律是随机矩阵理论中可用于描述大维协方差矩阵的特征值分布情况,并通过其平均谱分布情况来反映数据间的相关性,且具有较强的实用性. (11) 平均谱半径(mean spectral radius,MSR)是随机矩阵理论中常用的一种线性特征值统计量,利用特征值在复平面上与原点的距离来反映随机矩阵特征值的分布情况,其定义如下式所示[16]: (12) 式中:LMSR为随机矩阵的平均谱半径;λi(i=1,2,…,p)为矩阵的第i个特征根. 为分析用户基本信息对电力用户用电模式的影响,将用户基本信息数据和用户用电特征数据建立增广矩阵,利用增广部分对于原用电特征数据的影响程度来表征两者之间的相关性. (13) (14) (15) (16) 将所得特征数据进行标准化处理后,按如下步骤建立增广矩阵模型.假定所得到的用户数据中,存在m个用户,每个节点选取用电特征mc个,用户基本信息类型有mf个.用户用电特征数据构成基本状态矩阵为Bc∈C(m×mc),用户基本信息数据构成影响因素矩阵为Bf∈C(m×mf).将基本状态数据矩阵与影响因素矩阵构建为状态增广矩阵A: (17) (18) 采用随机矩阵理论中的平均谱半径作为矩阵数据间相关性分析的指标.为排除状态数据与影响因素数据中重复数据所带来的干扰,定义增广矩阵谱半径之差作为指标,其公式[18]为 (19) 利用随机矩阵理论通过数据间的相关性来刻画用户用电行为,为电力公司对用户用电相关服务工作提供理论支持.用户用电行为刻画方法流程图如图2所示. 图2 用户用电行为刻画方法流程Fig.2 Flow chart of user behavior description method 本文用于算例分析的数据为甘肃省武威市电网某区域的实际量测数据.使用MATLAB软件搭建仿真平台,分析所有用户数据,对用户用电行为刻画方法进行验证. 利用用电行为特征优选方法,计算各用电特征的评价值,求取最优特征集.令目标阈值C=0.2,仿真计算结果见表1. 表1 用电特征评价Tab.1 Evaluation of power consumption feature 利用表1中用电特征评价值求取目标值E,所得结果为E=[1, 0.498 6, 0.332 2, 0.247 8,0.196 9,0.163 2,0.139 8],当E≤C时,共迭代了4次,此时最优特征集中包含有评价值较高的5个优选特征,即为峰谷差率、峰谷差量、日平均负荷、峰时耗电比以及日最大负荷.因此,选取这5个用电特征作为L1的优选特征,并将对应的用电特征数据作为对群体L1进行聚类分析所需的数据. 采用K-means聚类算法,分别对使用优选特征集和未使用优选特征集两种情况进行聚类分析.计算结果为:当使用优选特征集时,聚类迭代次数为9次,准确率为95.6%,聚类所需时间为0.309 s.未使用优选特征集时,聚类迭代次数为26次,准确率为97.2%,聚类所需时间为0.605 s.结果表明,选择优选特征集进行聚类分析相比于未选用优选特征集聚类分析的准确率略微下降,但具有更少的迭代次数和更短的仿真时间. 各类用户的典型用电行为规律曲线与用户负荷曲线如图3所示,图中各类用户的典型用电负荷规律曲线用黑色表示. 图3 聚类结果及各类用户用电负荷曲线Fig.3 Clustering results and load curves of various users 从图3可以看出,第一类用户整体负荷水平较高,在早晨及夜晚用电量较高,凌晨用电量较少,应为一些小型原料指向性工业,由于原料不能久贮,因此一天内大多数时间处于生产时间,比如小型水果加工厂.第二类用户整体负荷水平较低,用电主要集中在白天,午时以及夜晚用电相对较少,在6点左右有一次负荷峰值,可能为设备启动造成,而且负荷变化较快,应该存在一些非线性设备,如一些熔焊、烘焙商铺.第三类用户白天用电量较低,下午18点至凌晨1点用电量较高,由于该类负荷高峰期主要集中在夜间,负荷水平比较低,应为一些餐饮、娱乐类用户,如夜市、KTV.分析结果与甘肃武威地区实际调查结果相符合.由此可见,基于优选特征集的K-means聚类方法具有较高的准确性,可用于刻画电力用户的用电行为. 选取各群体用户的峰谷差率、峰谷差量、日平均负荷、峰时耗电比和日最大负荷数据作为基本状态数据,取各群体用户的经济情况、温度数据、用户理想电价和节假日数据作为影响因素数据,建立状态增广矩阵,利用随机矩阵理论进行分析,其分析结果如图4所示. 由图4可以看出,不同的用户对于不同的影响因素都具有不同的反映特征.第一类用户主要受经济情况影响比较多,理想电价和节假日等方面影响较小,可以看出该类用户主要受限于生产规模的大小.对于第二类用户,温度和经济情况的影响要远远高于其他几个影响因素.第三类用户对于节假日的敏感程度要高于其他两类用户,因此该类用户在节假日期间会有更多的用户.总体来说,经济情况和温度对三类用户的影响程度都较高,而理想电价相对影响程度比较低. 图4 用户行为刻画分析结果Fig.4 Analysis results of user behavior description 综上所述,电力公司在针对第一类电力用户时,要根据其经济情况来制定相应的售电方案,其挖掘潜力受限于电力用户的经济情况限制.对于第二类用户,电力公司应主要以经济情况和温度作为主要方面制定售电方案,可以为电力用户在不同季节提供不一样的用电策略.针对第三类用户,由于节假日对该用户用电行为的影响程度较高,说明该类用户用电量的大小与人流量大小有很大相关性,电力公司可以根据这方面对该类用户不同节假日、日夜峰谷期间制定相应的用电策略. 本文针对电力行业市场化改革背景下用户用电行为刻画的必要性,提出一种基于用户基本信息数据和用电特征数据相结合的用电行为刻画方法.所提方法利用随机矩阵理论在大维数据分析和数据关联性分析方面的优势,无需将原始数据矩阵分解为多个向量进行重复计算,具有较高的分析效率,分析效果较为直观.最后,通过实际应用数据算例验证结果表明,该方法能够较好地分析用户基本信息数据和用户用电行为之间的关联性,有助于售电公司对不同电力用户采取不同的售电方案和电力需求侧响应策略,提升对电力用户的服务质量,促进电力系统的高效运行.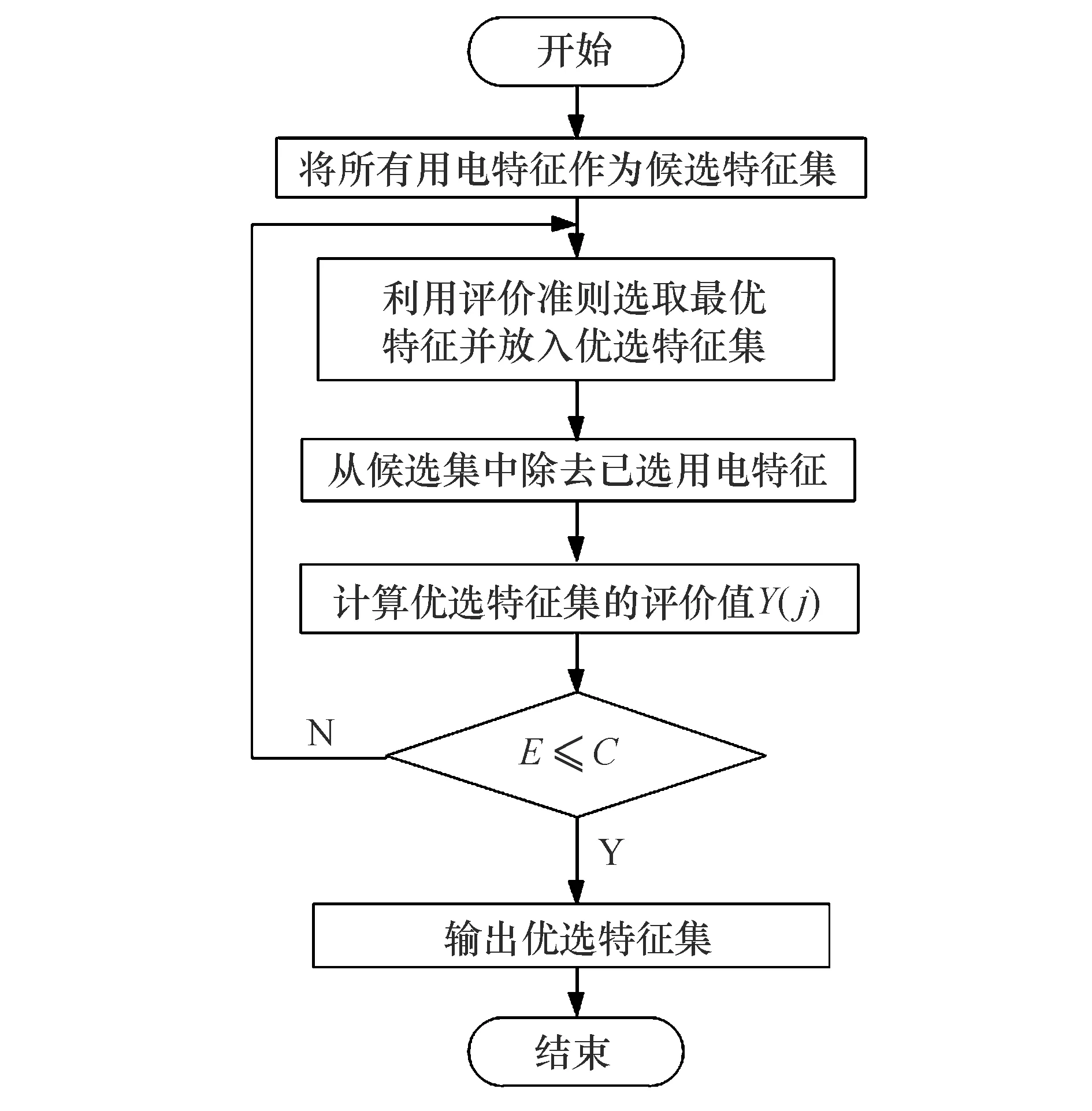
1.2 K-means聚类法
2 用户用电行为刻画方法
2.1 随机矩阵理论
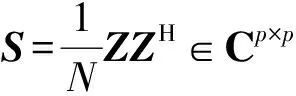
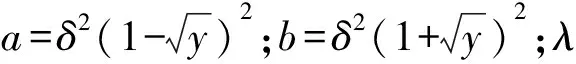
2.2 构建用户用电行为刻画模型
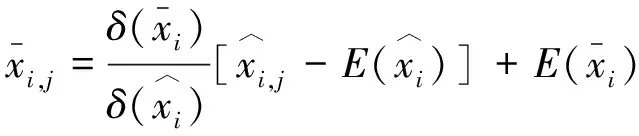
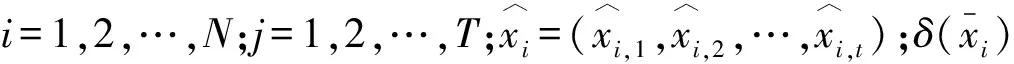
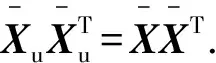
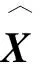
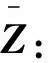
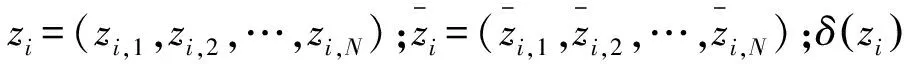
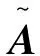
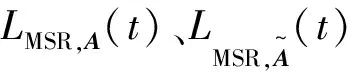
3 算例验证及分析
3.1 特征优选集的选取
3.2 用电行为聚类方法验证

3.3 用户行为刻画方法
4 结论

