基于M-WDLS和PCA的转子故障诊断方法

赵荣珍, 常书源

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

旋转机械广泛应用于机械制造、电力等许多重要领域,一旦发生故障会导致突然停机,造成重大经济损失,甚至威胁人身安全[1].转子作为旋转机械的核心部件,它的故障是造成旋转机械故障的重要原因[2].因此,对转子系统进行故障诊断具有重要的现实意义.

故障诊断本质上是故障模式辨识,而故障模式辨识的效果受制于前期的特征提取.随着数据获取和存储技术的长足发展,描述故障状态的特征维度也在不断地增加,导致在对故障状态敏感的特征中混杂了大量的冗余信息,不同故障的特征属性交互重叠,这为人工智能的模式识别带来了极大的挑战.因此,需要对高维数据进行有效的维数约简[3].

特征选择是降低数据维数的一类重要方法,能够在提供足够多分类信息的同时避免特征数目过多而引起维数灾难[4].在特征选择方法中，较典型的有Fisher分值(fisher score,FS)[5]、方差分值[6]、拉普拉斯分值(Laplacian score,LS)[7]等.其中,FS是一种监督式特征选择算法,它仅仅关注特征的区分能力,以区分能力为标准筛选特征,但没有考虑特征的局部信息保持能力.方差分值是最简单的无监督特征选择算法,它认为特征的方差越大表示能力就越强,但它只用了特征的统计特性,并没有关注数据的流形特性.LS是一种以局部保持投影[8]和拉普拉斯映射[9]为基础,结合特征的方差和局部信息保持能力来进行无监督特征选择的方法,已经被应用到生物医学[10]、故障诊断[11-12]等领域.然而,LS算法目前仍存在以下两个主要缺点：1) 在LS计算特征得分的过程中,以欧式距离为度量函数来构造特征的近邻图，但已有研究表明,在高维空间中,欧氏距离不能提供显著的相对距离差,从而无法明显体现特征之间的差别；2) LS作为无监督算法,无法利用样本中的标记信息,从而无法筛选出具有较好判别性的特征.

针对上述两点不足,本文欲通过引入Manhattan距离[13]以克服高维空间中距离的计算问题.进一步地,通过引入监督思想改进LS算法的权值函数,以充分利用样本中的标记信息来提升算法的特征筛选性能,提出基于Manhattan距离的权值判别拉普拉斯分值(manhattan-weighted discriminative laplacian score,M-WDLS)特征选择方法.

多元统计学中的主成分分析(principal component analysis,PCA)[14]可以抽取样本集的主要元素,挖掘出隐藏在复杂数据中的简单结构,不但能使数据可视化,而且能提高分类效率,被广泛应用在多个领域.因此,本文拟结合M-WDLS与PCA进行转子故障数据集的维数约简和故障诊断.首先,对转子系统振动信号在时域、频域、时频域分别提取特征,构造混合域特征集；然后用M-WDLS方法进行特征选择,形成特征矩阵；最后对特征矩阵进行PCA降维处理,并用K-近邻(K-nearest neighbor algorithm,KNN)分类器[15]来建立低维特征向量与故障类别之间的对应关系.

1 LS特征选择算法原理

LS算法的基本思想[11]是：根据局部保持能力衡量特征的重要性,特征的分值代表其保持局部结构的能力.该值越低表示其在特征空间中保持局部结构的能力越强,意味着这个特征越好.

LS假设同类样本间距离较近,异类样本间距离较远,令s个特征的LS为Ls,定义为

2 提出的M-WDLS算法

2.1 距离度量公式

由式(2)可知,LS方法采用欧式距离来衡量高维空间中特征间的相似性,从而无法有效体现特征之间的差别[3,13].然而文献[13]通过数据升维实验证明,在高维空间中Manhattan距离可提供较欧氏距离更大的相对距离差值,能够更好地体现出特征间的差异性.因此,引入Manhattan距离作为距离度量函数,即

(3)

式中：xi、xj为d维空间上的两个点.

2.2 提出的判别赋权函数

LS属于无监督方法,无法利用数据标记中的先验信息来筛选出有利于实施分类的特征.因此,将样本的类别标记信息引入权值设置,在式(2)的基础上,定义一种有监督的判别赋权函数模型：

(4)

由式(4)和图1可以看出:一方面,当自变量相同时,同类近邻点权值大于异类近邻点权值,因此同类近邻点较异类近邻点具有更高的相似度,使得同类近邻局部散度小于异类近邻局部散度;另一方面,相对于简单的权值函数权值函数模型和热核函数权值模型,判别权值函数中同类近邻点权值保持不变,异类近邻点权值变小,使得局部结构的散度也必然变小.因此从局部结构优化的角度而言,结合了标记信息的判别权值函数模型比简单的权值函数权值函数模型与热核函数权值模型更具判别性.

图1 判别权值函数图Fig.1 The graph of discriminant weight function

2.3 设计的M-WDLS算法

综上所述,本文将Manhattan距离度量和判别赋权函数结合对LS进行改进,提出一种M-WDLS方法.令Kt为第t个特征的M-WDLS,fti为第i个样本的第t个特征(i=1,2,…,l,t=1,2,…,D),其中l为样本个数,D为特征的维数.M-WDLS的具体计算步骤设计如下：

步骤1 采用式(3)度量,通过K-近邻法分别构建类内局部近邻图Gw和类间局部近邻图Gb.

步骤2 按照式(4)，根据Gw和Gb计算加权矩阵W的元素.

步骤3 对于第t个特征,定义

式中:I为l维单位矩阵,L为图的拉普拉斯矩阵.

由于某些维度数据差异很大,会主导局部近邻图的构造,所以需对各个特征进行去均值化处理

(9)

步骤4 计算第t个特征的得分

式(10)中,分子越小表示近邻样本在该特征上的差异越小,即该特征保持局部信息的能力越强；分母越大表示样本在该特征上差异越大,即该特征的区分能力越强.因此,特征重要性与其得分成反比,即特征得分越低,该特征越重要.那么，根据得分对这些特征进行升序排列,排在越前的特征越重要,M-WDLS特征选择法选取Kt值最小的前若干个特征作为特征筛选的结果.

3 M-WDLS与PCA结合的故障诊断流程

本文建立的故障诊断方法在一个典型双跨度转子实验台上进行了实验验证,故障诊断方法的流程如图2所示,该方法的使用步骤如下：

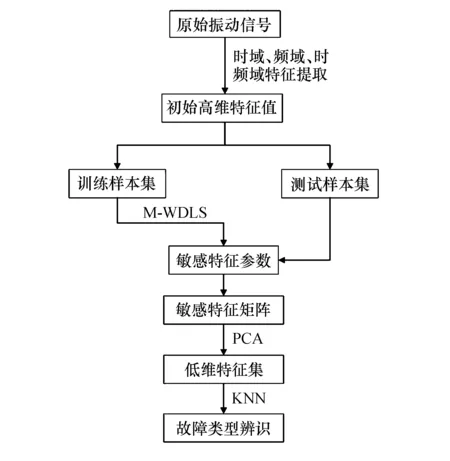
图2 基于M-WDLS和PCA故障诊断方法流程图

首先,采用文献[16]中的混合滤波方法对原始振动信号进行消噪处理,对消噪后的振动信号进行时域、频域、时频域的特征提取,得到初始高维特征集.其次,对初始高维特征集中的每一个特征计算其M-WDLS分值,按照从小到大的顺序选择若干个特征形成敏感特征子集.最后,用PCA挖掘出敏感特征子集中的主成分,并输入KNN分类器实现对转子系统故障的诊断.

4 实验结果与分析

4.1 实验数据

本研究工作的实验对象为文献[17]中的双跨度转子实验台，如图3所示.设备安装有13个电涡流传感器.其中,1个传感器布置在电机端用于采集转速信号,其余12个传感器分别布置在6个截面处的相互垂直方位,用于采集不同方位的振动信号.在该设备上分别模拟转子不对中、质量不平衡、动静碰磨、轴承松动及正常转动5种状态实验.设置采样频率为5 000 Hz,转速为3 000 r/min,采集各种状态类型数据样本80组,其中20组作为训练样本,60组作为测试样本.对每个通道采集的信号按表1所列的参数提取特征,扩展至12个通道,构造12×26=312维的混合域特征集,特征集构造方式如表2所列.

图3 双跨度转子实验台Fig.3 Double-span rotor test bench

表1 特征参数Tab.1 Characteristic parameters

表2 初始高维特征集Tab.2 Initial high dimensional feature set

… ,f400,n]T,(m=1,… ,400;n=1,…,312).

4.2 相关参数选取

按照图2所示的流程,本文需确定的参数有：M-WDLS中的近邻参数k1与选择敏感特征向量的数量m,PCA降维的目标维数d及KNN中的近邻参数k2.

其中,PCA降维的目标维数d采用极大似然估计法计算得到d=4.不同的k1与m组合得到的效果在KNN中的识别率不同,设置k1的范围为3～15,步长为1.用M-WDLS计算各个特征量的得分,剔除得分大于0.1的特征量,剩余的特征量作为候选特征.经多次试验,确定的40个候选特征量={F288,F301,F287,F290,F289,F184,F183,F186,F185,F197,F262,F261,F264,F263,F236,F275,F238,F235,F237,F249,F93,F157,F1,F48,F80,F85,F276,F269,F149,F76,F82,F267,F60,F266,F279,F69,F58,F94,F81,F281}，因而选定m的范围为4～40,步长为1.对所有的k1和m进行计算,结果如图4所示.

由图4可知,当k1=8时,整体识别率相较于其他情况更好,尽管k1取其他值时也有识别率较高的情况出现,但起伏较大不稳定,整体而言k1=8时效果最好.当k1=8,m的范围为17～20时,整体识别率达到最大值99%.固定单一分量k1=8,参数m的选择情况，如图5所示.

图4 整体识别率随k1与m的变化Fig.4 The overall recognition rate change with k1 and m

由图5可以看出,当k1=8时,m在17～20范围内整体识别率达到最高,但从21开始整体识别率有所下降.由此表明特征量个数m对故障诊断结果有显著影响,若特征量个数过少,则无法完全反映和区分故障类型与故障程度,诊断精度不高；如果特征量个数过多会造成信息的冗余,降低诊断精度.基于上述分析,选择特征量个数过多或过少都不宜，本文选取m=18是可行且合理的.因此选择出的18个特征向量={F288,F301,F287,F290,F289,F184,F183,F186,F185,F197,F262,F261,F264,F263,F236,F275,F238,F235}.

图5 k1=8时整体识别率随m变化曲线Fig.5 The overall recognition rate change with k1 and m

确定k1和m的取值后,将经PCA降维得到的低维特征集输入到 KNN中,并设置k2的范围为3～15,其整体识别率随k2变化如图6所示.可见当k2=6时,KNN达到了最高识别率.

图6 整体识别率随k2变化的曲线Fig.6 The overall recognition rate change with k2

通过上述分析可以看出,当k1=8、m=18、k2=6时,整体识别率能达到较为理想的效果,因此本文在实验分析中采用这些取值.

4.3 确定的评估方法

为进一步说明本文方法的有效性,采用文献[2]中类间离散度与类内离散度的相关比值Je作为评价指标进行算法的有效性评估.Je越大,则说明类内离散度越小,类间离散度越大,分离效果越好.Je的计算公式如下：

(13)

(14)

(15)

4.4 结果分析

为验证本文提出方法的有效性,分别用FS、LS、SLS算法代替2.3节所示流程中的M-WDLS算法,对高维特征集进行特征筛选,对比4种方法的诊断效果.经4种算法筛选后得到能使识别率达到最高的最优特征子集如表3所列.4种算法筛选出的最优特征子集经PCA降维可视化得到的三维输出效果如图7所示.用评价指标Je评价图7中基于4种方法的分离效果,结果如表4所列.

表3 各个算法选择出的特征子集Tab.3 Feature vector selected by each algorithm

表4 四种方法类间类内评价指标Tab.4 Four methods and inter-class evaluation indicators

由图7和表4可以看出:图7a和图7b中转子不对中、松动、碰磨这3类故障分离,但是质量不平衡与正常状态之间存在不同程度的混叠,而且FS与LS两种方法筛选出的特征分类评价指标都较低,说明类间并没有很好地分开,这是由于经FS与LS筛选后的特征集中还存在冗余数据；图7c中SLS筛选出特征的分离效果较FS和LS好,5种状态大致分离,但不平衡、碰磨、正常这3类状态之间间距较小,类间离散度小,其评价指标Je=9.773 4,亦可佐证这点；图7d中故障状态分离效果最好,明显使类内聚集、类间分离,评价指标Je达到15.670 7,可见M-WDLS能有效筛选出对故障敏感且聚类性较好的特征,具有一定的优越性.

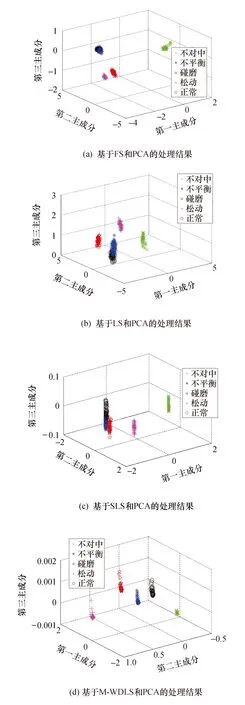
图7 测试样本基于不同算法的可视化效果

将上述4种方法得到的融合特征集分别输入KNN分类器.为了对比,同样将特征集输入SVM分类器，进行故障辨识,SVM选用RBF核函数,设置惩罚参数C=1,核参数ε=1，结果如表5所列.

表5 特征选择算法及其KNN辨识准确率Tab.5 Feature selection algorithm and its KNN identification accuracy

由表5可知:原始特征的分类精度远低于特征选择方法筛选出特征的分类精度,这表明了特征选择的重要性；并且KNN的平均辨识精度优于SVM的.

分析表3和表5可知:从最优特征子集来看,本文方法在所有特征选择方法中得到了最小的特征子集规模,而其他3种方法得到的特征子集维数均略大；从分类准确率方面来看,基于M-WDLS算法的分类精度最高为99%,具有一定优势.

为进一步验证本文所提方法的稳定性,改变训练样本与测试样本的比例,设置训练样本数/测试样本数为10/70、15/65、20/60、25/55、30/50、35/45、40/40、45/35、50/30.并且分析出4种方法的低维测试样本输入KNN分类器所得的平均识别率,如图8所示.

图8表明:总体上,4种特征选择方法的平均识别率都随训练样本数的增加而增加,这是因为训练样本越多,其中所包含的判别信息就越多,所以故障识别率得到了一定提升；LS方法在训练样本少于25时平均识别率出现波动情况,这是由于LS并不能有效提取存在于数据样本中的判别信息；SLS的稳定性和平均识别率明显优于FS与LS,但在训练样本较少时,识别率低于M-WDLS；其中,M-WDLS的稳定性最好,在训练样本较少的情况下也能取得较好的平均识别率,明显优于其他3种方法.

图8 不同训练样本数对应的平均识别准确率Fig.8 The average recognition accuracy of different training sample

以上分析表明,基于M-WDLS特征选择方法能够有效地提取转子故障的特征信息,与PCA及KNN分类器结合可以有效实现转子系统的故障诊断,比基于FS、LS、SLS的方法具有更好的辨识精度和稳定性,是一种有效的转子故障诊断方法.

5 结论

本文提出一种M-WDLS特征选择算法,该算法使用Manhattan距离作为度量函数量化样本间的相似性.在考虑数据局部几何结构的同时,将数据的标记信息融入权值的设置,充分利用了数据的标记信息,使算法能有效提取对故障敏感的特征,减少无关或冗余特征.方法的验证结果表明,用M-WDLS方法进行特征选择得到敏感特征矩阵,再对敏感特征矩阵进行PCA降维处理,能有效提取转子系统故障特征.在此基础上再应用KNN分类算法对转子系统故障状态进行识别,能有效地提高转子系统故障辩识的准确性.