基于矩阵分解的算法在微生物疾病关系预测中的应用探析
杨 杰
(西南民族大学数学学院,四川 成都 610041)
在自然界中广泛存在的细菌、真菌和病毒等微生物与人类生活和人体健康密切相关,与人类有关的微生物分布在人体的口、鼻、皮肤、胃肠道和泌尿生殖道等各部位[1].伴随人类基因组计划的完成,科学家们提出了进一步了解微生物群如何影响人类健康和疾病的人类微生物组计划(Human Microbiome Project,HMP)[2],以更进一步探究人类基因、人体内微生物组、人类疾病和药物疗效等间的关系,已有研究证明微生物与人类代谢疾病、糖尿病、炎症性肠病、肥胖症和癌症等密切相关[3].按照传统的生物实验方法发现微生物和疾病之间的关系,往往实验成本高的同时周期也长.根据己知的实验验证的微生物和疾病关联数据,采用计算方法预测潜在的致病微生物关联关系能为生物实验提供实验方向,降低实验成本减少实验时间,也有助于研究微生物对疾病的发生、发展和药物治疗的关系.近年来,基于已知的微生物和疾病关系数据集,研究人员提出了越来越多的预测微生物与疾病的计算方法,例如基于KATZ方法的KATZHMDA[4]、基于路径的PBHMDA[5]、基于随机游走的PRWHMDA[6]、基于机器学习的LRLSHMDA[7]和基于元图的WMGHMDA[8]等算法.矩阵分解是推荐系统中的常用模型,本文重点对矩阵分解算法中的非负矩阵分解算法原理、Logistic矩阵分解原理在疾病和微生物关系预测的应用做了分析,并对矩阵分解在在疾病相关微生物关系预测方面的应用作了展望.
1 数据集
在疾病-微生物关联关系预测中离不开相关的数据库,常见的微生物和人类疾病相关的数据库包括eHOMD[9]、HPMCD[10]、HMDAD[11]和MorCVD[12]等数据库.eHOMD数据库提高鼻腔、鼻窦、口腔、咽和食道等人类呼吸消化道中的775种微生物、2 074个口/鼻基因组和包括非口腔/非鼻类群总数为2 087基因组的相关数据,同时eHOMD基于16S rRNA序列系统发育为当前未命名的微生物分类群提供了一种临时命名方案参考方案.HPMCD数据库可提供人类1 800多个人类胃肠道基因组样本相关的微生物群检索、功能检索、序列检索和微生物群注释服务,该数据库的建立极大方便了微生物学研究人员、基于临床和疾病的研究人员以及基于遗传学和基因组学的研究人员的相关研究.HMDAD数据库包括292种微生物、39种人类疾病和483种微生物人类疾病关联关系,数据库中的数据是从2014年7月之前发表的人类微生物组文献中收集、整理而来可供用户搜索、浏览和下载(http://www.cuilab.cn/hmdad).MorCVD是一个涵盖心肌炎、心包炎和心内膜炎以及由微生物引起的其它16种心血管疾病的总计23 377个宿主-病原蛋白质互作关系(HPPPI)及其相关参考文献的数据库.研究者可方便在数据库中检索病原体名称、蛋白质和宿主蛋白质,检索基因ID和基因本体ID,检索相互作用物、相互作用类型、HPPPI的相互作用和药物靶点等.在疾病相关微生预测中用得较多的一个数据库是HMDAD数据库.
2 矩阵分解算法
数学中的矩阵分解通常是指一个矩阵分解成多个矩阵相乘的过程.矩阵分解的思想已经在推荐系统、链路预测、生物信息学和金融统计等领域得到了应用,常见的矩阵分解方法包括奇异值分解(Singular Value Decomposition,SVD)[13]、非负矩阵分解(Nonnegative Matrix Factorization,NMF)[14]和概率矩阵分解(Probabilistic Matrix Factorization,PMF)[15]等.
SVD分解原理可简单表述为给定一个矩阵Rm×n可分解成R=US VT的形式,其中Um×r和Vn×r为正交矩阵,Sr×r为R的所有为正且从大到小排列得奇异值组成的对角矩阵.文献[13]作者在推荐系统中引入了SVD技术用于初始评分矩阵的降维,发现用户和项目的潜在关系.
NMF技术是一种与PCA和VQ等方法不同,把一个非负的矩阵分解成两个低秩非负矩阵,采用非负约束的矩阵分解方法.NMF及其改进算法由于具有全局和局部兼顾、可解释性强和应用简单等特性,在图像识别和数据挖掘等领域得到了广泛应用.对一个非负的矩阵X+∈Rm×n可分解成两个非负的矩阵U+∈Rm×k和V+∈Rk×n,其中k<min{m,n},E表示误差或残差,则标准的NMF和欧氏距离优化模型可表示为[14]:

标准的NMF仅适用于非负数据,限制了NMF的应用,文献[16]作者在标准的NMF的基础上移除对矩阵X和U的非负限制,扩展成了半非负矩阵分解算法Semi-NMF,表示如下:

标准的NMF和Semi-NMF存在尺度方差和非唯一解问题,导致约束在最小二乘上的非负性是在某些情况下不适合.为增强NMF的可解释性,结合统计建模中的稀疏正则化原则,文献[17]作者提出了Sparse-NMF,表示如下:

文献[18]作者提出了图正则化非负矩阵分解GNMF,其最小化目标函数可表示为[18-19]:

公式(5)中,tr(·)表示矩阵的迹,L=D-S为拉普拉斯矩阵,D是对角矩阵且,样本邻接图的构建可表示为:

概率矩阵分解模型由文献[15]的作者于2007年提出.PMF模型为推荐系统中矩阵分解提出了概率解释.在PMF的基础上,多种概率矩阵分解模型相继提出,例如贝叶斯概率矩阵分解模型和Logistic矩阵分解模型(Logistic Matrix Factorization,Logistic MF)[20]等.Logistic MF模型在推荐系统中没有采用RMSE作为损失函数而是采用概率方式作为损失函数,具体描述如下:
若U=(u1,…,un)表示用户,I=(i1,…,im)表示物品,R=(rui)n×m表示用户物品联系矩阵.若给定观察矩阵R,则R可通过两个低秩矩阵Xn×f和Ym×f近似表示.lui表示用户u选择物品i的事件,βi代表用户偏置,βj代表物品的偏置,则条件概率可表示为:

用置信度表示频率的置信映射函数可表示为:
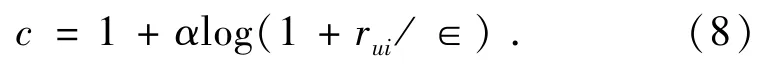
若R的所有元素都独立,则给定参数X,Y和β,由公式(7)和(8)有

此外,为由利于正则化和避免过拟合,设用户和物品的隐因子向量服从零均值球形高斯先验分布:
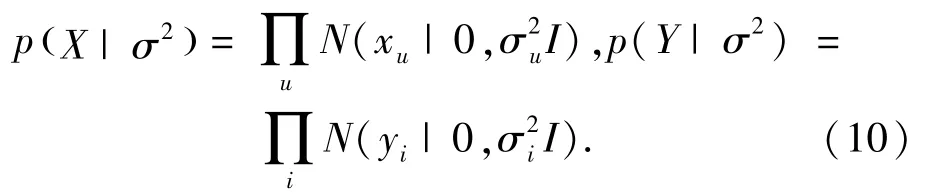
取对数后验概率并用平滑参数λ替换常数项得:

后验概率最大化:

可以对(12)采用交替梯度下降优化.求用户向量和偏差的偏导数公式,如(13)和(14)表示:

迭代公式如公式(15)表示:

3 矩阵分解算法在疾病相关微生物预测中的应用
文献[21]作者提出了一种矩阵分解和标签传播融合的微生物疾病关系预测算法MDLPHMDA.在矩阵分解部分MDLPHMDA把原始的邻接矩阵A分解成A=AX+E的形式,其中X是低秩矩阵,E是稀疏矩阵.通过系列优化问题求解最终得到一个新邻接矩阵A*和新的低秩矩阵X*的求解等式A*=A X*.MDLPHMDA在HMDAD数据集上确定了LOOCV下的AUC值为0.9034.
文献[22]作者提出了一种称为MCHMDA的低秩矩阵补全方法.该方法的数据处理部分首先基于HMDAD数据库中的微生物-疾病关联关系采用高斯相互作用谱(Gaussian Interaction Profile,GIP)核函数分别计算计算微生物和疾病的GIP相似性,其次基于微生物是否栖息于同一类器官加权调整微生物的GIP核相似性最终得到用于算法的微生物相似性,同时根据疾病相关的基因计算疾病的功能相似性,最后把疾病功能相似性、疾病症状相似性和疾病GIP相似性融合取均值得到最终的疾病基本相似性.该方法再算法部分首先方法采用KNN算法初始化未知联系的微生物-疾病关联矩阵得到新的微生物-疾病关联矩阵,再把微生物相似性、疾病相似性和新的微生物-疾病关系整合到异构网络通过快速奇异值阈值(Singular Value Thresholding,SVT)算法,使用矩阵补全方法计算未知微生物-疾病对的关联分数,从而预测未知的疾病关联的微生物.MCHMDA的SVT算法中采用了SVD分解来选择奇异值和奇异向量.
文献[23]作者提出了名为GRNMFHMDA的人类微生物疾病关联预测的图正则化非负矩阵分解模型.该模型可分为三个步骤:①数据准备阶段基于HMNDAD数据库建立微生物和疾病邻接矩阵,分别计算微生物和疾病的GIP相似性,融合疾病症状相似性得到集成的疾病相似性,②预处理阶段基于微生物GIP相似性集成的疾病相似性和已知关联的疾病微生物关系分别采用加权K最近邻算法计算微生物和疾病的新的互作谱后计算未知的微生物-疾病关系的相关似然分并更新关联矩阵;③在标准NMF框架中引入Tikhonov(L2)和Graph Laplacian正则化,得到最终的分数矩阵,从而预测疾病关联的微生物.预测性能上全局LOOCV取得的AUC值 为0.8715,局部的LOOCV取得的AUC值 为0.7898.同理,文献[24]作者采用采用类似算法在五折交叉验证取得了AUC值为0.8891的性能.
文献[25]作者提出了基于logistic矩阵分解预测潜在可能的人类疾病关联的微生物的方法RNMFMDA.基于HMNDAD数据库中已知的微生物和疾病关联(Microbe-Disease Association,MDA),先分别计算微生物和疾病的GAP相似性,再把疾病GAP相似性和疾病语义相似性加权融合的得到新的疾病相似性.通常高质量的负样本MDA可以提升预测模型的性能,大多数已知方法都是随机从未知的微生物-疾病关联中选择负样本,但此类选择随机选择负样本的方法可能包含正样本从而影响算法性能.鉴于HMNDAD中无副样本MDA,此文献先提出了一种基于重启随机游走算法计算微生物-疾病关联对概率和基于PU学习提取高质量负MDA样本的方法,受文献[26]和文献[27]的启发,RNMFMDA在前面步骤的基础上集合logistic矩阵分解实现了对潜在可能的人类疾病关联的微生物预测.
文献[28]作者提出了一种基于神经网络使用贝叶斯个性化排序的深度矩阵分解算法DMFMDA,该算法矩阵分解部分采用one-hot编码疾病和微生物,作为神经网络输入,通过嵌入层将其转化为隐语义空间的低维密度向量,再通过带有嵌入层的神经网络实现矩阵分解.DMFMDA基于矩阵分解的线性建模优势集合了多层感知器的非线性建模优势,在五折交叉验证和LOOCV下分的AUC值分别为0.9091和0.9103.
4 结论
低秩矩阵分解、SVD分解、概率矩阵和非负矩阵分解等相关矩阵分解算法在疾病相关微生物预测中已经得到了应用,但大多数单一矩阵分解算法在数据及其稀疏和单一的情况下可能预测效果达不到理想的效果.微生物和疾病网络本质上属于复杂网络,网络节点本身具有多重属性性质,结合目前图神经网络和图注意力网络相关研究热点的兴起,在疾病相关的微生物预测方面可考虑引入融合多元信息异构网络上的图神经网络和图注意力方面的算法进行矩阵分解的相关研究.

