高速移动通信系统中OTFS信道估计算法研究
蒋占军 刘庆达
(兰州交通大学电子与信息工程学院 兰州 730070)
1 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)调制方案已广泛应用于现代无线通信系统中,但对于时变信道,例如高速铁路无线通信信道,较大的多普勒效应和丰富的多径效应会导致信道频率色散和时间色散,破坏子载波之间的正交性,从而可能遭受严重的子载波间干扰(Inter-Carrier Interference,ICI),当采用传统发射接收机时,ICI使时域和频域的维纳滤波器相关函数不再精确,进而影响信道估计的准确性[1,2]。针对上述问题,目前的解决办法是对发射机和接收机进行优化,对于接收机的ICI,通常使用复杂度较高的线性均衡[3–6]技术和非线性均衡[7–9]技术加以消除,对于发射机的ICI则经常使用多项式抵消编码[10,11]和脉冲整形[12,13]技术进行处理。
除了尝试减小ICI的方法之外,还有一些针对时变信道的调制方案,例如利用发射分集来增强系统性能,从而提高信道估计的准确性。文献[14]提出了一种用于零填充OFDM系统的频率过采样技术,该技术可以通过设计发射信号来实现频率分集。Vector OFDM技术在信道子载波上传输多组线性预编码符号,以提供频率分集[15]。多普勒弹性正交信号划分多路复用技术将多个数据矢量和导频矢量多路复用到数据流中,以充分利用时变信道中的频率-时间分集[16,17]。
与OFDM相比,正交时频空(Orthogonal Time Frequency Space,OTFS)调制系统通过一系列的2维变换,将双色散信道转换为时延多普勒域中时不变的2维信道,并在时延多普勒域中复用数据,因此原有OFDM系统在时频域中的信道估计算法也需要做相应改进。基于正交匹配追踪(Orthogonal Matching Pursuit,OMP)的信道估计算法根据导频序列的输入输出关系将OTFS系统的信道估计问题转化为压缩感知问题[18,19],通过稀疏向量中非零值元素及其对应位置,估计信道增益、时延、多普勒频移等信道参数[20]。该方案具有较高的信道估计准确度,但导频所占资源较大,为此,本文设计了一种节省导频资源的正交匹配追踪(Pilot Resource Saving-Orthogonal Matching Pursuit,PRS-OMP)信道估计算法,并在其基础上,通过提高OTFS调制系统的分集阶数,进一步提升信道估计的准确性和系统误码率性能。
2 OTFS系统结构模型
单输入单输出 OTFS(Single Input Single Output OTFS,SISO-OTFS)系统框图如图1所示,该系统发送和接收未编码的调制符号,可以将其视为在传统OFDM系统中增加了前置处理模块和后置处理模块的实现方案。其中前置处理模块为辛傅里叶逆变换(Inverse Symmetric Finite Fourier Transform,ISFFT),后置处理模块为辛傅里叶变换(Symmetric Finite Fourier Transform,SFFT)。

图1 OTFS系统框图
首先,在发送端,将MN个数据信息符号摆放至时延-多普勒域信号网格中,其中多普勒域中有N行数据,时延域中有M列数据;然后,通过ISFFT将时延-多普勒域信号变换到时频域,如式(1)所示

时频域信号经过海森堡变换(Heisenberg transform)后成为时域信号。在接收端,时域接收信号由维格纳(Wigner)变换成为时频域信号,经过SFFT处理解调得到时延-多普勒域的数据,如式(2)所示

由OTFS系统调制解调相关变换可得OTFS系统输入输出关系为
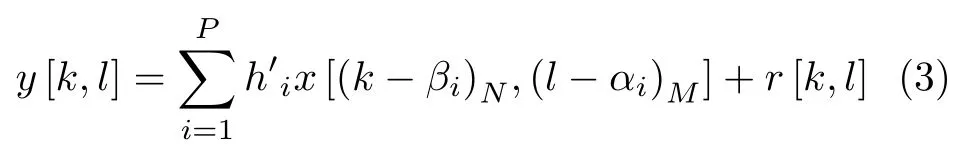
其中,n=(k-βi)N表示(k-βi-n)能被N整除时k的取值,m=(l-αi)M表示(l-αi-m)能被M整除时l的取值。其中τi=αi/MΔf υi=βi/NT,τi表示时延量,υi表 示多普勒频移量;M为子载波的个数,N为一帧符号的个数;r[k,l]表示时延多普勒域中的噪声;hi表 示信道幅度增益,信道增益为
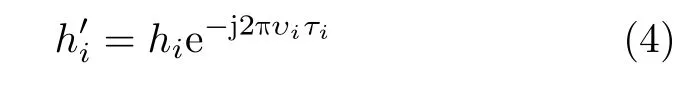
3 导频资源节省的OMP算法(PRS-OMP)
3.1 算法理论分析
在式(3)给出的SISO-OTFS输入输出关系的基础上,令导频符号单独成帧作为发送信号,将其用矩阵形式重写为


当路径数量P=MpNp时,矩阵Xp是具有循环块的块循环矩阵,如式(7)所示,Xp具有Mp个循环块,每个循环块的大小为Np×Np,通过循环移位以形成块循环矩阵。在式(7)中,表示第l块 的第q个元素,其中q=0,...,Np-1并 且l=0,...,Mp-1。

由式(5)可以看出,此时,对于OTFS系统信道参数的估计问题就转化为了对接收序列向量的分解问题,即求Xp的系数的问题。由此得到PRS-OMP信道估计算法的步骤如表1所示。

表1 本文PRS-OMP信道估计算法步骤

3.2 仿真分析
如图2所示,本文针对3个不同OTFS系统在经过PRS-OMP信道估计及文献[20]中的OMP信道估计后分别进行误码率性能分析,3个系统参数由表2列出。多普勒频移依据Jakes公式随机生成:vi=vmaxcos(θi),vmax代表移动最大速度,θi在[-π,π]均匀分布。
表2中M,N的取值方法为:首先,根据最大速度能够求出最大多普勒频移;通过确定最大时延τmax和最大多普勒频移υmax并设计好一帧符号的时间Tl;若要减小多普勒频移和时延扩展的干扰,须要满足υmax<Δf <1/τmax,以此确定子载波间隔Δf。然后,根据带宽B和Δf确定子载波的个数M,取M=B/Δf,再根据Tl和Δf确定符号的个数N,取N=TlΔf。表中3个系统的子载波间隔均为3.75 kHz,最大时延统一是1/7500 s;系统1和系统2的最大多普勒频移为1.875 kHz,系统3的最大多普勒频移为0.9375 kHz。经过计算系统1~3的(MP,NP)分别为(2,2),(3,2)和(3,2)。
由图2中3个系统BER曲线可以发现,增大OTFS数据帧的大小可以提高BER性能。另外系统3的BER下限远低于系统1和系统2的下限,并且系统3的BER曲线以更大的斜率下降以满足其下限;此外,3个系统仿真结果和表2都表明,PRS-OMP信道估计算法可以在保证相似信道估计准确度的前提下,利用更少的导频符号估计信道参数;最后,发现3个系统渐进分集阶数均为1,所以本文将通过提高系统的分集阶数来提高信道估计的准确性和改善误码率性能。

表2 仿真参数设置

图2 两种信道估计算法下OTFS BER性能对比
4 相位旋转的PRS-OMP算法
4.1 相位旋转理论分析
为了分析出OTFS系统分集特性,将由式(3)得到的数据发送矩阵Xi中的符号做归一化处理,使符号平均功率为1。Xi经过时延多普勒信道后解调检测得到Xj,Xi和Xj是一一对应关系。文献[22]指出Xi和Xj之间的成对错误概率(Pairwise Error Probability,PEP)为

其中,信噪比ζ=1/N0,N0为噪声单边功率谱密度。λl为Δij=(Xi-Xj)的秩。信道增益h′服 从CN(0,1/P)分布,P为路径的个数。高信噪比下,式(9)可以简化为式(10)
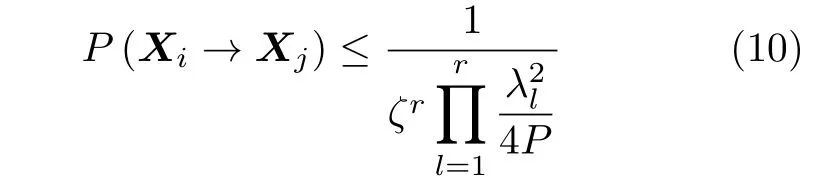
其中,SNR项ζ的指数为r,也就是差矩阵Δij的秩。对于所有ij,i/=j时,总误码率(BER)由r为最小值的PEP决定。因此,由ρ表示的单输入单输出的OTFS分集阶数为

其中,Δij=(Xi-Xj)秩的最小值为1,因此,带有ML检测的OTFS系统的渐近分集阶数为1。
当使用BPSK调制,最大似然法检测(Maximum Likelihood,ML)时,通过对满足差分矩阵Δij=(Xi-Xj)秩等于1的Xi和Xj所对应的PEP进行求和,得到了误码率的下界
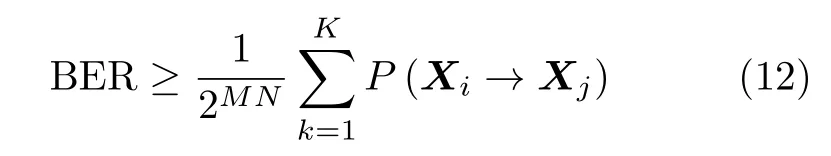
其中,K为Δij秩为1的数量。当Δij有秩为1时,它只有一个非零奇异值(λ1),可以计算为。代入文献[18]中式(29),PEP可以简化为


将式(14)代入式(12),得到OTFS系统BER的下限[22]
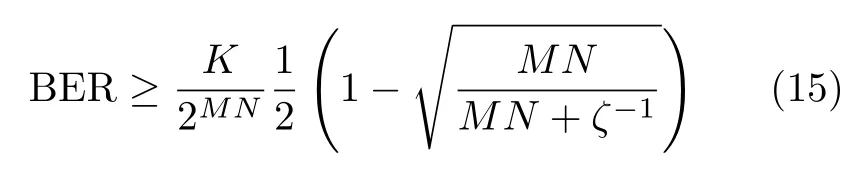
需要说明的是,若要式(15)等号成立,则式(12)等号也须成立。式(12)由式(10)和式(11)得出。当式(10)中信噪比ζ很大时,秩r的增大会使式(10)取值更小,也就是秩较大时对BER的影响将会更小,此时,总误码率(BER)将由r为最小值时的PEP所决定,从而,式(12)和式(15)在高信噪比时等号成立。
因为OTFS系统的分集阶数取决于在所有符号矩阵对差分矩阵Δij=(Xi-Xj)的最小秩,所以本文利用一种相位旋转方案增大差分矩阵的最小秩来提高系统的分集阶数,从而降低信道的噪声干扰,提高信道估计的准确度和改善误码率性能。


通过林登曼定理(Lindenmann)[23],可以得到式(23)。该定理指出,如果a1,a2,...,am是不同的代数数,并且c1,c2,...,cm是代数数且不全为零,则

4.2 仿真分析
为了评估相位旋转前后的信道估计的准确度,本文通过MATLAB仿真得到信道估计参数的均方误差(MSE)和系统误码率(BER)。图3给出了不同导频开销约束下经过相位旋转和未经过相位旋转的OTFS系统的信道估计MSE曲线,信噪比都取20 dB。可以发现本文利用的经过相位旋转的PRSOMP信道估计方案在所有导频开销下都优于未经过相位旋转之前的方案,这是因为经过相位旋转的信道估计方案能降低信道的噪声干扰,从而提高了信道估计的准确度。

图3 相位旋转前后不同导频开销下的MSE
图4为3个不同的OTFS系统在相位旋转前后误码率随信噪比变化曲线,3个系统参数如表2所示。3 个系统都使用相同的相位旋转矩阵Φ=diag。

图4 OTFS系统相位旋转前后误码率性能对比
从图4观察到3个没有经过相位旋转的系统的分集阶数是1,经过相位旋转的OTFS系统分集阶数为P=4,3个OTFS系统经过相位旋转后显著改善了误码率性能。最后通过比较发现,随着一帧符号数目的增加,虽然误码率性能得到改善,但信噪比相同时经过相位旋转后误码率改善的程度会降低,这是因为不同系统的编码增益不同,因此可以优化相位旋转矩阵中的相位,进一步提高系统实现的编码增益。
5 结束语
本文在OMP算法基础上,提出降低导频占用资源的OTFS信道估计算法PRS-OMP。该算法通过综合考虑双色散信道中最大时延和最大多普勒频移,利用压缩感知原理估算各个路径的时延、多普勒频移和信道增益。最后利用一种OTFS相位旋转方案通过提高差矩阵的秩对PRS-OMP算法进行优化。仿真结果表明,经过相位旋转的PRS-OMP算法提高了信道估计准确度和分集阶数,改善了系统误码率性能。然而,本文的仿真环境设置较为理想化,只考虑了整数多普勒频移,未考虑分数多普勒频移对OTFS信道估计性能的影响,下一步可对分数多普勒频移影响下的OTFS信道估计进行研究,并扩展至MIMO系统中上下行链路的信道估计。

