稀疏码多址接入多用户检测算法综述
雷 菁 王水琴* 黄 巍 彭小洹
①(国防科技大学电子科学学院 长沙 410073)
②(陆装驻成都地区第二军代室 成都 610031)
1 引言
面向2030年的第6代(Sixth Generation,6G)移动通信已经展开了研究。与第5代(Fifth Generation,5G)移动通信相比,6G具有更高的频谱效率和更大的系统容量,传统的正交多址技术(Orthogonal Multiple Access,OMA)已经无法满足需求[1–3]。非正交多址接入技术(Non-Orthogonal Multiple Access,NOMA)通过在发送端允许多用户共享相同的时频空资源,在接收端进行多用户检测,能有效地提高系统吞吐量和接入用户数,被认为是未来6G系统的关键技术之一[4,5]。
稀疏码多址接入(Sparse Code Multiple Access,SCMA)作为NOMA的典型代表,最早由Nikopour等人在低密度签名(Low Density Signature,LDS)[6]基础上提出。与LDS不同的是,SCMA将LDS编码过程中的正交幅度调制和扩频步骤融合,使得二进制比特流被直接编码为特定的多维复数码字[7]。由于码字的稀疏特性,在接收端可以利用消息传递算法(Message Passing Algorithm,MPA)来进行多用户检测[8,9]。相比于LDS,SCMA多维码字的设计可以使其获得成型增益和编码增益[10–14],具有接入用户数多[15]、频谱效率高[16]、延时低[17]等特点,受到了工业界和学术界的广泛关注。
SCMA系统通过码字非正交接入的方式虽然可以接入更多的用户,但也因此带来了严重的多址干扰,限制了SCMA系统的频谱利用率和容量。传统的单用户检测仅仅利用用户本身的相关性来恢复数据,其他用户多址干扰中的有用信息没有被充分利用,因此检测效率不佳。相比而言,多用户检测采用联合检测的方式弥补了单用户检测的不足,有效地改善了系统检测性能[18],成为SCMA系统接收端检测的关键技术。
SCMA多用户检测是指利用多用户检测算法对接收端叠加的信号进行分离以得到各用户码字。Verdu[19]证明最优的多用户检测算法为最大似然(Maximum Likelihood,ML)算法,在独立同分布下ML算法等价于最大后验概率(Maximum A Posteriori,MAP)算法。MAP算法通过找到后验概率最大的码字组合作为输入的用户码字,可以使用户信息被错误检测的概率最小化。虽然相比于传统单用户检测算法,MAP算法可以带来显著的性能和容量增益,但其复杂度会随用户数指数增长,实际系统难以实现。由此,学者致力于研究次优的多用户检测算法,常用的有解相关[20]、最小均方误差[21]等线性检测算法和串行干扰消除[22]、消息传递算法[9]等非线性检测算法。
由于SCMA码字的稀疏性,接收端一般采用MPA算法来进行多用户检测。MPA算法是一种置信度传播算法,通过沿着因子图上的边缘迭代地传递消息直到算法收敛或达到最大迭代次数,可以有效地提高SCMA系统检测性能和接入用户数。相比于MAP算法,MPA算法具有以下优势:(1)避免了在所有码本空间中搜索后验概率最大的码字组合,极大地降低了复杂度;(2)利用用户与资源之间的多次消息迭代更新,可以有效地对多用户消息进行分离,显著地降低了错误检测概率。尽管MPA算法具有上述优势,但当系统用户数增大时,其复杂度仍呈指数增长,限制了SCMA的实际应用。由此,设计低复杂度的SCMA多用户检测算法至关重要。近年来,低复杂度多用户检测算法成为多址接入领域的研究热点之一,目前已有大量的研究成果。
为便于读者了解SCMA检测算法的研究现状,掌握SCMA检测算法的改进思路,本文的主要工作是对SCMA现有低复杂度多用户检测算法进行较为详细的综述,并对几种典型算法进行原理剖析和性能对比。另外,为便于读者把握SCMA检测算法未来的研究方向和面临的挑战,本文将总结和探讨SCMA检测算法的发展趋势及存在的问题。
2 SCMA 系统模型
2.1 上行SCMA系统
假定J个用户共享K个正交时频资源,并向同一基站传输数据,简化的SCMA上行链路模型如图1所示。对应的过载因子定义为:λ=J/K(J>K)。SCMA编码时,各用户根据预先分配好的码本将每log2M个输入的二进制比特编码成一个K维复数码字,其中M为码本大小。该码字只有N ≪K元素为非零值,从而保证了码字的稀疏性,以便于接收端进行多用户检测。以J=6 用户K=4资源SCMA系统为例,对应的编码映射过程如图2所示,每个码本有4个码字,每个码字有2个非0元素(图2中非空白方框表示),用户1—用户6发送的比特数据00,01,11,10,00,01分别被编码成对应用户码本的第1,2,3,4,1,2个码字。用户和资源的关系可以用因子矩阵F表示,F的维度为K×J

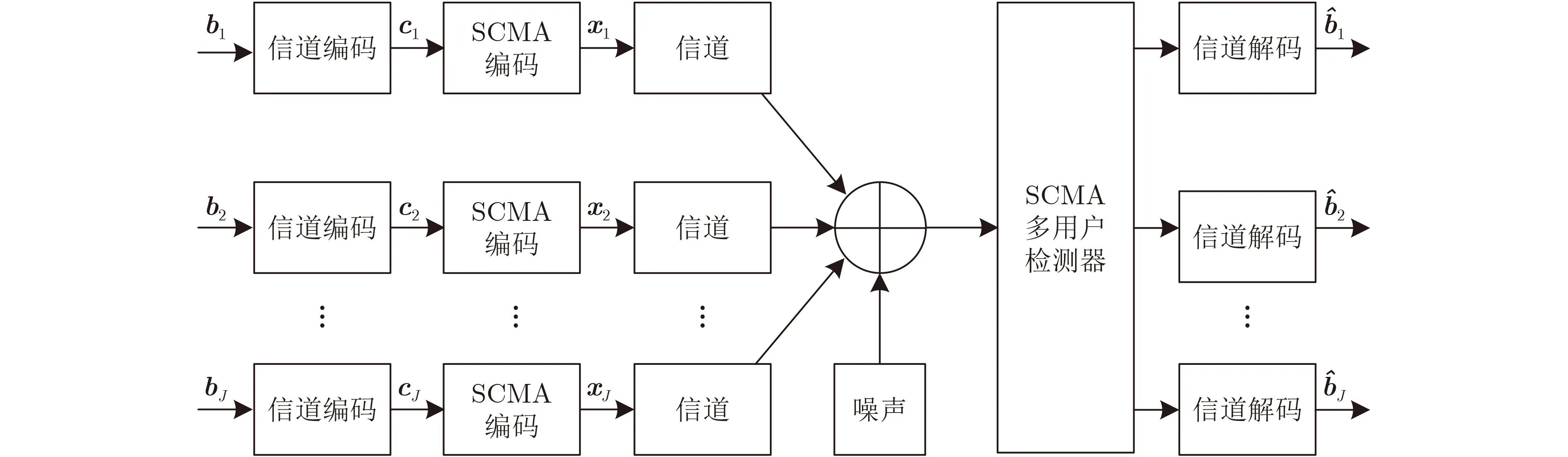
图1 SCMA上行链路模型

图2 SCMA编码过程
其中,行代表资源,列代表用户。以式(1)为例,令dr=3为行重因子,表示每个资源占据的用户数,dv=2为列重因子,表示每个用户占据的资源数。由此可知每个资源同时被3个用户共享,每个用户占据2个资源,这样就限制了每个资源上叠加的用户数目,也保证了用户的信息不会在所有资源上分布,从而减小了用户之间的干扰。
在接收端,接收信号是所有用户信号的叠加[7]

其中,y=[y1,y2,...,yK]T为用户的接收信号,hj=[h1j,h2j,...,hKj]T为第j个 用户的信道增益,xj=[x1j,x2j,...,xKj]T为第j个用户的码字,n~CN(0,N0I)为高斯噪声矢量。
2.2 MPA算法
由于各用户码字的稀疏性,接收端可以采用MPA算法来进行多用户检测,消息传递过程可用如图3所示的因子图来描述,因子图中的两类节点分为用户节点和资源节点,消息沿着用户和资源节点之间的边缘传递[23]。MPA算法步骤如下[23,24]:
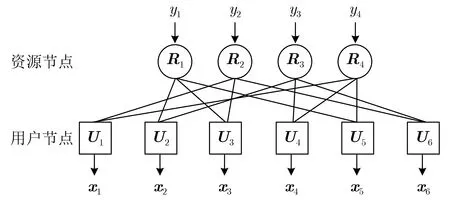
图3 SCMA因子图
将系统中第k个资源上发送的符号记为xk,j,第k个资源上的接收信号记为yk。令表示在第t次迭代中第k个资源节点传递给第j个用户节点的消息值;表示在第t次迭代中第j个用户节点传递给第k个资源节点的消息值。
步骤1 资源节点更新。在第t次迭代过程中,资源节点k传递给用户节点j的消息为
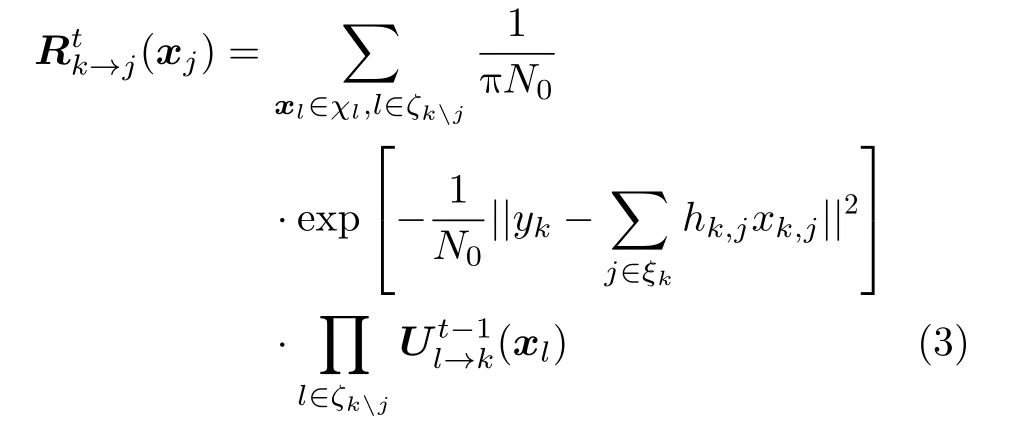
其中,χl为第l个 用户的码本空间,|χl|=M,ξk表示与资源节点k相连的用户节点集合,ξkj表示除用户节点j外与资源节点k相连的其他用户节点集合。
步骤2 用户节点更新。在第t次迭代过程中,用户节点j传递给资源节点的消息为

其中,ξjk表示除资源节点k外与用户节点j相连的其他资源节点集合,p(xj)为给定码字xj的先验概率。
步骤3 后验概率更新。当达到预定迭代次数T后结束迭代,并将与用户节点相连的所有资源节点消息传递给用户节点,作为该用户发送符号的后验概率
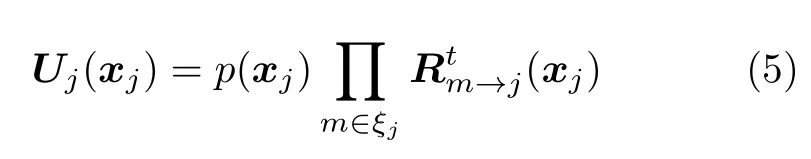
其中,ξj表 示与用户节点j相连的资源节点集合。
由MPA算法公式可知,算法复杂度主要与码本大小M、迭代次数T、同一资源上接入的用户数即行重因子dr相关。
3 低复杂度检测算法
本节将从码本大小M、迭代次数T、行重因子dr以 及每次迭代参与点数Mdr来归类综述SCMA低复杂度多用户检测算法,然后简要介绍其他形式的低复杂度检测算法。
3.1 5类算法
3.1.1 基于降低码本大小 M的研究
MPA算法资源节点更新的复杂度空间为O(Mdr)。随着码本M增大,复杂度会显著增加,针对这一问题,文献[25]提出了一种扩展的对数域Max-Log(Extended Max-Log,EML)算法,该算法考虑到在迭代过程中使用M维消息可能会导致冗余,由此对消息进行截断即固定选择网格每一列(用户)较大的mc(mc <M)个符号值参与消息迭代。该算法在误码性能和复杂度上获得了一个较好的平衡,但任何信道下的用户mc值都一样,为了自适应于信道状态,文献[25]在EML算法基础上进一步提出了一种信道自适应EML算法(Channel-ADaptive EML,CAD-EML),该算法将网格中每一列符号均值作为阈值,选取大于阈值的mc个符号点参与消息迭代,使得不同信道下的用户mc值不同,从而进一步降低了复杂度,但也因此带来了较大的误码性能损失。针对此问题,文献[26]提出了一种基于动态网格的消息传递算法(Dynamic Trellis based MPA,DTMPA),该算法在每次迭代中,将每一列符号值先降序排列,然后采用差值作为参考,如果第i个差值大于阈值,则将前i个最大值保留下来,如果差值全部小于阈值,则保留所有符号,其中阈值的选取随信噪比变化而变化。该算法不仅使得不同信道下的用户mc值不同,且使同一信道下的用户在每次迭代中mc的取值也不同,可以获得比EML算法更低的误码率且比CAD-EML算法更低的复杂度。
3.1.2 基于降低迭代次数 T的研究
MPA算法基于并行方式更新消息,即先更新所有资源节点的消息再更新所有用户节点的消息,这种并行方式会导致先更新的消息无法及时得到利用。为解决这一问题,文献[27]提出了一种基于串行更新的消息传递算法(Shuffled MPA,S-MPA),该算法能够在当前迭代中立即传播已更新的消息,从而可以加快收敛速度,减小迭代次数,达到降低复杂度的目的。但该算法采用的是预先定义的顺序进行消息更新,无法保证最可靠的消息及时被应用。基于此,文献[28]提出了一种改进的基于串行调度的消息传递算法(Improved Serial Schedulingbased MPA,ISS-MPA),在该算法中,用户节点的调度顺序根据新获得消息更新的最大数量来确定,然后用户节点按已经确定好的调度顺序来串行更新,从而可以有效地解决S-MPA算法中由于预定义顺序带来的不足。文献[27,28]提出的算法虽然都加速了收敛,但是没有考虑到收敛速度不同带来的影响。针对此问题,文献[29]提出了一种基于避免冗余迭代的低复杂度多用户检测算法(Avoiding Redundant Iterations-MPA,ARI-MPA),该算法在每次迭代结束前计算所有码字的收敛率,如果所有码字的收敛率都小于预设的阈值则认为已经收敛,剩余的迭代就被认为是冗余的,在其余的解码过程中不需要再继续进行。文献[30]提出了一种残差辅助的消息传递算法(Residual-aided MPA,R-aided MPA),该算法考虑随着算法的收敛,迭代前后消息之间的差异(即残差)将趋于0,因此如果因子图中消息有大的残差说明该消息没有收敛,则其将首先被更新,从而在误码性能和复杂度之间获得一个较好的平衡。
3.1.3 基于降低行重因子d r 的研究
针对MPA算法复杂度随每次参与迭代的边缘数即行重因子dr指数增长的问题,学者主要从基于信道系数和基于因子图两方面进行了相关研究。
3.1.3.1 基于信道系数
文献[31]提出了一种基于边缘选择的消息传递算法(Edge Selected MPA,ES-MPA),该算法只选择信道质量较好的部分边缘来更新从资源节点到用户节点的消息,未选中的边缘被视为干扰并利用高斯近似的方法来计算。同时,为了补偿信息损失,更新高斯模型的均值作为反馈,从而可以保证在降低复杂度的同时几乎不损失误码性能。但该算法没有考虑到用户信道之间的差异,在边缘的选择上是固定选取的,即每个资源节点选择的边缘数相同。基于此,文献[32]提出了一种基于阈值的边缘选择消息传递算法(Threshold-Based criterion for the ES-MPA,TB-ES-MPA),该算法基于给定阈值动态地选择大于阈值的边缘参与消息迭代过程,从而可以根据信道增益动态地将部分高斯近似应用于干扰,在保证误码性能与ES-MPA算法等价的同时进一步降低了复杂度。
3.1.3.2 基于因子图
文献[33]从降低每次迭代需要遍历的点数着手,提出了一种基于部分边缘化(Partial Marginalization,PM)的消息传递算法,该算法在迭代次数小于值m时,按原始MPA算法进行消息迭代,在迭代次数大于m后,只有前面J-t个元素参与迭代,从而有效地降低了复杂度,但同时也带来了较大的误码性能损失。考虑到变量节点的置信度,文献[34]提出了一种动态消息传递算法(Dynamic MPA,DMPA),其基本思想为当变量节点近似收敛时,停止更新概率信息,然后在下一次迭代中动态地去除这些在原始因子图中已经收敛的变量节点,从而在误码性能和复杂度上获得了一个较好的平衡。文献[35]提出了一种基于动态因子图的消息传递算法(Dynamic Factor Graph-MPA,DFGMPA),在资源节点更新过程中,该算法通过使因子图中G个较大置信度分支在当前以及接下来的迭代中将不参与消息传递,而在用户节点更新过程中与原始MPA算法一样,从而在保证了误码性能的同时降低了复杂度。文献[36]提出了一种基于高斯近似的消息传递算法(Gaussian Approximationbased MPA,GA-based MPA),该算法通过将因子图上的原始离散消息近似为连续高斯消息,避免了原始MPA算法复杂的边缘化操作,从而使得复杂度随着码本大小呈线性增长。
3.1.4 基于降低每次参与迭代点数M dr的研究
MPA算法每次迭代需要遍历Mdr个叠加星座点(Superpose Constellation Points,SCPs)数,搜索空间较大,为解决这一问题,文献[37]提出了一种基于动态阈值的消息传递算法(Dynamic Thresholdbased MPA,DT based-MPA),该算法核心思想为在不同的信噪比下挑选不同数量SCPs参与资源节点迭代更新过程。当信噪比小时,噪声和信号混合在一起,译码时难以分开,此时选择更多的SCPs参与MPA迭代;当信噪比大时,噪声对信号的影响较小,容易将噪声与信号分开,此时选择更少的SCPs参与MPA迭代过程。从而在保证误码性能的同时降低了复杂度。考虑到在一次迭代过程中,条件信道概率(Conditional Channel Probability,CCP)的计算占总计算的60%,且低CCP状态对最后判决影响较小,由此文献[38]提出了一种动态缩减平方搜索(Dynamic Shrunk Square Searching,DSSS)算法,该算法只在高潜在状态子空间内进行消息传递,从而可以减少复杂的CCP计算。同样考虑到资源节点更新过程搜索空间过大问题,文献[39]提出了一种基于列表球面解码(List Sphere Decoding,LSD)的消息传递算法,该算法只在给定半径的超球面内搜索出候选列表集,然后将此列表集中的点参与资源节点更新的迭代过程,由此降低了复杂度,但该算法的半径不能依据高斯噪声动态变化,带来了较大的误码性能损失。在此基础上,文献[40]提出了一种基于球形译码(Sphere Decoding,SD)的检测算法,该算法的半径可以依据高斯噪声分布的特性来动态选择,从而在复杂度与误码性能之间取得了一个较好的平衡。文献[39,40]中基于球面译码的方案只能应用于具有一定规则星座结构的SCMA系统,文献[41]表明具有非恒定模量的不规则星座的性能优于其他星座,由此文献[42]提出了一种改进的球形译码(Improved SD,ISD)检测算法,该算法对任意规则或不规则的星座都可以实现最佳的最大似然检测。
3.1.5 其他形式的研究
文献[15]提出了一种对数域的消息传递算法(Max-Log-MPA),该算法在资源节点更新过程中,利用Jacobi公式消除了原始MPA算法中大量的指数运算,从而解决了硬件实现过程中由于指数运算造成的数值上下波动大、行效率低的问题。为了弥补文献[15]中的误码性能损失,文献[43]提出了另一种对数域消息传递算法(LOG-MPA),该算法在利用Jacobi公式消除指数运算时,加上了修正项,使得算法在几乎不增加复杂度的同时,改善了误码性能。文献[44]提出了一种权重消息传递算法(Weighted MPA,WMPA),该算法通过引入权重因子使得接收码字与传输码字的距离减小,从而提高了正确译码的概率,该算法由于不需要迭代过程,因此较大地降低了复杂度,但是也因此导致误码性能有所下降。文献[45]提出了一种离散化消息传递算法(Discretized MPA,DMPA),该算法通过离散层用户节点中的概率密度函数,使得资源节点更新消息的时间变为多项式时间而不是原始MPA算法中的指数时间。针对超奈奎斯特采样(Faster-Than Nyquist,FTN)信号和SCMA联合系统,文献[46]基于自回归(Auto Regressive,AR)模型和MPA算法,设计了一种联合信道估计和信号检测的算法,该算法中所有消息都以高斯封闭的形式表示,从而使得算法复杂度随用户数只呈线性增加。此外,针对免调度传输的FTN-SCMA系统,文献[46]进一步提出了一种联合活动用户检测、信道估计和信号检测的算法,该算法利用期望传播(Expectation Propagation,EP)近似值重构特定的因子节点,从而可以使算法保持较低的复杂度。针对具有多个接收天线的上行SCMA系统,文献[47]通过在信道条件好的资源上执行联合高斯算法(Jointly Gaussian Algorithm,JGA),在信道条件差的资源上采用最大似然算法对传输的符号进行恢复,提出了一种基于资源选择的消息传递算法(Resource-Selection Based MPA,RSB-MPA)。文献[48]基于确定性消息传递算法(Deterministic MPA,DMPA),提出了提前终止、自适应、初始噪声减少以及初始概率近似算法,并用所提出的算法改进了级折叠解码器,在满足吞吐量和时延要求的前提下,获得了更低的复杂度和更高的硬件效率。
3.2 各类算法举例
本节将从3.1节介绍的5类算法中,分别举一例详细介绍其算法原理并进行复杂度对比,算法均采用对数域形式。
3.2.1 算法原理
3.2.1.1 LOG-MPA
文献[43]提出的LOG-MPA算法的核心思想为利用Jacobi公式消除指数运算的同时加上修正项以减少误码性能损失,可以用式(6)表示
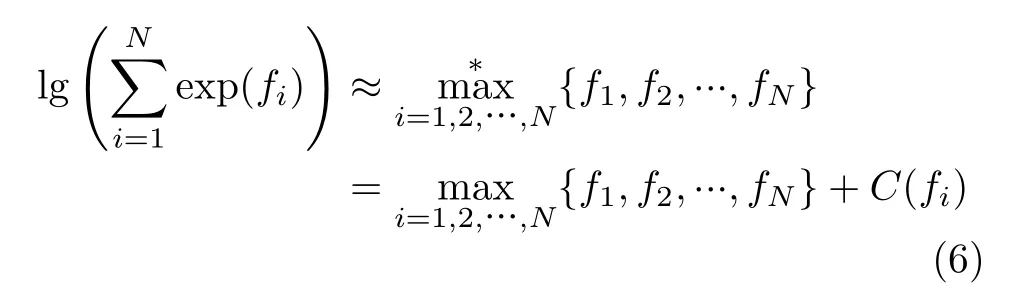
其中,C(fi)为修正项。LOG-MPA算法具体步骤如下:
步骤1 资源节点更新

3.2.1.2 DT-MPA
文献[26]提出的DT-MPA算法基于网格来表示码本大小为M的活动用户消息传递过程,由于采用对数域消息值,所以可以利用差值来表征消息值大小相邻的符号之间的置信度差异。在每次迭代时,如果排序后前后两个网格点的差值大于阈值τ,则认为前面网格点的置信度远大于后面网格点的置信度,此时只选择前面网格点参与后续迭代并除后面网格点。如果差值不大于阈值,则说明前后两个网格点置信度相近,此时需要全部选取。通过仅保留满足阈值条件的网格点,删除不满足阈值条件的网格点,从而将用户的码本大小由M降低为mc[t,ξk(i)],其中mc与迭代次数t以及资源k上的用户i(ξk(i))有关。与LOG-MPA算法迭代过程相比,该算法只是消息更新过程中的码本空间不同,资源节点和用户节点更新过程分别如式(10)和式(11)所示

其中,为第l个 用户第t次迭代时的码本空间。
3.2.1.3 ISS-MPA
文献[28]提出的ISS-MPA算法通过采用串行迭代,使得资源节点更新的消息可以立即用于用户节点更新过程,且用户节点的调度顺序根据用户新获得消息更新的最大数量来选择,只需线下手动计算即可得到。令αk,k=1,2,3,4记录与资源k相连用户的消息更新数,=1,2,...,6记录用户可访问的最新消息更新的总数。每次选择用户传递消息前,先计算各用户的βj值 并选中βj最大的用户βj*,同时将βj*置0。若各用户βj*值相同,则随机选中。下面以2.2节中因子图为例来说明调度顺序的计算方法,详细过程如图4所示。当消息未更新时,αk和βj皆为0,如图4(a)所示。随机选中用户1后,对应的α2和α4变为1,随后β3,β4,β5和β6变为1,如图4(b)所示。选中用户3后对应的α1,α2分别变为1和2,β1变为1,β5和β6变为2,如图4(c)所示。类似地,可推出用户调度顺序为1→3→5→2→4→6。与LOG-MPA算法迭代过程相比,该算法只是资源节点更新过程不同,资源节点更新过程如式(12)所示
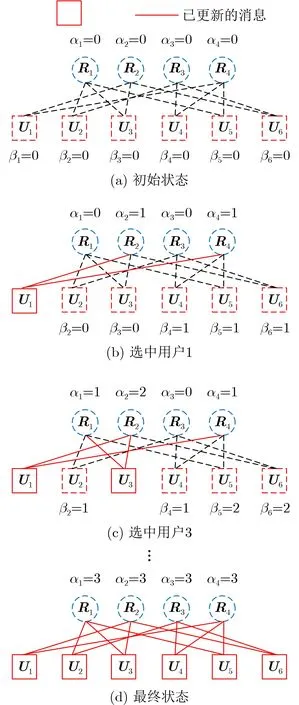
图4 调度顺序计算过程示意图

3.2.1.4 ES-MPA

其中,D[xk,i]为剩余边缘相对应符号的方差。与LOG-MPA算法迭代过程相比,该算法只是资源节点更新过程不同,资源节点更新过程如式(15)所示
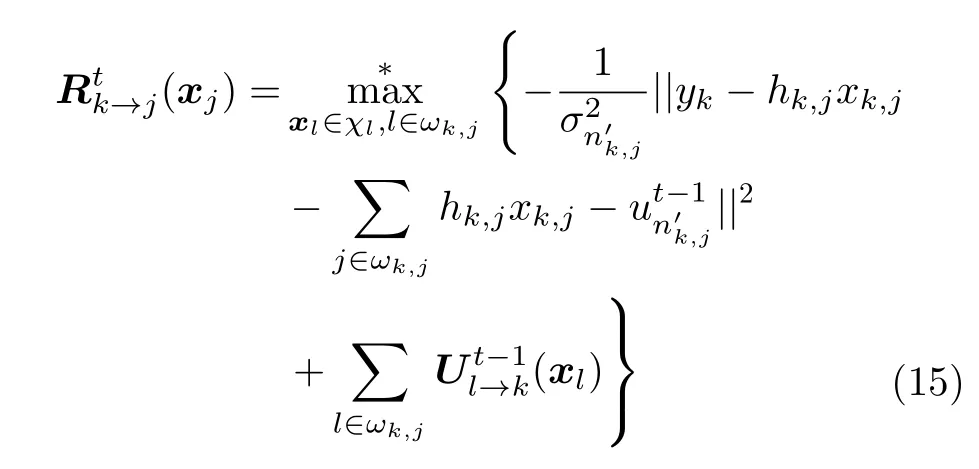
3.2.1.5 SD-MPA
文献[40]提出的SD-MPA算法考虑到与接收信号欧氏距离较近的叠加星座点更可能准确译码,因此在资源节点更新过程中只选择给定圆形半径r范围内的叠加星座点集参与消息迭代,r可以利用高斯噪声的分布特性来决定,从而可以在误码性能和复杂度上获取平衡。与LOG-MPA算法迭代过程相比,该算法只是将搜索空间由O(Mdr)变成了O(φ(k)),φ(k)为资源节点k上给定半径范围内的叠加星座点,资源节点更新公式如式(16)所示

其中,X={x1,x2,...,xJ}表 式与资源节点k相连的各用户的码字。
3.2.1.6 DFG-MPA
文献[35]提出的DFG-MPA算法通过根据上一次迭代的概率分布来计算当前置信度,使G条置信度较大的分支由因子图上的实线变成虚线,在资源节点更新过程中不参与当前以及接下来的迭代,剩余的实线分支则继续参与迭代。在用户节点更新过程中,实线与虚线分支和原始MPA算法一样,都参与消息迭代。因子图将在迭代过程中自适应地不断变化更新,直到达到最大迭代次数或所有分支保持不变时停止更新。与LOG-MPA迭代过程相比,DFG-MPA算法只是资源节点更新过程不同,更新如式(17)所示

3.2.2 复杂度分析
表1和表2分别列出了3.2.1节所述的6种算法的加法和乘法计算复杂度。为便于分析,下面将以ISS-MPA算法为例详细分析其复杂度,其余算法可以类似推导。此处1次指数、对数、平方运算分别视为1次乘法,max{n}和sort{n}分别视为n次加法运算[26]。资源更新过程的复杂度计算分为两步:首先计算式(12)m*ax内部公式所需复杂度,其对应最左边项需要计算dr次 加法、(dr+1)次乘法、1次平方运算,其余项需要计算(dr+1)次加法、0次乘法,考虑到每个资源节点连接dr个用户,每个用户遍历的多维码字星座点数为M,所以搜索空间为Mdr,再考虑到迭代次数为T′,资源节点数为K,所以此部分需要计算T′KdrMdr(2dr+1)次加法和T′KdrMdr(dr+2)次乘法运算;然后按式(6)计算m*ax 本身所需复杂度,此时需要(Mdr-1-1)次max 运算、2Mdr-1次加法运算、Mdr-1次指数运算和1 次对数运算,所以此部分共需计算T′Kdr(3Mdr-M)次加法和T′Kdr(Mdr+M)次乘法运算。用户节点更新过程由于计算的是外信息,所以1次消息传递需要进行 (dv-2)次加法、0次乘法,考虑到有J个用户,每个用户连接dv个资源,所以共需计算T′JdvM(dv-2)次加法和0次乘法运算。后验概率更新时需要将与用户节点相连的所有资源节点消息传递给用户节点,所以需要JM(dv-1)次加法和零次乘法运算。由此可得ISS-MPA算法复杂度如表1和表2所示。

表1 LOG-MPA算法与各类算法加法复杂度对比分析

表2 LOG-MPA算法与各类算法乘法复杂度对比分析
4 仿真结果与分析
本节将对3.2.1节中6种算法进行仿真性能分析。仿真参数如表3所示。在4.1节至4.3节中,LOGMPA,ES-MPA,DT-MPA,SD-MPA以及DFGMPA算法的迭代次数都设置为4次,ISS-MPA算法迭代次数都设置为2次。
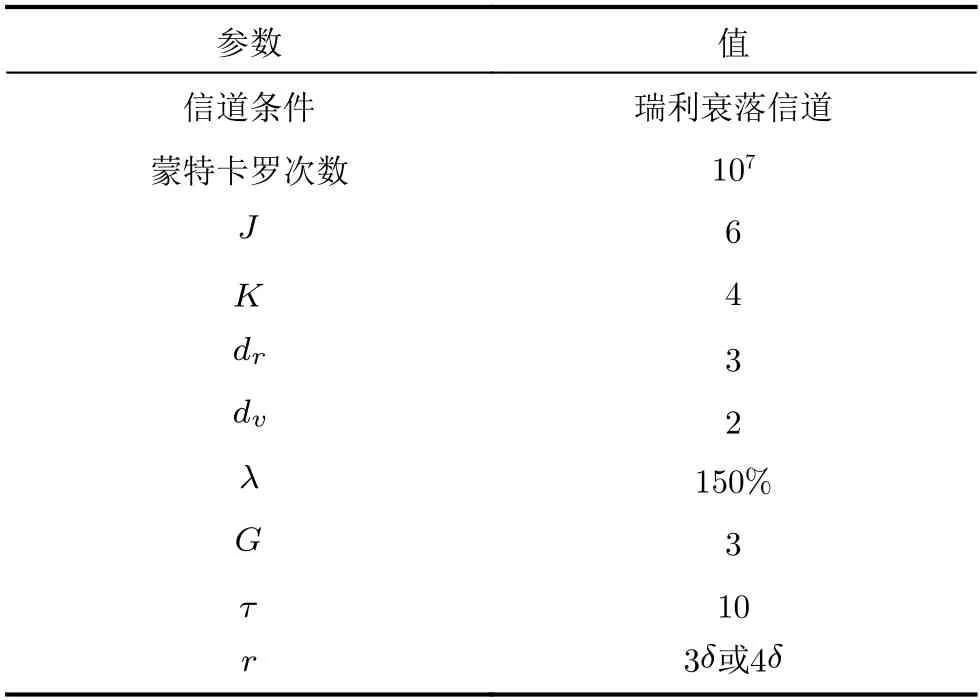
表3 仿真参数
4.1 误码率对比
图5显示了LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法误码率性能对比情况。由图5可知,相比于其他算法,ESMPA算法误码性能最差。半径为4δ的SD-MPA算法误码性能优于半径为3δ的SD-MPA算法。DT-MPA算法和半径为4δ的SD-MPA算法误码曲线与LOG-MPA算法基本重合,在误码率为10–3时,ISS-MPA,DFG-MPA以及半径为3δ的SD-MPA算法与LOG-MPA算法相比,分别损失约0.26 dB,0.37 dB以及0.56 dB。ISS-MPA 算法2次迭代时的误码性能就几乎可以达到LOG-MPA算法4次迭代时的误码性能,这是因为ISS-MPA算法能立即传播已更新的消息,在2次迭代时算法已经收敛。
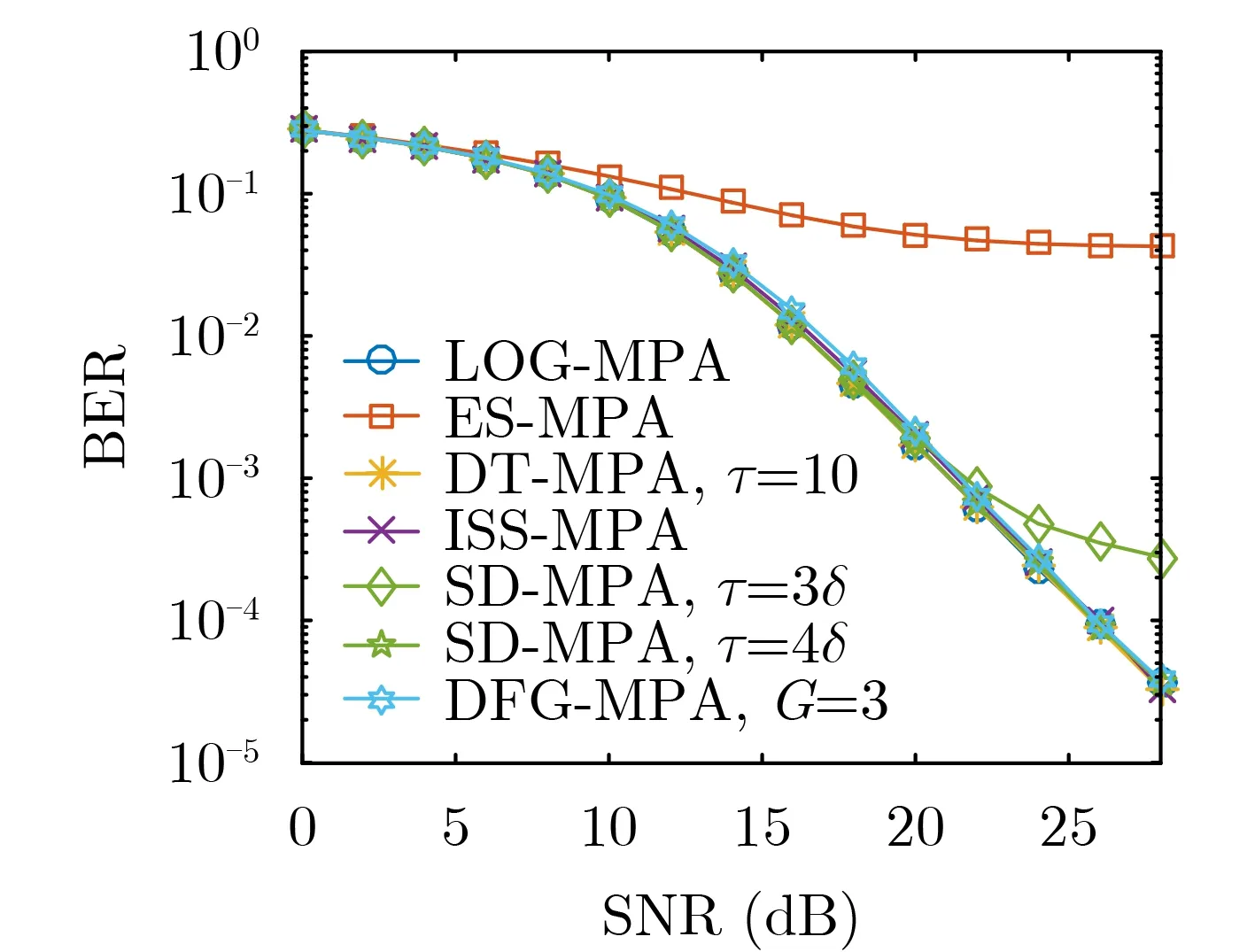
图5 LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法误码性能对比
4.2 复杂度对比
图6显示了LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法的加法和乘法复杂度对比情况。由图6可知,半径为3δ的SD-MPA算法复杂度低于半径为4δ的SD-MPA算法。DT-MPA和SD-MPA算法复杂度都随信噪比增大而减小,信噪比较小时,SD-MPA算法复杂度降低不明显,与其他算法相比,DT-MPA算法乘法复杂度最低;信噪比高于20 dB后,相比于其他算法,半径为3δ的SD-MPA算法加法乘法复杂度都最低,与LOG-MPA算法相比可分别降低91.58%的加法复杂度和90.13%的乘法复杂度。

图6 LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法复杂度对比
4.3 信道估计下的误码性能分析
准确地估计每个用户的信道状态信息对于接收端多用户检测有重要的作用。然而,在实际系统中,信道估计误差是难以避免的。因此,分析信道估计误差对系统误码性能的影响具有实际意义。信道估计误差可以定义为[49]

图7显示了在信噪比为25 dB时,信道估计误差对 LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法误码性能的影响。从图7可以看出,SD-MPA对信道估计误差最敏感,当信道估计误差的方差为0.01时,SD-MPA在半径为3δ和4δ下的误码率分别恶化到了0.142和0.069。ISS-MPA和LOG-MPA的误码性能曲线基本重合,这意味着信道估计误差对两者的影响基本相同,在信道估计误差的方差为0.01时,ISS-MPA和LOGMPA的误码率近似为0.006。随着信道估计误差的增大,ISS-MPA的误码率收敛到0.086,相比于半径为4δ的SD-MPA有0.219的增益。与其他算法相比,ES-MPA的误码性能曲线对信道估计误差的变化幅度最小,这是因为ES-MPA的误码性能在信道估计误差为零时的误码性能就已经相对较差。从整体上来看,信道估计误差对算法的误码性能影响很大,且随着信道估计误差的增大,算法的误码性能急剧下降。在信道估计误差达到一定值后,算法的误码性能开始收敛到不同的误码率,且该误码率均大于信道估计误差为零时的误码率。由此可见,对信道状态信息进行准确的估计对于接收端的多用户检测必不可少。
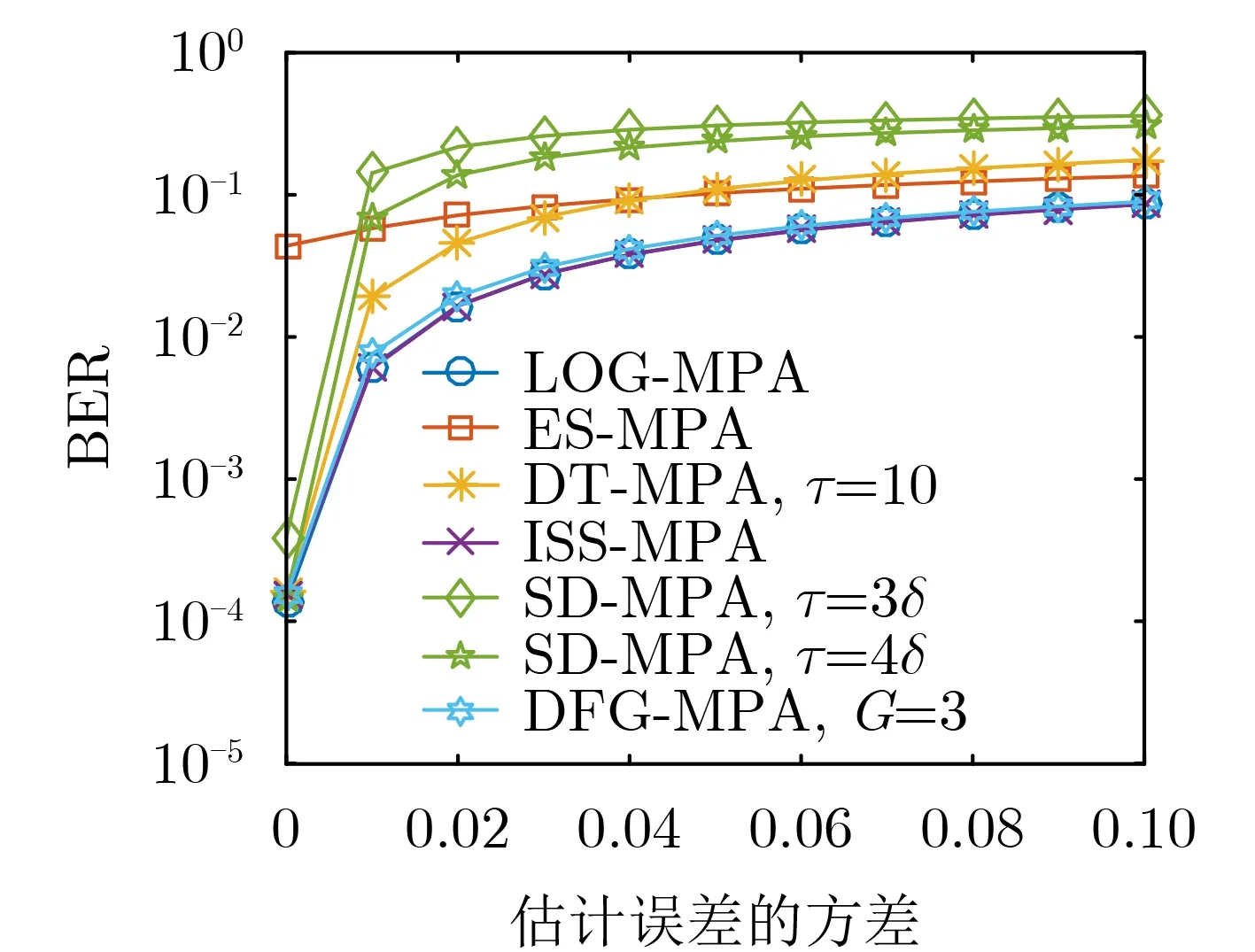
图7 信道估计误差对LOG-MPA,ES-MPA,DT-MPA,ISS-MPA,SD-MPA以及DFG-MPA算法误码性能的影响
对比图5—图7可以发现,在信道状态信息理想情况下即没有信道估计误差时,DT-MPA在误码性能和复杂度上可以获得较好的平衡;在存在信道估计误差时,ISS-MPA受信道估计误差影响相对较小,对误码性能和复杂度可以实现较好的折中。整体而言,SCMA多用户检测算法的改进主要围绕降低码本大小M、迭代次数T以及行重因子dr3个因素进行,并在此基础上对不同因素的联合考虑。不同的算法受信道估计误差的影响不同,且随着信道估计误差的增大误码性能急剧恶化,因此在实际系统中,对信道状态信息进行准确的估计对于接收端的多用户检测至关重要。
5 SCMA检测算法发展趋势
(1)SCMA检测算法与大规模多输入多输出结合[51–56]。大规模多输入多输出(Massive Multiple-Input Multiple-Output,Massive MIMO)技术通过利用大量的天线数量同时服务于很少的终端,能够有效地提高频谱效率和信道容量。在SCMAMassive MIMO系统中,接收端进行多用户检测的复杂度和能源消耗会随着天线数量和用户数量的增多而增大,导致实际系统难以承受。因此如何在保证误码性能的同时降低接收端的复杂度和能源消耗是SCMA-Massive MIMO系统面临的难题,也是SCMA检测算法的研究方向之一。
(2)SCMA检测算法与深度学习结合[57–60]。传统SCMA检测算法复杂较高,且与最大似然算法性能上还存在一定差距。近些年来,随着深度学习的不断发展,人们开始将其应用于各大领域。由于深度学习自主学习能力强且能处理复杂的多维问题,所以可考虑将其与SCMA检测算法结合以进一步降低系统复杂度。但深度学习模型设计复杂,且在与SCMA检测结合的过程中需要考虑学习参数的学长,选择的参数太多会导致训练过程很慢,太少则导致误码率过高等问题,因此还是一个重要的研究课题。
(3)SCMA检测算法与信道译码结合[61–65]。信道编码可以有效地提高通信系统的纠错能力和抗干扰能力。将SCMA与信道编码联合设计,可以在提高通信可靠性的同时增大接入的用户数。但是接收端如何对SCMA多用户检测和信道译码进行联合设计以在保证误码性能的同时,降低接收机的复杂度和时延仍是一个值得关注的问题。
(4)SCMA检测算法与压缩感知技术结合[66–69]。在上行免调度SCMA系统中,接收机进行多用户检测之前需要预先获得用户的活动状态信息。然而,在实际应用场景中由于大规模用户中任何一个都可以随机进入或离开系统,导致用户的先验信息难以获得。压缩感知(Compressed Sensing,CS)是一种稀疏信号恢复理论,可以用于估计资源的占用情况。因此,可以将SCMA检测算法与CS技术结合用于进行活动用户的检测,从而可以在获取用户活动状态的信息的同时降低系统的复杂度。但是SCMA检测算法与CS技术结合后,系统的性能与信道条件密切相关,在平坦衰落信道下,可以准确地检测活动用户,但在频率选择信道下准确性会有所降低。因此SCMA检测算法与CS技术的结合也是值得探究的问题。
(5)SCMA检测算法与索引调制结合[70–74]。索引调制(Index Modulation,IM)通过将待传输的信息比特分为索引比特和调制比特两部分,并根据索引比特激活一部分资源来传输信息,同时其他未被激活的资源在发送端发送信息时保持静默状态,具有高能效、低功耗和低复杂度等优点。由此,将SCMA与IM结合有利于进一步提高未来通信系统的性能。但是IM-SCMA结合后,在接收端检测时,如何将索引符号和调制符号联合检测以在获得接近最大似然检测性能的同时降低算法复杂度,还是一个亟待研究的问题。
(6)SCMA检测算法与多点协同传输结合[75–77]。多点协同传输(Coordinated MultiPoint,CoMP)技术通过将多个不同的传输点协作地为同一用户发送数据,可以在超密集网络中有效地减轻小区间干扰和提高小区边缘用户吞吐量。将SCMA与CoMP结合,可以在提高频谱效率的同时改善小区边缘用户性能以及减少信道状态信息获取的开销。但是在SCMA-CoMP系统中,一个用户可以接收来自多个传输点的信号,不同传输点的信号在SCMA多用户检测时相互干扰,因此在接收端如何对来自多个传输点的信号进行检测还是一个具有挑战性的问题。
(7)SCMA检测算法与正交时频空结合[78,79]。在高速移动的环境下,由于多普勒频移的影响,会使系统性能急剧下降。而正交时频空(Orthogonal Time Frequency Space,OTFS)技术可以有效地解决高速移动下多普勒频移带来的性能损失问题。因此可以考虑将SCMA检测算法与OTFS结合,从而使系统在提高用户接入数量的同时,保证高速移动环境下的用户也能进行可靠通信,但是如何检测出接入用户中采用了高斯近似的用户还亟待研究。
6 结束语
SCMA是未来6G系统中极具竞争力的关键技术之一,多用户检测是其中的重要问题。低复杂度的多用户检测算法有利于促进SCMA的实际应用,近些年来吸引了大量研究者的关注。本文从影响算法复杂度的不同因素入手,系统分析了SCMA多用户检测算法的研究现状,并对几种典型算法进行了原理介绍、复杂度分析和仿真性能对比分析。从整体上来看,算法的改进主要围绕降低码本大小、迭代次数、行重因子以及对这些因素的联合考虑来进行。此外,算法的误码性能随信道估计误差的增大急剧恶化,因此对信道状态信息的准确估计对于接收端的多用户检测至关重要,在信道状态信息理想时,DT-MPA算法在误码性能和复杂度上可以实现较好的平衡,在存在信道估计误差时,ISS-MPA算法对于误码性能和复杂度的折中效果更好。最后,本文总结并探讨了SCMA检测算法的发展趋势及面临的挑战。希望能对从事SCMA研究的相关人员提供些许帮助。

