雷达大擦地角海杂波特性与目标检测研究综述

刘宁波 姜星宇* 丁 昊② 关 键

①(海军航空大学信息融合研究所 烟台 264001)

②(军事科学院国防科技创新研究院 北京 100071)

1 引言

对海雷达快速可靠地发现海上目标具有十分重要的意义。对海雷达面临的海面环境复杂多变，存在噪声、干扰、海杂波等诸多因素的影响，其中，海杂波由于功率水平较高，且非高斯、非平稳特性显著，再加之其影响因素的复杂性和多变性，成为影响雷达目标探测性能的主要制约因素之一[1]。当前，海杂波背景下目标检测技术研究以低擦地角为主，大擦地角条件下的相关研究较少。但在天基与高空探测平台、海上作战飞机、弹道式反舰导弹、飞航式超音速反舰导弹以及反舰导弹的末端跃起攻击都涉及大擦地角强海杂波背景下目标探测问题。同时，现有研究表明，随着擦地角的增大，由于杂波分辨单元的雷达散射截面积(RCS)变大，平均后向散射呈单调增加趋势，但幅度统计分布仍然呈现明显的非高斯特点，且海杂波多普勒谱也具有较大差异，表明非连续性尖峰的存在以及Bragg散射分量占主要地位。综合来看，随着擦地角的增大，探测目标的难度也会增大。为此，从雷达目标探测的需求出发，开展大擦地角下的海杂波特性认知研究，掌握变化趋势并建立海杂波模型，是有效改进和创新海杂波抑制算法和目标检测算法、削弱海杂波不利影响、实现探测性能提升的条件和措施[2]。

目前，国内外围绕大擦地角下海杂波特性已开展的研究可归结为两个层面的研究工作[3—5]。一是物理机理层的研究，即在一定的雷达工作参数和外界环境参数条件下(如波段、极化、海况、擦地角等)，利用电磁散射理论，计算海面后向散射系数，并对其起伏情况进行建模与分析；二是试验数据层的研究，即开展基于实际海面或造浪池的海杂波测量试验，利用海杂波试验数据分析海杂波特性及其随雷达工作参数、海洋环境参数等多种因素的变化趋势，并在部分考虑机理或不考虑机理的情况下建立海杂波模型。这两部分研究相互补充，无法相互替代。前者通常具有很高的指导意义，但由于海表面组成成分复杂，且影响因素众多，基于机理建模得到的认知结果通常难以逼真反映实际情况。

本文按照更新时间和技术发展流程的顺序梳理了国内外大擦地角常用数据集、海杂波特性分析、建模及目标检测技术的发展现状。下文按如下形式组织，即第2节梳理总结了雷达大擦地角对海探测数据集，其中重点是常用的Nathanson数据集和Ingara数据集，第3节梳理总结了大擦地角下海杂波的建模研究，包括海表面模型、散射模型和幅度分布模型，第4节梳理总结了大擦地角对海杂波特性的影响研究，第5节梳理总结了大擦地角下雷达对海上目标检测技术研究，最后第6节对全文进行总结与展望。

2 雷达大擦地角对海探测数据集

擦地角指雷达入射波和海平面之间的夹角。通常，大于10°的擦地角被称为大擦地角[2]。

学者们从各种平台和条件下开展了大量大擦地角条件下对海探测试验，并基于此开展了大擦地角海杂波特性研究[6,7]，公开文献资料发表的数据集主要包括：

Nathanson数据集[2,3,8]，总结了从19世纪60～70年代开始针对海杂波进行的一系列测量试验，给出了大约60项试验获取的后向散射数值。该数据集覆盖了0.1°,0.3°,1.0°,30°和60°等不同的擦地角，0～5级海况，包括9.3 GHz的X波段在内的不同雷达频率，给出了HH和VV极化下的后向散射系数σ0。该数据集中的后向散射系数基本上均来自试验数据，但对数据当中明显有错误之处进行了内插和外推处理。该数据集中并没有给出σ0随方位角(相对于风向)变化而出现的变化，而是计算了所有方位角条件下的平均后向散射值。

美国海军研究实验室(NRL)4FR数据集[2,3,9]是在20世纪60年代后期Guinard和Daley使用4FR(UHF、L、C和X波段)系统在5°～90°擦地角、顺风/逆风/侧风、2.57～25.7 m/s风速、水平发射-水平接收(HH)/垂直发射-垂直接收(VV)极化条件下测量了海面后向散射回波，获取了海面后向散射系数。试验中，雷达系统用标准金属球进行校准，用测量船只记录了观测海域的风速、浪高等信息。4FR试验首次在如此宽的雷达频率范围内采集了机载雷达海杂波数据，在海杂波研究历程中具有十分重要的意义。利用该数据，研究人员系统梳理了海杂波与擦地角、频率、极化和风速/风向等因素的依赖关系，并与Masuko等机载测量结果进行了对比分析。

Masuko数据集[2,3,8]是1986年Masuko等人公开的1980年和1981年在日本外海两个试验地点获取的大擦地角海杂波测量数据集。该数据集主要获取了X和Ka波段雷达在HH和VV极化下后向散射系数σ0的测量结果。为了在全方位角(0°～360°)下对各所选的擦地角进行测量并获得具有统计意义的样本，该项试验沿预订航行路线重复飞行了多次，每次飞行都保持在3100 m高度，所选擦地角为20°～90°，步进10°，数据处理时对多次测量的后向散射进行了平均处理，标准差在0.3～1.0 dB之间。对于数据收集时间的海面参数测量，在第一试验地点使用了气象水文浮标自动测量，在第二试验地点则利用船只进行了手工测量。该试验覆盖的风速条件为3.2 m/s,7.9 m/s,9.3 m/s和14.5 m/s，数据均为多次测量的平均值，且假定试验区域内风速均匀。

Ingara数据集[2,3,9]是澳大利亚国防科学与技术组织(DSTO)利用全极化X波段雷达系统Ingara[2,3,9]开展试验获取的数据。该数据集涉及两个不同区域、两种不同条件下的试验，第1次海杂波测量试验编号为2004(SCT04)，试验海域为南澳州林肯港南大约100 km处的南部海域[10,11]。由于所选试验海域位于南澳州大陆架边缘，因此，几乎不存在浅水区对浪场的影响。试验期间，研究人员分8天在不同海况条件下收集了一系列几何形状目标的海面后向散射数据。第2次海杂波测量试验编号为2006(MAST06)，试验海域为北领地靠近达尔文市的沿海和外海海域，研究人员也获取了一系列几何形状目标在不同海况条件下的数据。本次试验共收集了4天的数据，其中2天在距达尔文市25 km左右的沿海地区，2天在达尔文市以西约200 km的外海区域。在收集海面后向散射数据期间，Ingara按照环扫聚束模式运行，即飞行器按逆时针方向绕指定兴趣点(观察海域)飞行，而雷达束波则一直指向兴趣点。在雷达沿360°航行路线飞行过程中连续不断地收集回波数据，并适时调整雷达发射脉冲重复频率(PRF)，保证不同的发射脉冲位置之间具有固定的空间间隔。在该模式下，一次数据收集称之为一次“运行”，单次“运行”数据收集过程可能飞机沿航线飞行多次。为分析擦地角对海面后向散射的影响，试验中选取了不同海拔高度和圆形航线半径。SCT04和MAST06数据均是在预定擦地角15°至45°，增幅为5°条件下收集的兴趣点数据。目前，很多公开文献均采用了Ingara数据集研究大擦地角下海杂波特性和目标检测技术。

3 海表面散射模型与大擦地角海杂波模型

3.1 海表面散射模型

常见海表面散射模型包括Bragg共振散射模型、复合表面模型、海尖峰模型等。

Bragg共振散射模型在Rice[12—14]提出电磁散射的摄动理论后，由Peake[15]应用在雷达散射截面积、Wright[16,17]推广到水面得到。研究发现，雷达后向散射可以通过风和浪分量进行阐释。在风域和风速极小时，由1阶共振可以看出，雷达后向散射与水浪幅度的平方成正比。可以用来解释小幅度、机械产生的水浪数据。

如图1Bragg共振示意图[2]。粗曲线表示海平面频谱的共振分量，细射线表示入射雷达电磁波。当雷达电磁波传播至相继海浪波峰的路程差为雷达波长λ的一半时，即会出现1阶共振。这种情况下，相继反射同相叠加，通过强化或共振的方式产生强后向散射。同样可以看出，当雷达波传播至相继海浪波峰的路程差为λ/2的任意整数倍时，也会产生相同结果。设θ为擦地角，共振海浪的波长为Λ，那么Bragg共振的条件为

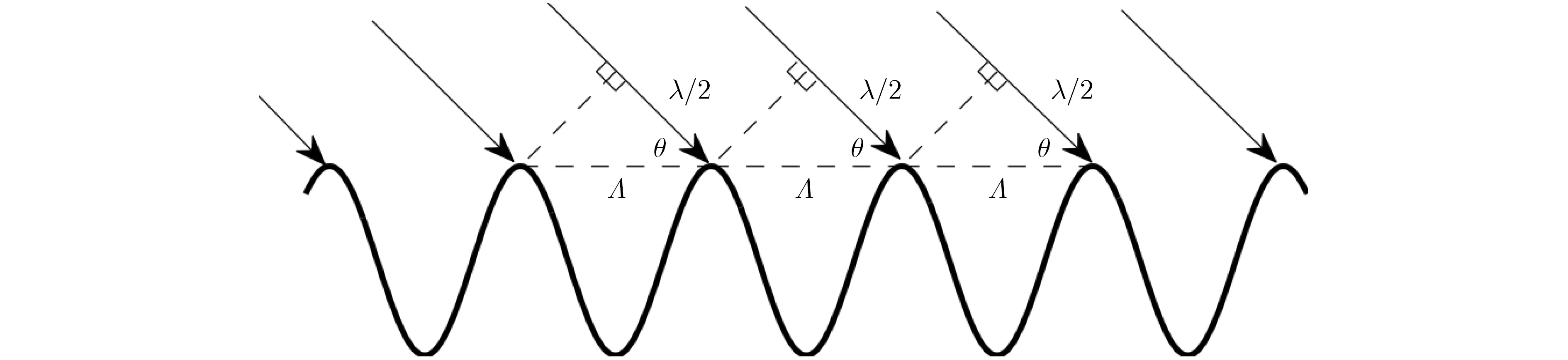
图1 雷达波长和海浪波长的一阶Bragg共振示意图，散射的波同相叠加增强

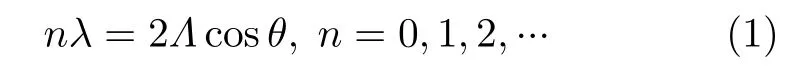
但该模型并没有涉及流体动力学调制等非线性因素影响，同时无法拟合海平面的破碎波/波峰碎白浪花、泡沫和喷溅等非Bragg散射物理结构。

针对上述问题，研究人员对1阶Bragg散射理论进行了拓展，提出了双尺度复合表面模型[12,17—20]。将粗糙表面分为大尺度和小尺度分量，大尺度分量进行几何或物理光学处理，小尺度分量则使用现有的摄动理论处理。很多学者都对该理论的变种进行了研究。例如，Valenzuela和Laing[21]使用了各种流体动力学模型来解释双尺度复合模型。

非Bragg散射常被表示为单一分量，称为“海尖峰”。海尖峰通常被定义为有较大多普勒分量的雷达回波，其频宽较宽，后向散射功率较大，HH极化下的回波能量等于或大于VV极化。Lee等人[22]总结了3种有可能导致非Bragg散射的原因，即存在一个即将破碎的海浪，其波长远大于Bragg谐振波；存在一个长波长和大镜面反射的破碎波；由于布鲁斯特角衰减，VV极化信道能量减弱，同时HH极化信道受到多径散射和波谷被大波峰遮蔽的影响。

3.2 大擦地角海杂波模型

小擦地角海杂波特性的分析结论和模型不能直接用于大擦地角在机理方面的考虑在于：低擦地角下海杂波多受遮蔽效应、多径散射等现象的影响，而在大擦地角条件下，海杂波受遮蔽效应和多径散射影响减弱，取而代之的是Bragg散射导致的杂波能量变强，占据主导地位。面对机理不同，有必要对其大擦地角下的海杂波建模进行专门的研究。已有模型主要包括后向散射系数、幅度分布和多普勒谱3个方面[23]。

3.2.1 大擦地角海杂波平均后向散射系数模型

平均后向散射即为归一化的雷达散射截面积，其定义为被雷达电磁波照射的单位面积海平面的散射截面积，常作为雷达接收的后向散射(反射)能力的度量。在擦地角10°～50°区间内，HH极化的后向散射均值通常要比VV极化的均值低，称为“稳定”散射区域。同时，垂直发射-水平接收(VH)或水平发射-垂直接收(HV)的后向散射均值均显著低于VV或HH[7]，其主要原因是水平极化退化为垂直极化才能被垂直极化接收。后向散射均值低，说明退极化现象是存在的，但是能量占比较低。

大擦地角下平均后向散射模型多为在低擦地角平均后向散射模型基础上的摸索和发展得来。目前有很多研究使用了擦地角大于10°的平均后向散射模型，这些模型主要是基于Nathanson数据集得到的。

常用的大擦地角下平均后向散射模型包括：

(1)北约的AAW系统模型，该模型基于已公开发表的实测数据经验拟合[24]，包括1个参考项和4个针对擦地角、海况等级、极化方式和方位角的调节参数。该模型涉及的最大擦地角为30°，且实际应用表明该模型中并未明确考虑大气波导效应影响。

(2)Ulaby模型[25]，给出了一种30°以上擦地角条件下平均后向散射系数建模的方法，针对逆风向、顺风向、侧风向3种情况分别进行经验建模，所建立的模型具有统一的公示表达，即σ0(θ)dB=G(θ)+H(θ)lgU，其中，σ0(θ)dB表示不同风向(逆/顺/侧风向)、不同擦地角θ下的平均后向散射系数，以dB表示；U为风速，单位为m/s；G(θ),H(θ)则为与极化方式、擦地角和风向有关的量，不同相对风向条件下G(θ)与H(θ)取值的差异，则决定了针对不同风向形成不同的经验关系模型。该模型对于稳定散射区域具有较高的建模精度。

(3)科技服务组织(TSC)模型[26]，认为大擦地角下准镜面反射机制起主导作用，小擦地角下漫散射机制起主导作用，总的后向散射为这两个分量的合成，这使得该模型适用于0°～90°擦地角的情况。有研究对该模型进行了改进[27,28]，用于修正顺风方向所预测的最小值与实际观测不相符的情况，同时使得模型所预测的侧风方向最小值与测量值一致。

(4)NRL模型[27]，进一步对Nathanson数据进行拟合优化，最大程度地减小了模型预测结果和试验实测结果之间的偏差，可应用于雷达频率为0.5～35 GHz、擦地角为0.1°～60°场景下后向散射系数预测。

此外，常见模型还包括Masuko[29]模型，考虑了后向散射随5个不同的变量，包括雷达频率、极化、风速、擦地角和方位角的变化关系；Ingara IRSG[30]模型，沿用了Ulaby模型[25]中风速、方位角和擦地角的关系式，并进一步对0°～360°方位角、20°～45°擦地角下的大量数据进行了拟合优化，将所有参数都纳入了一个模型。

3.2.2 大擦地角下海杂波幅度分布模型

大擦地角海杂波幅度分布模型研究多为在低擦地角幅度分布模型基础上的修正，是一个渐进发展的过程，它经历了正态分布、瑞利分布、对数正态分布、威布尔分布、K分布、混合高斯分布等分布模型。

针对大擦地角海杂波，采用的幅度分布模型主要包括：

(1)K分布模型[3]，K分布在大多条件下均能较好的拟合实际测量的海杂波数据。低擦地角状态下，虽然韦布尔分布和对数正态分布可以较好地描述高分辨率雷达下的海杂波幅度分布，但二者均未考虑时空相关性，因此只适合做单点统计。为了描述复杂海况下的大擦地角海杂波，适用范围更广的K分布被采用。作为一种非高斯混合模型，K分布不仅能更优地拟合重拖尾现象，还能从物理形成机理上分析海杂波的组成[1]。2019年，PAN通过实测数据分析证明，广义K分布可以很好地拟合35°擦地角下不同扫描角度下的海杂波[23]；

(2)KK-分布模型，在K分布基础上发展得到，改善了K分布在水平极化与低擦地角下的概率分布建模不准确问题，使用两个K分布来建模Bragg分量和海尖峰，总的杂波分布为两个分量的线性合成。尽管第2参数的选择是任意的，没有直接的物理基础，但该种分布在尾部区域有着精确的拟合[13]。

(3)K+R分布模型[4]，为了捕获数据中额外的瑞利分量，在K分布的基础上增加了一个瑞利分布(参数)，以获得更高的建模精度。实测数据验证表明，这种分布模型适合在相对较少的样本条件下对大擦地角海杂波进行建模[31]。随后，KR分布模型[32]被提出，解决了K+R分布模型参数估计需要计算前3阶矩、计算量较大且无闭合表达式等使用困难的问题。

3.2.3 大擦地角海杂波多普勒谱模型

目前大擦地角下海杂波多普勒谱特性的建模方面，并没有形成统一的观点。低擦地角下比较有代表性的模型分别由Lee和Walker提出。Lee认为多普勒谱由两部分组成[24,26]，分别表示了慢散射体分量和快散射体分量。其中，慢散射体分量即为Bragg散射，与小尺度的张力波有关，可以采用高斯谱建模；快散射体分量多来自于不断演变的碎浪，由杂乱无章的水、泡沫和气泡组成，可建模为Lorentzian谱。该模型在描述多普勒谱时形式比较复杂，但具有一定的准确性。Walker提出的为具有3种分量的高斯型多普勒谱模型，3种分量分别代表了Bragg散射、白浪散射和海尖峰散射，它们共同组成了多普勒频谱模型[29]，形式简单，但是并没有对非Bragg散射作出预测。但近年在对Ingara海杂波进行表征以区分不同类型的散射的研究中发现Walker模型不适用于大擦地角。

为处理大擦地角下的海杂波多普勒谱建模，Luke提出了一种新的两分量模型，该模型同时适合慢速Bragg散射和快速非Bragg散射或海尖峰散射，考虑了20°以上擦地角时布鲁斯特角的减小。使用实测数据对模型进行测试的过程中，估计模型的幅度参数表明，(1)慢速VV通道比HH通道大5～10 dB，快速HH通道返回值始终大于VV通道，表明在HH通道中存在主要快速分量，它导致了高的回波功率，相比于慢速分量而言具有更宽的谱。(2)在两个通道中都观察到正弦变化，在迎风和逆风方向上具有最大值，在侧风方向上具有最小值。(3)慢幅度分量和快幅度分量模型匹配程度随方位角成正弦变化，随擦地角的增加而增加。(4)多普勒谱中心频率随着擦地角的增大呈缩小趋势，对于快速分量更明显。(5)就谱宽而言，慢速分量没有明显的趋势，而快度分量随擦地角的增加有微弱趋势的减小。

Watts[33—35]提出了适合多极化、多视向和中等擦地角下收集的雷达海杂波数据的多普勒谱模型，并用Ingara数据集进行测试。分析中发现，多普勒频率标准偏差的功率谱宽度在范围和时间上以无关于局部谱强度的方式波动。局部谱的平均多普勒频移与局部谱强度具有明显的相关性，在仰风或顺风时尤为明显。在某些情况下，当局部杂波强度超过某个阈值时，谱会进一步展宽，产生明显的双峰谱。

4 大擦地角对海杂波特性的影响

4.1 对雷达后向散射特性的影响

理论分析和实测数据验证均表明，随着雷达擦地角的增大，雷达后向散射增强。相较低擦地角情况，大擦地角下的雷达后向散射呈现明显增强，且变化可以划分为3个明显的区域：近切向入射区、平直区和近垂直入射区。这3个区域的分界点由雷达波长、极化方式和海面起伏状况决定[36]。

图2为后向散射系数随擦地角的经验变化曲线。可以看出，在不同海况条件下都有在近切向入射区内，后向散射系数随着擦地角的增大而迅速增大；在平直区内，后向散射系数随着擦地角的增大而较缓慢地增大。同时，HH极化的后向散射要比VV极化的后向散射受雷达波长的影响更大。在上述两个区内，后向散射系数都随海面粗糙度的增大而增大。在近垂直入射区内，后向散射系数随着擦地角的增大而增加更为迅速，但随海面粗糙度的增大反而趋于减小。3个区域内，都有后向散射系数随着雷达波长的减小而增大。随着海况的增大，相同擦地角下的后向散射系数增大，造成总体变化曲线左移，3个区域的分界值变小。

图2 后向散射系数随擦地角变化曲线

此外，相比于同极化(HH与VV极化)，交叉极化(HV与VH极化)下的后向散射系数随擦地角增大而增加的速度要慢；海面的粗糙程度对后向散射系数的变化率也有影响，海面越光滑(海况等级越低)，后向散射系数随擦地角增加而增大的速度越快[37]。由上可知，随擦地角逐步增大至接近90°，海面后向散射回波的能量将快速提高到很高的水平，此时雷达海上目标检测面临严重的强海杂波背景，检测难度大。

4.2 对幅度分布特性的影响

在大擦地角条件下，后向散射主要归因于粗糙平面的Bragg散射，而白沫散射则是较为次要的分量。

Dong和Haywood[38]研究发现，在海杂波随方位角变化的同时，高阶幅度统计特性基本上不受方位角影响。他们对20°和40°擦地角下的数据进行了分析，并采用K分布拟合，比较两种擦地角下的视向函数(方位角函数，即在不同方位角下的拟合误差函数)发现，相对于VV极化，HH极化数据拟合较好，在低擦地角条件下这一结论也同样明显。

Dong通过K分布对大擦地角海杂波数据的拟合结果，还发现K分布对HH极化海杂波数据的尾部拟合效果不佳，这可能是由于存在离散海尖峰的原因，相对而言，K分布对VV极化海杂波数据具有较好的拟合效果。为了更好地拟合HH极化数据，Dong尝试使用了KA分布进行建模，发现KA分布具备更好的拟合精度，但KA分布参数估计的计算量过大。此外，Dong,Rosenberg等人[13,39]还研究了KK分布对DSTO Ingara数据的建模情况，发现K分布对VV极化数据的建模效果好，KK分布则对HH极化数据建模效果好(如图3所示)，并且还发现对于HV交叉极化数据，KK分布建模效果也稍优于K分布。

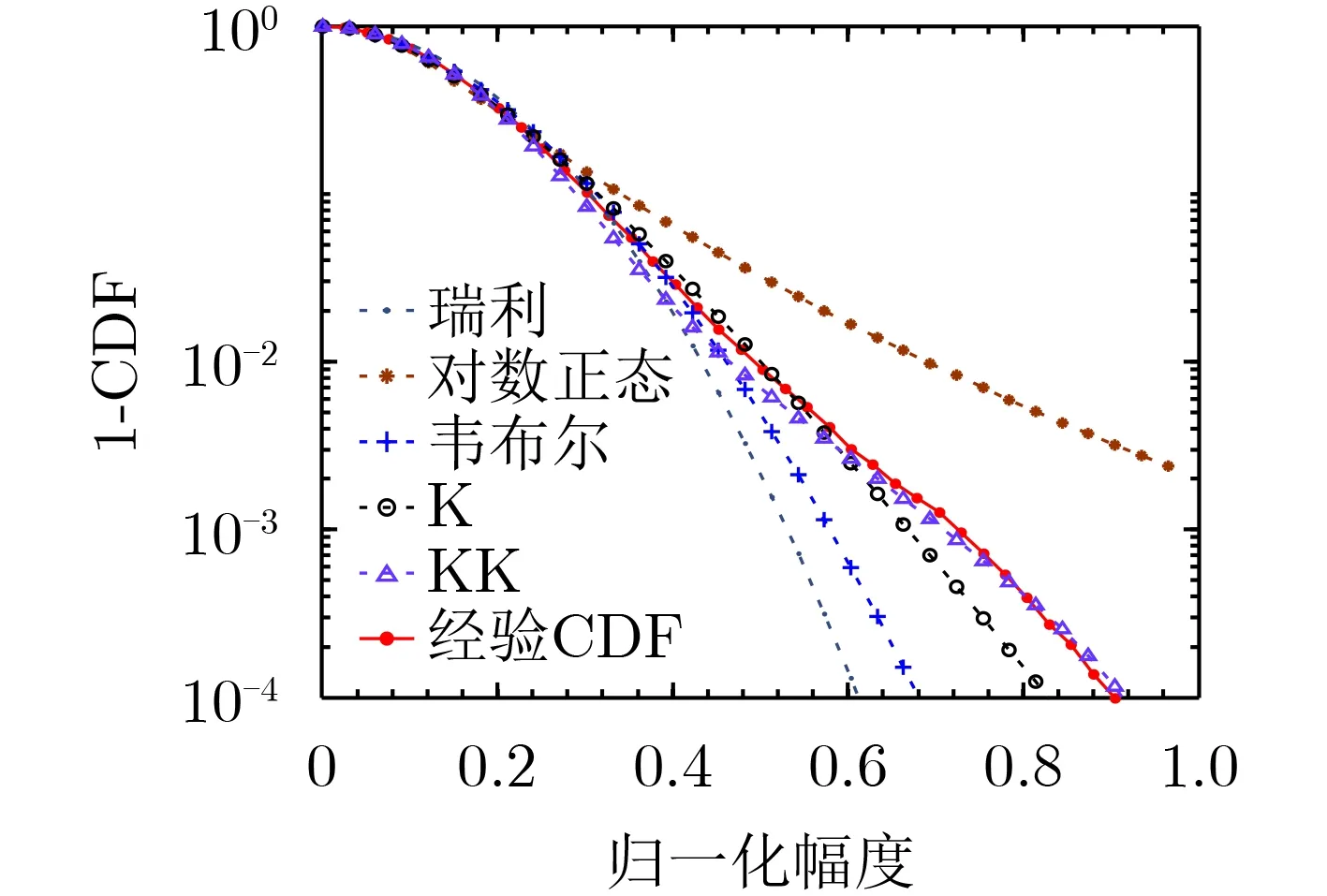
图3 HH极化条件下不同分布模型拟合效果

Crisp等人[40]和Rosenberg等人[41]对大擦地角海杂波数据进行了深入分析，相关结论总结如下：(1)对于HH和VV极化数据，方位角函数随擦地角的增加而增加；(2)方位角函数与方位角之间大体呈正弦式变化，该变化与风向相关，在逆风和顺风向出现峰值。

此外，需特别指出的是，在高分辨率、低擦地角条件下，海杂波幅度分布易出现重拖尾现象，而这一现象与海尖峰频发密切相关，这种重拖尾现象在大擦地角条件下也会出现[1]。

4.3 对相关性的影响

试验表明，大擦地角海杂波相关时间维持在毫秒量级，且随着擦地角增加，先增加后减小，时间相关性最强的擦地角在60°左右，而空间相关性方面，随着擦地角增加，平均相关距离单元个数一直增加[32]。

Dong[42]研究了Ingara数据集中方位(时间)和距离(空间)之间的相关性，发现距离和方位之间的短期相关性均比已有文献报道的时间短，分析原因可能是试验数据对应的大/小擦地角，以及飞行/固定雷达平台差异造成的。而有关长期相关性的分析表明，风浪和涌浪的波长或可从距离相关性中求得，而风浪和涌浪的周期或可从方位相关性中求得。

Dong通过这项研究中还发现，HH和VV极化数据之间的相关性较弱，水平和垂直极化天线同时测量到大幅度回波的概率要比单极化天线测量到的概率明显低。他利用这一特征设计了一种恒虚警(CFAR)检测方案，该方案认为，只有HH和VV极化下某一距离单元的回波分别大于相应的HH和VV极化下的阈值时，才判定该距离单元内存在目标，该方法可以实现虚警的有效控制。

4.4 对多普勒谱特性的影响

在大擦地角条件下对海杂波多普勒谱进行特征描述的公开报道较少，而对其进行建模的文献报道则更少。在第3节介绍的试验数据测量过程中，研究人员对大擦地角区域多普勒谱做了一些分析总结。

Lee等[22]的研究使用了安装于船艏的一台X波段相干散射仪测量得到的10°～70°擦地角区间的海杂波数据，谱特性分析得到如下结论：(1)在逆风向，平均多普勒速度大致以c osθ的比例随擦地角的增加而减小；(2)相比VV极化，HH极化下所观测到的较高速度(多普勒)峰值有所降低，擦地角越大(典型值为θ＞50°)，两种极化下的速度则趋于相等，且频谱形状具有较高的相似度；(3)在逆风向，随着擦地角的减小，HH极化的多普勒峰值与VV极化的多普勒峰值分离，偏向更高的多普勒频率；(4)HH和VV极化下，海杂波的去相关时间均随擦地角增大而增大。

Valenzuela和Laing[21]利用海军研究实验室4频率雷达在10°～30°擦地角下获得的海杂波数据进行了多普勒谱分析。研究人员主要研究了多普勒谱宽度，得到如下结论：(1)对于垂直极化，多普勒谱宽度与擦地角几乎无关，且随着擦地角增加，水平极化下的多普勒谱宽将逐步降至与垂直极化相当的水平；(2)多普勒谱宽度随雷达频率、浪高的增加而增加；(3)多普勒谱宽在逆风向时最大，在顺风向时最小。

此外，Lamont-Smith[43]发现，对于快变散射分量，HH和VV极化下的多普勒谱中心均与擦地角呈线性变化关系，且与风速和雷达频率无关；对于慢变散射分量，多普勒谱中心与擦地角也呈现线性变化关系，但其与风速和雷达频率则呈现复杂相关性。

需要说明的是，在大擦地角(10°以上)条件下，海表面散射机理异于低擦地角条件，具体表现为：布鲁斯特角抑制效应不再显著，削弱了多径的影响，占据主导作用的散射分量为粗糙海面的Bragg散射，以及少量的白浪散射。机理层面的差异导致小擦地角海杂波谱特性分析结论或模型未必适用于大擦地角条件[13]。

5 大擦地角海杂波中目标检测

海上目标检测技术是对海雷达信号处理研究的重要领域，现有研究主要针对小擦地角情况。大擦地角海杂波背景下目标检测面临的主要问题是等效后向散射面积增大，大部分海杂波能量投射到少数距离单元，能量分布不均，出现幅度突然增强的海杂波“异常单元”，导致检测器参考单元所处的背景环境复杂多变难以预测，造成虚警概率增大[44]。尽管专门针对大擦地角的相关研究在不断进展，但目标检测技术的设计相对较简单，主要基于某种分布模型进行相应的目标检测方法设计或深度学习与神经网络算法。

近几年来，研究人员对适用于大擦地角的最优和次优相干检测器进行了研究。Weinberg[45,46]利用KK分布和Pareto分布分析了最优和次优相干检测器的检测性能，发现利用KK分布的检测器设计异常复杂，并不适用于实际雷达系统；而基于Pareto分布的检测器设计则要简单很多。另外，对于Pareto分布杂波环境下的相干探测，可将白化匹配滤波器作为次优检测器使用，具有较高的检测性能。

还有研究针对Pareto分布杂波背景探索了如何实现恒虚警，研究表明，在进行简单的函数转换后即可实现，并可利用简单的解析表达式来关联虚警概率和检测门限。

2017年，Jiang等人[47]在研究基于几何的参数估计方法时，提出了基于有限训练集的正定矩阵空间检测器(PDLT)，验证了其在多目标情况下很稳健，即使在训练样本有限的条件下，PDLT的检测性能依然优于单元平均恒虚警检测器(CA-CFAR)，且不需考虑背景杂波的统计分布模型。WANG等人在此基础上，结合变指数CFAR检测器[48—50]和支持向量机(SVM)[51,52]，提出了基于SVM的智能恒虚警检测器，解决背景杂波类型的自动判断问题。之后，还有研究人员提出了基于正定矩阵杂波功率估计训练SVM的恒虚警检测器(PSVM-CFAR)，该检测器使用滑窗功率估计作为SVM的特征进行训练，并根据SVM分类结果判定参考窗口所处环境，选择合适的自适应检测阈值，实现目标检测。

K分布是对大擦地角海杂波拟合效果较好的分布模型。相比相干积累，相参雷达系统下的非相干积累检测方法可以提高雷达的目标检测速度，达到实时处理的要求。2020年，张坤研究了相参雷达K分布海杂波背景下的非相干积累检测方法的CFAR特性，提出了对杂波功率、杂波非高斯性、杂波散斑协方差矩阵、脉冲积累数和参考单元数CFAR的PWCA-CFAR检测方法和PWCM-CFAR检测方法[53]。在提出的两种非相干积累检测方法中，使用块白化方法对海杂波进行预白化处理，使得杂波散斑协方差矩阵变换为单位阵，并使用了匹配于杂波非高斯性、脉冲积累数和参考单元数的自适应门限，保证了提出方法的CFAR特性。但对大擦地角海杂波中的目标检测效果，依旧有待实际测试。

在海杂波的较弱的信噪比(SIR)背景下检测和跟踪目标，一种方法是使用扫描到扫描(scan-to-scan)处理。Luke等探索了一种新的扫描到扫描框架，用于检测低SIR下的静止目标，并使用30°擦地角下海杂波的蒙特卡洛模拟来分析该方案的性能[54]。该方案通过将反馈因子设置为最小并在大量扫描中积分来达到在最大积分增益下的最佳表现，CFAR处理和二进制积分器通过过滤移动目标和收集可能出现的海峰来降低虚警概率。该方案的缺点是在从二进制积分器进行初始检测之前，需要进行多次扫描。

此外，深度学习和神经网络的发展与应用为目标检测、识别提供了新的优选途径。深度学习的高维特征泛化学习能力，打破了海杂波下目标检测与识别的传统检测方法中需要控制参数、变量进行相互比较的测试壁垒[55]。在参与调试的数据量充足和场景、条件合适的情况下，低擦地角下海杂波中目标检测的算法可以一定程度沿用到大擦地角条件下的目标检测。苏宁远等人[56]将卷积神经网络(CNN)用于海上目标微多普勒的检测和分类。在海面微动目标模型的基础上，在实测海杂波背景中分别构建4种类型微动信号的2维时频图，并作为训练和测试数据集；之后分别采用Le Net,Alex Net和Goog Le Net 3种CNN模型进行二元检测和多种微动类型分类，并进行比较，研究信杂比对检测和分类性能的影响。结果与传统的支持向量机方法进行比较表明，所提方法具有更好的检测和分类性能，能够智能学习微动特征，可为杂波背景下的雷达动目标检测和识别提供新的技术途径。

6 总结与展望

本文对大擦地角下海杂波试验数据集、特性分析、建模和目标检测技术的发展现状进行了梳理总结。着重对大擦地角海杂波研究常用到的Nathanson数据集和Ingara数据集等多个数据集、海杂波模型、大擦地角对海杂波特性的影响以及基于统计模型的目标检测技术研究进展进行了介绍。

已经通过梳理总结发现，雷达工作于大擦地角时，分辨单元内的海面有效散射面积增大，海杂波强度变大，严重影响海面目标检测，尤其是海面微弱目标的检测。现有的海杂波机理研究较为深入，基本理清了大擦地角与小擦地角海杂波差异的物理机制，但特性研究还集中于传统的时域统计和频域谱特性分析，进而形成基于统计模型的目标检测技术，对海杂波的时变非平稳、空间非均匀性考虑还不充分，对大擦地角下探测场景的认知分类还有待于进一步提升。

面向雷达在大擦地角下海杂波特性目标检测的研究前沿和挑战，我们预期以下方面在未来一个时期值得重点关注。

(1)开展试验、获取数据、交流和构建大擦地角数据集。现有的大擦地角下海杂波特性目标检测的相关研究多是在已有的雷达对海数据获取实验中取得，这些实验基本不以大擦地角下为观测的条件因素或在大擦地角下的数据记录太过分散、不全面，使得大擦地角下的对海目标检测数据无法覆盖全测试条件和实际可能发生的条件，在进行建模和特性分析的时候，考虑的因素无法通过数据实验进行好的测试，对适应性更好的新模型和更全面的特性总结有阻碍。公共数据交流环境发展依旧滞后，数据分享和研讨需要更多的进行，共同构建观测角度和影响因素更全面的大擦地角数据集。

(2)基于实测数据的特性分析有待加强。在对大擦地角下的海杂波特性进行分析时，多数研究专注于对其机理层进行推演和总结，对实测数据中产生的特性现象分析和解释程度较浅。多数的实测数据特性分析推导仅仅至可能形成的原因，并未继续用相似条件下或控制可能形成此特性的影响因素后的实测数据进行对比分析总结确认。这一定程度上也与当前大擦地角下实测数据集的不全面、数据量少有一定关系。今后应该继续加强和完善从实测数据特性结果推演形成原因的相关工作，并能最终做到结合特性分析结果对大擦地角下对海目标测试的现象进行机理层面的解释。

(3)验证现有大擦地角下的对海目标检测技术，并发展新的目标检测技术。大擦地角条件下强海杂波对舰船目标检测的影响是一个复杂的问题。今后还需通过大量试验数据对海杂波特性进行多维度研究，对已经提出的目标检测技术加快验证和实际应用周期，并继续发展新的目标检测思路和技术，提升大擦地角条件下雷达目标检测性能。