汇水单元划分尺度对SWMM模型结果的影响

许 迪，严长安，李丽珍，王 辉

(昆明市生态环境科学研究院，云南 昆明 650000)

0 引言

城市暴雨径流机理复杂，影响因素繁多， SWMM模型对各重现期的降雨径流产生过程进行模拟分析合理量化，因此得到广泛运用。在径流污染产汇流特征理论方面，国内学者进行过较深入的研究[1-8]，在SWMM模型中，汇水单元的划分尺度是构建模型的重要步骤。因研究区域范围不同，内部条件不同，划分模型汇水单元的尺度也有所区别。从模型效率方面看，目前的汇水单元划分方式都是以手动划分为主，汇水单元数量越多效率越低；从模型的精度方面看，模型的空间尺度越小精度越高，而小坡度情况下，汇水单元精度越高，径流的路径越复杂，径流总量增加，积水点数量也有变化[14]。从模型的效率和精度两方面考虑，本文以思茅区为例，分别采取：以汇水子片区为主的方式划分汇水单元；以排水户的排口和排水管网进行详细排查和溯源分析，结合道路的方式来划分汇水单元：对这两种划分汇水单元尺度的方式对思茅区模型数据的影响进行分析，为确定建模的空间尺度提供参考。

1 技术与方法

1.1 研究区域概况

思茅区是普洱市的主城区，位于云南省南部、普洱市中南部、澜沧江中下游，地理位置为北纬 22°27′～23°06′、东经100°19′～101°27′。西北沿小黑与景谷县分界，北与宁洱县相连，东南沿曼老江与江城县相连，西南沿澜沧江与澜沧县毗邻，南与西双版纳州景洪市相接，全区总面积约3928km2，辖5镇2乡56个村民委员会15个社区居民委员会。2016年思茅建成区面积20km2，常住人口31.44万人，城市化率72.75%。城区下游设有两座污水处理厂，总处理能力5万m3/d。

本研究以中心城区的截污系统服务范围为研究区域，如图1所示。现场信息调查了解到研究区域为思茅区乃至普洱市人为活动最频繁的地区，人口密度大，产业分布密集，城乡结合带和农村区域均有分布，区域结构复杂，产业化强度大，生活污水和产业化废水量大。在城市污水大负荷压力的作用下，思茅河干流上污水处理厂只有普洱市第一污水处理厂和普洱市第二污水处理厂，污水处理率与削减能力远远无法与产生的污水量相匹配，再加之河道上有大量未并入城市污水管线的排污口，河道污染现象十分严重，特点明显。

图1 研究区域范围图

1.2 研究方法

1.2.1 模型构建

利用研究范围的卫星影像数据，经过GIS解译出六种主要的土地利用类型，即村庄、道路、农田、绿地、裸地及水体，如图2所示。通过GIS的地理面积统计功能，获取各个汇水单元内不同土地利用类型的区域面积[2]，选取对应各土地利用类型的径流系数，详见表1，经过运算得出综合径流系数为0.49，以及各个汇水单元的径流系数。

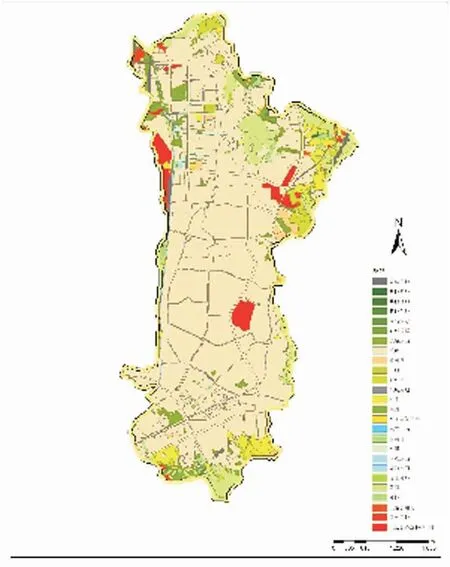
图2 研究区域土地利用类型图

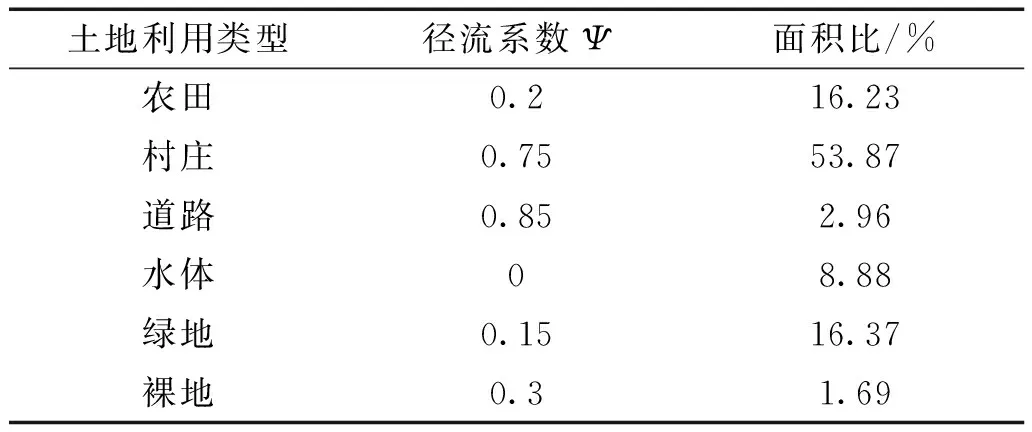
表1 各土地利用类型的径流系数

汇水单元是SWMM模型的基本计算单元，设置汇水单元的面积、宽度、平均地表坡度、不透水面积比、透水地面洼地蓄水量、不透水地面洼地蓄水量、渗透曼宁系数、不渗透曼宁系数、最大下渗速率、最小下渗速率以及衰减常数等诸多参数[3]。选用Horton模型来模拟地表产流过程，此模型的土壤初始下渗能力最大[3]，在降雨条件下对于同一种土壤，其下渗的能力会随着土壤湿度的增加而呈现递减现象，对于不同种类的土壤，其下渗能力的递减规律不同，下渗能力衰减常数一般取值3～6[3]，其他参数通过查阅相关文献选择。根据思茅区现有的雨水管网、节点信息及空间拓扑关系，结合《GB 50014-2006室外排水设计规范》中有关排水管网设计的条例对排水管网进行概化、整理，录入模型中，两个模型均采用一致的管网节点数据、总径流系数、汇水总面积，以及河流、流向、沟渠等相关矢量数据。

考虑到研究区的地形、土地利用情况、管网分布及坡度、易积水点分布等实际情况，确定各汇水单元的平均面积和形状[14]，分别以下述两种方式划分：以汇水子片区为主的方式划分16个汇水单元，即模型A；以排水户的排口和排水管网进行详细排查和溯源分析，结合道路的方式概化整合划分77个汇水单元，即模型B。模型对比图详见图3。通过实测数据来率定参数，参数率定的结果详见表2。

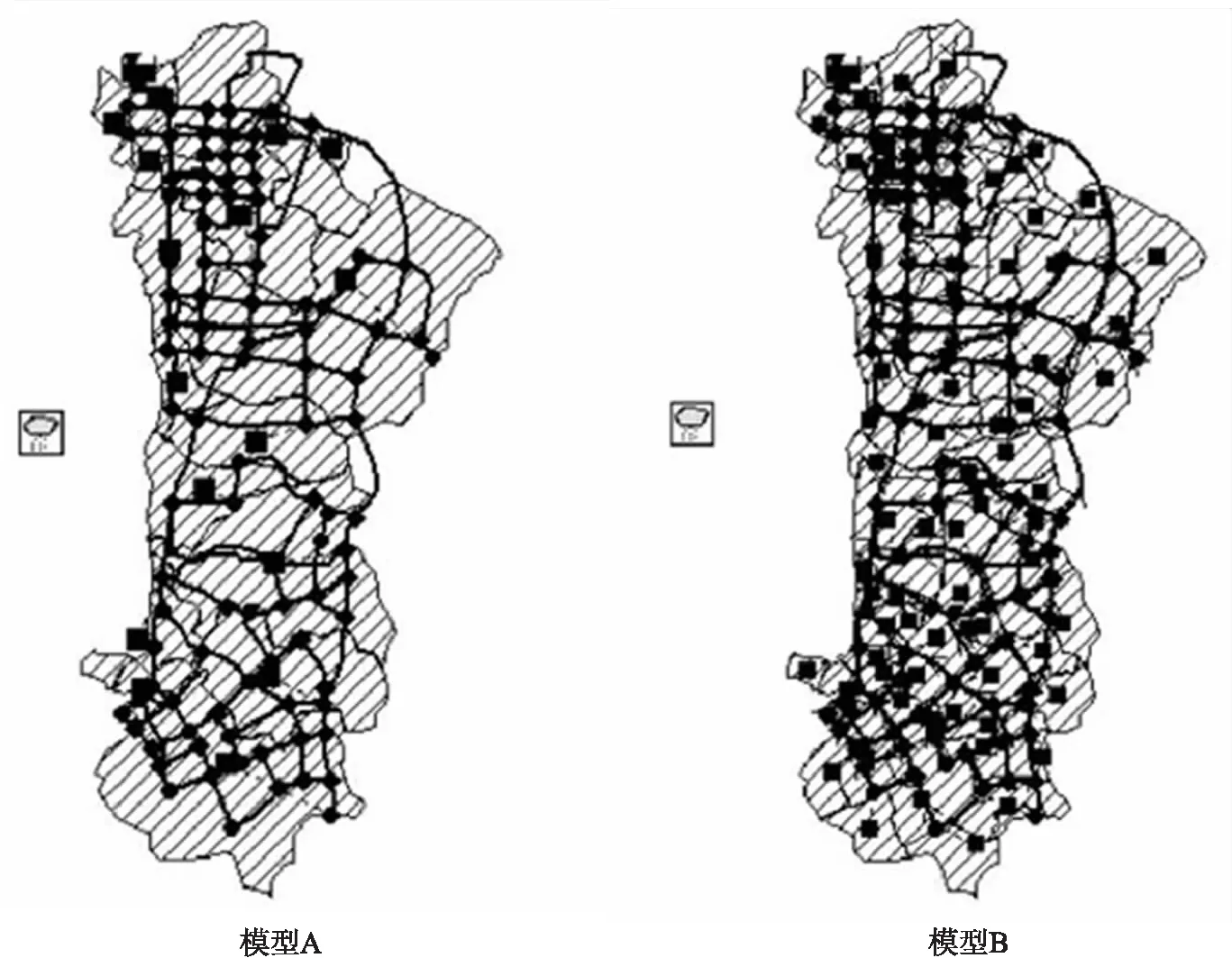
图3 SWMM模型对比图

表2 参数率定结果

1.2.2 降雨设计

降雨设计包括小时降雨量设计和降雨时空变化设计。小时降雨量可以由暴雨强度公式直接推求，降雨的时空变化可用雨型表示[2]。

根据普洱市市场监督管理局发布的《DB 5308/T59—2020思茅区城市暴雨强度公式》，思茅区城市暴雨强度总公式为：

(1)

式中：i—设计暴雨强度(mm/min)；p—重现期(a)；t—降雨历时(min)。

选择历时为60min，重现期0.2a、0.25a、0.5a、1a、2a、3a、5a、10a、20a、30a、50a、100a的降雨进行计算。

采用芝加哥暴雨过程模型模拟降雨过程曲线[2]，结合思茅暴雨强度公式得到：

(2)

(3)

式中：i=(t1)—峰前降雨强度；i=(t2)—峰后降雨强度；a—等于27.42+20.21lgP；b—等于16.905；c—等于0.88；r—雨峰相对位置。

雨峰相对位置r根据思茅降雨站点资料统计，取多场降雨的平均值，如：

(4)

式中：t—峰前历时(min)；T—降雨总历时(min)；m—所统计的降雨场数。

利用以上算法[2]，初步设计了思茅主城范围内1h降雨不同重现期降雨时程分布。由于缺乏思茅主城区的相关资料，参考国内外大量文献资料，大多数研究区域的r值均在0.3～0.5，所以r取0.4，具体降雨时程分布数据见表3和图4。

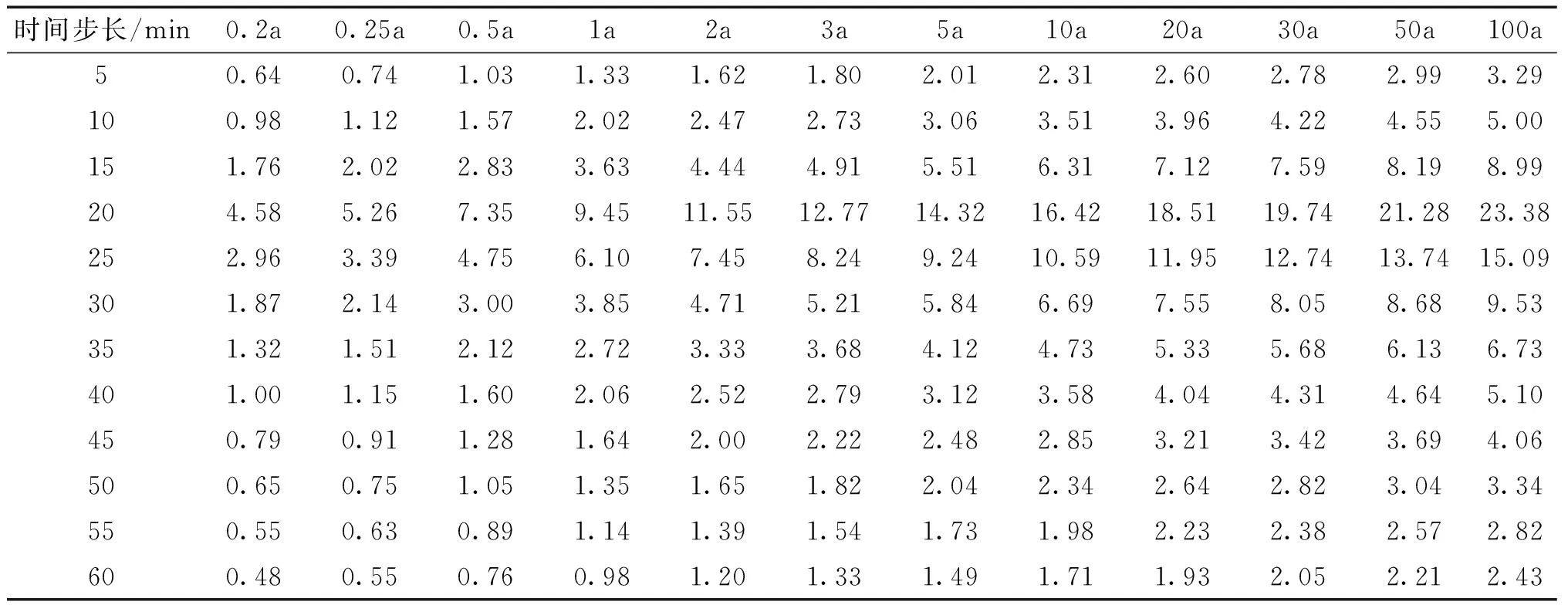
表3 降雨时程分配 (mm/5min)

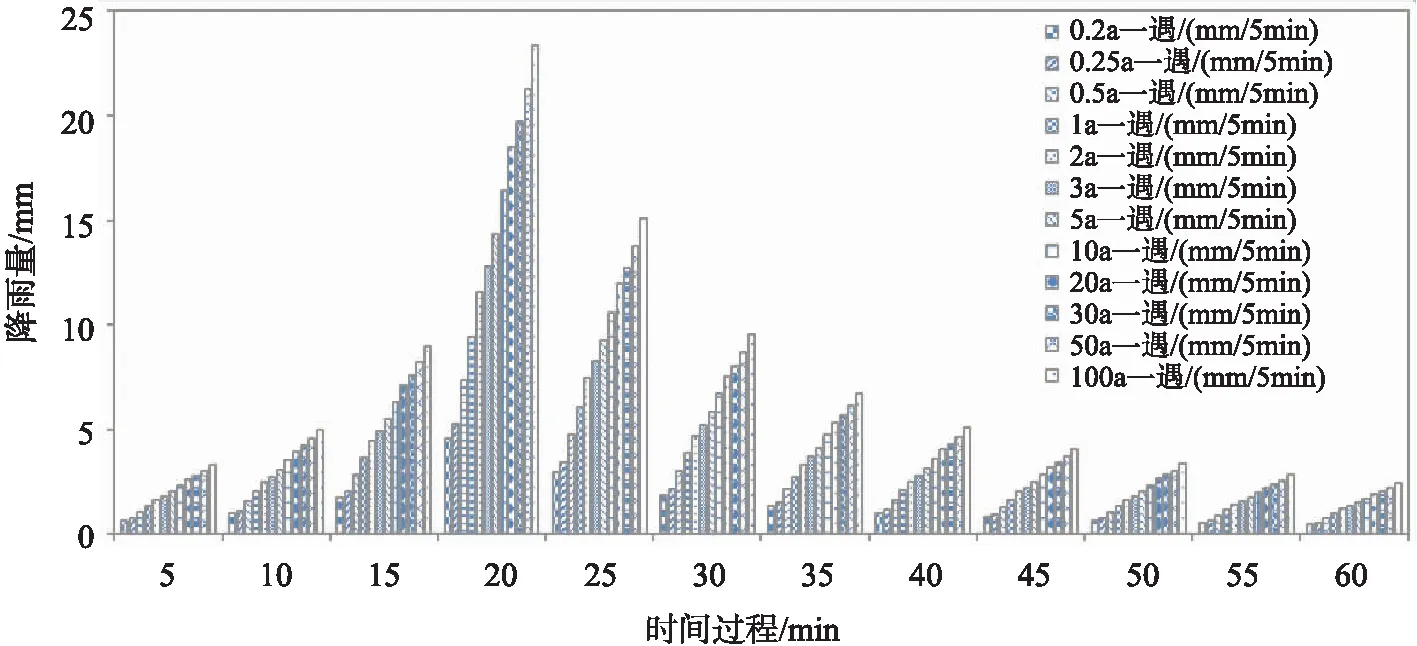
图4 降雨历时时程分配图

2 结果与讨论

两套模型在不同重现期下，总降水量、渗入损失量均一致，而降雨产生的径流和最终地表蓄水量存在很大差异。

模型A地表径流量和最终地表蓄水量随着降雨强度的增加呈现上升趋势，最终地表蓄水量与地表径流的产生量的比值随降雨强度的增加呈递减趋势，两者差距逐渐缩小。降雨强度达到0.2a一遇时，地表蓄水量是地表径流量的5.5倍；降雨强度达到100a一遇时，地表蓄水量是地表径流量的1.6倍。

模型B地表径流量和最终地表蓄水量随着降雨强度的增加呈现上升趋势，最终地表蓄水量与地表径流的产生量的比值随降雨强度的增加呈递减趋势，两者差距逐渐增大。降雨强度达到0.2a一遇时，地表蓄水量是地表径流量的1.25倍；降雨强度达到100a一遇时，地表蓄水量是地表径流量的0.34倍。如图5所示。

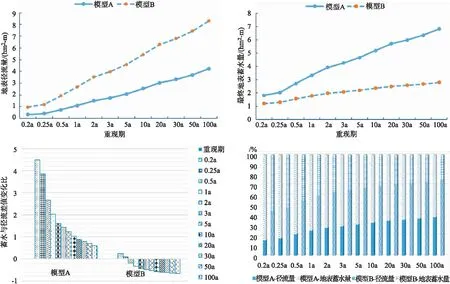
图5 各重现期差异图

随着降雨强度的增加，径流量的升高，系统溢流点位的数量出现较大差异，模型A的溢流点数量没有变化，模型B的溢流点数量由33个增至40个。经计算得知，模型A和模型B的系统收集率均为下降趋势。模型A的系统收集率由0.2a一遇的52.33%降至100a一遇的37.15%；模型B的系统收集率由0.2a一遇的49.66%降至100a一遇的30.29%。模型B的变化幅度更明显，且与实际的系统收集率更为接近。

图6 系统收集率对比图

3 结论

对研究区域划分汇水单元的方式不同，汇水单元的个数也不同，各重现期降雨条件下，随降雨强度的增加，两种方式对结果有明显的影响：

(1)模型B与模型A相比地表径流量和最终地表蓄水量间差值的变化趋势逐步明显；

(2)模型B的系统收集率的变化幅度与实际情况更为接近；

(3)模型B的溢流点数量逐步升高，而模型A的溢流点没有变化。