基于手机信令数据的出行端点识别效果评估

杨 飞，姜海航，姚振兴，刘好德

（1.西南交通大学交通运输与物流学院，四川 成都 611756；2.长安大学公路学院，陕西 西安 710054；3.交通运输部科学研究院城市交通与轨道交通研究中心，北京 100029）

在过去的十年间，手机信令数据已被证明在提取居民交通出行特征上有一定的应用效果.手机信令数据通过记录用户手机发生通话、上网等通信事件时所连接的通信基站的信息，用服务基站的坐标作为用户所在位置的估计，实现对用户轨迹的追踪.其被动式采集的特征使其具有采集成本低和样本覆盖面广等优势.出行端点是交通调查中重要的出行参数，指居民出行的出发点和到达点.利用手机信令数据对用户出行端点的挖掘提取可为日常交通规划和政策制定提供依据，弥补传统居民出行调查的不足，更有望在突发重大公共卫生事件中，及时实现对目标人群出行轨迹的溯源和追踪管控.

早期的手机信令数据定位频率较低，且由于基站密度低使得定位误差也较大.一些研究将用户最高频率访问的基站位置作为出行端点[1-5].随后一些研究通过基于规则的方法对出行端点进行提取[6-9]，即若信令点满足以下两条判别准则即被识别为在出行端点中：1）连续的定位点序列间在空间上的最大距离小于设定的距离阈值；2）该序列中的第一条定位点与最后一条的时间差大于设定的时间阈值.尽管该方法易于实施，但缺乏鲁棒性，结果极易受到异常值的影响[10].随着新一代无线通信技术的发展，蜂窝网络的基站布局密度逐渐提高，互联网经济的迅速发展也带来了信令数据发生频率的提高.因此，手机信令数据的时空解析度得到了极大的改善，在城市市域范围内的定位误差通常可达200 m 以内.通过参考国内外使用GPS 数据和基站定位数据的相关研究[11-14]，有望利用聚类分析算法使得出行端点的识别效果得到进一步提高.

在出行端点识别中，由于通信信号的不稳定，使得即使用户在同一个端点处，其信令定位点也会在多个基站间来回震荡.在算法识别结果中表现为用户在两个或多个出行端点间快速来回出行.当前只有较少的研究针对该问题提出了检测方法，主要分为两种类型：基于模式的方法和基于速度的方法.基于模式的方法搜寻呈现L0-L1-L0-L1或L0-L1-L2-L0（L0、L1、L2为基站编号）的定位点序列作为震荡序列[15-17].然而，该方法容易将实际的往返出行识别为震荡序列.因此，一些研究考虑出行时间信息来优化识别结果[13,18-19].出行轨迹中的高频震荡会呈现用户非正常的高速运动，基于速度的方法通过计算疑似震荡序列的切换速度，如果速度大于设定阈值，则判断它是震荡序列[10].然而，当切换时间间隔非常小时，考虑到位置估计的精确性较低，基于速度测量的方法可能会引起误导[20].结合了两种方法的优势，Wang 等[10]在Wu 等[21]研究的基础上，提出基于时间窗口的方法提取震荡序列.在大多数高频切换的震荡序列处理中，该方法可以取得很好的效果.但是，由于他们以固定时间窗口为单位进行检测（如文献[10]中为5 min），如果震荡序列L0-L1-L0中L1的持续时长较大（超过5 min），将难以被检测出.因此，本文提出端点震荡修正算法，以一个疑似震荡序列作为单位代替固定的时间窗口进行检测，建立了连续的震荡序列的判定准则，较好地解决了以时间窗口为单位的缺陷.

另外，尽管手机信令数据已经被证明在交通调查中的巨大潜力，但已有研究只能从通信运营商处获取居民的信令数据，却无法得知居民真实的出行信息.因此，出行端点识别算法的精度往往难以评估[22-23]，究竟可以在多大程度上相信该项技术的识别结果仍然有待解答.一些研究不得不将信令数据分析结果与其他数据源进行对比.例如，Calabrese等[8]和Alexander 等[12]将手机数据的识别结果与居民出行调查进行对比.然而，居民出行调查等集计统计数据本身也存在一定误差，未必是可靠的参考数据.而且，即使二者在集计统计结果上相匹配，针对每一个个体的推测结果仍然可能有较大误差[23].

本文通过设计实地采集手机信令数据的出行试验，在通信运营商的支持下获取志愿者的手机信令数据，可以从个体角度评估出行端点识别算法的可靠性，是一次新的探索尝试.提出利用凝聚层次聚类算法进行出行端点识别，并在数据预处理和后处理阶段分别提出等时距补点算法和端点震荡修正算法对识别结果进一步优化.最后将手机信令数据的识别结果与出行日志记录的真实数据进行对比评估，从出行者个体和集计角度分析了提出算法的有效性.

1 数据采集试验

1.1 出行试验设计

本文使用的手机信令数据来源于中国联通.该运营商不仅提供了超过一百万用户一个月的匿名化手机信令数据，还可以提供本文出行试验中志愿者的实名信令数据.其中，志愿者的信令数据均经过本人实名认证同意后提取，因此可以获取其手机号码等个人信息.

在以往研究中，由于手机信令大数据中真实出行信息的缺乏，提出算法的可靠性一直难以准确评估.在运营商的支持下，本文获得非常难得的机会，可以在采集信令数据的同时得知出行者真实的出行信息.

出行试验设计安排在中国某市.该市拥有超过480 万人口，是具有高人口密度和复杂交通环境的典型城市地区，市域范围内联通基站超过1.9 万个，基站的平均覆盖半径小于150 m.

设计了3 种不同的出行目的：工作、居家和娱乐购物.不同出行端点间的交通方式包括5 种常用的方式：小汽车、公交车、地铁、自行车和步行.志愿者被要求在出行过程中随身携带安装中国联通SIM卡的智能手机用于手机信令数据采集.同时，在智能手机中安装用于GPS 轨迹数据采集的APP.该APP在出行试验中持续运行，GPS 轨迹数据的采样频率为每秒一次，可以记录志愿者较为准确的位置信息.另外，在出行试验中要求同步记录出行日志，记录包括每个出行端点的到达和离开时刻，交通方式换乘时刻，交通拥堵时间等等.GPS 轨迹数据和出行日志数据可作为后续进行算法评估对比的真实数据.2019 年9 月8 日—12 月21 日，由15 位志愿者陆续进行超过400 次出行，采集了以工作为出行目的的端点141 个，以居家为出行目的的端点187 个，以娱乐购物为出行目的的端点85 个，共采集了超过1080 万条GPS 轨迹记录.运营商根据志愿者SIM卡信息，提供了试验期间超过17.9 万条手机信令轨迹记录.

1.2 数据分析

采集的手机信令数据不仅包含主动通信事件，如通话、短信和上网等，也包含被动通信事件，如位置更新、周期性位置更新和切换等.数据样例如表1 所示.表中的经纬度反映了当前通信事件中服务基站的坐标，即用服务基站坐标表示用户所在位置，这也是基于信令数据定位的基本特征.

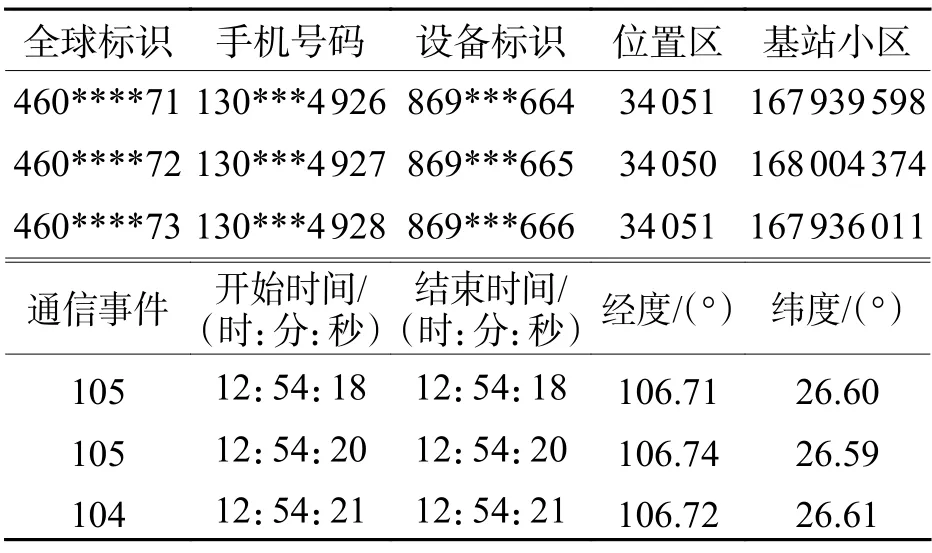
表1 手机信令数据样例数据Tab.1 Example records of cellular signaling dataset

分别统计用户出行端点处和出行过程中的相邻信令数据的时间间隔分布，如图1 所示.可以看出，1 s 的数据间隔发生概率最大，且随着间隔值的增加发生概率迅速下降.然而，时间间隔值3241 s 和3600 s 的发生概率陡然增加.这是由于信令数据中周期性位置更新的发生周期为3241 s 和3600 s，即手机会周期性地与周边服务基站发生交互而留下的信令记录.另外，出行端点处信令发生时间间隔的累积概率分布比出行过程中上升更快，这是因为用户通常在出行端点处更加频繁地使用手机，信令数据发生更加频繁.出行端点处和出行过程中手机信令数据发生时间间隔的中值分别为31 s 和107 s.

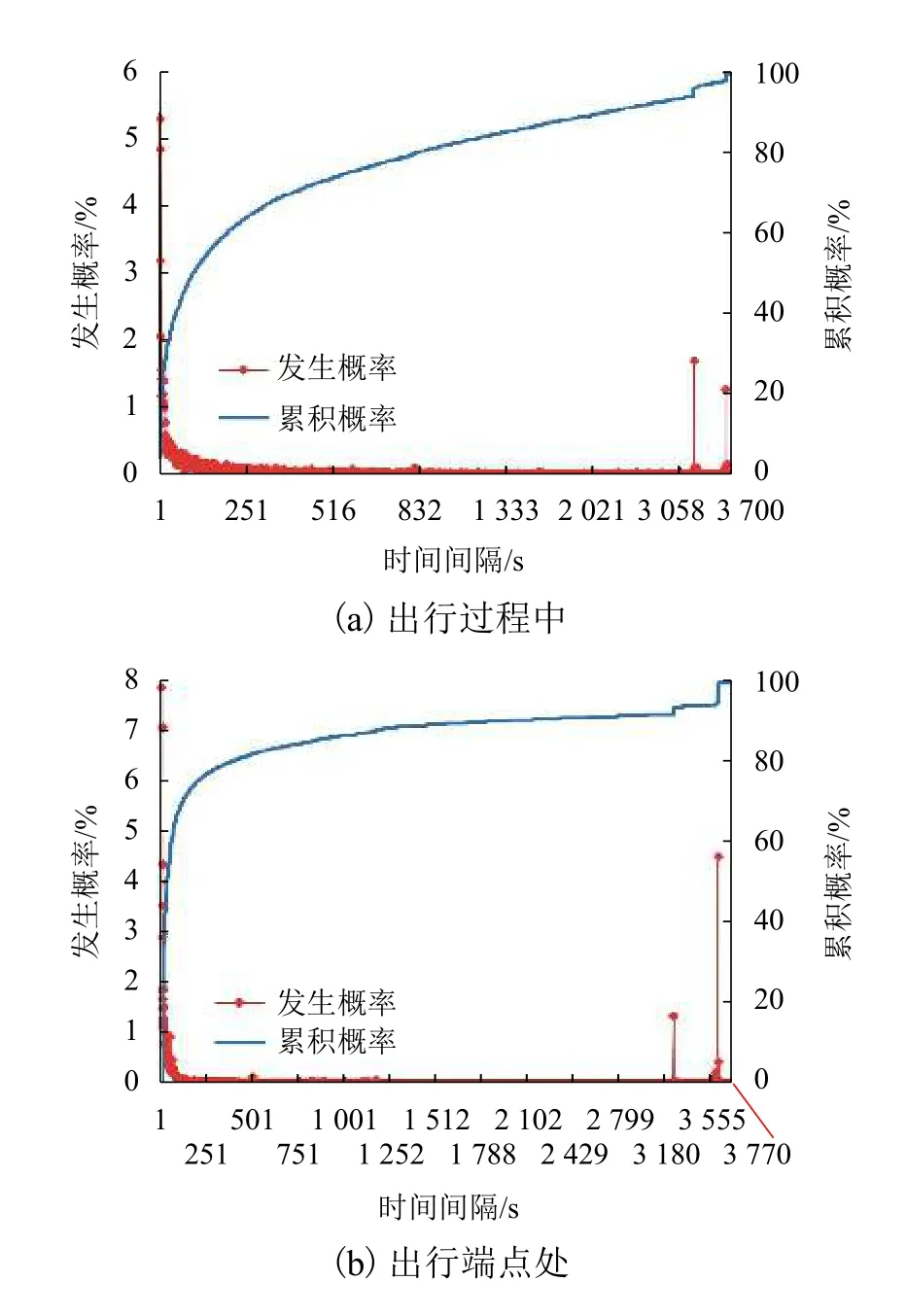
图1 相邻手机信令数据的时间间隔分布Fig.1 Time-interval distribution of adjacent cellular phone records

分析对比手机信令数据和GPS 轨迹数据在空间上的定位分布，如图2 所示.图2（a）为某用户一天出行的GPS 轨迹数据在地图上的空间分布.由于GPS 数据采集软件的采样频率为每秒一次，因此定位点分布非常密集，能够高频率且较为准确地反映用户的位置和出行轨迹.图中黄色的圈和其编号分别表示该用户该天出行端点的位置和顺序.编号 ①和 ⑨ 表示同一个出行端点位置，即用户的家.图2（b）为该用户该天的信令数据空间分布，也反映其使用基站的位置.与GPS 轨迹数据相比，信令数据定位点在地图上的分布相对稀疏.这是因为只要用户在同一个基站的服务范围内，他的信令定位位置都由该基站的坐标表示.因此手机信令数据的定位精度较大程度受到基站分布密度的影响.尽管如此，信令定位坐标仍然能够大致反映用户的出行轨迹.

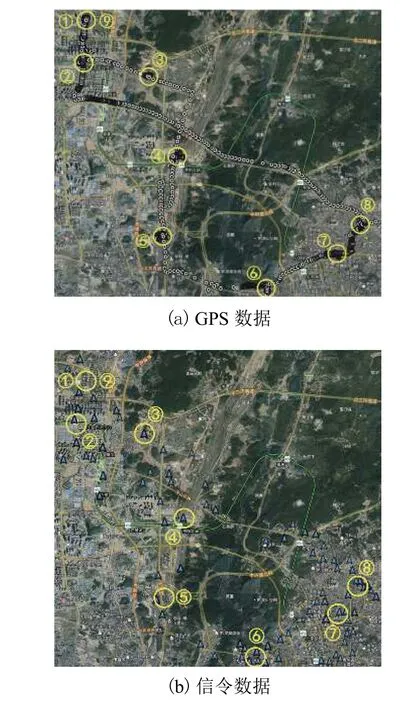
图2 某用户一天出行的GPS 数据和信令数据在地图上轨迹分布Fig.2 User’s all-day traces in GPS data and cellular signaling data on map

2 出行端点识别算法

2.1 等时距补点算法

手机信令数据的数据间隔是不均匀的，这意味着不同点位在时间上的权重不同.如图3 所示，信令定位点A和点B都在出行端点上，这意味着点A不仅仅代表其自身位置，也代表个体在t1时间段内都在该出行端点处.由于在出行过程中，个体的位置点C和点D时刻在变化，它们只能代表某一个时刻的位置.若定位点每秒出现一次，点A处的定位点显然会更加密集，所以点A在时间上的权重更大.可是信令数据的发生间隔并不稳定，且后续的聚类算法会忽视轨迹点的时间权重，这会导致以点A为代表的出行端点被忽视.因此，本文采用等时距补点算法，以已有信令数据定位坐标为基准，对每秒的个体所在位置进行估算，平衡定位点间时间权重的差异.

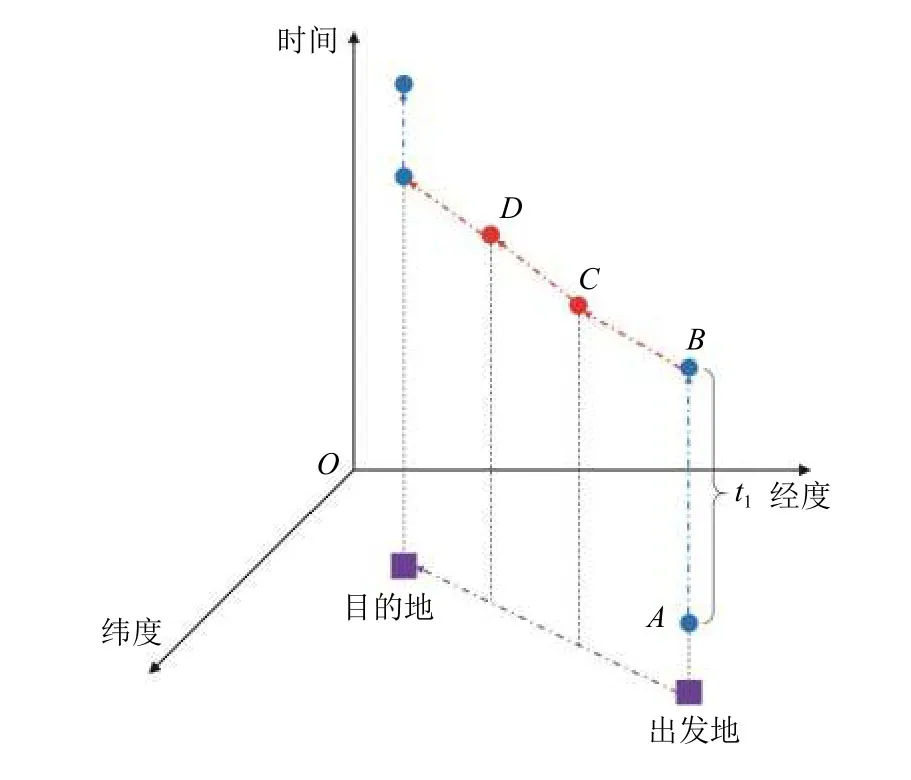
图3 定位点时间权重示意Fig.3 Time weight Diagram of traces

算法表述如下：

定义信令数据点时空三维坐标为 (x,y,t)，分别为经度、纬度和时间.已知相邻信令点坐标分别为(x1,y1,t1) 和 (x2,y2,t2)，根据式（1）计算得 [t1,t2]区间内任一时刻tn的坐标值 (xn,yn).

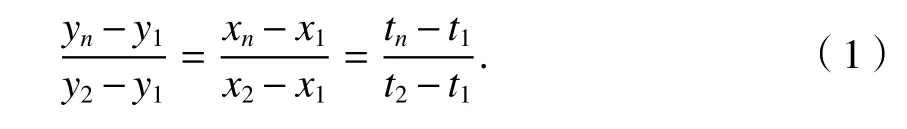
以1 s 为间隔在信令点间进行补点插值.由于后续的聚类算法需要迭代计算每两点间的距离，对计算机算力有较大的要求.在算力不足的情况下，可以适量增加插值周期TF.方法为：在1 s 间隔补点的基础上，重新每隔TF选择一个定位点，并删除中间未选中的.TF的增加会给后续出行时间相关信息的识别带来更多的误差，因此本文建议TF不应大于60 s.

信令数据补点前后的时空分布如图4 所示.补点后可以更直观地看出用户全天的出行轨迹.尽管定位点与实际的用户位置之间存在距离误差，但补点后更有利于出行端点的提取.等时距补点能够使得定位点间的时间间隔相同（均为TF）.因此，某处定位点的个数也代表了停留时间，极大地增加了用户在出行端点处定位点的密度.

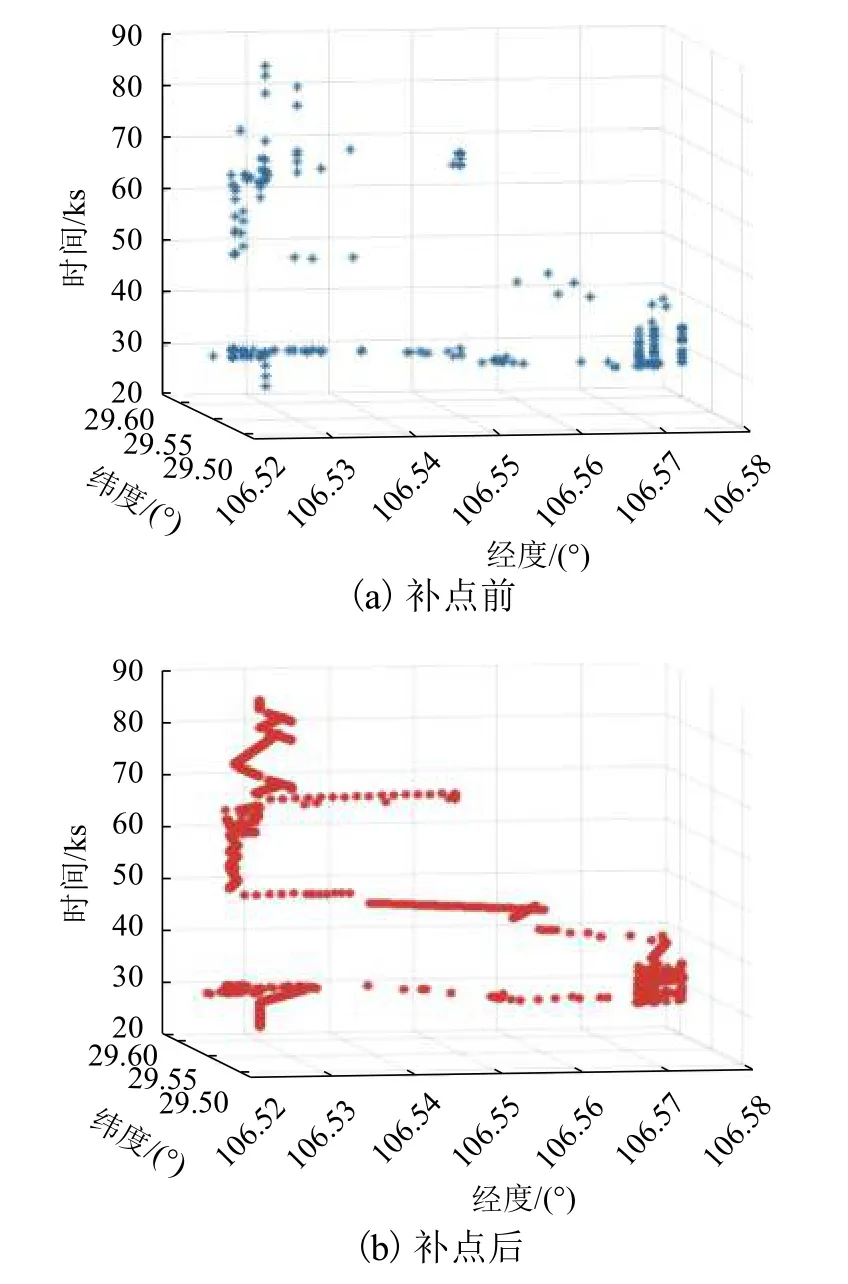
图4 某用户一天定位点时空分布Fig.4 Space-time distribution of user’s all day traces

2.2 凝聚层次聚类算法

常用的K均值聚类算法需要提前确定聚类个数，即出行端点个数，这显然难以提前得知.凝聚层次聚类算法的待确定参数是聚类半径，该半径值也具有现实意义，即用户在出行端点处的服务基站与用户真实坐标之间的距离.因此，在本文中更具有适用性.

凝聚层次聚类算法递归地对定位点进行合并，直到满足某种终止条件为止.其聚类原则与增量聚类类似，但初始定位点选择距离最近的两点，而不是随机的[10-11,14].

假定有N个定位点待聚类，包含任意两点间距离的距离矩阵D大小为N×N.类簇编号用 (i)表示，d[(r)，(s)]表示簇 (r)和簇(s)之间的距离，也是D中第r行和第s列的元素，s∈i,r∈i.L(j)表示第j次聚类的层次.算法步骤简单描述如下：

步骤1L(0)=0，j=0.将每一个定位点视为一个类簇；

步骤2从所有现存类簇中，根据min (d[(r)，(s)])找到距离最近的类簇(r)和(s)；

步骤3令j=j+1，L(j)=d[(r)，(s)]，然后删除类簇 (r)和 (s)，并将它们合并为新的类簇 (r，s)；

步骤4更新距离矩阵D，即删除关于类簇(r)和(s)的行列，并增加新生成的类簇(r,s)和其他类簇之间的距离；

步骤5重复步骤2 至步骤4，直到所有类簇之间的距离都大于待确定的聚类距离阈值R.

类簇之间距离为

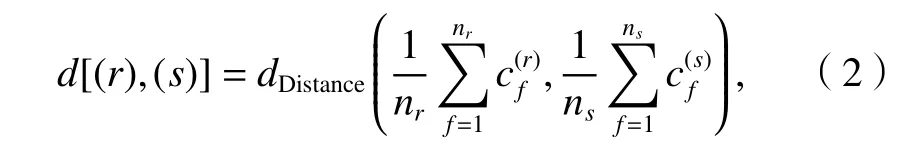
式中：ni为第i类簇包含定位点个数；为第i类簇中第f个定位点；dDistance(•)为计算不同坐标（经纬度）间距离的函数.

最终，所有的定位点被聚类成不同的类簇.

2.3 端点震荡修正算法

由于通信信号在传播过程中易受到地形、天气等多种因素的影响，在同一位置基站信号强度会不断变化，导致即使个体在位置固定的出行端点，也可能和周边多个基站发生交互.在出行端点识别中，如果用户所处位置周边基站较为稀疏，来回切换的服务基站间距离过大，聚类算法中适应于市区的距离阈值R此时可能偏小，易把同一出行端点识别为多个，如图5 所示.图中：Dp为待确定的震荡距离阈值；为簇b的持续时间；Tp为待确定的震荡时间阈值；为疑似震荡编号序列，I为定位点聚类后连续不同的类簇数编号；z为连续震荡序列数；蓝色簇a和紫色簇b实际在同一个出行端点，但在聚类算法结果中表现为用户在簇a和簇b间来回移动.本文定义这种现象为端点震荡，需设计端点震荡修正算法使得簇a和簇b合并为一个类簇.

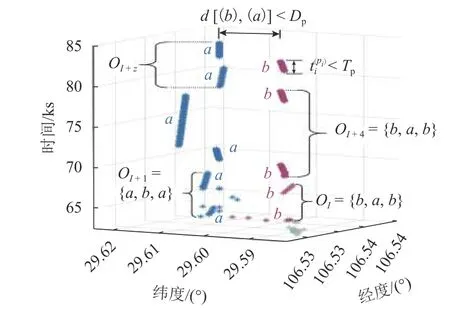
图5 端点震荡修正算法示意Fig.5 Schematic of location oscillation correction method

然而，图5 中存在一个特殊的案例.OI+4中的类簇（a）持续时长较长，导致，即不能满足时间阈值要求.因此，需要添加一条新的判定准则：因为OI+4中所有的类簇（簇（a）和簇（b））都已在之前的OI∪OI+1∪···∪OI+z里确定为在端点震荡序列中，所以OI+4仍然被判断为端点震荡序列.而在Wang等[10]提出的以固定时间窗口作为检测单位的方法无法解决该问题.最后，图5 中的端点震荡序列均被归为簇（a）.

5）循环终止条件

步骤7更新M和M'，转到步骤2 搜寻OI+z后的疑似震荡序列，直到M'中的最后一个元素.最终，统计每一个类簇的持续时长.如果类簇的时长大于待确定的停留时间阈值Tu，则类簇被判定为一个出行端点簇，其中，v为满足停留时间阈值的类簇编号.出行端点的坐标为

3 结果验证与分析

3.1 参数选取

考虑到算力等因素的限制，选取等时距补点插值周期F=10 s.4G 用户的原始信令数据平均约1700 条/(人•天)，经过周期F的补点后达到约8600 条/(人•天)，在本文的硬件设施条件下每人每天的出行端点识别算法的程序计算时长为9 s 左右，能够较好地兼顾算法的运行效率和精度要求.

停留时间阈值Tu不应该小于用户在活动点的停留时长，但是设置过小可能会导致出行途中的短时间停留被识别为出行端点.基于已有研究并经过重复测试，设置Tu为10 min[12-13].

在出行端点识别结果中，主要存在以下几种错误识别情形：1）合并识别，将多个实际出行端点误识别为1 个出行端点簇；2）分段识别，将实际中1 个出行端点误识别为多个出行端点簇；3）未识别，实际中某个出行端点处产生定位点均未被识别为出行端点簇；4）额外识别，将实际中非出行端点处产生的定位点误识别为出行端点簇.本文利用正确率（Acc）和多识别率（Mu）两个指标对以上错误识别进行评价，如式（3）、（4）.

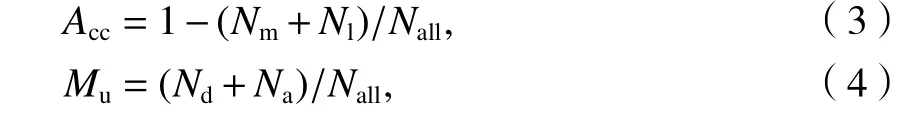
式中：Nm为合并识别个数；Nd为分段识别个数；Nl为未识别个数；Na为额外识别个数；Nall为总出行端点个数.

对不同的距离阈值R进行重复试验测试，结果如图6 所示.可以看出，随着R取值的增加，端点识别正确率逐渐降低，这是由于R值越大越容易导致合并识别个数的增加.而由于出行端点处信令数据的高度集聚性，较小的R值已经能够使得未识别个数处于较低水平，未识别个数对R值增加的敏感性非常有限.同时，多识别率呈现先减小后增加的趋势，这是由于R值较小时易产生分段识别，而过大时易导致额外识别（如交通拥堵导致较长时间停留）.综合来看，当R=400 m 时，多识别率达到最低而正确率仍位于较高水平，尽管正确率下降0.6%，但多识别率下降3.3%，整体识别效果相对最好.另外，端点震荡修正算法中的震荡时间阈值Tp和震荡距离阈值Dp分别设为30 min 和800 m，可以达到较好的识别结果.

图6 不同距离阈值下出行端点识别效果Fig.6 Activity location recognition results using different distance thresholds

3.2 案例分析

为了验证提出的出行端点识别算法的有效性，以某用户一天的定位数据为例对识别结果进行论述，如图7 所示.图7 为该用户定位点（补点后）的时空分布以及识别结果的时空三维视图.图中不同颜色的定位点表示它们属于不同的类簇.其中，持续时长超过停留时间阈值Tk的类簇被确定为出行端点簇.可以看出，该用户该天进行了3 次出行，有4 个出行端点，即图中红色框标注.其中，出行端点 ④ 即是图5 中经过震荡修正的结果.由于端点 ①、④ 在同一个出行端点位置，即用户的家，因此有两个识别端点坐标.4 个出行端点的距离识别误差都在160 m以内.通过将识别出的出行端点簇的到达时刻和离开时刻与出行日志进行比较，时间误差均在5 min以内.

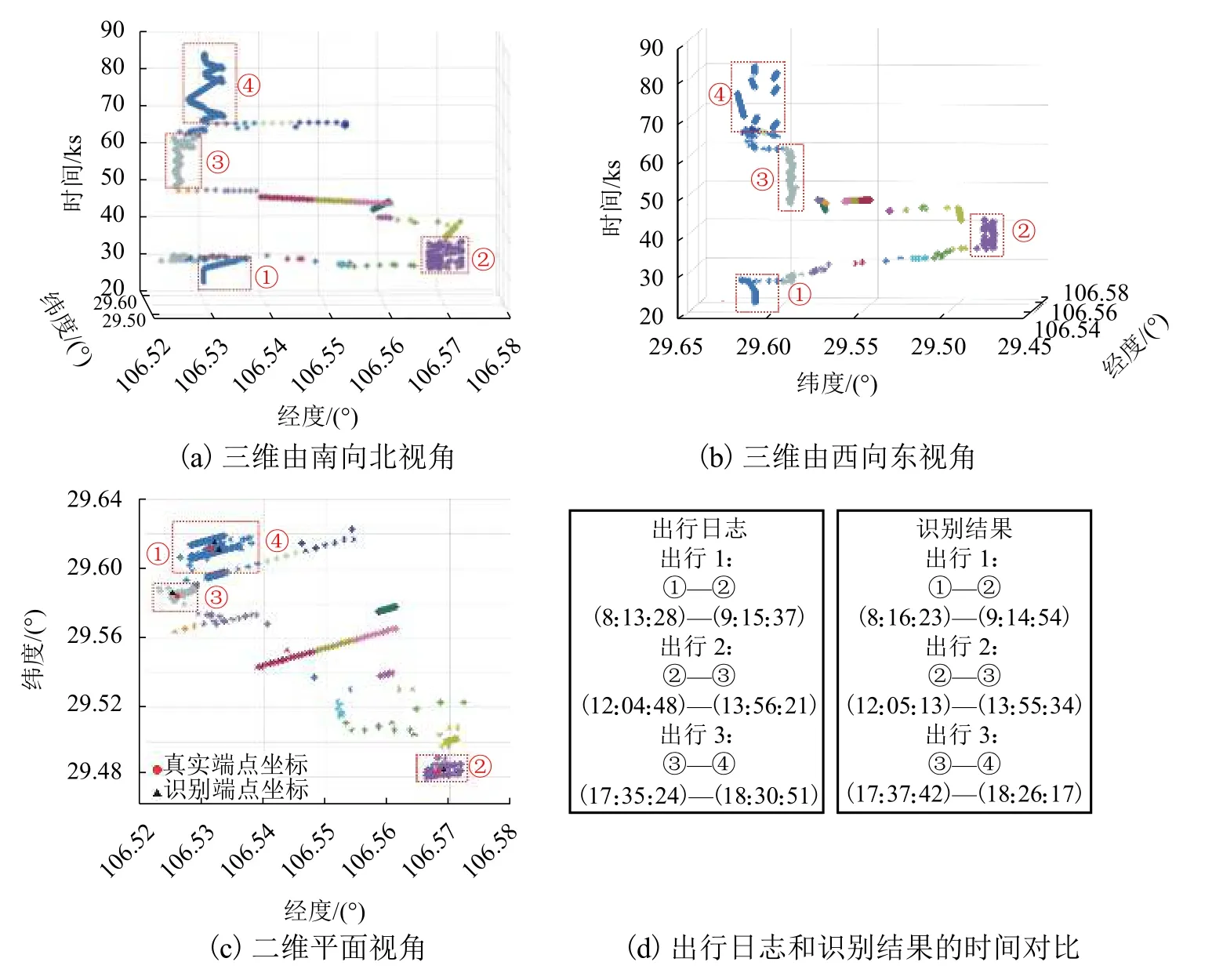
图7 某用户出行端点识别结果样例Fig.7 Case study result of user’s activity location recognition

3.3 结果分析

为评估出行端点的整体识别效果，使用两个比例指标：正确率和多识别率，来评估端点数识别效果.同时，使用3 个平均误差指标：到达时间误差、离开时间误差和距离误差，来评估出行时间和端点位置的识别效果.其中，到达/离开时间误差等于正确识别的出行端点簇的起始/终止时刻与实际在出行端点到达/离开时刻之间差值的绝对值；距离误差等于个体实际出行端点坐标与识别端点坐标之间的距离.

表2 为不同出行目的的出行端点识别比例、时间误差和距离误差的统计结果.整体识别正确率为84.1%，多识别率为2.3%.在出行时间识别中，到达时间误差和离开时间误差分别为5.3 min 和7.7 min.在3 种出行目的中，离开时间误差均比到达时间误差大2～3 min.这主要是因为出行者乘坐公交或打车时，他们的路边等待位置通常与其出行端点之间距离很近，即小于聚类距离阈值R，导致此时他们仍然被识别为在出行端点中，直到他们上车驶离才会被识别为离开该出行端点.因此，路边候车时间使得离开时间的识别误差增大.另外，出行端点坐标识别的平均距离误差为219.6 m，而常用的四阶段模型中交通小区的规模通常大于 500 m×500 m.识别误差小于该规模，因此该结果可以为当前的交通需求预测模型提供参考.

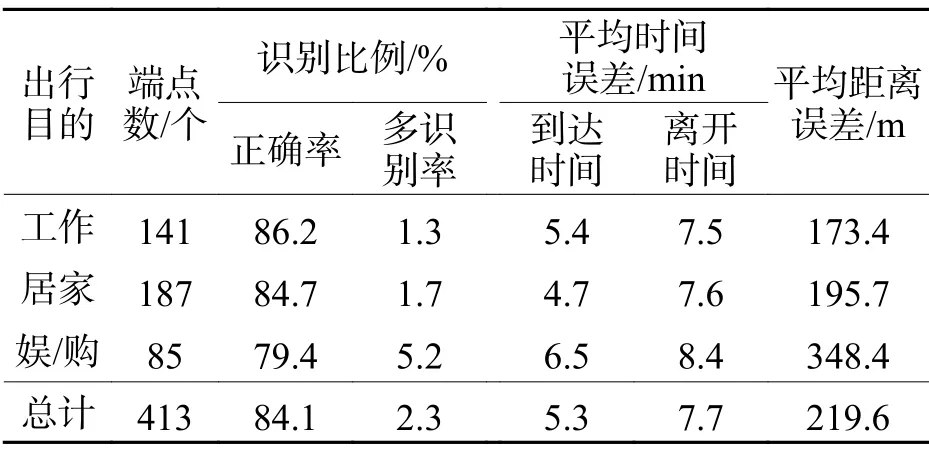
表2 出行端点识别统计结果Tab.2 Recognition results of activity locations

通过比较不同出行目的的识别结果，可以看出：算法在“工作”目的的端点中识别效果最好.这主要是因为用户在工作期间活动范围很小，且工作地点通常在有着较高基站密度的市中心地区.作为对比，“娱乐购物”目的的出行端点识别效果最差.这主要因为用户在购物商场、公园等地区的活动范围较广，易导致其服务基站不断变化，所以信令定位点在空间上分布更广，聚类效果也更差.尽管如此，平均时间识别误差在9 min 以内，距离识别误差在350 m 以内，即小于交通小区范围，仍可为居民出行调查提供参考.

4 结 论

1）相比于已有的以固定时间窗口为检测单位的震荡修正方法，本文提出的以疑似震荡序列为检测单位的方法可以取得更好的效果.

2）出行端点的识别准确率为84.1%，到达和离开时间识别误差在7.7 min 以内.但由于路边候车的影响，离开时间的识别误差相比于到达时间识别误差较大.

3）“工作”和“居家”目的的端点识别效果较好，可结合全市域手机信令数据，对城市居民职住情况做进一步统计分析.“娱乐购物”目的的识别效果相对较差，可考虑结合地理信息系统数据和城市POI 数据等对识别结果做进一步修正优化.

4）通信基站的分布特征，尤其是基站密度会对出行端点识别产生较大影响，未来将进一步开展不同通信场景下手机信令数据采集的实地同步对比试验，同时结合通信仿真等技术手段，对不同通信参数场景下的技术敏感性做深入分析.