“三单”协同,让学习过程真实而完整
沈凤飞 许茹暖


摘要:“真学课堂”的学习单,是集课前预习单、课中研学单、课后练习单为一体的课堂导学单。预习单让学生学有所备,研学单让学生学有所悟,练习单让学生学有所得。“三单”协同,帮助学生解构旧知、理解新知、重构认知、巩固拓展、迁移应用,经历真实而完整的学习过程。
关键词:“真学课堂”;学习过程;预习单;研学单;练习单
新课改以来,越来越多可以体现学生主体地位的学习方法被运用于课堂教学中,学习单也应运而生。“真学课堂”的学习单,是集课前预习单、课中研学单、课后练习单为一体的课堂导学单,帮助学生解构旧知、理解新知、重构认知、巩固拓展、迁移应用,经历真实而完整的学习过程。本文以苏教版小学数学六年级上册《比的基本性质及应用》一课为例,呈现“三单”协同下的“真学课堂”。
一、预习单,让学生学有所备
学习是一种有准备的活动。这个“有准备”,不仅指知识的准备,也指情感和意愿的准备。预习单的设计就是基于这样的理念。一方面,通过预习单激活学生已有的与所学内容相关的知识,让学生带着这些储备知识走向学习,让新旧知识产生联系;另一方面,唤起学生学习的欲望,为新知识的学习做好情感的准备。
(一)激活旧知
很多时候,学生不能自主解决问题,就是因为没有让知识结构化,在面对新知的时候,无法及时调用与之有联系的旧知。预习单的使用,能够很好地解决这一问题。教师在设计预习单的时候,要注重知识点的前后联系,将与本课相关的旧知纳入预习单中,有效地帮助学生实现知识结构化。比如,《比的基本性质及应用》一课,与“比的基本性质”相关的知识点有“求比值”“商不变的规律”“分数的基本性质”等,据此,预习单中设计了如下两个问题来激活旧知:
1.写出得數,看看每一组算式之间有什么联系。
(1)40÷8=20÷4=
(2)24÷4= 2.4÷0.4=
(3)120÷20= 12÷2=
被除数和除数()乘或除以()的数(0除外),商不变。这叫作商不变的性质。
2.填一填。
416=8()=()48=10()=()20
分数的分子和分母()乘或除以()的数(0除外),分数的大小不变。这叫作分数的基本性质。
(二)联结新知
对新知的挑战是唤醒学生学习动机的“良药”。预习单还需要唤醒学生学习新知识的情感与意愿,激发学生的学习动机。学生能够自己解决的新知问题,可以激发学习期待;而不能自己解决的新知问题,则成为学习需要。因此,《比的基本性质及应用》一课的预习单,还设计了这样一个新知问题:
3.求比值,观察得数,你发现了什么?
3∶4= 6∶8= 9∶12= 15∶20=
比的前项和后项()乘或除以()的数(0除外),比的大小不变。这叫作比的基本性质。
二、研学单,让学生学有所悟
预习单是“唤醒”与“联结”,研学单则是“留痕”与“展示”。“留痕”是指提供一个清单式学习支架,让学生根据一个个任务开展学习,将学习的过程清晰地留在研学单上;“展示”是指开展交流和评价活动,以促进学生更好地学习。
(一)以任务为支架
研学单基于预习单,根据学习目标,给学生提供具体清晰的课堂学习任务。学习任务可以是一个核心任务,也可以是几个环环相扣的关联性任务。比如,《比的基本性质及应用》一课的学习目标是:(1)能用语言或文字表示比的基本性质;(2)能应用比的基本性质化简比;(3)能说出化简比与求比值之间的联系和区别。因此,该课的研学单上就设计了这样两个任务:
任务一:比的基本性质
求出下面每个比的比值,并把比值相等的比填入等式。
4∶516∶2032∶4040∶50
()∶()=()∶()=()∶()=()∶()
观察等式,联系分数的基本性质,你认为比具有怎样的性质?(提示:比的前项能不能是0?比的后项能不能是0?)
任务二:比的基本性质的应用——化简比
像4∶5这样,前项和后项只有公因数1的比,我们称为最简单的整数比。
试一试:把下面各比化成最简单的整数比。
(1)12∶18=(12÷6)∶(18÷6)
=( )∶( )
想一想:为什么要同时除以6?
(2)56∶34=56×12∶34×12
=( )∶( )
想一想:为什么要同时乘12?
(3)1.8∶0.09=(1.8×100)∶(0.09×100)
=( )∶( )
=( )∶( )
想一想:为什么要同时乘100?
学生根据研学单一步步地开展学习,而且,他们的学习过程清晰地留在了研学单上,因此也成了教师教学的线索单。
(二)以评价为支持
研学单的学习,是一种自主学习,因此,评价显得尤为重要。在整个学习过程中,教师成为一名评价者,以评价引导和督促学生的学习过程。同时,研学单对每一个学习任务都设计了清晰的评价标准,让学生也能参与到评价中来,真正经历整个学习过程。设计评价标准需要注意三点:一是评价要与目标对应。不对应目标的评价是没有意义的,也无法判断学生是否达成了目标。二是学生要看得懂评价标准。要用浅显易懂的语言进行表述,让学生一看就懂。三是学习任务要可评可测。比如,《比的基本性质及应用》一课中,任务一的评价标准有两条:(1)能正确填空;(2)能用自己的语言或文字表述出比的基本性质。任务二的评价标准有三条:(1)能独立尝试化简比;(2)能正确地化简比;(3)能用自己的语言和同伴说说为什么要这样化简。
研学单在整节课中是一个重点,有助于学生在任务驱动下全程参与学习过程。
三、练习单,让学生学有所得
基于“唤醒”与“联结”,有了“留痕”与“展示”,接下来的练习单就是“巩固”“检测”与“拓展”。围绕课堂学习的重点设计练习,意在巩固学习的成果,检测学习的效果及学习的迁移和运用情况。
(一)新知的巩固
知识巩固作为练习单的功能之一,需要教师结合研学单的实施情况,即课堂教学的实际情况,立足学生学习过程中的薄弱和不足之处,设计相应的练习。比如,《比的基本性质及应用》的练习单中设计了这样的巩固练习题:
1.填空。
(1)比的基本性质是:( )。
(2)5∶8的前项乘3,要使得比值不变,后项应乘()。
(3)3∶4的后项加上12,要使比值不变,前项应加上()。
2.化简下面各比,并求出比值。
4.2∶47120∶7217∶14910268
设计这两个巩固练习题,是因为从课堂中发现学生存在两个问题:一是化简比的正确率不高;二是混淆化简比和求比值。
(二)新知的检测
练习单要指向研学单中预设的学习目标和学习任务,其对新知学习的检测才是真实有效的。比如,《比的基本性质及应用》一课,上述两道练习题,第1题对应第一个学习目标“能用语言或文字表示比的基本性质”,第2题对应第二、第三个学习目标“能应用比的基本性质化简比”“能说出化简比与求比值之间的联系和区别”。如此,可以较为真实地检测出学生课堂学习的效果。
(三)新知的拓展
练习单除了巩固、检测之外,还承担着拓展的责任:拓宽思路,发散思维,更加全面深入地理解新知,提高运用能力。比如,《比的基本性质及应用》一课练习单的第3—4题,就是拓展练习题:
3.把下面各比改写成后项是100的比。
(1)发芽种子数和试验种子数的比是18∶25。()
(2)新光电视机厂九月份完成的产量与计划产量的比是214∶200。()
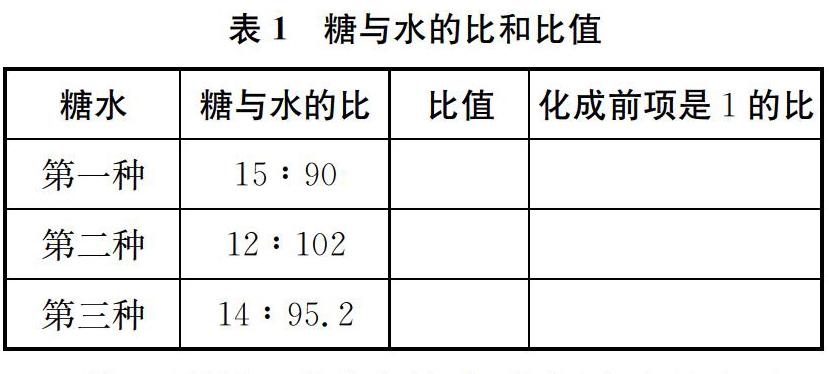
4.下面是几种糖水中糖与水的比,完成表1,再比一比哪种糖水更甜,说说你的理由。
糖水糖与水的比比值化成前项是1的比第一种15∶90第二种12∶102第三种14∶95.2第3题是“比的基本性质”的应用,也是为后面学习百分数知识做铺垫;第4题则是“比”与“比值”的生活运用,将数学与生活紧密联系起来。
综上可见,预习单让学生带着知识、经验和积极的学习情感进入学习;研学单通过任务设计,让学生成为学习活动的主人,在活动中获得知识和技能;练习单围绕学习主题,拓展延伸,迁移应用。“三单”作为课堂学习支架,相互协同,让学习过程真实而完整。
参考文献:
[1] 高国栋.如何在小学数学教学中培养学生的自主学习能力[J].新课程,2020(8).
[2] 朱怡虹.活动“有形”,建构“無声”——用“设计”成就儿童深度学习的几点思考[J].小学教学研究, 2018(34).

